Đánh giá đặc trưng phát hiện của bộ phát hiện tương phản tín hiệu trên nền nhiễu bất định thông tin tiên nghiệm

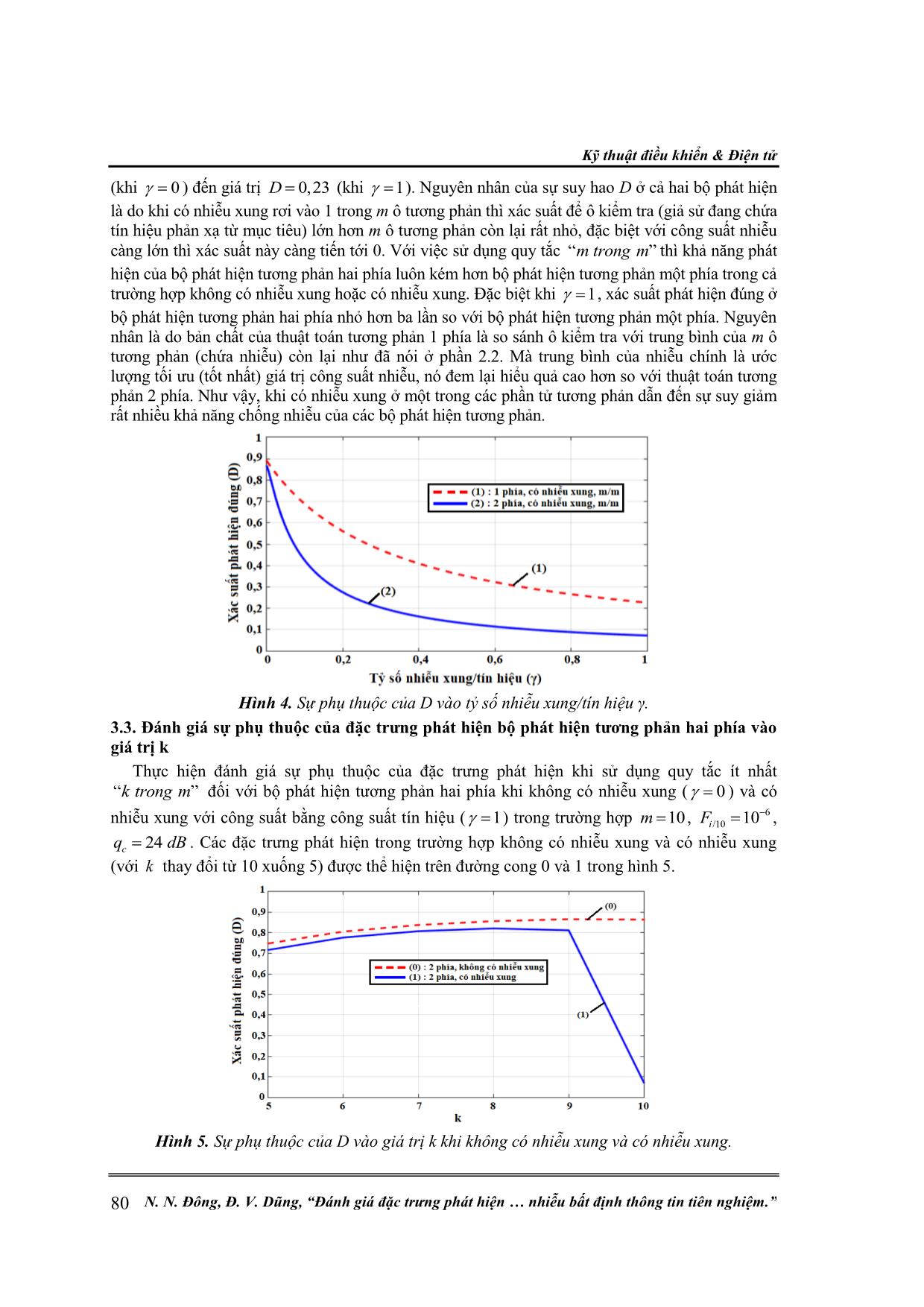
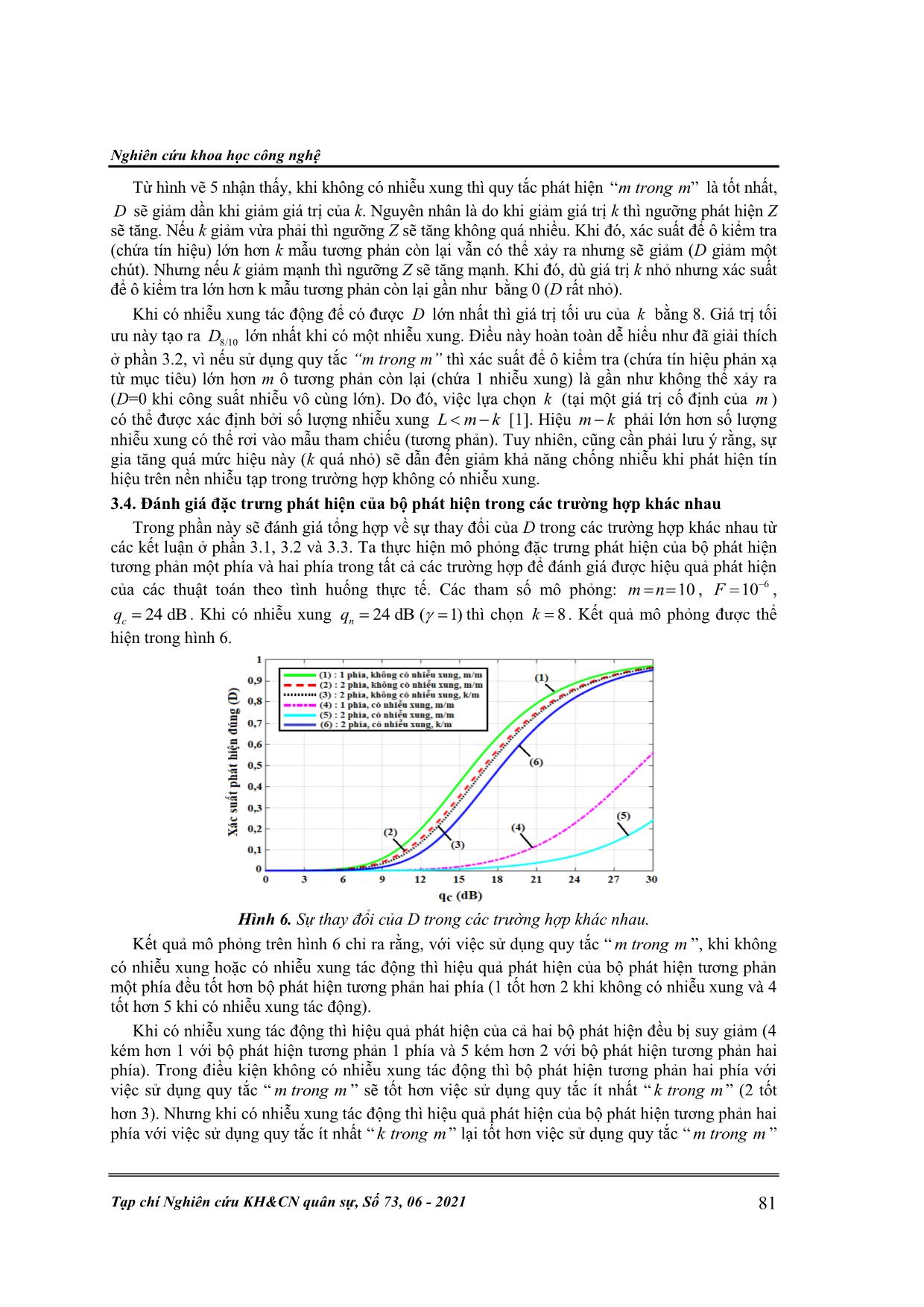
Kỹ thuật điều khiển & Điện tử 
 74 N. N. Đông, Đ. V. Dũng, “Đánh giá đặc trưng phát hiện  nhiễu bất định thông tin tiên nghiệm.” 
ĐÁNH GIÁ ĐẶC TRƯNG PHÁT HIỆN 
CỦA BỘ PHÁT HIỆN TƯƠNG PHẢN TÍN HIỆU 
TRÊN NỀN NHIỄU BẤT ĐỊNH THÔNG TIN TIÊN NGHIỆM 
Nguyễn Ngọc Đông1, Đinh Văn Dũng2* 
Tóm tắt: Bài toán nâng cao hiệu quả phát hiện tín hiệu có ích trên nền nhiễu bất định 
thông tin tiên nghiệm là một trong những vấn đề được quan tâm hàng đầu trong lĩnh vực 
xử lý tín hiệu ra đa và sonar. Một trong những phương pháp nâng cao hiệu quả phát hiện 
tín hiệu là sử dụng thuật toán tương phản. Bài báo trình bày thuật toán tương phản phát 
hiện tín hiệu xung đơn (trong miền thời gian) trên nền nhiễu tạp và nhiễu xung bất định 
thông tin tiên nghiệm. Hiệu quả của thuật toán tương phản phát hiện tín hiệu có ích trong 
các điều kiện khác nhau sẽ được đánh giá bằng mô phỏng trên phần mềm MATLAB thông 
qua sử dụng các biểu thức giải tích thể hiện đặc trưng phát hiện của chúng. 
Từ khóa: Phát hiện tín hiệu; Bất định thông tin tiên nghiệm; Thuật toán tương phản. 
1. ĐẶT VẤN ĐỀ 
Khả năng chống nhiễu của các bộ phát hiện tối ưu phần lớn phụ thuộc vào thông tin tiên 
nghiệm về các đặc trưng của tín hiệu và nhiễu (pha ban đầu, biên độ). Trong thực tế việc có được 
thông tin về các tham số của tín hiệu và nhiễu là ít xảy ra. Bên cạnh đó, nhiễu tạp có thể thường 
xuyên thay đổi theo thời gian và điều này gây khó khăn cho việc sử dụng các phương pháp tối ưu 
để phát hiện tín hiệu có ích [1]. Căn cứ vào sự có được các thông tin tiên nghiệm về tín hiệu và 
nhiễu, bài toán phát hiện được chia thành các dạng: phát hiện tham số; phát hiện phi tham số; 
phát hiện với bất định thông tin tiên nghiệm thiết yếu [2]. Trong trường hợp tổng quát, bất định 
thông tin tiên nghiệm được hiểu là sự thiếu thông tin tiên nghiệm về các tham số của hàm phân 
bố (trước hết là nhiễu). Các thuật toán tham số có thể vượt trội hơn đáng kể so với các thuật toán 
tham số về đặc trưng phát hiện do kết quả của việc bỏ qua thông tin tiên nghiệm. Mặt khác, các 
điều kiện làm việc trong thực tế luôn thay đổi nên có những loại nhiễu không giống với các loại 
nhiễu được sử dụng trong bộ tổng hợp các thuật toán tham số. Khi đó các thuật toán phi tham số 
thường tốt hơn nhiều so với các thuật toán tham số, thậm chí có trường hợp thuật toán tham số 
không làm việc. Các giải pháp đối với trường hợp bất định thông tin tiên nghiệm có thể được 
chia thành bốn nhóm: 
- Phương pháp thống kê tham số dựa trên các nguyên tắc tương tự, bất biến và minimax [3]; 
- Phương pháp thống kê phi tham số [4]; 
- Phương pháp thích nghi bằng cách sử dụng các mẫu thử [5]; 
- Phương pháp mạnh [6]. 
Các kết quả phân tích ưu điểm và nhược điểm của từng phương pháp đã được nhiều tác giả 
xem xét và đã chỉ ra rằng, vấn đề khó khăn nhất không chỉ đơn thuần là việc phải xác định được 
hàm phân bố của nhiễu, mặt khác phải đảm bảo tính ổn định và không tương quan giữa các mẫu 
nhiễu. Một trong những giải pháp để giải quyết vấn đề này đã được đề xuất trong bài toán phát 
hiện phi tham số, đó là thuật toán tương phản phát hiện tín hiệu xung trên nền nhiễu bất định 
thông tin tiên nghiệm [1] sẽ được trình bày dưới đây. 
2. NGHIÊN CỨU THUẬT TOÁN TƯƠNG PHẢN PHÁT HIỆN TÍN HIỆU RA ĐA XUNG 
ĐƠN TRÊN NỀN NHIỄU BẤT ĐỊNH THÔNG TIN TIÊN NGHIỆM 
 2.1. Thuật toán tương phản hai phía phát hiện tín hiệu với công suất nhiễu chưa biết 
Sơ đồ khối của bộ phát hiện sử dụng thuật toán tương phản hai phía với m phần tử tương 
phản trong miền thời gian [7] được thể hiện trong hình 1: 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 73, 06 - 2021 75 
Quyết định
SS . SS SS . SS
ηm ... η1+m/2 ηm/2 ... η1
ξm . ξ1
Có Không
ξ0 ξm/2 .ξ1+m/2
Z
Bộ lọc
phối hợp
Tách sóng
biên độ
y(t)
Hình 1. Sơ đồ khối bộ phát hiện tương phản hai phía với m phần tử. 
Hoạt động của nó khi phát hiện tín hiệu ra đa xung đơn như sau. Quá trình ngẫu nhiên với tín 
hiệu xung ở đầu vào qua bộ lọc phối hợp và tách sóng biên độ đi vào dây giữ chậm gồm 1m 
phần tử giữ chậm, với mỗi phần tử giữ chậm thời gian bằng độ rộng xung 
c . Do đó, 1m phần 
tử phân giải cự ly được tương ứng với các giá trị 
0 1, ,..., m   - Giá trị biên độ đường bao, sau đó 
các giá trị này được đưa đến thiết bị hình thành hàm tương phản 
1 2, ,..., m   , trong đó, 
1 0 1/   , 2 0 2/ ,...,   0 0 0/ ,m m     . Các hàm tương phản được đưa tới các bộ so 
sánh (SS) để so sánh với ngưỡng tương phản Z . Kết quả so sánh (ở dạng 1 - vượt ngưỡng và 0 - 
dưới ngưỡng) được đưa đến khối quyết định. Theo quy tắc quyết định phát hiện tín hiệu, ví dụ 
“ ”m trong m , một quyết định được đưa ra về sự có mặt của tín hiệu trong phần tử phân giải cự 
ly trung tâm. Việc sử dụng dây giữ chậm như một thiết bị tạo ra các giá trị mẫu của đường bao 
0 1, ,..., m   cho phép xử lý trượt (cửa sổ trượt) để có được các giá trị hiện tại của phát hiện thống 
kê (hàm tương phản , 1,i i m ) tuần tự theo thời g ... định về sự có mặt của tín hiệu có ích ở phần tử trung tâm trong dải cự ly cửa sổ 
trượt của bộ phát hiện được đưa ra khi mẫu 
0 lớn hơn (hoặc bằng giá trị ngưỡng Z ) ít nhất 
“ ”k trong m mẫu i và j thu được trong các phần tử phân giải (tương phản) liền kề ( k là số 
lượng mẫu tương phản nằm trong khoảng từ 1 đến 1m ). Khi sử dụng quy tắc quyết định này, 
mẫu tín hiệu có thể nhỏ hơn (giá trị ngưỡng Z ) một số mẫu tương phản (đặc biệt là những mẫu 
có chứa nhiễu xung mạnh). 
Xem xét hiệu quả của việc sử dụng quy tắc quyết định này với các điều kiện phát hiện như đã 
thảo luận ở trên (không có nhiễu xung). Theo định lý cộng và nhân xác suất [10] có tính đến tính 
bất định tiên nghiệm về thời điểm xuất hiện của nhiễu xung thì /k mD và /k mF 
đối với quy tắc 
quyết định này được xác định bằng các biểu thức sau [1]: 
/
1 1
! 1 ! 1
,
1 ! 1
k kk
m c c
k m m m
c c
l m k l m k
k C q m q
D
l q Z m k l q Z
  
 (7) 
/
1 1
! !
.
!
k
m
k m m m
l m k l m k
k C m
F
l Z m k l Z
  
 (8) 
Khi k m (mẫu tín hiệu lớn hơn tất cả các mẫu tương phản) thì các biểu thức (7) và (8) sẽ 
giống với các biểu thức (5) và (1). Khi đó, quy tắc ít nhất “ ”k trong m sẽ trở thành quy tắc 
“ ”m trong m . Tiếp theo chúng ta hãy xem xét hiệu quả của quy tắc quyết định ít nhất 
“ ”k trong m trong trường hợp có 1 nhiễu xung ở một trong các phần tử phân giải tương phản 
trong phạm vi cửa sổ trượt của bộ phát hiện tương phản. 
Thời gian xuất hiện của nhiễu xung là không xác định, nó có thể nằm ở một trong m phần tử 
tương phản với xác suất như nhau. Khi đó, 1/k mD sẽ được xác định như sau [1]: 
 
1 1
1 1
1 1 1
/ 1 1
1
1 1 1
.
1 1 1 1
m m
k k k
c c n
l m k l m k
k m m m
c c n c
l m k l m k
q l q q Z l
D
l q Z q q l q Z
 
 
 (9) 
Khi 0nq thì biểu thức (9) giống với (7), còn khi 0n cq q thì (9) giống với (8). 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 73, 06 - 2021 79 
 3. KẾT QUẢ MÔ PHỎNG 
Sử dụng phần mềm MATLAB để mô phỏng và so sánh đặc trưng phát hiện của các bộ phát 
hiện tương phản một phía và hai phía tín hiệu ra đa xung đơn. 
3.1. Đánh giá sự phụ thuộc của đặc trưng phát hiện vào số lượng phần tử tương phản 
Trên hình 3 thể hiện sự phụ thuộc của xác suất phát hiện đúng D tín hiệu trên nền nhiễu dừng 
có phân bố chuẩn (không có nhiễu xung) của bộ phát hiện tương phản hai phía sử dụng quy tắc 
“ ”m trong m vào số lượng các phần tử tương phản, với 610 .F 
Hình 3. Sự phụ thuộc của D vào số lượng phần tử tương phản m. 
Từ hình vẽ 3 thấy rằng, với cùng tỷ số tín/tạp xác xuất phát hiện đúng D tăng khi số lượng 
phần tử tương phản tăng. Để D=0,9 khi m=4 yêu cầu tỷ số tín/tạp 31 dBcq tăng 6 dB khi 
m=10 yêu cầu 25 dBcq . Tăng mạnh khi m tăng từ 2 đến 4, sau đó sẽ tăng ít dần. Nếu m đủ 
lớn thì đặc trưng phát hiện của bộ phát hiện tương phản hai phía sẽ tiệm cận đến đặc trưng phát 
hiện của bộ phát hiện tối ưu. Kết quả trên có được là do khi tăng giá trị m thì ngưỡng phát hiện Z 
giảm. Đối với ô kiểm tra chứa tín hiệu phản xạ từ mục tiêu thì với việc ngưỡng giảm, xác suất để 
mẫu kiểm tra lớn hơn m mẫu tương phản còn lại rất cao (hoàn toàn có thể xảy ra), khi đó, D sẽ 
tăng. Còn với các mẫu tương phản, tuy ngưỡng giảm nhưng chúng chỉ chứa nhiễu tạp nên xác 
suất để mỗi mẫu tương phản này hơn m mẫu còn lại là rất nhỏ. Như vậy, việc lựa chọn m có thể 
đạt được đặc trưng phát hiện mong muốn nhưng cũng phải đảm bảo tốc độ tính toán và mức độ 
phức tạp trong sơ đồ bộ phát hiện. Trong thực tế thường lựa chọn giá trị tối ưu 10m . 
3.2. Đánh giá sự phụ thuộc của đặc trưng phát hiện vào công suất nhiễu xung 
Thực hiện đánh giá hiệu quả của các bộ phát hiện tương phản một phía và hai phía khi có 
nhiễu xung tác động sử dụng quy tắc “ ”m trong m . Trên hình vẽ 4 thể hiện sự phụ thuộc của xác 
suất phát hiện đúng D vào tỷ số  (tỷ số nhiễu xung/tín hiệu) trong trường hợp 24 cq dB và 
610 .F Kết quả đường cong 1 và 2 trong hình 4 tương ứng đặc trưng phát hiện của bộ phát 
hiện tương phản một phía và hai phía phụ thuộc vào tỷ số công suất nhiễu xung/tín hiệu. 
Từ hình 4 thấy rằng, xác suất phát hiện đúng ở bộ phát hiện tương phản hai phía giảm từ giá trị 
0,86D (khi không có nhiễu xung 0 ) xuống 0,08D (khi công suất nhiễu xung bằng công 
suất tín hiệu 1 ). Trong khi đó, ở bộ phát hiện tương phản một phía giảm từ giá trị 0,89D 
Kỹ thuật điều khiển & Điện tử 
 80 N. N. Đông, Đ. V. Dũng, “Đánh giá đặc trưng phát hiện  nhiễu bất định thông tin tiên nghiệm.” 
(khi 0 ) đến giá trị 0,23D (khi 1 ). Nguyên nhân của sự suy hao D ở cả hai bộ phát hiện 
là do khi có nhiễu xung rơi vào 1 trong m ô tương phản thì xác suất để ô kiểm tra (giả sử đang chứa 
tín hiệu phản xạ từ mục tiêu) lớn hơn m ô tương phản còn lại rất nhỏ, đặc biệt với công suất nhiễu 
càng lớn thì xác suất này càng tiến tới 0. Với việc sử dụng quy tắc “ ”m trong m thì khả năng phát 
hiện của bộ phát hiện tương phản hai phía luôn kém hơn bộ phát hiện tương phản một phía trong cả 
trường hợp không có nhiễu xung hoặc có nhiễu xung. Đặc biệt khi 1 , xác suất phát hiện đúng ở 
bộ phát hiện tương phản hai phía nhỏ hơn ba lần so với bộ phát hiện tương phản một phía. Nguyên 
nhân là do bản chất của thuật toán tương phản 1 phía là so sánh ô kiểm tra với trung bình của m ô 
tương phản (chứa nhiễu) còn lại như đã nói ở phần 2.2. Mà trung bình của nhiễu chính là ước 
lượng tối ưu (tốt nhất) giá trị công suất nhiễu, nó đem lại hiểu quả cao hơn so với thuật toán tương 
phản 2 phía. Như vậy, khi có nhiễu xung ở một trong các phần tử tương phản dẫn đến sự suy giảm 
rất nhiều khả năng chống nhiễu của các bộ phát hiện tương phản. 
Hình 4. Sự phụ thuộc của D vào tỷ số nhiễu xung/tín hiệu γ. 
3.3. Đánh giá sự phụ thuộc của đặc trưng phát hiện bộ phát hiện tương phản hai phía vào 
giá trị k 
Thực hiện đánh giá sự phụ thuộc của đặc trưng phát hiện khi sử dụng quy tắc ít nhất 
“ ”k trong m đối với bộ phát hiện tương phản hai phía khi không có nhiễu xung ( 0 ) và có 
nhiễu xung với công suất bằng công suất tín hiệu ( 1 ) trong trường hợp 10m , 6/10 10iF
 , 
24cq dB . Các đặc trưng phát hiện trong trường hợp không có nhiễu xung và có nhiễu xung 
(với k thay đổi từ 10 xuống 5) được thể hiện trên đường cong 0 và 1 trong hình 5. 
Hình 5. Sự phụ thuộc của D vào giá trị k khi không có nhiễu xung và có nhiễu xung. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 73, 06 - 2021 81 
Từ hình vẽ 5 nhận thấy, khi không có nhiễu xung thì quy tắc phát hiện “ ”m trong m là tốt nhất, 
D sẽ giảm dần khi giảm giá trị của k. Nguyên nhân là do khi giảm giá trị k thì ngưỡng phát hiện Z 
sẽ tăng. Nếu k giảm vừa phải thì ngưỡng Z sẽ tăng không quá nhiều. Khi đó, xác suất để ô kiểm tra 
(chứa tín hiệu) lớn hơn k mẫu tương phản còn lại vẫn có thể xảy ra nhưng sẽ giảm (D giảm một 
chút). Nhưng nếu k giảm mạnh thì ngưỡng Z sẽ tăng mạnh. Khi đó, dù giá trị k nhỏ nhưng xác suất 
để ô kiểm tra lớn hơn k mẫu tương phản còn lại gần như bằng 0 (D rất nhỏ). 
Khi có nhiễu xung tác động để có được D lớn nhất thì giá trị tối ưu của k bằng 8. Giá trị tối 
ưu này tạo ra 
8/10D 
lớn nhất khi có một nhiễu xung. Điều này hoàn toàn dễ hiểu như đã giải thích 
ở phần 3.2, vì nếu sử dụng quy tắc “m trong m” thì xác suất để ô kiểm tra (chứa tín hiệu phản xạ 
từ mục tiêu) lớn hơn m ô tương phản còn lại (chứa 1 nhiễu xung) là gần như không thể xảy ra 
(D=0 khi công suất nhiễu vô cùng lớn). Do đó, việc lựa chọn k (tại một giá trị cố định của m ) 
có thể được xác định bởi số lượng nhiễu xung L m k [1]. Hiệu m k phải lớn hơn số lượng 
nhiễu xung có thể rơi vào mẫu tham chiếu (tương phản). Tuy nhiên, cũng cần phải lưu ý rằng, sự 
gia tăng quá mức hiệu này (k quá nhỏ) sẽ dẫn đến giảm khả năng chống nhiễu khi phát hiện tín 
hiệu trên nền nhiễu tạp trong trường hợp không có nhiễu xung. 
3.4. Đánh giá đặc trưng phát hiện của bộ phát hiện trong các trường hợp khác nhau 
Trong phần này sẽ đánh giá tổng hợp về sự thay đổi của D trong các trường hợp khác nhau từ 
các kết luận ở phần 3.1, 3.2 và 3.3. Ta thực hiện mô phỏng đặc trưng phát hiện của bộ phát hiện 
tương phản một phía và hai phía trong tất cả các trường hợp để đánh giá được hiệu quả phát hiện 
của các thuật toán theo tình huống thực tế. Các tham số mô phỏng: 10m n , 610F , 
24 dBcq . Khi có nhiễu xung 24 dBnq ( 1) thì chọn 8k . Kết quả mô phỏng được thể 
hiện trong hình 6. 
Hình 6. Sự thay đổi của D trong các trường hợp khác nhau. 
Kết quả mô phỏng trên hình 6 chỉ ra rằng, với việc sử dụng quy tắc “ m trong m ”, khi không 
có nhiễu xung hoặc có nhiễu xung tác động thì hiệu quả phát hiện của bộ phát hiện tương phản 
một phía đều tốt hơn bộ phát hiện tương phản hai phía (1 tốt hơn 2 khi không có nhiễu xung và 4 
tốt hơn 5 khi có nhiễu xung tác động). 
Khi có nhiễu xung tác động thì hiệu quả phát hiện của cả hai bộ phát hiện đều bị suy giảm (4 
kém hơn 1 với bộ phát hiện tương phản 1 phía và 5 kém hơn 2 với bộ phát hiện tương phản hai 
phía). Trong điều kiện không có nhiễu xung tác động thì bộ phát hiện tương phản hai phía với 
việc sử dụng quy tắc “ m trong m ” sẽ tốt hơn việc sử dụng quy tắc ít nhất “ k trong m ” (2 tốt 
hơn 3). Nhưng khi có nhiễu xung tác động thì hiệu quả phát hiện của bộ phát hiện tương phản hai 
phía với việc sử dụng quy tắc ít nhất “ k trong m ” lại tốt hơn việc sử dụng quy tắc “ m trong m ” 
Kỹ thuật điều khiển & Điện tử 
 82 N. N. Đông, Đ. V. Dũng, “Đánh giá đặc trưng phát hiện  nhiễu bất định thông tin tiên nghiệm.” 
(6 tốt hơn 5). Hơn thế nữa, nó còn tốt hơn cả hiệu quả phát hiện của bộ phát hiện tương phản một 
phía (6 tốt hơn 4). Đây chính là ưu điểm của quy tắc phát hiện ít nhất “ k trong m ” đã được trình 
bày trong phần tối ưu hóa thuật toán phát hiện tương phản hai phía trong điều kiện có nhiễu xung 
tác động. 
4. KẾT LUẬN 
Nội dung bài báo đã đưa ra phương pháp tiếp cận và nhận được các biểu thức giải tích đánh 
giá khả năng chống nhiễu của bộ phát hiện tương phản trên nền nhiễu với các đặc trưng chưa biết 
trước trong các trường hợp khác nhau. 
Trong điều kiện có nhiễu dừng phân bố chuẩn với giá trị trung bình bằng 0 và công suất chưa 
biết trước, F không phụ thuộc vào công suất của nhiễu nhưng được xác định thông qua ngưỡng 
tương phản Z và số phần tử tương phản m trong cửa sổ trượt của bộ phát hiện tương phản. D 
trong trường hợp này phụ thuộc vào F (thông qua các tham số Z và m ) và tỷ số tín hiệu/tạp 
cq . Hơn nữa, nếu cố định F thì khả năng chống nhiễu của bộ phát hiện với số phần tử tương 
phản 10m có xu hướng đạt đến khả năng chống nhiễu của bộ phát hiện tối ưu (trong điều kiện 
đã biết trước công suất nhiễu). 
Sự có mặt của nhiễu xung với công suất và thời gian đến chưa biết trước trong các phần tử 
tương phản của bộ phát hiện tương phản hai phía và khi sử dụng quy tắc “ m trong m ” dẫn đến 
suy giảm khả năng chống nhiễu, nó phụ thuộc vào công suất nhiễu xung. Để giảm thiểu những 
tổn thất này, quy tắc ít nhất “ k trong m ” được sử dụng. Giá trị k được chọn từ điều kiện 
k m L , trong đó, L là số nhiễu xung có thể rơi vào các phần tử tương phản của bộ phát hiện. 
Những ưu điểm nhất định của phương pháp tương phản là do việc sử dụng thống kê phát hiện 
có tính bất biến cực đại bằng cách so sánh thống kê phát hiện riêng lẻ (hàm tương phản) với một 
giá trị ngưỡng. Nó đem lại những lợi thế nêu trên và tạo được tính linh hoạt trong việc ra quyết 
định và ngoài ra có thể sử dụng các ngưỡng khác nhau cho các thống kê khác nhau, điều chỉnh 
theo tình huống nhiễu. Các tính chất tích cực của phương pháp tương phản hai phía được nêu ra 
ở trên cho phép chúng ta kết luận rằng phương pháp này có khả năng làm việc hiệu quả trong các 
điều kiện bất định thông tin tiên nghiệm. 
TÀI LIỆU THAM KHẢO 
[1]. Белецкий Ю.С., “Методы и алгоритмы контрастного обнаружения сигналов на 
фоне помех с априори неизвестными характерисками”, М.: Радиотехника, 2011. 
[2]. Под ред. А.А. Елисеева, А.А. Оводенко,“Управление движущимеся объектами”, М.: 
Изд. Мир книги, 1994. 
[3]. Ширман ЯД., ГоликовВ.Н., “Основы теории обнаружения радиолокационных 
сигналов и измерения их параметров”, М.: Сов. Радио, 1977. 
[4]. Акимов П.С., Бакут П.А., “Теория обнаружения сигналов”, М.: Радио и связь, 1984. 
[5]. Левин Б.Р., “Теоретические основы статистической радиотехники” Кн.З. М.: Сов. 
Радио, 1976. 
[6]. Оводенкко А.А., “Робастные локационные устройства”, Л.: Изд. ЛГУ, 1981. 
[7]. Белецкий Ю.С., Белоусов А.А., “Контрастное обнаружение флуктуирующего 
сигнала в шумах с произвольным энергетическим спектром”, Доклад 1X 
Всесоюзной акустической конференции, М.: Секция-С, 1977, С. 37-40. 
[8]. Венцель Е С., Гончаров Л.А., “Теория вероятностей”, М.: Наука, 1973. 
[9]. Сидоров Ю.Е., “Оптимальный алгоритм обнаружения радиолокационных сигналов в 
шумах неизвестной интенсивности”, Известия вузов. Сер. Ра-диоэлектроника, 1973, 
№ 2, С. 101-104. 
[10]. Вентцель Е.С., “Теория вероятностей”, М.: Физматгиз, 1962. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 73, 06 - 2021 83 
[11]. Luo, Z., Lu, P. & Zhang, G., “Locally optimal detector design in impulsive noise with 
unknown distribution”, EURASIP J. Adv. Signal Process. 34 (2018). 
https://doi.org/10.1186/s13634-018-0560-x, 2018. 
[12]. Liberios Vokorokos; Alexander Ivchenko; Stanislav Marchevský; Elena Palahina; 
Volodymyr Palahin, “Parameters estimation of correlated non-Gaussian processes by the 
method of polynomial maximisation”, IET Signal Processing, Volume 11, Issue 3, May 
2017, p. 313 – 319. 
[13]. Gencheng Guo, Mrinal Mandal, Yindi Jing, “A robust detector of known signal in non-
Gaussian noise using threshold systems”, Signal Processing 92 (2012) 2676–2688. 
ABSTRACT 
EVALUATION OF DETECTION PERFORMANCE OF CONTRAST DETECTOR 
FOR SIGNALS AGAINST THE INTERFERENCE BACKGROUND 
WITH PRIORI UNKNOWN CHARACTERISTICS 
The problem of improving the efficiency of detecting useful signals against the 
interference background with a priori unknown characteristics is one of the top concerns 
of radar and sonar signal processing. One of the methods to improve signal detection 
efficiency is to use contrast algorithm. In this paper, the contrast algorithm for detection 
of single pulse signal (in time domain) on the noise and pulse interference background 
with a priori unknown characteristics is presented. The effectiveness of the contrast 
algorithm for detection of useful signal under different conditions will be evaluated by 
simulation on MATLAB software using the analytical expressions that represent their 
detection characteristics. 
Keywords: Detection of signal; A priori characteristics uncertainty; Contrast algorithm. 
Nhận bài ngày 11 tháng 01 năm 2021 
Hoàn thiện ngày 02 tháng 6 năm 2021 
Chấp nhận đăng ngày 10 tháng 6 năm 2021 
Địa chỉ: 1Khoa Vô tuyến điện tử - Học viện Kỹ thuật quân sự; 
2
Khoa Vô tuyến điện tử - Trường Sĩ quan Không quân. 
*
Email: dinhvandung.tb@gmail.com.