Bài giảng Mạch điện tử - Chương 3: Các phương pháp phân tích mạch điện
Phương pháp dòng điện nhánh:
• Ẩn số là dòng điện nhánh
• Phương pháp:
- Xác định số nhánh (tùy ý chọn chiều dòng điện trong các nhánh)
- Xác định số nút và số vòng độc lập (vòng độc lập thường chọn là các mắt lưới)
Giả sử mạch có m nhánh và n nút, cần có m phương trình để giải m ẩn
- Viết (n – 1) phương trình Kirhof 1 cho (n – 1) nút
- Viết (m – n + 1) phương trình Kirhof 2 cho (m – n + 1) mắt lưới
- Giải hệ m phương trình tìm các dòng điện nhánh.
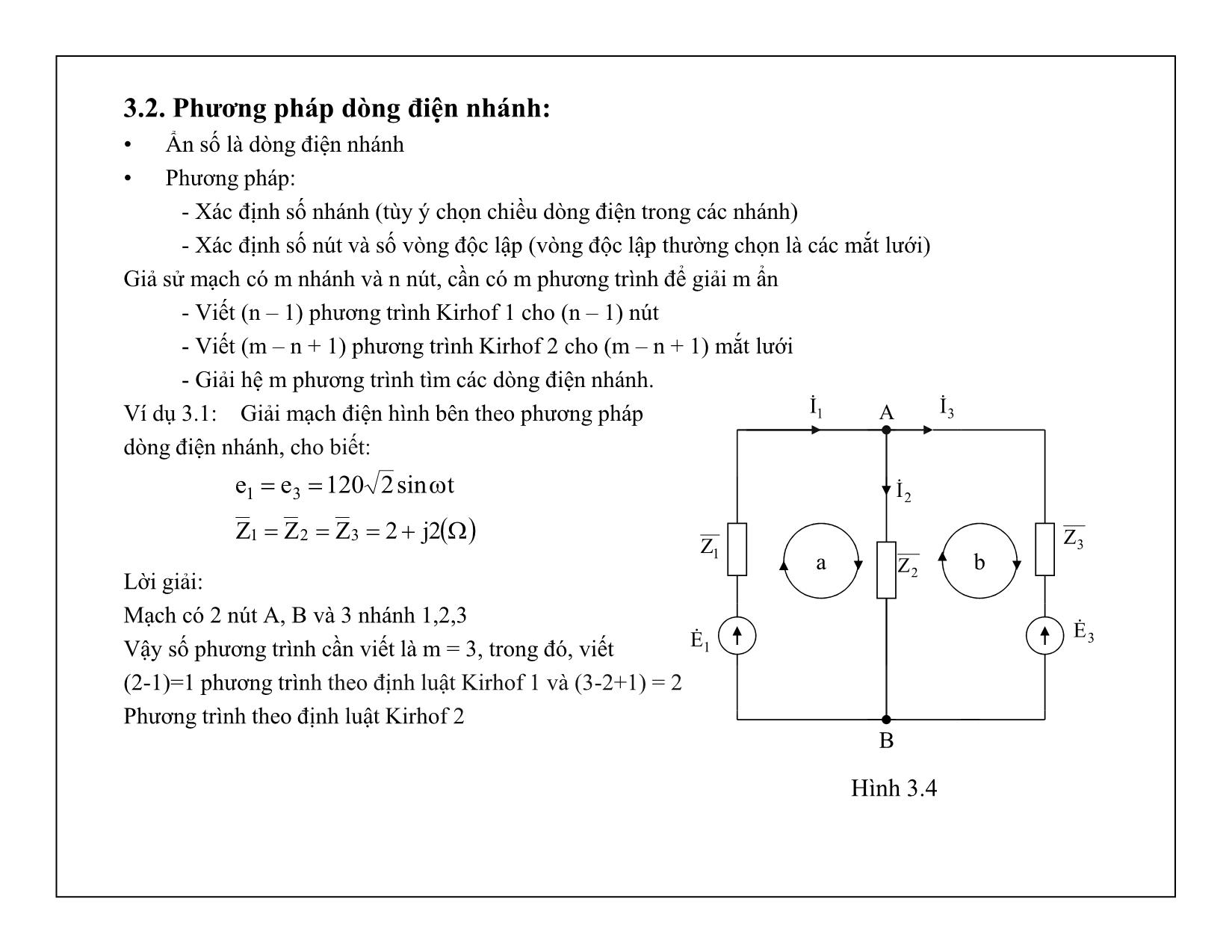
Ví dụ 3.1: Giải mạch điện hình bên theo phương pháp
dòng điện nhánh, cho biết:
Lời giải:
Mạch có 2 nút A, B và 3 nhánh 1,2,3
Vậy số phương trình cần viết là m = 3, trong đó, viết
(2-1)=1 phương trình theo định luật Kirhof 1 và (3-2+1) = 2
Phương trình theo định luật Kirhof 2
Trang 1
Trang 2

Trang 3
Trang 4

Trang 5
Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tóm tắt nội dung tài liệu: Bài giảng Mạch điện tử - Chương 3: Các phương pháp phân tích mạch điện
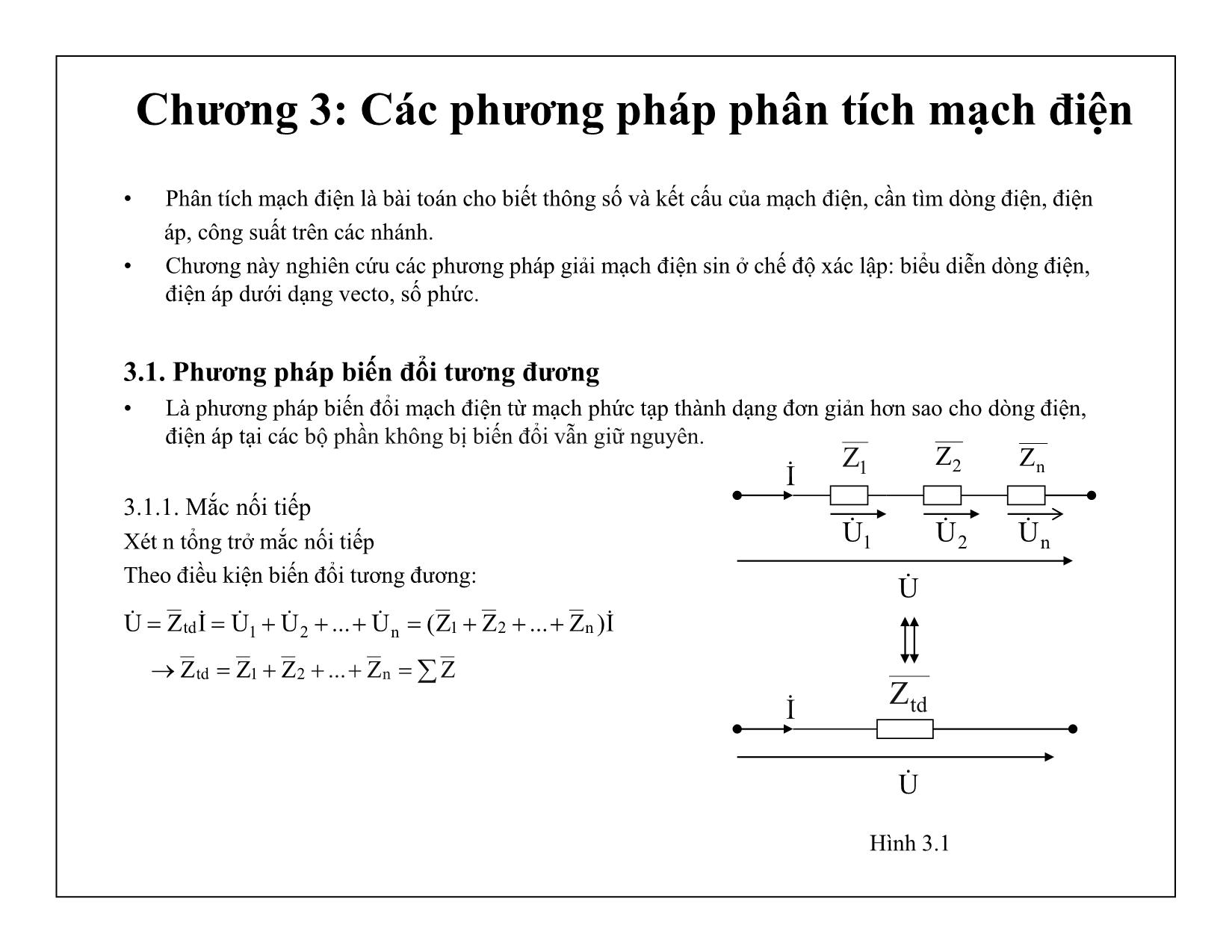
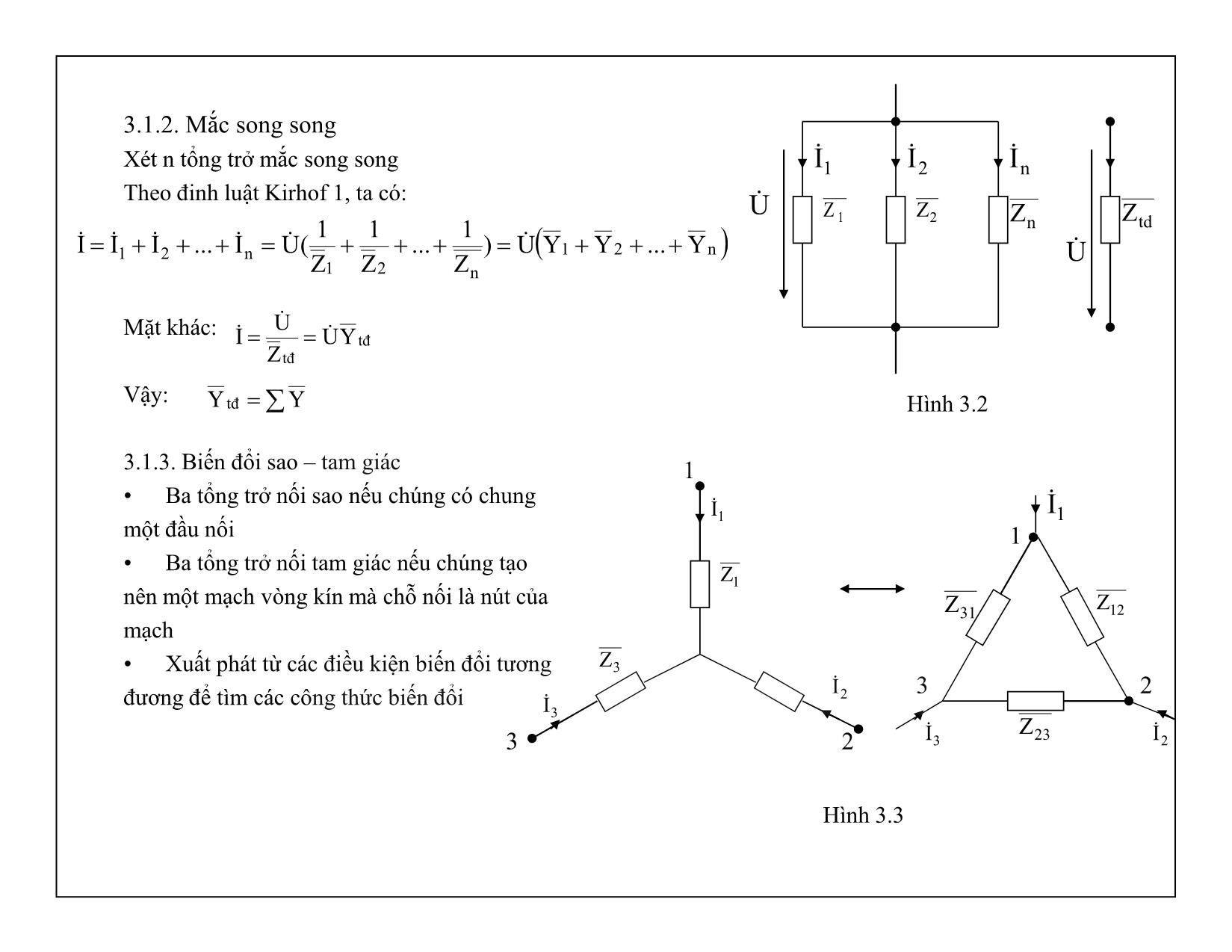
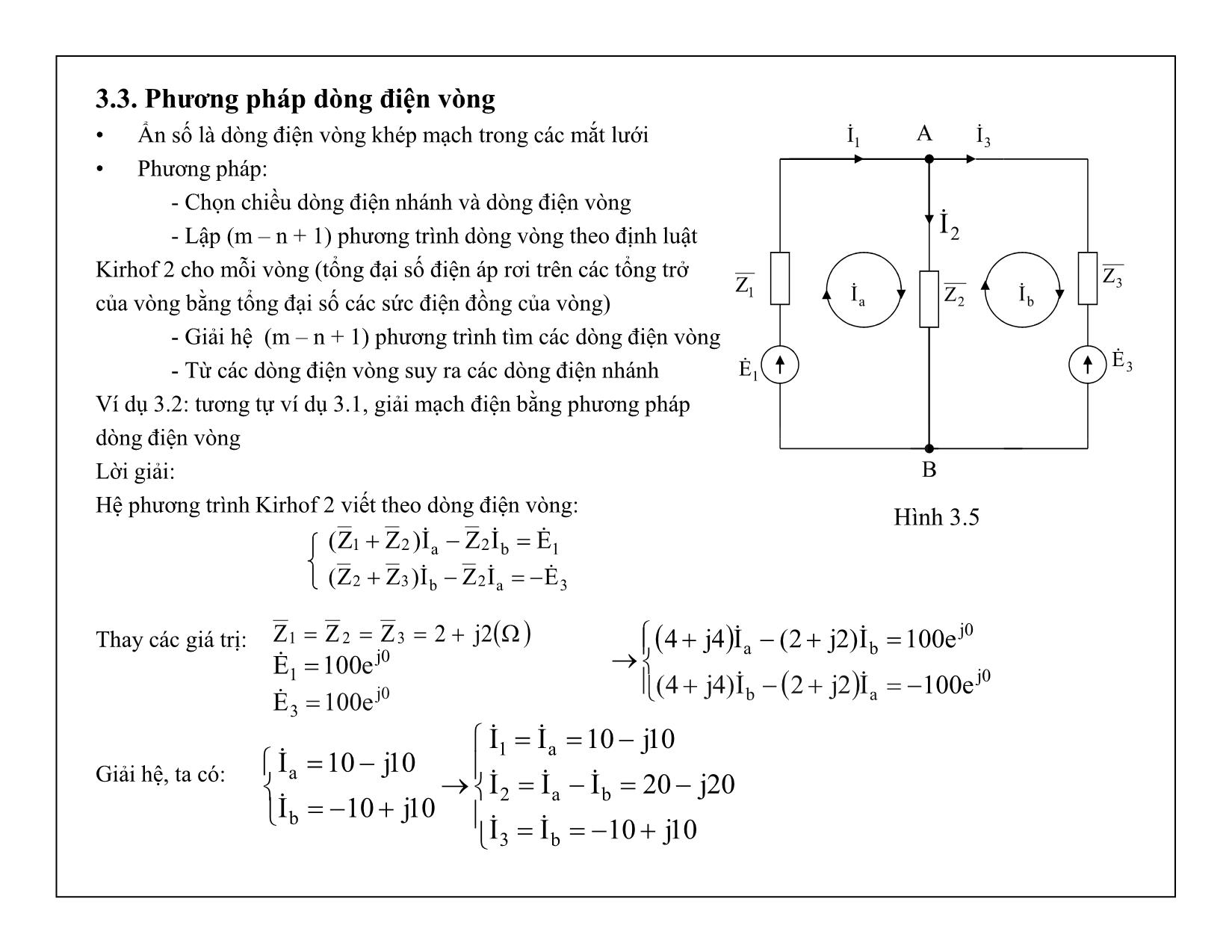
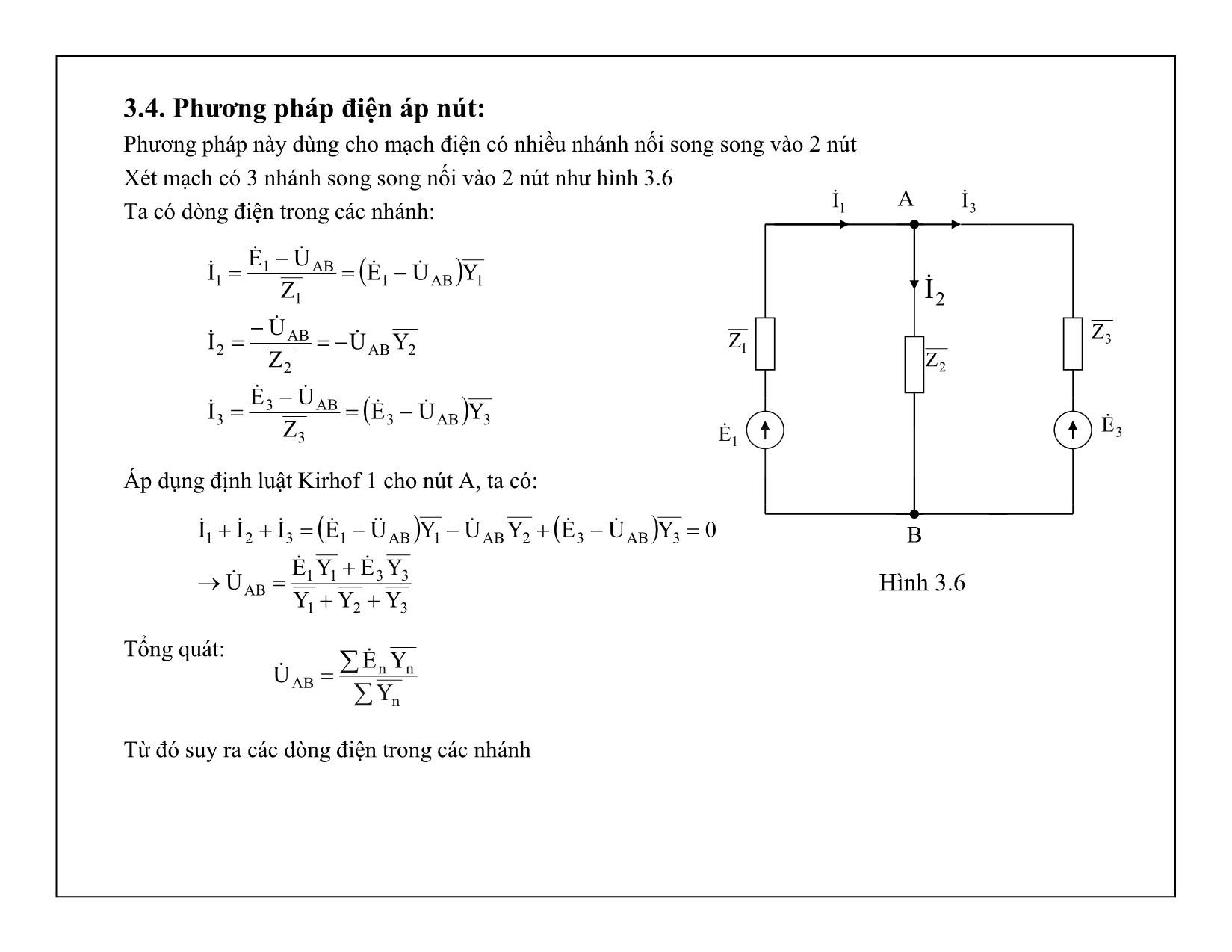
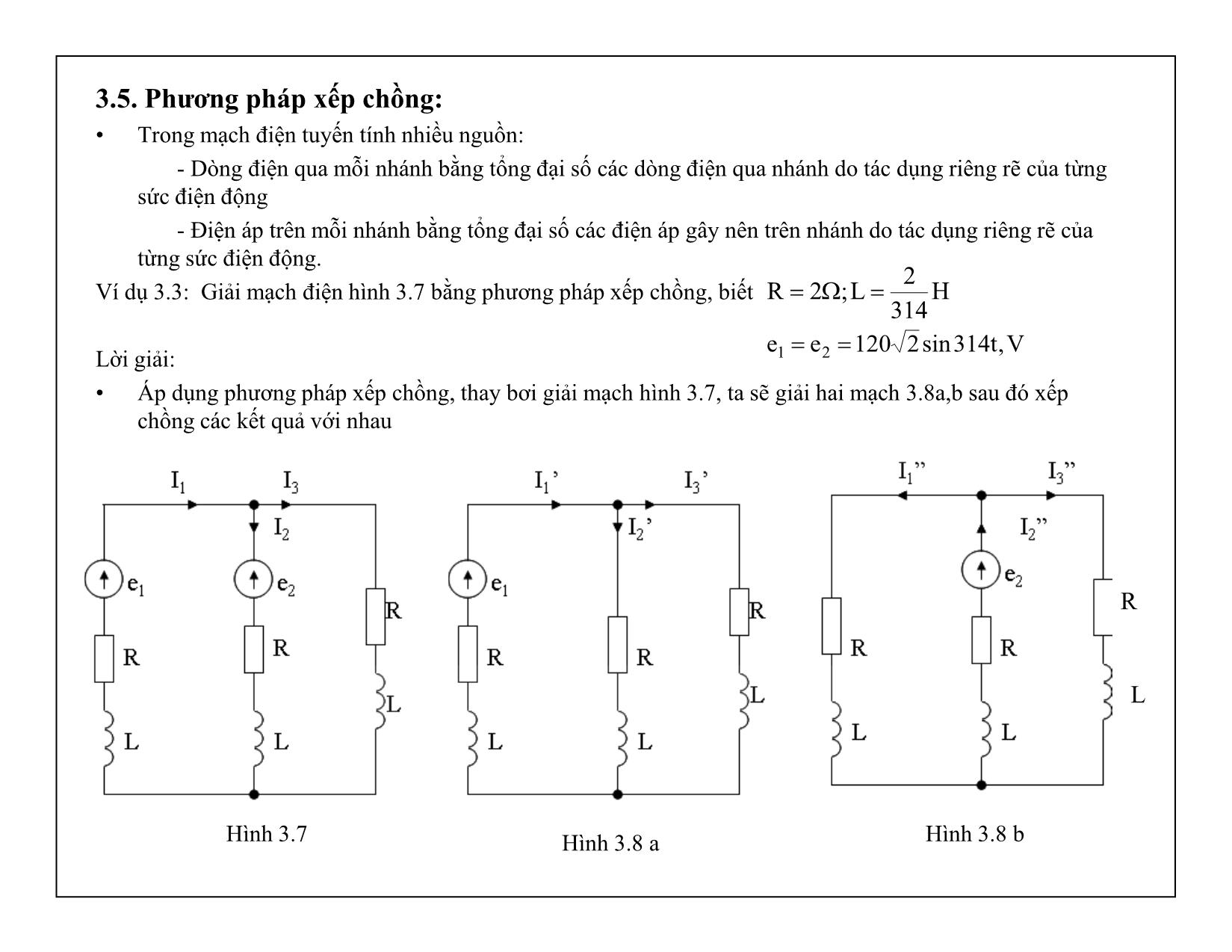
Chương 3: Các phương pháp phân tích mạch điện • Phân tích mạch điện là bài toán cho biết thông số và kết cấu của mạch điện, cần tìm dòng điện, điện áp, công suất trên các nhánh. • Chương này nghiên cứu các phương pháp giải mạch điện sin ở chế độ xác lập: biểu diễn dòng điện, điện áp dưới dạng vecto, số phức. 3.1. Phương pháp biến đổi tương đương • Là phương pháp biến đổi mạch điện từ mạch phức tạp thành dạng đơn giản hơn sao cho dòng điện, điện áp tại các bộ phần không bị biến đổi vẫn giữ nguyên. 3.1.1. Mắc nối tiếp Xét n tổng trở mắc nối tiếp Theo điều kiện biến đổi tương đương: tdZ U I I)Z...ZZ(U...UUIZU n21n21td ZZ...ZZZ n21td 2Z nZ1Z nU1U 2U U I Hình 3.1 3.1.2. Mắc song song Xét n tổng trở mắc song song Theo đinh luật Kirhof 1, ta có: Mặt khác: Vậy: 3.1.3. Biến đổi sao – tam giác • Ba tổng trở nối sao nếu chúng có chung một đầu nối • Ba tổng trở nối tam giác nếu chúng tạo nên một mạch vòng kín mà chỗ nối là nút của mạch • Xuất phát từ các điều kiện biến đổi tương đương để tìm các công thức biến đổi n21 n21 n21 Y...YYU)Z 1...Z 1 Z 1(UI...III tđ tđ YUZ UI YY tđ U 1Z 2Z nZ tdZ U 1I 2I nI 1I 1Z 2I 3Z 3I 1 23 Hình 3.2 Hình 3.3 31Z 12Z 23Z 1I 2I3I 3 1 2 • Cho Theo hình sao: Theo hình tam giác: Suy ra: • Tương tự, lần lượt cho , và viết các phương trình cân bằng điện áp. Các công thức biến đổi tương đương giữa hình tam giác và hình sao: 0I1 32223 ZZIU 233112223 Z//ZZIU 312312 23311232 ZZZ ZZZZZ 312312 31121 ZZZ Z.ZZ 312312 23122 ZZZ Z.ZZ 312312 31233 ZZZ Z.ZZ 0I2 0I3 Tổng trở của nhánh hình sao tương đương bằng tích hai tổng trở tam giác kẹp nó chia cho tổng ba tổng trở tam giác 3 212112 Z Z.ZZZZ 1 323223 Z Z.ZZZZ 2 131331 Z Z.ZZZZ Tổng trở của nhánh tam giác tương đương bằng hai tổng trở hình sao nối với nó cộng với tích cảu chúng chia cho tổng trở của nhánh kia 3.2. Phương pháp dòng điện nhánh: • Ẩn số là dòng điện nhánh • Phương pháp: - Xác định số nhánh (tùy ý chọn chiều dòng điện trong các nhánh) - Xác định số nút và số vòng độc lập (vòng độc lập thường chọn là các mắt lưới) Giả sử mạch có m nhánh và n nút, cần có m phương trình để giải m ẩn - Viết (n – 1) phương trình Kirhof 1 cho (n – 1) nút - Viết (m – n + 1) phương trình Kirhof 2 cho (m – n + 1) mắt lưới - Giải hệ m phương trình tìm các dòng điện nhánh. Ví dụ 3.1: Giải mạch điện hình bên theo phương pháp dòng điện nhánh, cho biết: Lời giải: Mạch có 2 nút A, B và 3 nhánh 1,2,3 Vậy số phương trình cần viết là m = 3, trong đó, viết (2-1)=1 phương trình theo định luật Kirhof 1 và (3-2+1) = 2 Phương trình theo định luật Kirhof 2 B 1E A a b1Z 2Z 3Z 1I 2I 3I 3E Hình 3.4 tsin2120ee 31 2j2ZZZ 321 Ta có hệ 3 phương trình: Thay các giá trị: Ta có: Giải hệ phương trình trên, ta có: 0j 1 e100E 0III 321 12211 EIZIZ 33312 EIZIZ 0j 3 e100E A2101010I 10j10I 22 1 1 A2101010I 10j10I 22 3 3 A2202020I 20j20I 22 2 2 2j2ZZZ 321 0III 321 0j21 e100II)2j2( 0j31 e100II2j2 3.3. Phương pháp dòng điện vòng • Ẩn số là dòng điện vòng khép mạch trong các mắt lưới • Phương pháp: - Chọn chiều dòng điện nhánh và dòng điện vòng - Lập (m – n + 1) phương trình dòng vòng theo định luật Kirhof 2 cho mỗi vòng (tổng đại số điện áp rơi trên các tổng trở của vòng bằng tổng đại số các sức điện đồng của vòng) - Giải hệ (m – n + 1) phương trình tìm các dòng điện vòng - Từ các dòng điện vòng suy ra các dòng điện nhánh Ví dụ 3.2: tương tự ví dụ 3.1, giải mạch điện bằng phương pháp dòng điện vòng Lời giải: Hệ phương trình Kirhof 2 viết theo dòng điện vòng: Thay các giá trị: Giải hệ, ta có: Hình 3.5 1b2a21 EIZI)ZZ( 3a2b32 EIZI)ZZ( 2j2ZZZ 321 0j 1 e100E 0j 3 e100E 0j ab 0j ba e100I2j2I)4j4( e100I)2j2(I4j4 10j10II 20j20III 10j10II 10j10I 10j10I b3 ba2 a1 b a aI 1E A B 1Z 2Z 3 Z 1I 2I 3I 3E bIa 3.4. Phương pháp điện áp nút: Phương pháp này dùng cho mạch điện có nhiều nhánh nối song song vào 2 nút Xét mạch có 3 nhánh song song nối vào 2 nút như hình 3.6 Ta có dòng điện trong các nhánh: Áp dụng định luật Kirhof 1 cho nút A, ta có: Tổng quát: Từ đó suy ra các dòng điện trong các nhánh 3AB3 3 AB33 2AB 2 AB2 1AB1 1 AB11 YUEZ UEI YUZ UI YUEZ UEI 1E A B 1Z 2Z 3Z 1I 2I 3I 3E Hình 3.6 321 3311AB 3AB32AB1AB1321 YYY YEYEU 0YUEYUYUEIII n nnAB Y YEU 3.5. Phương pháp xếp chồng: • Trong mạch điện tuyến tính nhiều nguồn: - Dòng điện qua mỗi nhánh bằng tổng đại số các dòng điện qua nhánh do tác dụng riêng rẽ của từng sức điện động - Điện áp trên mỗi nhánh bằng tổng đại số các điện áp gây nên trên nhánh do tác dụng riêng rẽ của từng sức điện động. Ví dụ 3.3: Giải mạch điện hình 3.7 bằng phương pháp xếp chồng, biết Lời giải: • Áp dụng phương pháp xếp chồng, thay bơi giải mạch hình 3.7, ta sẽ giải hai mạch 3.8a,b sau đó xếp chồng các kết quả với nhau H314 2L;2R V,t314sin2120ee 21 Hình 3.8 a Hình 3.8 bHình 3.7 R L • Mạch 3.8 a: chỉ có sức điện động e1 tác động: Từ các thông số đã cho, ta có: • Mạch 3.8 b, chỉ có sức điện động e2 tác động, tương tự như trên, ta tính được: • Xếp chồng các kết quả, ta có: A10j10II A20j20I " 3 " 1 " 2 2j2jXRZZZ 2314 2.314LX L321 L A10j102 III A20j201j12j2 120 ZZ EI ' 1'3 ' 2 tđ231 1'1 A2101010I 10j1010j1020j20III 22 1 " 1 ' 11 A2202020I 20j2010j1010j10III 22 3 " 3 ' 33 A2101010I 10j1020j2010j10III 22 1 " 2 ' 22 3.6. Phương pháp tính mạch có nguồn chu kỳ không sin: • Trong kỹ thuật điện, điện tử thương gặp các nguồn chu kỳ không sin. Để phân tích các mạch này, ta áp dụng nguyên lý xếp chồng. • Phương pháp: - Phân tích nguồn không sin thành tổng các điều hòa có tần số khác nhau: - Cho từng điều hòa tác động, tìm dòng điện, điện áp do từng điều hòa tạo nên. - Tổng hợp kết quả kkm2m21m1o tksinE...t2sinEtsinEEte Thành phần một chiều Thành phần cơ bản có tần số bằng tần số nguồn không sin Các thành phần bậc cao
File đính kèm:
 bai_giang_mach_dien_tu_chuong_3_cac_phuong_phap_phan_tich_ma.pdf
bai_giang_mach_dien_tu_chuong_3_cac_phuong_phap_phan_tich_ma.pdf

