Bài giảng Trường điện từ - Chương 3: Trường điện từ dừng - Nguyễn Thị Linh Phương
Chia thành 2 nhóm : Trường từ dừng & trường điện dừng
o Trường từ dừng gây bởi dòng điện dẫn không đổi
theo thời gian. 77 7 /. 7; /v 7; 77
6 rot H = J\divB = 0'8 = ụH
o Trường điện dừng trong môi trường dần có dòng điện không đôi. rot g _ 0. divj = 0. J = y£
o Trường điện dừng trong điện môi lý tưởng.

Trang 1

Trang 2
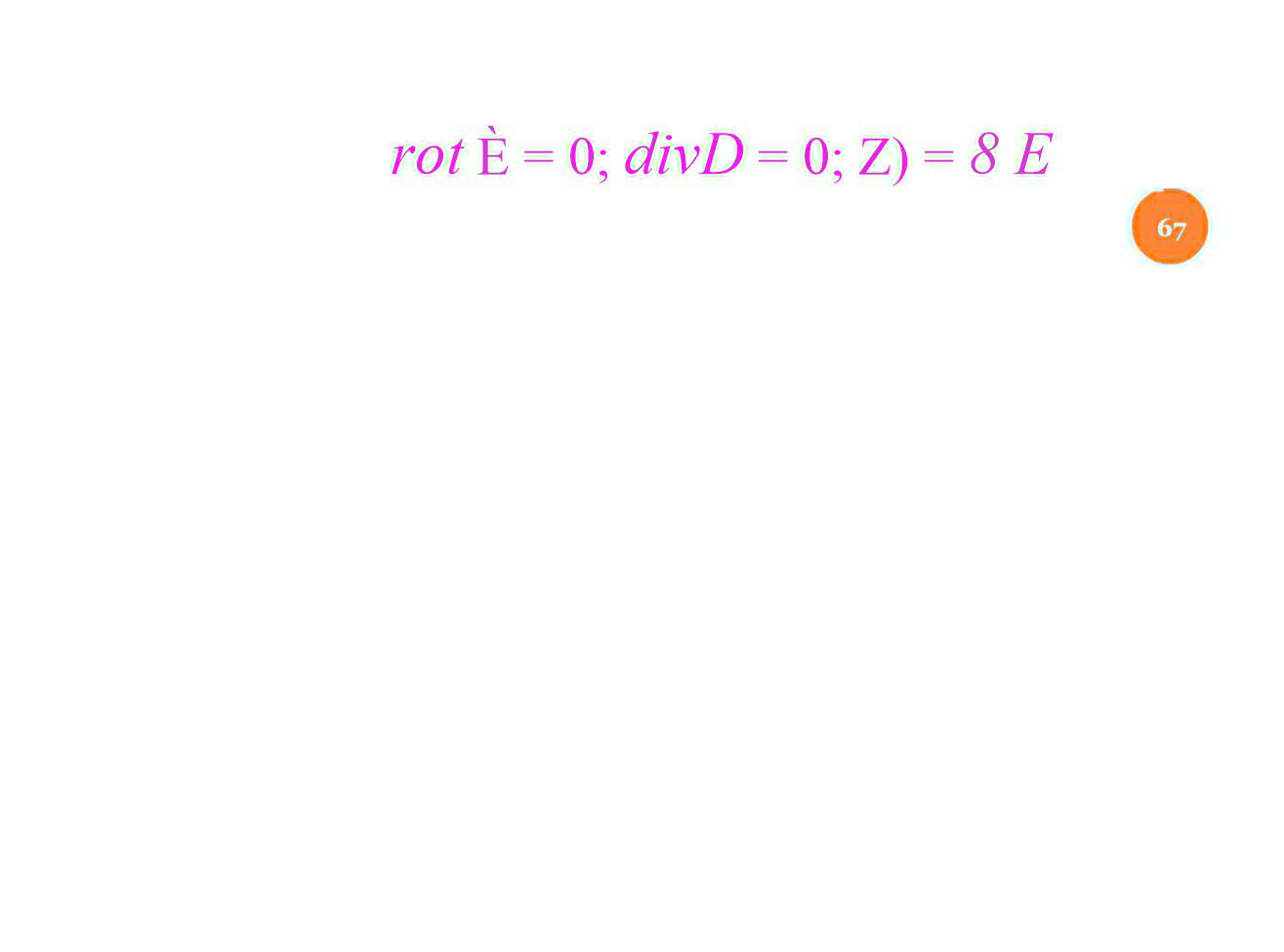
Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Trường điện từ - Chương 3: Trường điện từ dừng - Nguyễn Thị Linh Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Trường điện từ - Chương 3: Trường điện từ dừng - Nguyễn Thị Linh Phương

CHƯƠNG 3.
TRƯỜNG ĐIỆN TỪ DỪNG
CHƯƠNG 3.
TRƯỜNG ĐIỆN TỪ DỪNG
Chia thành 2 nhóm : Trường từ dừng & trường điện dừng
o Trường từ dừng gây bởi dòng điện dẫn không đổi
theo thời gian. 77 7 /. 7; /v 7; 77
6 rot H = J\divB = 0'8 = ụH
o Trường điện dừng trong môi trường dần có dòng điện không đôi. rot g _ 0. divj = 0. J = y£
o Trường điện dừng trong điện môi lý tưởng.
rot È = 0; divD = 0; Z) = 8 E
Điện trở
Môi trương 1 là môi trường vật dẫn mang dòng điện không đổi
Môi trường 2 là điện môi lý tưởng (y = 0)
o Hệ phương trình Maxwell cho Trường từ dừng:
rotH = J divB = 0
B = /jH divJ = 0 o Diều kiện biên:
' B^S) = B.JS}
nxịT2(S)-nxHỉ(S) = Jx
The từ vô hướng (pin:
Ớ miền không có dòng điện: rotH = 0
ểZz’v5 = 0
Có thể biếu diễn H = -grad(pm
B.
(PmA~(PmB = \Hdỉ (pmM= ịHdỉ ợ>(Mo)=O
■4 M
<PmM = J HdJ+ki
mlmu
=>Thê từ vô hướng có thê không đơn tộ.
Phương trình Laplace đôi với thê từ vô hướng: o Xét miền không có dòng điện dần, p=const:
dỉvH — div(—) — 0
= 0
. = -grad(pm
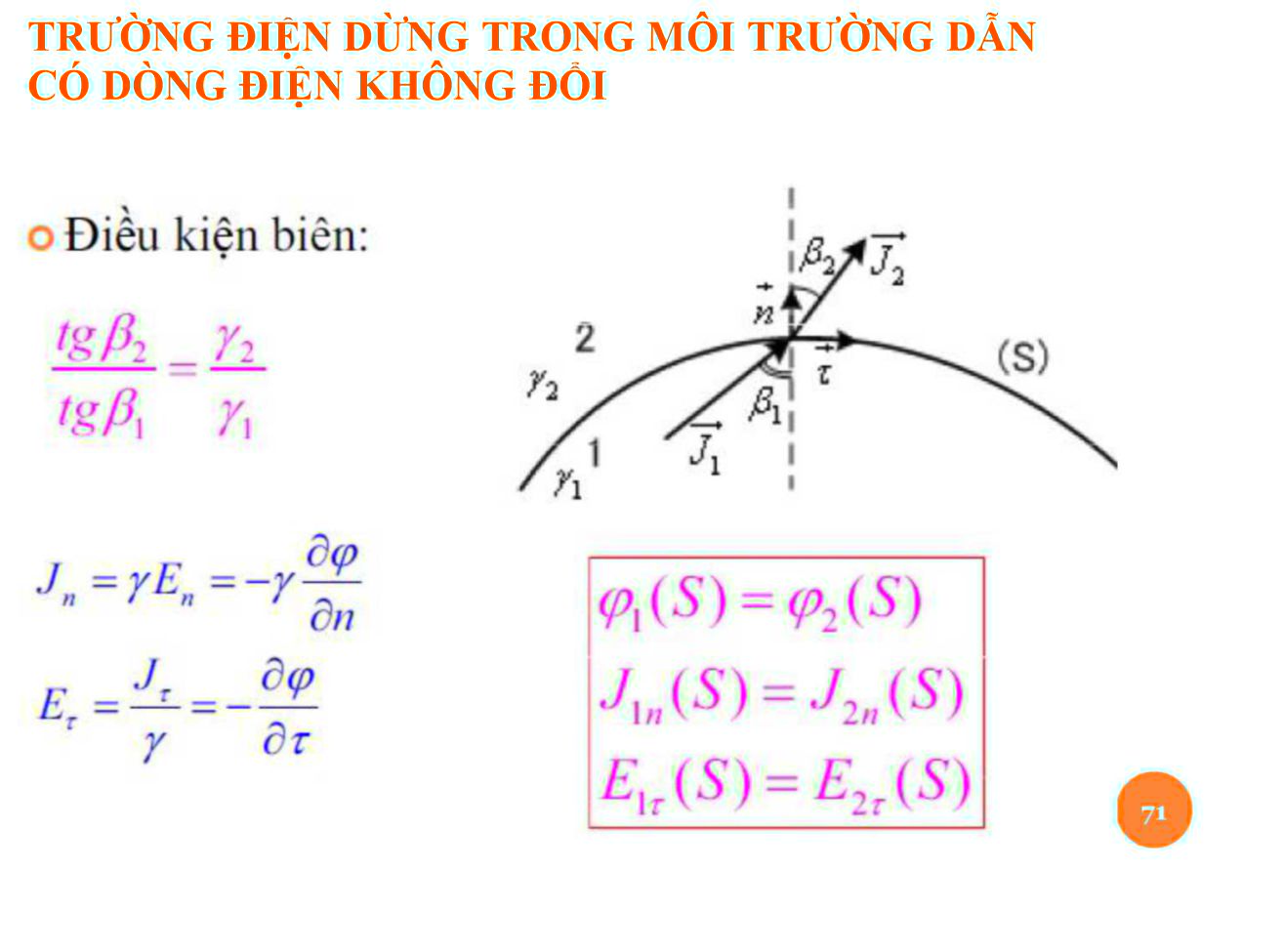
Diều kiện biên:
oTrên mặt phân cách hai mòi trường có độ thấm từ P|,p, không có mật độ dòng điện mặt.
Z?„(S) = S2,,(S)
//,,($) = /Ỹ2r(S)
B = fiH =
on
o Thế vector?!:
• Trong miền có dòng điện J#:0. không thề biểu diễn trường từ qua thê vò hướng (pni
divB = 0 — —
B = rot A
divrotA = 0 —
/Ị: the vector
A 1 = A + grudf f: hàm vô hưởng bất kỳ
rotA ’ = rot A + rotgradf = rot A
rhe vector không đơn trị Điêu kiện phụ: div A = 0
o Phương trinh Laplace đối với thế vector A :
Đinh nghĩa: A A = - ro tro í A + graddi vA
divà - 0
rotB — ro tro í A — ị{j
=> AA — —ịiJ Phương trình Poisson
J — 0 => A A = 0 Phương trình Laplace
Trong HTĐ Descartes:
A/Ịv = -ịẳJx ; AA = -ịẳJ ; = -ỊjJ=
> Nghiệm A của phương trình Laplace - Poisson trong
Xét trường từ dừng gây ra bới dòng điện dẫn chảy theo 1 phương nhất định J = J (x, ỳ} ì_
Trường từ không phụ thuộc vào tọa độ z, thế vector A song song với trục z;5, H vuông góc với trục z
A = A(x, y)ỉ ; B = rotA = gradA X /■_
Môi trường p=const, thế/í thóa pt Poisson-Laplace:
Các điêu kiện biên hôn hợp:
o Xét 2 môi trường phân cách bới mặt trụ (S), vector pháp
tuyên hướng từ mòi trường I sang môi trường 2
Năng lượng trường từ dừng tính qua thê vector A, J:
w., = ” M
BHdV = ^~ \mtAIIdV=~ i ArotHdV +ị i
2 J 2 J 2 .7
“ tbkg tbkg tbkg
Wu = T ÍÃÃdl' + ị ổ (1X 77 )dK
div(A* H)dv
r s
• Bên ngoài V. J = 0 nên sô hạng thứ nhât chi cân lây miên tích phân theo V. sổ hạng thứ 2 sẽ tiến tới 0 khi S->00
* div(ÃX 77) = TĩrotÃ- ArotTỉ
o Biếu diễn năng lượng trường từ qua từ thông, hệ số tự
cảm, hệ số hỗ cảm: I " «
i=l /=1
Mkl: hệ số hỗ cam của vòng dây thứ 1 đối với vòng dây thử k
hệ số tự cảm của vòng dây thứ 1
V
o Lực từ tác dụng lên vòng dây dẫn:
F = (ịụd!xB)
C
o Lực toàn phần tác dụng lên mặt vật dẫn mang điện:
ơ
F = Z-dS
£
BÀI TẬP CHƯƠNG 3 o 3.3; 3.4; 3.10;
3.11; 3.12
File đính kèm:
 bai_giang_truong_dien_tu_chuong_3_truong_dien_tu_dung_nguyen.docx
bai_giang_truong_dien_tu_chuong_3_truong_dien_tu_dung_nguyen.docx bai-giang-truong-dien-tu-chuong-3-ths.-nguyen-thi-linh-phuon_SID12_PID1449664.pdf
bai-giang-truong-dien-tu-chuong-3-ths.-nguyen-thi-linh-phuon_SID12_PID1449664.pdf

