Về một thuật toán lập trình trong phân tích bài toán siêu tĩnh dầm chịu uốn

 ISSN 2354-0575
 VỀ MỘT THUẬT TOÁN LẬP TRÌNH
 TRONG PHÂN TÍCH BÀI TOÁN SIÊU TĨNH DẦM CHỊU UỐN
 Khổng Doãn Điền, Nguyễn Văn Huyến, Nguyễn Duy Chinh
 Trường Đại học Sư phạm Kỹ thuật Hưng Yên
 Ngày nhận: 10/12/2016
 Ngày sửa chữa: 20/01/2017
 Ngày xét duyệt: 05/03/2017
Tóm tắt:
 Trong sức bền vật liệu, bài toán về các kết cấu siêu tĩnh là một bài toán khó, đặc biệt sẽ rất phức tạp 
nếu bậc siêu tĩnh của kết cấu lớn. Trong bối cảnh từ lần thi thứ XXIX năm 2017, ban tổ chức Olympic Cơ 
học Toàn quốc chính thức đưa vào môn thi Ứng dụng tin học trong Sức bền vật liệu, lập trình trên nền phần 
mềm Maple, vì vậy việc nghiên cứu các thuật toán giải các bài toán sức bền vật liệu nói chung và lớp các 
bài toán về các kết cấu siêu tĩnh nói riêng là một vấn đề hết sức quan trọng và ý nghĩa. Bài báo này trình 
bày một thuật toán giải bài toán dầm siêu tĩnh chịu uốn có số bậc siêu tĩnh lớn. Các kết quả tính toán và 
mô phỏng được lập trình trên phần mềm Maple 2016 và so sánh với các công bố của Hội Cơ học Việt Nam 
[4] cho kết quả chính xác và tin cậy.
Từ khóa: Sức bền vật liệu, dầm, kết cấu siêu tĩnh, bậc siêu tĩnh.
1. Đặt vấn đề học phần Sức bền vật liệu truyền thống và được 
 Kết cấu siêu tĩnh [1,2] trong thực tế được cung cấp kiến thức lập trình, tư duy toán học, xử 
sử dụng rất rộng rãi do tính ưu việt của nó đó là độ lý thuật toán. Với mục đích ứng dụng công nghệ 
cứng vững của kết cấu rất cao. Hầu hết các kết cấu thông tin trong tính toán, để đơn giản hóa những bài 
trong thực tế đều là các kết cấu siêu tĩnh, có bậc toán phức tạp, những kết cấu siêu tĩnh bậc cao, mà 
siêu tĩnh lớn [5], chẳng hạn như cầu, mái vòm sân không làm mất đi cái hồn của thuật toán (cái hồn 
vận động, kết cấu khung nhà thép, giàn khoan, nhà của phương pháp giải [3]), Ban tổ chức chính thức 
giàn trên biển, Tuy có tính ưu việt trong thực tế chọn phần mềm toán học Maple để xây dựng một 
kỹ thuật, nhưng trong tính toán đặc biệt là các tính người sinh viên kỹ thuật hoàn thiện đầy đủ về các 
toán tối ưu, việc giải các bài toán siêu tĩnh không mặt Toán, Tin, Cơ.
phải đơn giản, và có thể không khả thi trong trường Bài báo này trình bày một thuật toán giải bài 
hợp kết cấu có bậc siêu tĩnh rất lớn. toán dầm siêu tĩnh chịu uốn có số bậc siêu tĩnh lớn. 
 Ngày nay, với sự phát triển của công nghệ Các kết quả tính toán và mô phỏng được lập trình 
thông tin, rất nhiều phần mềm toán học, cơ học ra trên phần mềm Maple 2016 và so sánh với các công 
đời để hỗ trợ các nhà kỹ thuật trong tính toán kết bố của Hội Cơ học Việt Nam [4] cho kết quả chính 
cấu. Với việc sử dụng các phương pháp mạnh như xác và tin cậy.
phương pháp phần tử hữu hạn (FEM), phương pháp 
dội sóng ngược (RAY), việc giải các kết cấu siêu 2. Cơ sở lý thuyết [2,5]
tĩnh trở nên đơn giản hơn. Một số phần mềm kinh Để giải được các kết cấu siêu tĩnh nói chung 
điển có thể kể đến ở đây như phần mềm phân tích và đặc biệt là các kết cấu siêu tĩnh có bậc siêu tĩnh 
kết cấu SAP2000, INVENTOR, CATIA, ABAQUS lớn đối với lớp các bài toán dầm chịu uốn thì việc 
 Tuy nhiên, xét về mặt học thuật việc sử dụng các xây dựng các hàm độ võng, góc xoay, hàm mô tả 
phần mềm này tuy mang lại nhiều hiệu quả, nhưng mô men uốn và lực cắt trong dầm phụ thuộc vào vị 
với sinh viên, người nghiên cứu thì nó làm mất đi trí mặt cắt là việc làm chính yếu. Bài báo trình bày 
tính tư duy, kiến thức nền tảng của người học, vì thuật toán cải tiến dựa trên nền phương pháp kinh 
đơn thuần người sử dụng chỉ cần biết vào/ra dữ liệu điển thông số ban đầu. Dạng biểu diễn tổng của hàm 
là đủ, mà không hình dung được quá trình tính toán độ võng, góc xoay, mô men uốn và lực cắt trong 
diễn ra như thế nào. Từ đó không thể có những can dầm chịu uốn lần lượt được biểu diễn như sau:
thiệp, cải tiến sâu hơn về mặt thuật toán để có thể 
 J * U2 N
 KDUyM00ii++DUz01 0i +O
giải quyết được các kết cấu mới, lớp các bài toán K EJ O
 n K O
mới mà các phần mềm kể trên chưa cập nhật. K U3 U4 O
 yz()= / K++P0iiDq0 + O (1)
 Trong bối cảnh, từ năm 2017, Ban Tổ chức i = 1 K EJ EJ O
 K O
Olympic Cơ học Toàn quốc chính thức đưa vào môn K ,,UU5 , 6 O
 K++q0iiq0 + ... O
thi thứ 11. Lấy ý tưởng từ việc sinh viên được học L EJ EJ P
Khoa học & Công nghệ - Số 13/Tháng 3 - 2017 Journal of Science and Technology 9
ISSN 2354-0575
 ,,,
 dy()z Dqq0i ,,00iiq .... bước nhảy của hàm và các đạo hàm 
 { ()z =
 dz (2) các cấp của q tại đầu trái đoạn i.
 n *
 Mz()= / MP00iiUU++01DUq02i + (3)
 i = 1 ,,, 3. Thuật giải lập trình và kết quả
 eo+qq0iiUU3 ++0 4 ...
 Để minh chứng cho sức mạnh của thuật toán, 
 dM()z các tác giả khảo sát và nghiên cứu dầm siêu tĩnh bậc 
 Qz()= (4)
 dz 4 có sơ đồ như Hình 1 [4]. 
trong đó hàm vị trí được biểu diễn Dầm có độ cứng EJ không đổi, bỏ qua trọng 
 k
 ()za- i-1 lượng bản thân của dầm. Cho a = 1m, q = 50N/cm, 
 $ i-1 7 2
 Ukiza- -1 = za (5) EJ = 32.10 Ncm
 ^h k !
 * 00##zai-1 Thực hiện các công việc sau :
i là tên đoạn dầm khảo sát 1. Tính các phản lực liên kết ?
oi là đầu trái của đoạn i có tọa độ ai-1 2. Vẽ biểu đồ chuyển vị của các mặt cắt 
ai-1 là khoảng cách từ đầu trái của dầm đến mặt cắt ngang dầm ?
phân chia giữa đoạn (i-1) và đoạn i 3. Xác định giá trị lớn nhất của chuyển vị và 
EJ là độ cứng của các mặt cắt ngang dầm vị trí mặt cắt ngang tương ứng ?
 DDy00ii, { lần lượt là bước nhảy của độ võng và 4. Vẽ biểu đồ nội lực của dầm ?
góc xoay tại đầu trái đoạn i 5. Tính ứng suất tương đương và vị trí mặt 
 *
 MP0i , 0i mô men ngoại lực và lực tập trung tại đầu cắt ngang tương ứng có ứng suất tương đương lớn 
trái đoạn i nhất (mặt cắt nguy hiểm nhất) ?
 Hình 1. Kết cấu dầm 4 bậc siêu tĩnh
 Số bậc siêu tĩnh của hệ bằng 4, với số bậc Maple 2016 ta thu được các kết quả như sau:
siêu tĩnh lớn việc giải bằng các phương pháp truyền Các hàm vị trí :
thống chẳng hạn như phương pháp lực, phương pháp 1 2 1 3
 UU12= za- 3 ; = za- 3 ;U3 = za- 3
năng lượng, phương pháp nhân biểu đồ Vêrêshagin 2 ^^hh6
là không khả thi vì quá phức tạp. Bằng một chương 1 4 1 5
 UU4 = za- 3 ; 5 = za- 3
trình máy tính được lập trình trên nền phần mềm 24 ^^hh120
 Hàm lực cắt trên từng đoạn dầm:
 ]ZRA 0 ##z and zl
 ]
 ]RA + RB --qz ll##z and zl2
 [ ^ h
 ]RA + RB --qz lR++Cqzl- 22lz##and zl3
 ] ^^hh
 ]RA + RB --qz lR++Cqzl--2 Potherwise
 \ ^^hh
 Hàm mô men uốn trên từng đoạn dầm:
 ]ZRA zM+ Az0 ##and zl
 ]
 ] 1 2
 ]RA zM++ARBz--lqzl- lz##and zl2
 ] ^^hh2
 [ 1 221
 ]RA zM++ARBz--lqzl--Ms + RC zl- 2 + qz- 22ll##z and zl3
 ] ^^hh2 ^^hh2
 ]
 ] 22
 ] --1 -- - 1 ---
 ]RA zM++ARBz lq2 zl Ms + RC zl2 + 2 qz 23lPzl otherwise
 \ ^^hh ^^hh^ h
10 Khoa học & Công nghệ - Số 13/Tháng 3 - 2017 Journal of Science and Technology
 ISSN 2354-0575
 Hàm độ võng trên từng đoạn dầm:
 23
 ]Z 1 MAz 1 RAz
 ] + 0 ##z and zl
 ] 2 EJ 6 EJ
 ] 23 3 4
 ] 1 MAz 1 RAz 1 RB zl- 1 qz- l
 ] ++ - ^ h lz##and zl2
 ] 2 EJ 6 EJ 6 ^EJ h 24 EJ
 [ 23 3 4 234
 ] 1 MAz 1 RAz 1 RB zl- 1 qz- l 1 Ms zl- 2 1 RC zl- 2 1 qz- 2l
 ] ++^ h - ^ h - ^^hh+ + ^ h 23lz##and zl
 ] 2 EJ 6 EJ 6 EJ 24 EJ 2 EJ 6 EJ 24 EJ
 ] 23 3 4 234 3
 ] 1 MAz 1 RAz 1 RB zl- 1 qz- l 1 Ms zl- 2 1 RC zl- 2 1 qz- 2l 1 Pz- 3l
 ] ++ - ^ h - + + ^ h - otherwise
 ] 2 EJ 6 EJ 6 ^EJ h 24 EJ 2 ^^EJ hh6 EJ 24 EJ 6 ^ EJ h
 \
 Hàm góc xoay trên từng đoạn dầm:
 2
 ]Z MAz 1 RAz
 ] + 0 ##z and zl
 ] EJ 2 EJ
 ] 2 2 3
 ] MAz 1 RAz 1 RB zl- 1 qz- l
 ] ++ - ^ h lz##and zl2
 ] EJ 2 EJ 2 ^EJ h 6 EJ
 [ 2 2 3 2 3
 ] MAz 1 RAz 1 RB zl- 1 qz- l Ms zl- 2 1 RC zl- 2 1 qz- 2l
 ] ++^ h - ^ h - ^^hh+ + ^ h 23lz##and zl
 ] EJ 2 EJ 2 EJ 6 EJ EJ 2 EJ 6 EJ
 ] 2 2 3 2 3 2
 ] MAz 1 RAz 1 RB zl- 1 qz- l Ms zl- 2 1 RC zl- 2 1 qz- 2l 1 Pz- 3l
 ] ++ - ^ h - + + ^ h - otherwise
 ] EJ 2 EJ 2 ^EJ h 6 EJ ^^EJ hh2 EJ 6 EJ 2 ^ EJ h
 \
 Sau khi đã thiết lập được các hàm nội lực và biên về chuyển vị tại các vị trí liên kết và kết hợp 
hàm chuyển vị trong dầm siêu tĩnh trên, để xác định với các phương trình cân bằng:
được các phản lực liên kết, ta sử dụng các điều kiện 
pt1 := subs(z = 1, y[1]) = 0;
 23
 1 MA l +=1 RA l
 2 EJ 6 EJ 0
pt2 := subs(z = 2 $ l, y[2]) = 0;
 233 ql4
 2 MA l ++4 RA l 1 RB l -=1
 EJ 3 EJ 6 EJ 24 EJ 0
pt3 := subs(z = 4 $ l, y[4]) = 0;
 233 ql4 233
 8 MA l ++32 RA l 9 RB l --65 2 Ms l +-4 RC l 1 Pl =
 EJ 3 EJ 2 EJ 24 EJ EJ 3 EJ 6 EJ 0
pt4 := subs(z = 4 $ l, {[]4 ) = 0;
 22ql3 22
 48MA l ++RA l 9 RB l --19 22Ms l +-RC l 1 Pl =
 EJ EJ 2 EJ 6 EJ EJ EJ 2 EJ 0
ptcb1 := RA + RB + RC + RE = P + q $ l;
 RA + RB + RC + RE = l q + P
 $
 =-$$+-$ 3 l $$-+$$-+$$ =
 ptcb2:;MA RB lql 2 RC 23lMsP lREl40ME
 -+3 2 --+- +=
 MA RBl 2 ql 23RC lMsPlR40El ME ;
 Sau đó giải hệ các phương trình trên ta thu được kết quả:
 ====$$721 $$= 1 $
lq::100 ::50 EJ::32 10 Ms::6 qlPq::2 l
evalf(solve({pt1, pt2, pt3, pt4, ptcb1, ptcb2}, {MA, RA, RB, RC, RE, ME}));
{MA = 17045.45455, ME = 49242.42424, RA = -511.3636364, RB = 3295.454545, RC = 3664.772727, RE 
= 1051.136364}
assign(%);
 Từ đó các hàm nội lực và chuyển vị trong vị trong dầm siêu tĩnh thu được lần lượt như sau:
dầm hoàn toàn xác định. Biểu đồ nội lực và chuyển 
Khoa học & Công nghệ - Số 13/Tháng 3 - 2017 Journal of Science and Technology 11
ISSN 2354-0575
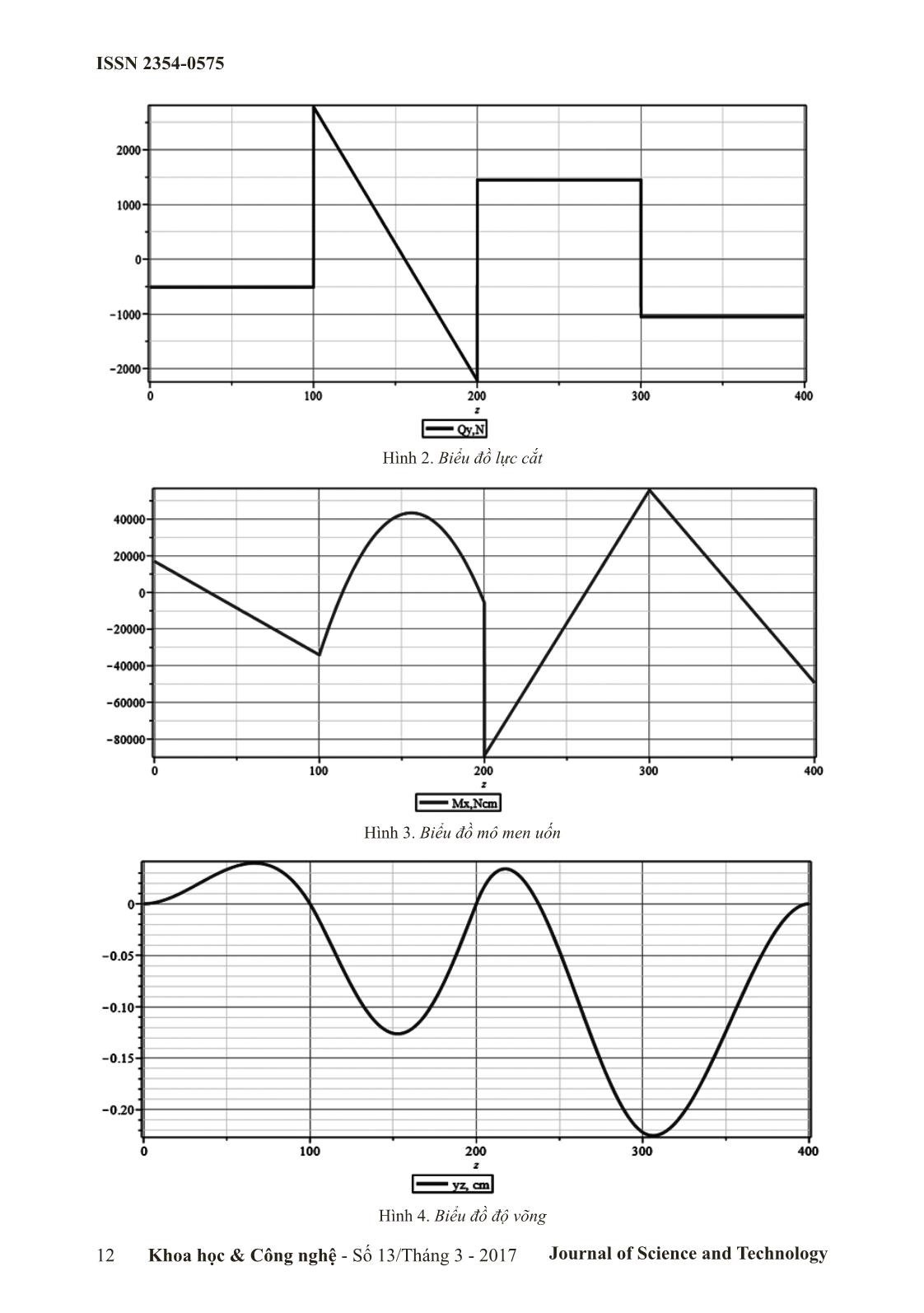
 Hình 2. Biểu đồ lực cắt
 Hình 3. Biểu đồ mô men uốn
 Hình 4. Biểu đồ độ võng
12 Khoa học & Công nghệ - Số 13/Tháng 3 - 2017 Journal of Science and Technology
 ISSN 2354-0575
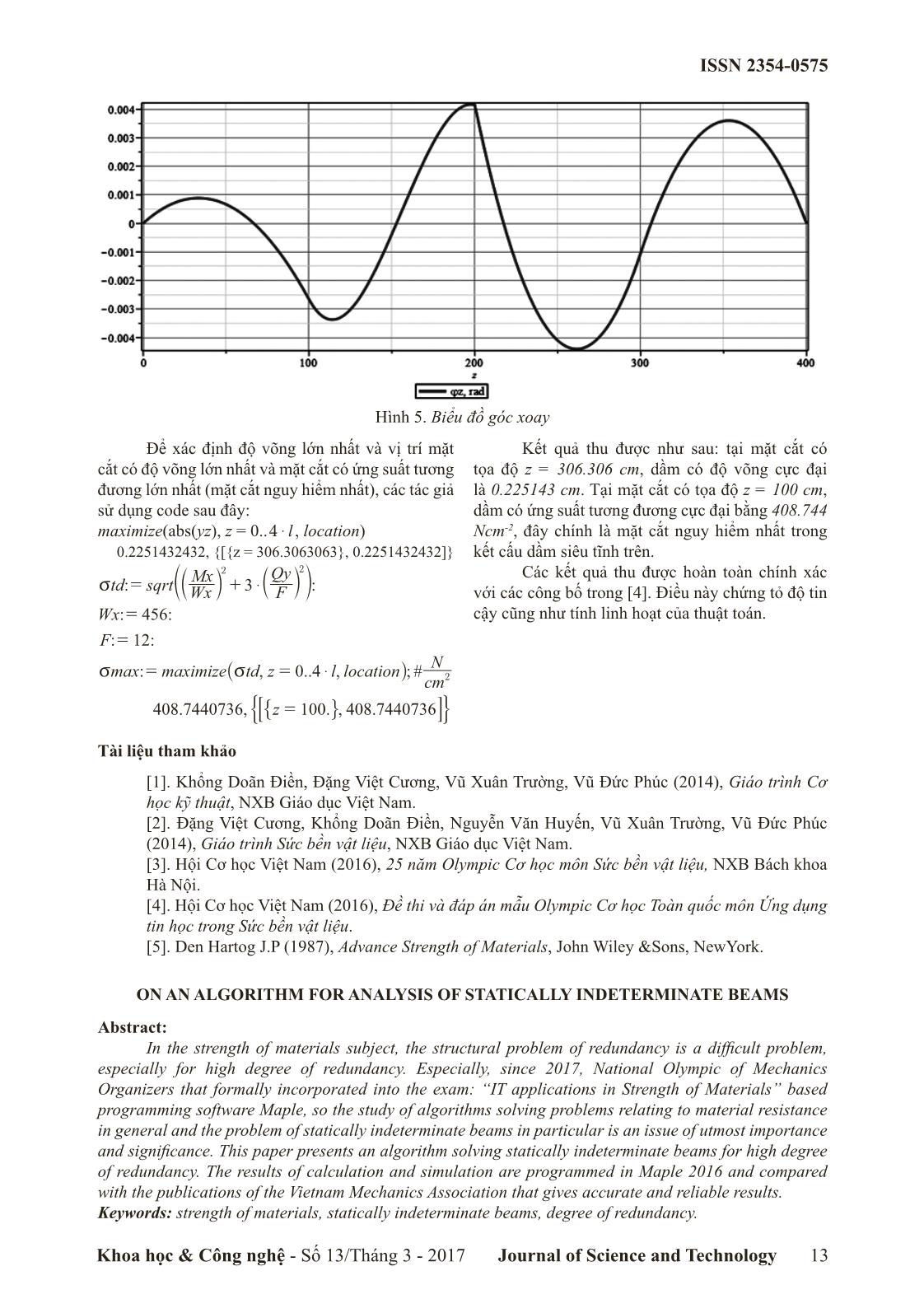
 Hình 5. Biểu đồ góc xoay
 Để xác định độ võng lớn nhất và vị trí mặt Kết quả thu được như sau: tại mặt cắt có 
cắt có độ võng lớn nhất và mặt cắt có ứng suất tương tọa độ z = 306.306 cm, dầm có độ võng cực đại 
đương lớn nhất (mặt cắt nguy hiểm nhất), các tác giả là 0.225143 cm. Tại mặt cắt có tọa độ z = 100 cm, 
sử dụng code sau đây: dầm có ứng suất tương đương cực đại bằng 408.744 
maximize(abs(yz), z = 0..4 $ l, location) Ncm-2, đây chính là mặt cắt nguy hiểm nhất trong 
 0.2251432432, {[{z = 306.3063063}, 0.2251432432]} kết cấu dầm siêu tĩnh trên.
 2
 Mx 2 Qy Các kết quả thu được hoàn toàn chính xác 
vtd::=+sqrt 3 $
 dbWx l b F l n với các công bố trong [4]. Điều này chứng tỏ độ tin 
Wx::= 456 cậy cũng như tính linh hoạt của thuật toán.
 F::= 12
 N
vvmaxm:,==aximizetdz 04.. $ ll,;ocation #
 _ i cm2
 408.,7440736 z = 100.,408.7440736
 %8B# - /
Tài liệu tham khảo
 [1]. Khổng Doãn Điền, Đặng Việt Cương, Vũ Xuân Trường, Vũ Đức Phúc (2014), Giáo trình Cơ 
 học kỹ thuật, NXB Giáo dục Việt Nam.
 [2]. Đặng Việt Cương, Khổng Doãn Điền, Nguyễn Văn Huyến, Vũ Xuân Trường, Vũ Đức Phúc 
 (2014), Giáo trình Sức bền vật liệu, NXB Giáo dục Việt Nam.
 [3]. Hội Cơ học Việt Nam (2016), 25 năm Olympic Cơ học môn Sức bền vật liệu, NXB Bách khoa 
 Hà Nội.
 [4]. Hội Cơ học Việt Nam (2016), Đề thi và đáp án mẫu Olympic Cơ học Toàn quốc môn Ứng dụng 
 tin học trong Sức bền vật liệu.
 [5]. Den Hartog J.P (1987), Advance Strength of Materials, John Wiley &Sons, NewYork.
 ON AN ALGORITHM FOR ANALYSIS OF STATICALLY INDETERMINATE BEAMS
Abstract:
 In the strength of materials subject, the structural problem of redundancy is a difficult problem, 
especially for high degree of redundancy. Especially, since 2017, National Olympic of Mechanics 
Organizers that formally incorporated into the exam: “IT applications in Strength of Materials” based 
programming software Maple, so the study of algorithms solving problems relating to material resistance 
in general and the problem of statically indeterminate beams in particular is an issue of utmost importance 
and significance. This paper presents an algorithm solving statically indeterminate beams for high degree 
of redundancy. The results of calculation and simulation are programmed in Maple 2016 and compared 
with the publications of the Vietnam Mechanics Association that gives accurate and reliable results.
Keywords: strength of materials, statically indeterminate beams, degree of redundancy.
Khoa học & Công nghệ - Số 13/Tháng 3 - 2017 Journal of Science and Technology 13