Phát triển chương trình con làm khớp dữ liệu với nhiều mô hình

TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 03 - 2016 ISSN 2354-1482 
122 
PHÁT TRIỂN CHƯƠNG TRÌNH CON LÀM KHỚP DỮ LIỆU 
VỚI NHIỀU MÔ HÌNH 
ThS. Nguyễn Ngọc Anh1 
ThS. Trương Văn Minh2 
TÓM TẮT 
Hiện nay, có rất nhiều phần mềm máy tính cho phép người dùng làm khớp dữ 
liệu thực nghiệm với dạng hàm tùy ý nhập bởi người dùng. Tuy nhiên, các chương 
trình này có dạng đóng (đối với các chương trình thương mại) hoặc có hệ thống thư 
viện liên kết rất phức tạp (đối với các chương trình mã nguồn mở). Do đó, việc tận 
dụng thư viện của các chương trình này để nhúng vào các chương trình phần mềm 
nhỏ tự thiết kế là không thích hợp. Bài báo này đưa ra bộ chương trình con, cho 
phép người dùng làm khớp số liệu thực nghiệm với dạng hàm tùy ý, được viết bằng 
ngôn ngữ C++, có cấu trúc đơn giản, gói gọn trong một tập tin chỉ dài 438 dòng, 
thuận tiện để nhúng vào các chương trình tự phát triển. Kết quả thu được bằng 
chương trình được so sánh với ROOT. 
Từ khóa:Chương trình làm khớp nền C++, thuật toán làm khớp Levenberg–
Marquardt
1. Giới thiệu 
Làm khớp dữ liệu theo một mô 
hình (dạng hàm) là một thủ tục được tiến 
hành rất phổ biến trong phân tích số liệu 
(phân tích phổ, xây dựng mô hình, xác 
định các tham số để nội suy, ngoại suy). 
Các thủ tục này có thể được thực hiện bởi 
các chương trình có giao diện trực quan 
như Origin [1], SciDavis [2] hoặc các 
chương trình dưới dạng lệnh thực thi như 
ROOT [3], R [4], Matlab [5], Gnuplot 
[6]. Tuy nhiên, một số là các chương 
trình thương mại (Origin, Matlab), do đó 
người sử dụng sẽ phải bỏ ra một chi phí 
không nhỏ để trang bị phần mềm. Tiếp 
nữa, các chương trình này thường có bộ 
thư viện đi kèm rất lớn, và liên kết với 
nhau rất phức tạp. Do, đó việc nhúng các 
thư viện này vào các chương trình nhỏ tự 
viết là rất phức tạp, và làm tăng kích 
thước của chương trình. 
Trong thực tế, tùy thuộc vào tình 
huống cụ thể, việc sử dụng các phần 
mềm lớn kể trên để làm khớp không 
phải lúc nào cũng thuận lợi: chương 
trình quá nặng; hệ điều hành không hỗ 
trợ;  Khi đó các phần mềm tự viết sẽ 
là một giải pháp thích hợp. 
Bộ chương trình con được cung 
cấp trong bài báo này cho phép người 
dùng nhúng vào trong các phần mềm tự 
viết, để thực thi tác vụ làm khớp số liệu 
theo mô hình bất kỳ do người dùng khai 
báo, sử dụng thuật toán LEVENBERG-
MARQUARDT [7]. Chương trình cho 
phép người dùng lựa chọn làm khớp có 
trọng số hoặc không có trọng số. Bộ 
chương trình con này có kích thước rất 
nhỏ, chỉ ~12 kb, gói gọn trong một tập 
tin *.h, thuận tiện để người dùng khai 
báo trong chương trình chính. Ngôn 
ngữ được sử dụng là C++.Biên dịch 
bằng GNU g++ [8]. 
Bộ chương trình con được hiệu 
lực hóa bằng cách so sánh kết quả với 
chương trình mã nguồn mở đã được 
chứng nhận và sử dụng rộng rãi trên các 
phòng thí nghiệm trên thế giới, 
ROOT.Trong báo cáo này, bộ số liệu 
đã được sử dụng để so sánh. 
1
Viện Nghiên cứu Hạt nhân Đà Lạt 
2
 Trường Đại học Đồng Nai 
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 03 - 2016 ISSN 2354-1482 
123 
2. Thuật toán v s 
 tr 
Thuật toán LEVENBERG-
MARQUARDT 
Xét bộ số liệu với n điểm thực 
nghiệm (Xi,Yi), mô hình cần làm khớp 
là F(X,α), với α là vectơ tham số 
{α1,α2,α3,.,αm). Theo đó: 
 Yi=F(Xi,α1,α2,α3,.,αm) (1) 
Để xác định các tham số tự do, 
ta sử dụng phương pháp bình phương 
tối thiểu [9]. Phương pháp này đòi hỏi 
phải xác định αsao cho là cực tiểu: 
(2) 
Trong đó là trọng số tương ứng 
với điểm số liệu thứ i. cực tiểu khi: 
(3) 
Đối với các hàm tuyến tính, hệ 
m phương trình nói trên có thể được 
giải ra nghiệm xác định bằng phương 
pháp Gauss-Jordan.Tuy nhiên, với các 
bài toán phi tuyến, hệ phương trình trên 
không thể giải được. Khai triển F(X,α) 
theo chuỗi Taylor, ta thu được biểu thức 
dưới dạng ma trận: 
(4) 
Trong đó M là ma trận [m m] mà: 
(5
) 
Và 
(6
) 
là vectơ biến thiên của vectơ 
tham số . 
Giải phương trình (3) cho phép 
xác định , từ đó xác định được 
mới. Thủ tục này lặp đi lặp lại nhiều lần 
cho tới khi hội tụ. Phương pháp 
LEVENBERG-MARQUARDT, bổ 
sung thêm vào thuật toán 2 tham số và 
, nhằm cải thiện khả năng hội tụ của 
quá trình khớp. 
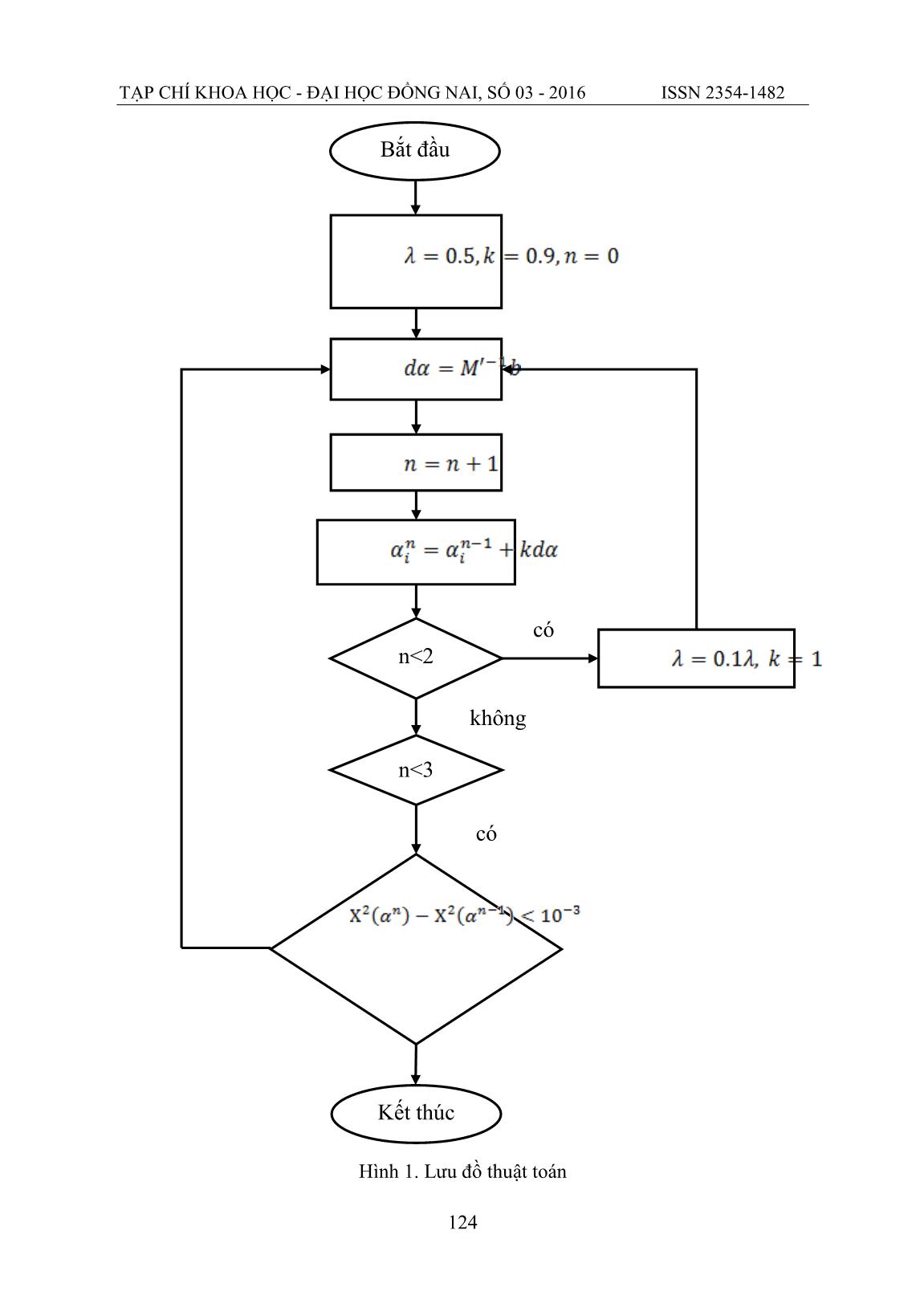
Thuật toán có thể được mô tả 
ngắn gọn, từng bước một như sau, lưu 
đồ thuật toán được đưa ra trong Hình 1: 
1. Đặt , , n=0. 
2. Xác định từ phương trình: 
(7) 
Với , là ma trận 
đơn vị. 
3. n=n+1 
4. 
5. Tính 
6. Nếu n<2, đi tới bước 9 
7. Nếu n<3, đi tới bước 8 
8. Nếu , 
trong đó thì tiếp tục 
vòng lặp, nếu không, thoát ra 
khỏi vòng lặp. 
9. Đặt ; Quay lại 
bước 2. 
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 03 - 2016 ISSN 2354-1482 
124 
Hình 1. Lưu đồ thuật toán 
 ắt đầu 
n<2 
n<3 
Kết thúc 
có 
không 
có 
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 03 - 2016 ISSN 2354-1482 
125 
S d tr o 
Thủ tục làm khớp dữ liệu được thực hiện bởi hai chương trình con LSfit_NL 
(không có trọng số) và LSfit_NLW (có trọng số). Cú pháp khai báo như sau: