Điều khiển trượt trên cơ sở bất đẳng thức ma trận tuyến tính cho hệ thống nhiều động cơ khi có yếu tố phi tuyến tác động

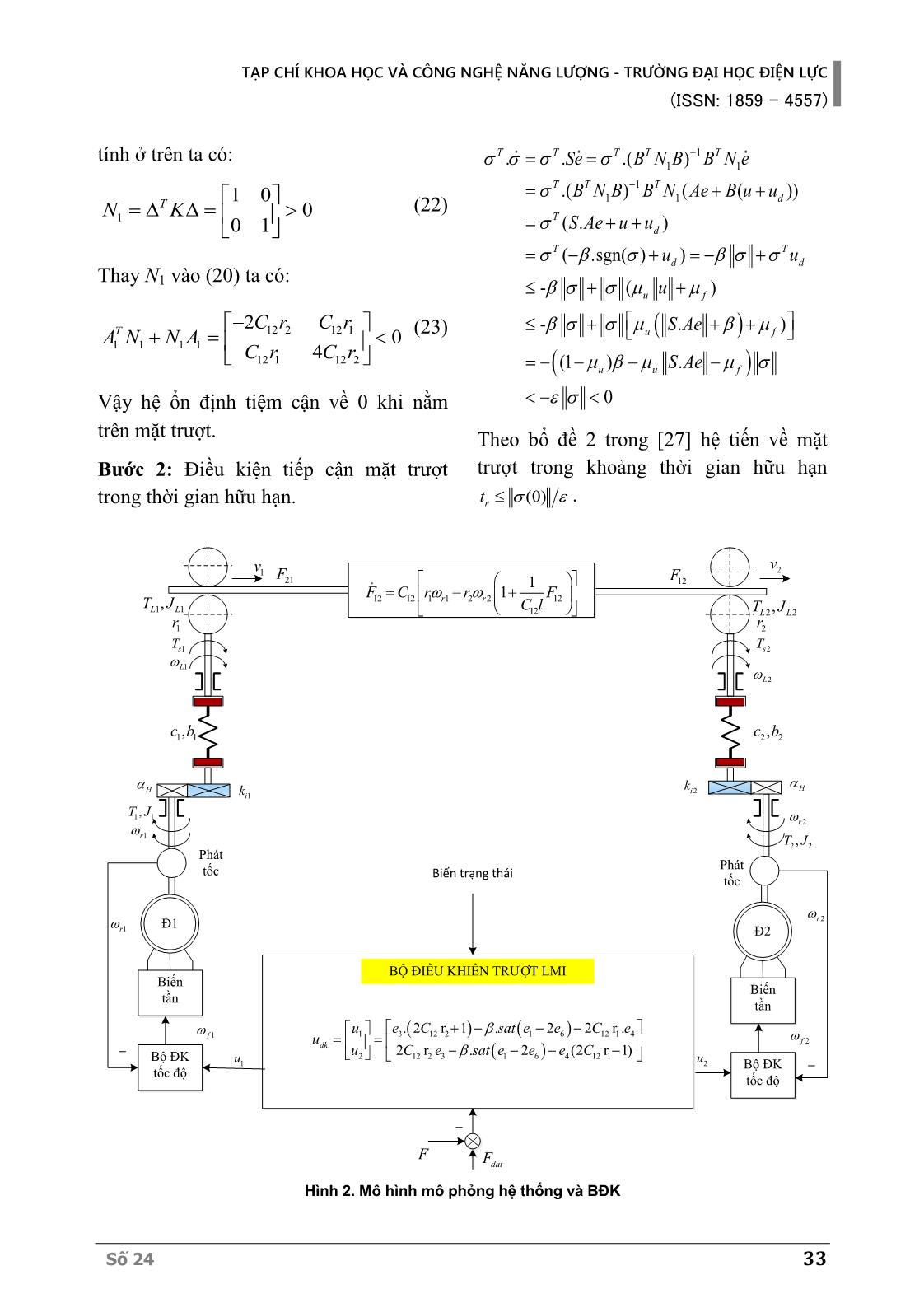
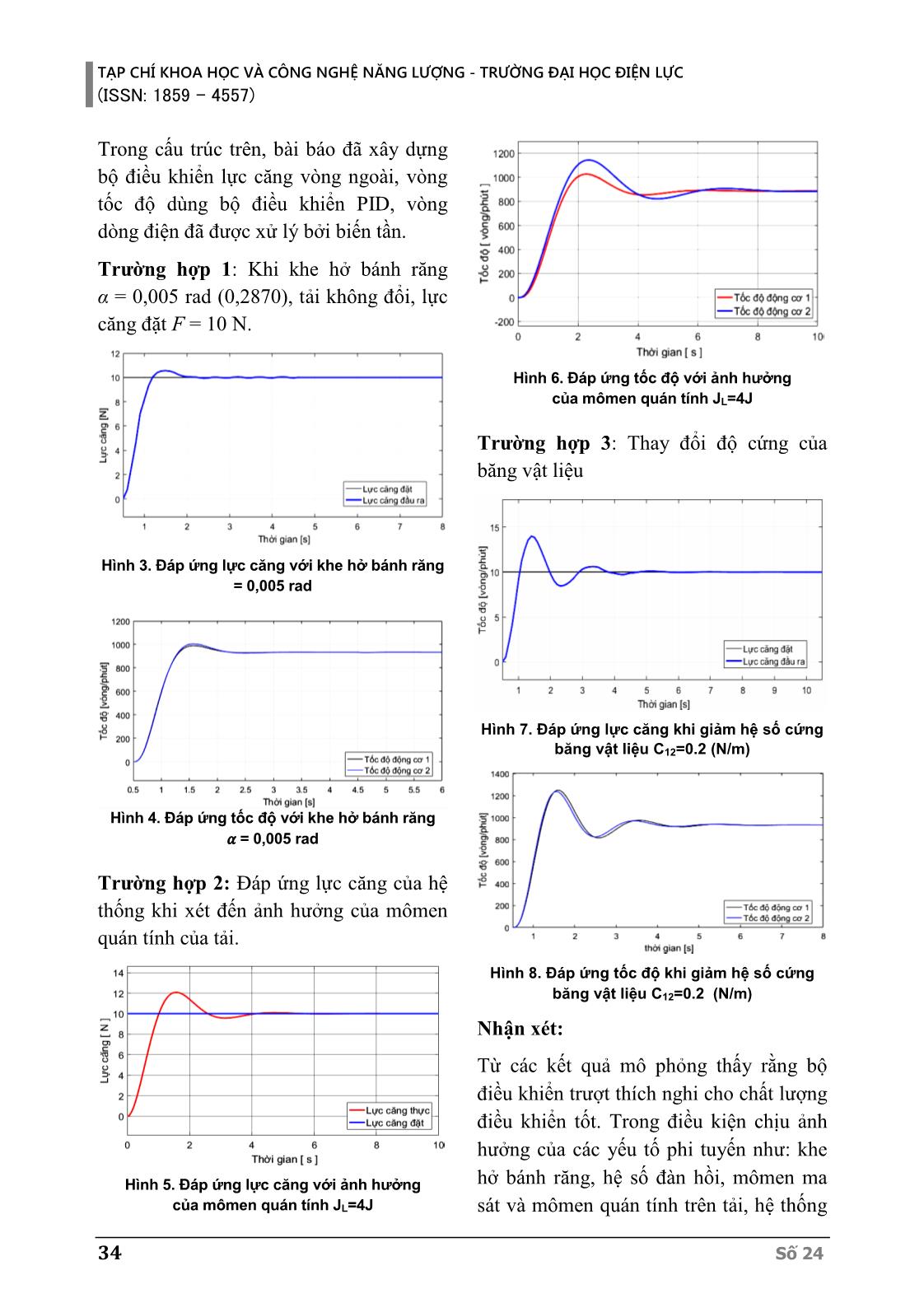
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 24 29 
ĐIỀU KHIỂN TRƯỢT TRÊN CƠ SỞ BẤT ĐẲNG THỨC MA TRẬN TUYẾN TÍNH 
CHO HỆ THỐNG NHIỀU ĐỘNG CƠ KHI CÓ YẾU TỐ PHI TUYẾN TÁC ĐỘNG 
DESIGN LINEAR MATRIX INEQUALITIES SLIDING MODE CONTROL LAW 
FOR UNCERTAIN NONLINEAR MULTI-MOTOR SYSTEMS 
 Trần Xuân Tình1*, Nguyễn Thị Linh2, Lê Văn Sâm1, Phạm Đức Trung2 
 Học viện Phòng không - Không quân1, Trường Đại học Điện lực2 
Ngày nhận bài: 23/06/2020, Ngày chấp nhận đăng: 28/12/2020, Phản biện: PGS.TS. Nguyễn Quang Hoan 
Tóm tắt: 
Bài báo trình bày kết quả tổng hợp bộ điều khiển trượt đầu cuối nhanh trên cơ sở bất đẳng thức ma 
trận cho hệ cơ điện nhiều động cơ có liên hệ ma sát, đàn hồi. Các kết quả được khảo sát đánh giá 
bằng mô phỏng trên phần mềm Matlab-Simulink cho thấy bộ điều khiển này đảm bảo được các yêu 
cầu chất lượng ngay cả khi hệ thống chịu ảnh hưởng của các yếu tố phi tuyến do cấu trúc phần cơ 
gây ra. 
Từ khóa: 
nhiều động cơ, điều khiển trượt đầu cuối, bất đẳng thức ma trận tuyến tính. 
Abstract: 
The paper presents the results of fast terminal sliding controller based on linear matrix inequality for 
many motor systems with friction, elasticity. The results surveyed and evaluated by simulation on 
Matlab-Simulink software show that the controller ensures the quality requirements in the system 
under the influence of nonlinear factors as causing the mechanical structure. 
Keywords: 
multi-motor drive systems, Adaptive Sliding mode control, elastic, backlash.
1. MỞ ĐẦU 
Hệ truyền động (HTĐ) nhiều động cơ ứng 
dụng trong công nghiệp và quốc phòng 
đều là hệ động lực học phi tuyến, chứa 
các liên hệ chéo; các mối liên hệ này làm 
cho mô hình của đối tượng điều khiển trở 
nên phi tuyến. Trong điều khiển HTĐ vật 
liệu đàn hồi nhiều động cơ, việc kiểm soát 
lực căng trên băng vật liệu là một vấn đề 
khó. Các bộ điều khiển (BĐK) HTĐ này 
liên tục được nghiên cứu phát triển từ đơn 
giản như BĐK PID [3] đến phức tạp như 
logic mờ [4], mạng nơron [5], điều khiển 
tối ưu [6], và điều khiển bền vững [7]. 
Tuy nhiên vẫn chưa có BĐK nào đáp ứng 
tốt chất lượng của hệ cũng như tính hết 
những tác động của yếu tố phi tuyến của 
phần cơ. BĐK điều khiển trượt thích nghi 
mà tác giả đề xuất đã cho chất lượng tốt 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
30 Số 24 
ngay cả khi tính đến các yếu tố phi tuyến 
như: ma sát, khe hở, đàn hồi. 
2. MÔ HÌNH CƠ HỆ 
Xét một mô hình hệ thống điện cơ hai 
khối lượng đàn hồi dạng 1 kết hợp dạng 2 
[1], [2] như hình 1. Ở đây chỉ xét dao 
động đàn hồi trong liên kết hai chiều giữa 
động cơ và tải; giữa hai tải của hai động 
cơ, các mối liên kết khác coi như cứng 
vững hoàn toàn. 
AC
F
Đ1
1 1,T J
1
1sT
1r
1 1,c b
1 1,L LT J
1r
1v
2r
2v
2 2,L LT J
AC
Đ2
2 2,T J
2
2sT
2r
2 2,c b
Hình 1. Mô hình cơ hệ đàn hồi hai động cơ 
Trong đó: T1, T2, TL1, TL2: mômen động 
cơ, tải; J1, J2, JL1, JL2: mômen quán tính 
động cơ, tải; ω1, ω2, ωr1, ωr2: tốc độ động 
cơ, tốc độ tải; c1, c2, b1, b2: hệ số cứng, hệ 
số ma sát nhớt của khớp nối, F: lực căng 
của dải vật liệu; r1, r2: bán kính rulo 1, 
rulo 2, v1, v2: tốc độ dài của dải vật liệu 
chạy qua. Chỉ số 1, 2 tương ứng của hệ 
truyền động động cơ 1 và động cơ 2. 
Trong [1, 2] tác giả đã xây dựng phương 
trình trạng thái của cơ hệ như sau: 
 
 
1 1 1 2 2 2
1 1 1 1 1 1 1 1 1 21
1
2 2 2 2 2 2 2 2 2 12
2
12 12 1 1 2 2 12
12
21 12 1 1 2 2 21
12
12
; 
1
. ( ) ( ) ( )
1
. ( ) . ( ) ( )
1
(1 )
.
1
(1 )
.
r L r L
L c b L
L
L c b L
L
L L
L L
k f k g T r F
K
k f k g T r F
K
F C r r F
C l
F C r r F
C l
y F
    
 
 
 
 
(1) 
trong đó: 
2 2
; dm dmc b
dm dm
c b
k k
i T i T
 
 là hệ số tỉ lệ 
độ cứng và ma sát của phần cơ. 
Đặt:  1 2 3 4 5 6
T
x x x x x x x 
 1 2 1 2 21 12
T
L L F F   
   1 2 1 2
T T
r ru u u   ; 
Ta được: 
 
 
1 1 3 2 2 4
3 1 1 1 1 1 1 1 1 5
1
4 2 2 2 2 2 2 2 2 6
2
5 12 1 3 2 4 5
12
6 12 1 3 2 4 6
12
; 
1
. ( ) . ( ) ( )
1
. ( ) . ( ) ( )
1
(1 )
.
1
(1 )
.
c b L
L
c b L
L
x u x x u x
x k f x k g x T r x
K
x k f x k g x T r x
K
x C r x r x x
C l
x C r x r x x
C l
(2) 
Các hàm 1 2 1 2( ), ( ), ( ), ( )f x f x g x g x là hàm phi 
tuyến phụ thuộc vào khe hở bánh răng 
hộp số. 
1
1 1 1
1 1
0 khi 
( ) khi >
 khi <-
H
H H
H H
x
f x x x
x x
; 
1 1 1( ) . ( )g x x f x ; 
với 
1
1
1
0 khi 
( )
1 khi 
H
H
x
f x
x
Đưa được mô hình (2) về dạng: 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 24 31 
 ,d
d
x Ax B u u x t
dt
(3) 
Đặt x 
ref
e x khi đó có mô hình sai 
lệch bám: 
 ,d
d
e Ae B u u e t
dt
(4) 
trong đó: 
1
1
2
2
12 1 12 2
12 1 12 2
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 . . 0 0
0 0 . . 0 0
L
L
r
K
A
r
K
C r C r
C r C r
1
2
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
0 0 0 0
0 0 0 0
L
L
K
B
K
;
1
2
0
0
r
r
u


1 1 1 1 1 1 1
2 2 2 2 2 2 2
0
0
(e, t)d
c b L
c b L
u
k f e k g e T
k f e k g e T
;
1
2
3
4
5
6
e
e
e
e
e
e
e
Đề xuất thiết kế bộ điều khiển trượt thỏa 
mãn bất đẳng thức ma trận tuyến tính 
LMI (linear matrix inequalities) có tính 
đến sự hội tụ về mặt trượt trong khoảng 
thời gian hữu hạn cho hệ truyền động 
nhiều động cơ. Lựa chọn mặt trượt và 
biến trượt được xác định như sau: 
 
1
1 1
: 0 ,n
T T
e t Se
S B K B B K

 (5) 
Với K thỏa mãn bất đẳng thức ma trận 
LMI như sau: 
 0; 0;
0 0 0 0 0 1
0 0 0 0 1 0
T T
T
AK KA K 
(6) 
Trong đó ∆ là ma trận trực giao thỏa mãn 
T I được xác định (B')null , nghĩa 
là thỏa mãn '. 0B . Với quy ước các bất 
đẳng thức ma trận có dấu < 0 là ma trận 
xác định âm còn > 0 là ma trận xác định 
dương. Đặt , 6x6= , 1,6i jK i j
 . 
Giải điều kiện bất đẳng thức ma trận LMI 
[8,9] thu được : 
12 1 53 35 2 54 45
12 1 63 45 2 35 64
12 1 36 54 2 53 46
12 2 63 35 1 64 46
T TAK KA
C r r
C r r
C r r
C r r
   
   
   
   
 (7) 
khi đó mặt trượt được cho bởi: 
1
1 1 0T TSe B K B B K e
(8) 
Trong đó biến trượt được tính như sau: 
1
1 1
1 1
2 2
1 0 0 0 0 2
0 1 0 0 0 2
0 0 0 0 2
0 0 0 0
T T
L L
L L
S B K B B K
K K
K K
(9) 
Mặt trượt khi đó được tính: 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
32 Số 24 
1
1 1
1
2
3
41 1
52 2
6
1 0 0 0 0 2
0 1 0 0 0 2
 .
0 0 0 0 2
0 0 0 0
T T
L L
L L
B K B B K e
e
e
e
eK K
eK K
e

(10) 
Một luật điều khiển trượt được thiết kế: 
 1
2
. .dk
u
u S Ae sign
u
 
(11) 
Thay S, A, σ ở trên vào (11) ta có: 
3 12 2 1 6 12 1 4
12 2 3 1 6 4 12 1
1
2
. 2 r 1 . 2 2 r .
2 r . 2 (2 r 1)
dk
u
u
e C sign e e C e
C e sign e e e C
u


(12) 
Chứng minh hệ ổn định tiệm cận với thời 
gian hữu hạn. 
Bước 1: Chứng minh hệ ổn định tiệm cận 
về 0 khi đã nằm trên mặt trượt. 
Xét ma trận biến đổi M và liên kết vectơ 
z được định nghĩa như sau: 
1
1
1 1
T T
T T
K G
M
SB K B B K
(13) 
1
2
z Ge
z M e
z Se
(14) 
Do đó, đạo hàm thời gian của z được tính 
như sau: 
1
. . . ( )
 . . ( )
d
d
z M e M Ae M B u u
M AM z M B u u 
(15) 
Sau đó, hệ thống điều khiển vòng kín 
(4) có thể là chuyển thành dạng thông 
thường sau đây: 
 1 1
. . . . . 0
. . . . .
d
z G A K G A B z
u u
S A K S A B I 
(16) 
Mặt khác, từ phương pháp điều khiển 
tương đương ta có luật điều khiển tương 
đương là: 
( ) - ( )eq du t S Ae u t 
(17) 
Bằng cách đặt 0  và thay thế u t 
bằng equ t , có thể chỉ ra rằng chế độ 
trượt bậc hai ổn định trên mặt trượt (7) thể 
hiện qua 
1
1 1 
T Tz K A K z
(18) 
Chuyển động chế độ trượt (17) sẽ ổn định 
nếu tồn tại ma trận xác định dương 
2 2
1
xN R sao cho đạo hàm theo thời gian 
của hàm Lyapunov 1 1 1 1(z , t) z
TV N z thỏa 
mãn với hệ số dương γ có: 
2
1 1 1 1 1 1 1
T TV z A N N A z z 
(19) 
trong đó 
1 12 2 12 1
1
12 1 12 2
2
=
2
T T
C r C r
A K AK
C r C r
(20) 
Ma trận dương 2 2
1
xN R được xác định 
sao cho 
1 1 1 1 0
TA N N A 
(21) 
Đặt 1
TN K trong đó K là ma trận thỏa 
mãn LMI (5), bất đẳng thức Lyapunov 
(19) đúng với 1 0
TN K , như vậy chế 
độ trượt theo thứ tự giảm bậc (18) sẽ ổn 
định tiệm cận. Từ ma trận K và ∆ ở (5) đã 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 24 33 
tính ở trên ta có: 
1
1 0
0
0 1
TN K
 (22) 
Thay N1 vào (20) ta có: 
12 2 12 1
1 1 1 1
12 1 12 2
2
0
4
T
C r C r
A N N A
C r C r
(23) 
Vậy hệ ổn định tiệm cận về 0 khi nằm 
trên mặt trượt. 
Bước 2: Điều kiện tiếp cận mặt trượt 
trong thời gian hữu hạn. 
1
1 1
1
1 1
. . .( )
.( ) ( ( ))
( . )
 ( .sgn( ) )
 - ( )
 - . )
(1 ) .
0
T T T T T
T T T
d
T
d
T T
d d
u f
u f
u u f
Se B N B B N e
B N B B N Ae B u u
S Ae u u
u u
u
S Ae
S Ae
   


     
    
     
    
 
Theo bổ đề 2 trong [27] hệ tiến về mặt 
trượt trong khoảng thời gian hữu hạn 
(0)rt   . 
Đ1
1 1,T J
1r
1sT
1L
H 
1 1,c b
1 1,L LT J
1r
1v
2r
2v
2 2,L LT J
2 2,T J
2r
2sT
2L
H 
2 2,c b
12 12 1 1 2 2 12
12
1
1r rF C r r F
C l
 
Biến 
tần
BỘ ĐIỀU KHIỂN TRƯỢT LMI
datF
Bộ ĐK 
tốc độ
Phát 
tốc
Đ2
Biến 
tần
Bộ ĐK 
tốc độ
Phát 
tốc
1r
2r
1u 2u
2f1f

1ik 2i
k
21F 12F
F
Biến trạng thái
3 12 2 1 6 12 11 4
12 2 3 1 62 4 12 1
. 2 r 1 . 2 2 r .
2 r . 2 (2 r 1)
dk
e C sat e e C e
C e sat
u
u
u e e e C


Hình 2. Mô hình mô phỏng hệ thống và BĐK 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
34 Số 24 
Trong cấu trúc trên, bài báo đã xây dựng 
bộ điều khiển lực căng vòng ngoài, vòng 
tốc độ dùng bộ điều khiển PID, vòng 
dòng điện đã được xử lý bởi biến tần. 
Trường hợp 1: Khi khe hở bánh răng 
α = 0,005 rad (0,2870), tải không đổi, lực 
căng đặt F = 10 N. 
Hình 3. Đáp ứng lực căng với khe hở bánh răng 
= 0,005 rad 
Hình 4. Đáp ứng tốc độ với khe hở bánh răng 
𝛼 = 0,005 rad 
Trường hợp 2: Đáp ứng lực căng của hệ 
thống khi xét đến ảnh hưởng của mômen 
quán tính của tải. 
Hình 5. Đáp ứng lực căng với ảnh hưởng 
của mômen quán tính JL=4J 
Hình 6. Đáp ứng tốc độ với ảnh hưởng 
của mômen quán tính JL=4J 
Trường hợp 3: Thay đổi độ cứng của 
băng vật liệu 
Hình 7. Đáp ứng lực căng khi giảm hệ số cứng 
băng vật liệu C12=0.2 (N/m) 
Hình 8. Đáp ứng tốc độ khi giảm hệ số cứng 
băng vật liệu C12=0.2 (N/m) 
Nhận xét: 
Từ các kết quả mô phỏng thấy rằng bộ 
điều khiển trượt thích nghi cho chất lượng 
điều khiển tốt. Trong điều kiện chịu ảnh 
hưởng của các yếu tố phi tuyến như: khe 
hở bánh răng, hệ số đàn hồi, mômen ma 
sát và mômen quán tính trên tải, hệ thống 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 24 35 
vẫn đảm bảo được độ chính xác trong cả 
chế độ động và chế độ tĩnh, sai số trong 
chế độ tĩnh luôn về 0 trong các trường 
hợp khác nhau. 
4. KẾT LUẬN 
Bài báo đã trình bày kết quả tổng hợp 
BĐK trượt LMI cho hệ cơ điện nhiều 
động cơ có liên hệ ma sát, đàn hồi. Phần 
trình bày được bắt đầu từ việc xây dựng 
mô hình cơ hệ, tìm luật điều khiển, chứng 
minh điều kiện ổn định, xây dựng mô 
hình mô phỏng, kiểm nghiệm bằng phần 
mềm Matlab-Simulink. Qua kiểm tra và 
so sánh với các kết quả của các công bố 
trước đây [3-7] cho thấy BĐK đã nâng 
cao được chất lượng của hệ thống truyền 
động nhiều động cơ thông qua các tiêu chí 
đánh giá, đó là: tính bền vững với nhiễu, 
đảm bảo khả năng quá tải về mômen, đảm 
bảo tốt đặc tính động và đặc tính tĩnh, 
đảm bảo tính chính xác bám. 
TÀI LIỆU THAM KHẢO 
[1] Dao Phuong Nam, Pham Tuan Thanh, Tran Xuan Tinh, Tran Thanh Dat, Pham Van Tu, “High gain 
observer based output feedback controller for a two-motor drive system: A separation principle 
approach”, Lecture Note in Electrical Engineering 465, Scopus Q3, Dec-2017. 
[2] Pham Tam Thanh, Dao Phuong Nam, Tran Xuan Tinh and Luong Cong Nho, “High-gain observer–
based sliding mode control of multimotor drive systems”, Book Adaptive robust control systems, 
Published by InTech Janeza Trdine 9, 51000 Rijeka, Croatia 2018. 
[3] B. Allaoua, A. Laoufi and B. Gasbaoui, “Multi-drive paper system control based on multi-input 
multi-output PID controller”, Leonardo Journal of Sciences, 2010. 
[4] Fawzan Salem, E.H.E. Bayoumi, “Robust fuzzy-PID control of three-motor drive system using 
simulated annealing optimization”, Journal of Electrical Engineering, 2011. 
[5] Li Jinmei, Liu Xingqiao, “Application of an Adaptive Controller with a Single Neuron in Control of 
Multi-motor Synchronous System”, IEEE, 2008. 
[6] A. Angermann, M. Aicher, and D. Schroder, “Time-optimal tension control forprocessing plants 
with continuous moving webs”, Proc. 35th Annual Meeting- IEEE Industry Applications Society, 
Rome, Oct. 1999. 
[7] H. Koc, D. Knittel, M.D. Mathelin, “Robust gain-scheduled control of winding systems”, IEEE Conf. 
Decision and Control, Sidney, Australia, Dec. 2000. 
[8] C. Scherer, S. Weiland, “Linear Matrix Inequalities in Control, Dutch Institute of Systems and 
Control (DISC)”, The Netherlands, 2005. 
[9] J. Zhang, “Solving Linear Matrix Inequality (LMI) Problems”, Advances in Industrial Control, 
Springer International Publishing Switzerland 2016, PP 203-224. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
36 Số 24 
Giới thiệu tác giả: 
Tác giả Trần Xuân Tình tốt nghiệp đại học chuyên ngành điện tử, nhận bằng Thạc 
sĩ chuyên ngành tự động hóa năm 2013. Tác giả hiện là giảng viên Bộ môn Kỹ 
thuật điện - Học viện Phòng không - Không quân. 
Lĩnh vực nghiên cứu: ứng dụng các giải pháp điều khiển hiện đại trong hệ 
truyền động điện. 
Tác giả Nguyễn Thị Linh nhận bằng tốt nghiệp đại học chuyên ngành kỹ sư điện – 
thiết bị điện, điện tử; bảo vệ luận án Thạc sĩ năm 2010 tại tại Trường Đại học 
Bách khoa Hà Nội. Tác giả hiện là giảng viên Khoa Kỹ thuật điện- Trường Đại học 
Điện lực. 
Lĩnh vực nghiên cứu: ứng dụng các giải pháp điều khiển hiện đại trong hệ 
thống điện. 
Tác giả Lê Văn Sâm tốt nghiệp đại học chuyên ngành điện tử, nhận bằng Thạc sĩ 
chuyên ngành tự động hóa, bằng Tiến sĩ chuyên ngành kỹ thuật điều khiển và tự 
động hóa năm 2019 tại Viện Kỹ thuật và Công nghệ quân sự. Tác giả hiện là giảng 
viên Bộ môn Kỹ thuật điện - Học viện Phòng không - Không quân. 
Lĩnh vực nghiên cứu: ứng dụng các giải pháp điều khiển hiện đại trong điều khiển 
thiết bị bay. 
Tác giả Phạm Đức Trung tốt nghiệp kỹ sư ngành hệ thống điện năm 2014; nhận 
bằng Thạc sỹ chuyên ngành kỹ thuật điện năm 2017 tại Trường Đại học Điện lực. 
Tác giả hiện đang là giảng viên Khoa Kỹ thuật điện, Trường Đại học Điện lực. 
Lĩnh vực nghiên cứu: nghiên cứu các giải pháp đo lường và điều khiển nhằm tối ưu 
các thiết bị điện trong vận hành hệ thống điện. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 24 37 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
38 Số 24