Xây dựng mô hình thủy động lực và vận chuyển bùn cát lơ lửng trên hệ tọa độ cong – Kiểm nghiệm mô hình với nghiệm của lời giải lý thuyết

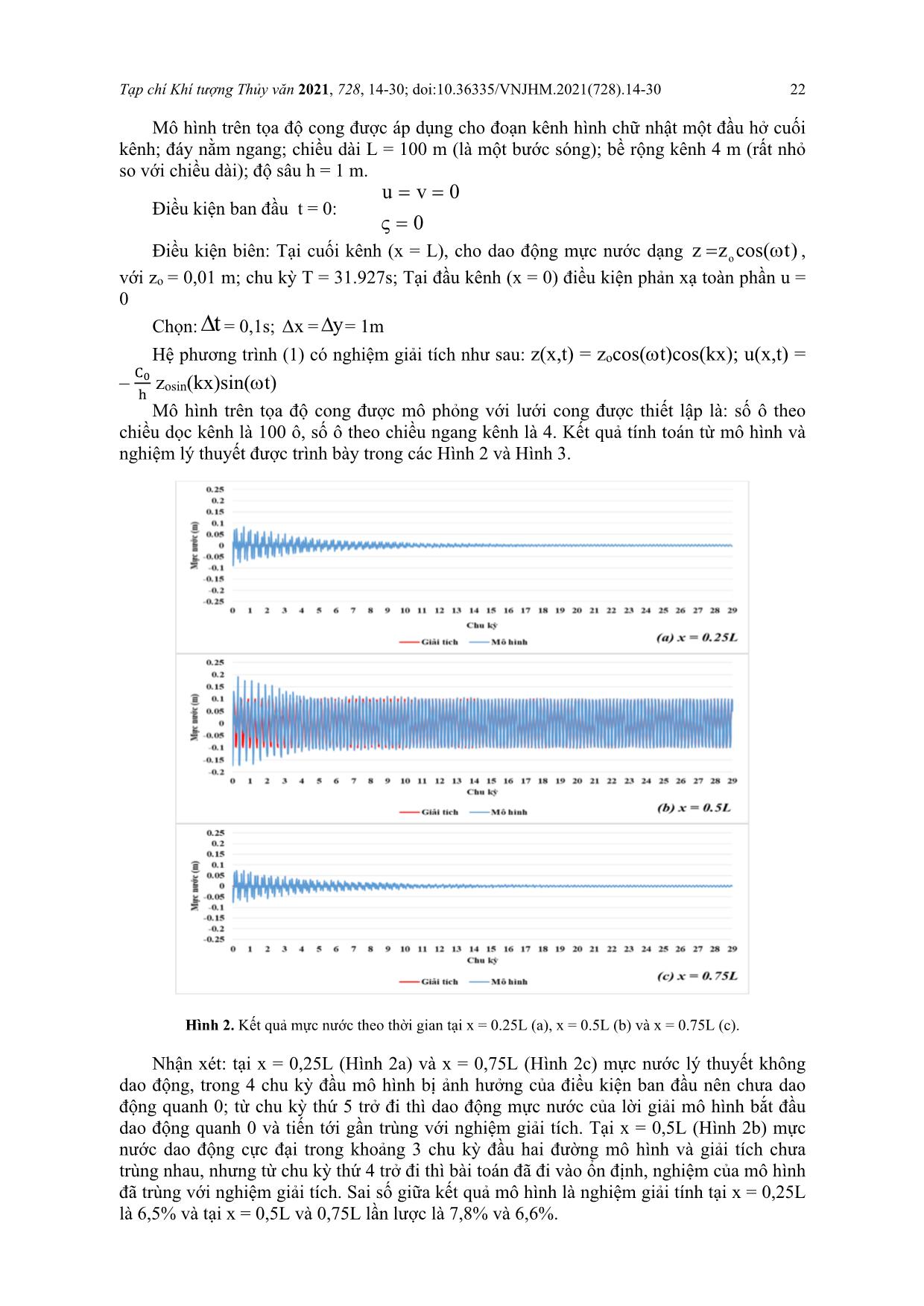
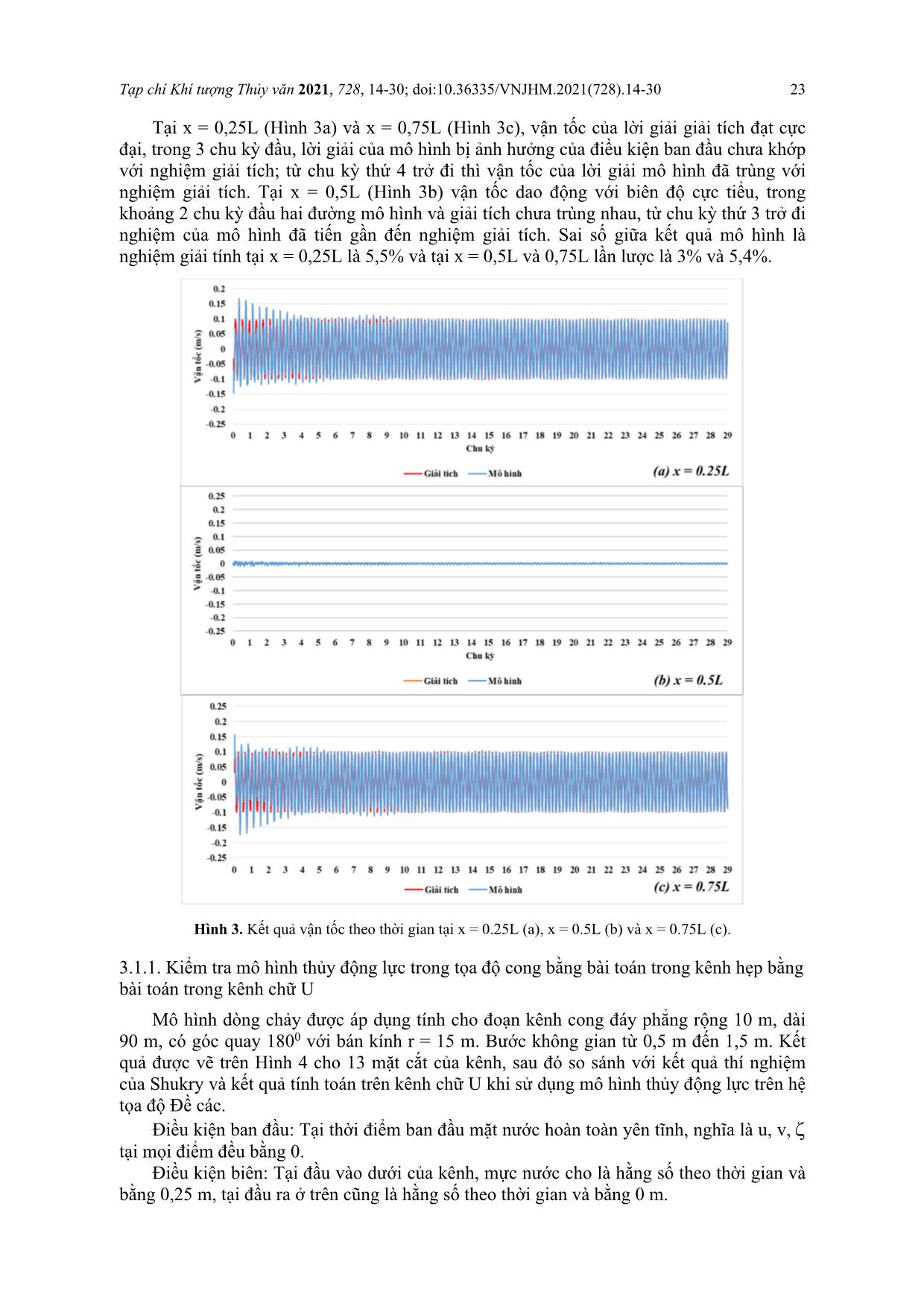
 Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30  
Bài báo khoa học 
Xây dựng mô hình thủy động lực và vận chuyển bùn cát lơ lửng 
trên hệ tọa độ cong – Kiểm nghiệm mô hình với nghiệm của lời 
giải lý thuyết 
Trần Thị Kim1,2,4, Nguyễn Khắc Thành Long3,4, Nguyễn Văn Phước5, Nguyễn Kỳ 
Phùng6, Nguyễn Thị Bảy3,4* 
1 Trường Đại học Tài nguyên và Môi trường Tp.HCM; ttkim@hcmunre.edu.vn 
2 Viện Môi trường và Tài nguyên, Đại học Quốc Gia Tp.HCM 
3 Trường Đại học Bách Khoa; ntbay@hcmut.edu.vn; nktl1107@gmail.com 
4 Đại học Quốc Gia Tp.HCM; ntbay@hcmut.edu.vn; nktl1107@gmail.com 
5 Liên hiệp các Hội Khoa học và Kỹ thuật Thành phố Hồ Chí Minh; 
nvphuoc196@gmail.com 
6 Viện Khoa học và Công nghệ tính toán; kyphungng@gmail.com 
*Tác giả liên hệ: ntbay@hcmut.edu.vn; Tel.: +84–902698585 
Ban Biên tập nhận bài: 12/4/2021; Ngày phản biện xong: 1/6/2021; Ngày đăng bài: 
25/8/2021 
Tóm tắt: Bài báo này trình bày về việc xây dựng mô hình toán thủy động lực và vận 
chuyển bùn cát lơ lửng dựa vào lời giải trên hệ tọa độ cong của hệ phương trình Reynolds, 
kết hợp với hệ phương trình chuyển tải bùn cát, lấy trung bình theo chiều sâu, có tính đến 
hàm số nguồn, mô tả tốc độ bốc lên hay lắng xuống của hạt. Độ tin cậy của hai mô hình 
này được kiểm định bằng kết quả của nghiệm giải tích. Kết quả cho thấy vào các chu kỳ 
đầu, dao động mực nước không ổn định, từ chu kỳ thứ năm trở đi, dao động mực nước và 
vận tốc giữa nghiệm giải tích và từ mô hình cho kết quả khá trùng khớp. Khi tính toán 
thủy lực trên kênh chữ U, kết quả tính toán trường vận tốc khi sử dụng mô hình thủy động 
lực trên tọa độ cong cho thấy ưu điểm hơn so với khi sử dụng mô hình thủy động lực trên 
hệ tọa độ đề các. Mô hình vận chuyển bùn cát lơ lửng được kiểm tra với kết quả từ nghiệm 
giải tích ứng với nhiều trường hợp khác nhau. Kết quả cho thấy không có sự sai biệt lớn 
giữa các giá trị nồng độ lan truyền trong không gian theo thời gian tính toán từ mô hình và 
nghiệm giải tích, cho thấy bước đầu độ tin cậy của mô hình vừa được thiết lập là chấp 
nhận được. 
Từ khóa: Thủy động lực; Vận chuyển bùn cát lơ lửng; Hệ tọa độ cong. 
1. Mở đầu 
Bùn cát trong sông gồm các hạt khoáng chất, cát, sỏi, cuội, đá dăm, đá tảng chuyển 
động trong dòng nước hay lắng đọng trong lòng sông. Chúng được hình thành một phần do 
quá trình phong hóa, bào mòn và xâm thực trên bề mặt lưu vực và sau đó bị gió và nước 
cuốn trôi vào lòng sông; một phần do quá trình xói lở chính bản thân trong lòng sông như 
sụt lở bờ, xói mòn đáy [1]. 
Với sự phát triển nhanh chóng của các phương pháp, mô hình tính toán đã trở thành 
một công cụ hữu ích để nghiên cứu chế độ thủy động lực học của dòng chảy và quá trình 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 15 
vận chuyển bùn cát trong sông, hồ và các vùng ven biển [2]. Rất nhiều mô hình thương mại 
với giá thành cao đã ra đời với những ứng dụng linh hoạt đã được nhiều nhà khoa học sử 
dụng để mô phỏng vận chuyển bùn cát, điển hình như bộ mô hình MIKE21 và MIKE3 của 
DHI, được phát triển bởi Viện Thủy Lực Đan Mạch. Mô hình được xây dựng tích hợp rất 
nhiều công cụ mạnh, có thể giải quyết các bài toán cơ bản trong lĩnh vực tài nguyên nước 
[3]. Ngoài ra, có rất nhiều mô hình được thiết lập bởi các nhà khoa học như: Mô hình 
TELEMAC được bắt đầu phát triển từ năm 1987 do Tập đoàn Điện lực Pháp (EDF) chủ trì 
[4]; Mô hình SHORECIRC được phát triển năm 1999 [5]; Mô hình thủy lực CCHE2D do 
Jin và Wang phát triển năm 1999 [6]; Mô hình SUTRENCH–2D: Mô hình thủy động lực và 
vận chuyển bùn cát do Van Rijn và Tan phát triển năm 1985 và được hoàn thiện tính toán 
bùn cát kết dính vùng cửa sông đến năm 2007 [7]; Mô hình TABS–2: được phát triển năm 
1985 [8]. 
Ở nước ta, cũng có rất nhiều mô hình tính toán dòng chảy và vận chuyển bùn cát trong 
sông, các mô hình này là mã nguồn mở, thuận lợi cho việc chỉnh sửa code cũng như kết nối 
với các hệ thống khác. Điển hình có các mô hình như: Mô hình Delta; Mô hình SAL và 
VRSAP–SAL: Do Nguyễn Tất Đắc phát triển từ năm 1980 và sau đó được nâng cấp và kết 
hợp với mô hình VRSAP để tạo thành mô hình mang tên VRSAP–SAL hoàn thiện hơn về 
thuật toán và chương trình [9]; Mô hình KOD–01 và KOD–02 [10–11]; Mô hình MK4 [12]. 
Mô hình TREM là mô hình biến dạng lòng dẫn 2 chiều trong hệ tọa độ phi tuyến không 
trực giao cho phép xác định sự phân bố tốc độ cũng như biến đổi đáy sông theo cả hướng 
dọc và hướng ngang. Mô hình này đã áp dụng và cho kết quả tốt cho nhiều đoạn sông cong 
trên sông Hồng [13–15]. 
Các kết quả nghiên cứu ứng dụng mô hình này trên thế giới cũng như ở trong nước, 
cho thấy mô hình vẫn dự báo tốt diễn biến lòng dẫn, mà chủ yếu là diễn biến đáy qua việc 
giải các phương trình liên quan đến thủy lực và vận chuyển bùn cát. Tuy nhiên, tại đường 
bờ của các khu vực nghiên cứu, kết quả từ các mô hình toán trên hệ tọa độ Đề các vẫn còn 
bị sai số, đặc biệt là tại các vùng nghiên cứu ... ợng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 23 
Tại x = 0,25L (Hình 3a) và x = 0,75L (Hình 3c), vận tốc của lời giải giải tích đạt cực 
đại, trong 3 chu kỳ đầu, lời giải của mô hình bị ảnh hưởng của điều kiện ban đầu chưa khớp 
với nghiệm giải tích; từ chu kỳ thứ 4 trở đi thì vận tốc của lời giải mô hình đã trùng với 
nghiệm giải tích. Tại x = 0,5L (Hình 3b) vận tốc dao động với biên độ cực tiểu, trong 
khoảng 2 chu kỳ đầu hai đường mô hình và giải tích chưa trùng nhau, từ chu kỳ thứ 3 trở đi 
nghiệm của mô hình đã tiến gần đến nghiệm giải tích. Sai số giữa kết quả mô hình là 
nghiệm giải tính tại x = 0,25L là 5,5% và tại x = 0,5L và 0,75L lần lược là 3% và 5,4%. 
Hình 3. Kết quả vận tốc theo thời gian tại x = 0.25L (a), x = 0.5L (b) và x = 0.75L (c). 
3.1.1. Kiểm tra mô hình thủy động lực trong tọa độ cong bằng bài toán trong kênh hẹp bằng 
bài toán trong kênh chữ U 
Mô hình dòng chảy được áp dụng tính cho đoạn kênh cong đáy phẳng rộng 10 m, dài 
90 m, có góc quay 1800 với bán kính r = 15 m. Bước không gian từ 0,5 m đến 1,5 m. Kết 
quả được vẽ trên Hình 4 cho 13 mặt cắt của kênh, sau đó so sánh với kết quả thí nghiệm 
của Shukry và kết quả tính toán trên kênh chữ U khi sử dụng mô hình thủy động lực trên hệ 
tọa độ Đề các. 
Điều kiện ban đầu: Tại thời điểm ban đầu mặt nước hoàn toàn yên tĩnh, nghĩa là u, v,  
tại mọi điểm đều bằng 0. 
Điều kiện biên: Tại đầu vào dưới của kênh, mực nước cho là hằng số theo thời gian và 
bằng 0,25 m, tại đầu ra ở trên cũng là hằng số theo thời gian và bằng 0 m. 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 24 
Hình 4. Kết quả tính toán cho kênh chữ U bằng mô hình thủy động lực trên tọa độ cong (a), thí 
nghiệm của Shukry [23] (b) và kết quả tính toán trên kênh chữ U khi sử dụng mô hình thủy động 
lực trên hệ tọa độ Đề các (c). 
Kết quả cho thấy trường vận tốc khi tính bằng mô hình thủy động lực trên tọa độ cong 
(Hình 4a) khá phù hợp với kết quả từ thí nghiệm của Shukry (Hình 4b). Sau khu vực uốn 
cong, trường vận tốc bị ép về phía bên bờ lõm (Hình 4a) và đây cũng là nguyên nhân chính 
gây nên hiện tượng xói lở khu vực này trong các đoạn cong của sông thiên nhiên. Khi tính 
toán bằng mô hình thủy động lực trên hệ tọa độ Đề các (Hình 4c), kết quả vận tốc sát bờ 
không tối ưu bằng tính trên hệ tọa độ cong, khi sau khu vực uống cong, vận tốc bên bờ lõm 
lại nhỏ, gần như tiến về 0. 
3.2. Kiểm tra mô hình vận chuyển bùn cát lơ lửng 
Mô hình vận chuyển bùn cát lơ lửng được kiểm định với trường hợp miền tính đồng 
nhất, có chiều sâu không đổi, vận tốc u, v là hằng số, hệ số khuyếch tán rối theo phương 
ngang K là hằng số, có một nguồn tức thời đổ vào miền tính với khối lượng M, hệ 
phương trình (14) có nghiệm giải tích như sau [24–25]: 
2 2
0 0
x yx y
(x x ut) (y y vt)M / H D
c(x, y, t) exp t
4K t 4K t H4 K K t
 (33) 
Trong đó M là khối lượng phẩm màu được đổ vào điểm tọa độ (x0, y0) trong miền tính 
bắt đầu tại thời điểm t > 0, miền tính có ma sát bằng 0. 
Tính toán được thực hiện cho miền tính vuông có độ sâu không đổi bằng 5m, kích 
thước 5000m x 5000m, với x = y = 50 m, vận tốc lắng đọng D = 0,00002 m/s, T = 10s, 
nguồn đổ vào miền tính tại vị trí (x0 = 30 x; y0 = 30 y) có khối lượng M. 
3.2.1. Trường hợp 1: Khối lượng phẩm màu được đổ vào điểm tọa độ (x0, y0) là M = 2500 
kg 
Mô hình được áp dụng tính trong 5,5 giờ với hệ số khuếch tán như sau: 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 25 
(i) TH1A: K = 4m
2/s; u = v = 0,1m/s. 
(ii) TH1B: K = 4m
2/s; u = 0,1m/s; v = 0m/s. 
(iii) TH1C: K = 4m
2/s; u = 0m/s; v = 0,1m/s. 
Các kết quả tính được trình bày dưới dạng các đường đồng mức nồng độ lần lượt tại 6 
điểm thời gian (t = 0,5 giờ; 1,5 giờ; 2,5 giờ; 3,5 giờ; 4,5 giờ; 5,5 giờ) từ nghiệm giải tích 
(Hình 5a, 6a và 7a) và từ mô hình (Hình 5b, 6b và 7b). Nồng độ tại vị trí (x0 = 30 x; y0 = 
30 y) là C = 0,2 kg/m3 (C = 


, với M là khối lượng và V là thể tích của ô). 
Hình 5. Kết quả tính toán cho TH1A bằng nghiệm giải tích (a) và bằng mô hình (b). 
Hình 6. Kết quả tính toán cho TH1B bằng nghiệm giải tích (a) và bằng mô hình (b). 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 26 
Hình 7. Kết quả tính toán cho TH1C bằng nghiệm giải tích (a) và bằng mô hình (b). 
Kết quả cho thấy không có sự sai biệt lớn giữa kết quả tính toán trong 3 trường hợp khi 
sử dụng bằng mô hình và nghiệm giải tích. 
Trong trường hợp 1A: Khi vận tốc theo phương u và v bằng nhau (bằng 0,1), nguồn 
thải lan truyền với hệ số khuếch tán K = 4 m
2/s theo hướng 45 độ cho cả kết quả từ mô 
hình 5a và nghiệm giải tích hình 5b. 
Trong trường hợp 1B: Khi vận tốc theo phương thẳng đứng v = 0 m/s, nguồn đổ vào 
miền tính tại vị trí (x0 = 30 x; y0 = 30 y) lan truyền thẳng theo phương ngang cho cả kết 
quả từ mô hình 6a và nghiệm giải tích hình 6b. 
Trong trường hợp 1C: Khi vận tốc theo phương ngang u = 0 m/s, nguồn đổ vào miền 
tính lan truyền thẳng theo phương thẳng đứng cho cả kết quả từ mô hình 7a và nghiệm giải 
tích hình 7b. 
Khi tính tiếp tục đến 8,5 giờ ứng với TH1A (Hình 8), kết quả tính toán khi sử dụng 
bằng mô hình và nghiệm giải tích cho thấy: khi nồng độ lan truyền đến vị trí biên, do ảnh 
hưởng bởi điều kiện biên, nồng độ sẽ đọng lại tại vùng biên (Hình 8b). 
Hình 8. Kết quả tính toán tiếp tục đến 8,5 giờ cho TH1A bằng nghiệm giải tích (a) và bằng mô 
hình (b). 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 27 
3.2.2. Trường hợp 2: Khối lượng phẩm màu được đổ vào điểm tọa độ (x0, y0) là M = 1000 
kg, tính trong 10 giờ và mở rộng vùng tính lên kích thước 6000m x 6000m 
Để thấy rõ sự lắng đọng hoàn toàn của khối lượng phẩm màu đổ vào điểm tọa độ (x0, 
y0), tính toán sẽ thực hiện với khối lượng phẩm màu giảm xuống còn M = 1000 kg, tính 
trong 10 giờ và mở rộng vùng tính lên kích thước 6000m x 6000m. Vậy nồng độ tại điểm 
tọa độ (x0, y0) là 0,08 kg/m3. Kết quả tính toán sau 9,5 giờ cho thấy, nồng độ C = 0,0001 
kg/m3 sẽ lắng đọng hoàn toàn. Kết quả tính toán bằng mô hình (Hình 9b) phù hợp với kết 
quả tính từ nghiệm giải tích (Hình 9a). 
Hình 9. Kết quả tính toán khi giảm khối lượng bùn và mở rộng vùng tính bằng nghiệm giải tích (a) 
và bằng mô hình (b). 
Nhìn chung, kết quả từ mô hình khá phù hợp với kết quả từ nghiệm giải tích. Nghiên 
cứu này bước đầu cho thấy sự tin cậy của mô hình chuyển tải trong hệ tọa độ vừa được thiết 
lập. 
4. Kết luận 
Xây dựng mô hình thủy động lực và vận chuyển bùn cát lơ lửng trên hệ tọa độ cong 
với: (1) Mô hình thủy động lực trong tọa độ cong được xây dựng dựa trên hệ phương trình 
Reynolds trung bình theo chiều sâu. Lưới tính toán được xây dựng nhờ giải phương trình 
Ellip dưới dạng đạo hàm riêng phần. Các phương trình chuyển động, sau khi chuyển sang 
tọa độ cong, sẽ được giải trên lưới này; (2) Mô hình vận chuyển bùn cát lơ lửng trong tọa 
độ cong, được tính xen kẽ với mô hình thủy động lực thì dựa trên hệ phương trình chuyển 
tải bùn cát 2D trên hệ tọa độ Đề các. Hai mô hình này được kiểm định bằng nghiệm của lời 
giải lý thuyết. 
Kết quả cho thấy, khi tính toán mực nước và vận tốc, thì các chu kỳ đầu dao động 
không ổn định, từ chu kỳ thứ năm trở đi, diễn biến mực nước và vận tốc giữa nghiệm giải 
tích và từ mô hình cho kết quả khá trùng khớp nhau. Khi tính toán thủy lực trên kênh chữ 
U, kết quả tính toán trường vận tốc khi sử dụng mô hình thủy động lực trên tọa độ cong cho 
thấy ưu điểm hơn so với khi sử dụng mô hình thủy động lực trên hệ tọa độ đề các. Mô hình 
vận chuyển bùn cát lơ lửng được kiểm tra với nhiều trường hợp (có cả vận tốc theo phương 
thẳng đứng và phương ngang, có vận tốc theo phương đứng và trường hợp cuối là chỉ có 
vận tốc theo phương ngang). Các kết quả thu được từ mô hình phù hợp với kết quả tính từ 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 28 
nghiệm giải tích, điều này khẳng định độ tin cậy của mô hình vừa được thiết lập, có thể áp 
dụng tính toán cho một vùng nghiên cứu vụ thể. Tuy nhiên, mô hình này vẫn chưa xây 
dựng giao diện cho người sử dụng. 
Đóng góp của tác giả: Xây dựng ý tưởng nghiên cứu: K.T.T.; P.N.K.; P.N.V.; L.N.K.T.; 
Lựa chọn phương pháp nghiên cứu: K.T.T.; P.N.K; P.N.V.; Xử lý số liệu: L.N.K.T.; Mô 
hình hóa: K.T.T.; Lập trình: K.T.T.; L.N.K.T.; Phân tích kết quả: K.T.T.; B.N.T.; L.N.K.T.; 
Chỉnh sửa bài báo: K.T.T.; B.N.T. 
Lời cảm ơn: NCS Trần Thị Kim, Mã số: 2020.TS.102 được tài trợ bởi Tập đoàn Vingroup 
– Công ty CP và hỗ trợ bởi Chương trình học bổng đào tạo thạc sĩ, tiến sĩ trong nước của 
Quỹ Đổi mới sáng tạo Vingroup (VINIF), Viện Nghiên cứu Dữ liệu lớn (VINBIGDATA). 
Lời cam đoan: Tập thể tác giả cam đoan bài báo này là công trình nghiên cứu của tập thể 
tác giả, chưa được công bố ở đâu, không được sao chép từ những nghiên cứu trước đây; 
không có sự tranh chấp lợi ích trong nhóm tác giả. 
Tài liệu tham khảo 
1. Van, R. L.C. Sediment transport, part I: bed load transport. J. Hydraul. Eng. 1984, 
110, 1431–1456. 
2. Rinaldi, M.; Wyzga, B.; Dufour, S.; Bertoldi, W.; Gurnell, A. River Processes and 
Implications for Fluvial Ecogeomorphology: A European Perspective. In: John F. 
Shroder (ed.) Treatise on Geomorphology, San Diego: Academic Press, 2013, 12, 
37–52. 
3. DHI, MIKE 21 & MIKE 3 Flow Model FM. Hydrodynamic and Transport Module, 
2012. 
4. Galland, J.C.; Goutal, N.; Hervouet, J.M. TELEMAC: A new numerical model for 
solving shallow water equations. J. Adv. Water Resour. 1991, 14, 138–148. 
5. Putrevu, U.; Svendsen, I.A. Three–dimensional dispersion of momentum in wave–
induced nearshore currents. Eur. J. Mech. B Fluids. 1999, 18, 409–427. 
6. Jia, Y.; Wang S.S. Numerical model for channel flow and morphological change 
studies. J. Hydraul. Eng. 1999, 125, 924–933. 
7. Van, R. L.C. Unified view of sediment transport by currents and waves. I: Initiation 
of motion, bed roughness, and bed–load transport. J. Hydraul. Eng. 2007, 133, 
649–667. 
8. Thomas, W.A.; McAnally, W.H. User's Manual for the Generalized Computer 
Program System Open–Channel Flow and Sedimentation TABS–2. Main Text and 
Appendices A through O, 1985. 
9. Đắc, N.T. Mô hình toán cho dòng chảy và chất lượng nước trên hệ thống kênh 
sông. NXB Nông nghiệp, 2005, 234. 
10. Nien, N.A. Possible use of flood water for reclamation of acid sulphate soils in the 
Plain of Reeds (Mekong Delta). Workshop on Management of Acid Sulphate Soils, 
Ho Chi Minh City, 1995. 
11. Nien, N.A.; Duong N.B. The Third Invariant Form of Hydrodynamic Equations and 
Application for Definition of Water Hammer Characteristics in Pipe. Automation 
2014, pp. 85. 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 29 
12. Giang, L.S. MK4–A software for hydraulic and substances transport computation 
in river. In symposium fluid mechanic and natural disaster prevent. 1999, 124–134. 
13. Khai, N.H.; Giang, N.T.; Anh N.T. Research using 2–D model to evaluate 
the changes of riverbed. VNU J. Sci. 2003, 19, 47. 
14. Khải, N.H.; Giang, N.T. Nghiên cứu ứng dụng mô hình 2 chiều tính toán biến dạng 
lòng dẫn. Tạp chí Khí tượng Thủy văn 2003, 512, 8–15. 
15. Giang, N.T.; Đại, H.V. Đánh giá ảnh hưởng của các phương án chỉnh trị đến khả bồi 
xói của đoạn sông Hồng từ Cầu Long Biên đến Khuyến Lương bằng mô hình mô 
phỏng biến đổi lòng dẫn hai chiều. Tạp chí Khoa học ĐHQGHN 2011, 27, 44–53. 
16. Bay, N.T.; Toan, T.T.; Phung, N.K.; Nguyen–Quang, T. Numerical investigation 
on the sediment transport trend of Can Gio Coastal Area (Southern Vietnam). J. 
Mar. Environ. Eng. 2012, 9, 191. 
17. Massel, S.R., Hydrodynamics of coastal zones. Elsevier,1989. 
18. Thompson, J.F.; Warsi Z.U.; Mastin C.W. Numerical grid generation: foundations 
and applications. 1985. 
19. Fletcher, C. Computational Techniques for Fluid Dynamics [Russian translation], 
Mir. Moscow. 1991. 
20. Fletcher, C.A. Computational techniques for fluid dynamics 2: Specific techniques 
for different flow categories, Springer–Verlag 2012. 
21. Van Rijn, L.C. Mathematical modeling of suspended sediment in nonuniform 
flows. J. Hydraul. Eng. 1986, 112, 433–455. 
22. Van Rijn, L.C. Sedimentation of dredged channels by currents and waves. J. 
Waterw. Port Coast. Ocean Eng. 1986, 112, 541–559. 
23. Shukry, A. Flow around bends in an open flume. Transactions ASCE. 1950, 115, 
751–78. 
24. Ippen, A.T. Estuary and coastline hydrodynamics. McGraw–Hill Book Company, 
1966. 
25. Bảy, N.T.; Trang, M.Q. Mô hình tính tóan chuyển tải bùn cát kết dính vùng ven 
biển– Phần I: Mô hình tính tóan. Tạp chí Phát triển Khoa học và Công nghệ 
ĐHQG Tp HCM 2006, 9, 53–60. 
A coupled hydraulic and sediment transport model in the 
curvilinear coordinate 
Tran Thi Kim1,2,4, Nguyen Khac Thanh Long3,4, Nguyen Van Phuoc5, Nguyen Ky 
Phung6, Nguyen Thi Bay3,4* 
1 Ho Chi Minh City University of Natural Resources and Environment; 
ttkim@hcmunre.edu.vn 
2 Institute of Environment and Natural Resources, Vietnam National University Ho Chi 
Minh City; ttkim@hcmunre.edu.vn 
3 University of Technology; ntbay@hcmut.edu.vn 
4 Vietnam National University Ho Chi Minh City; ntbay@hcmut.edu.vn 
5 Ho Chi Minh City Union of Science and Technology associations; 
nvphuoc196@gmail.com 
6 Institute of Computational Science and Technology; kyphungng@gmail.com 
Tạp chí Khí tượng Thủy văn 2021, 728, 14-30; doi:10.36335/VNJHM.2021(728).14-30 30 
Abstract: This paper focuses on constructing a couple hydraulic and suspended sediment 
transport model on the curvilinear coordinate system. The original equations are the 
Reynolds equation system couple with the equations for suspended sediment transport, 
which averaged over the depth and combined a source function, describes the velocity of 
particles rising or settling. The reliability of these two models is verified by analytic 
solutions. The results show that, in the first periods, the water level fluctuation is unstable. 
From the fifth period onwards, the fluctuation of water level and velocity between 
analytical solution and model results show a good agreement. The suspended sediment 
transport model was verified in some cases (with both vertical and horizontal velocities, 
vertical velocities only, and horizontal velocities only). The verification results of the 
suspended sediment transport model do not have great differences between the simulation 
results in some cases when using the model and analytical solution. The results obtained 
that the model results are consistent with the analytical solution results, which mean that it 
initially confirms the reliability of the model. This study aims to build open source models 
for convenience of the connection with other models as well as prediction systems. 
Keywords: Hydraulic; Suspended sediment transport; The curvilinear coordinate systems.