Về một phương pháp xác định tư thế ban đầu cho hệ dẫn đường quán tính không đế ở chế độ la bàn trên đối tượng xe cơ giới

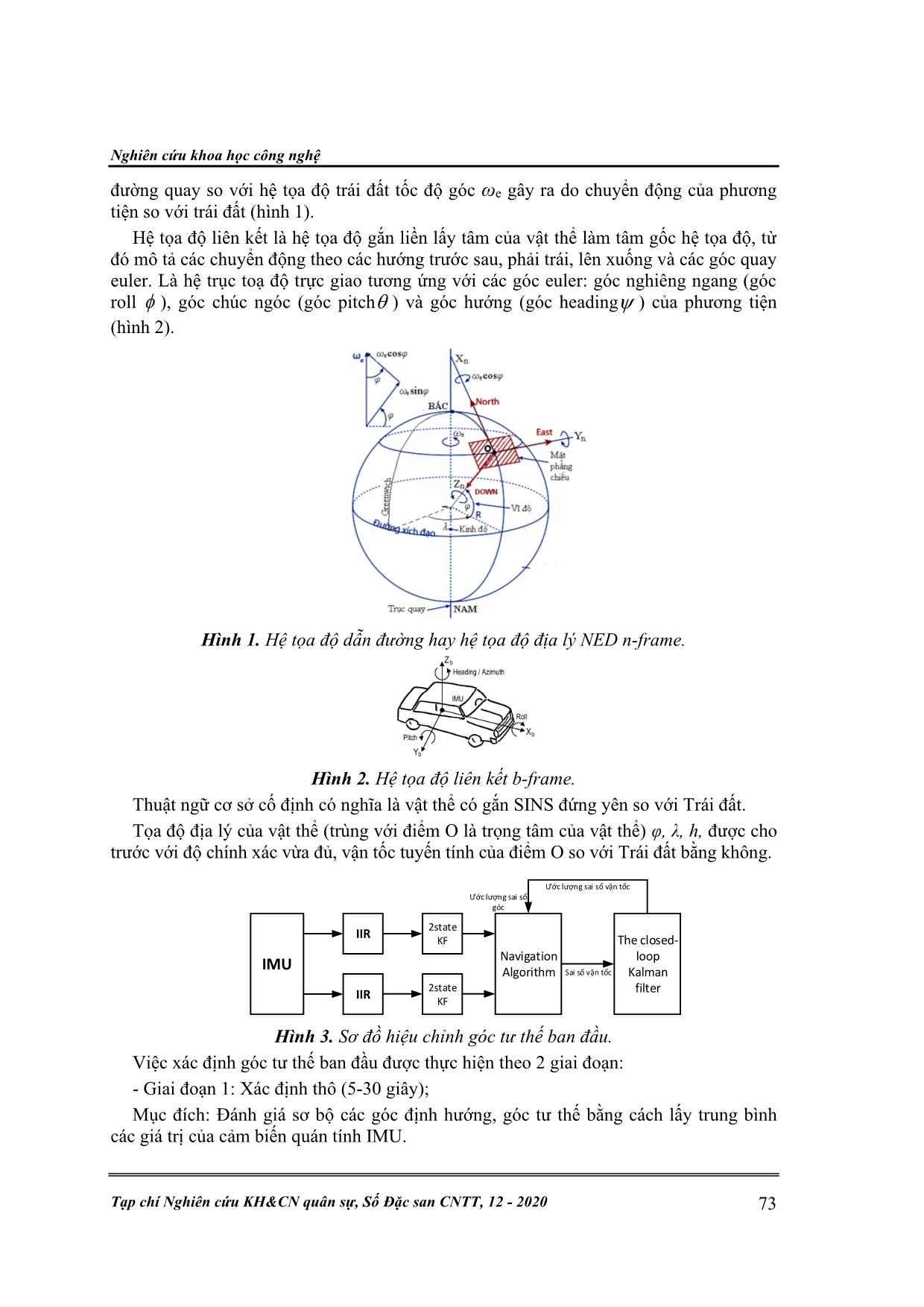
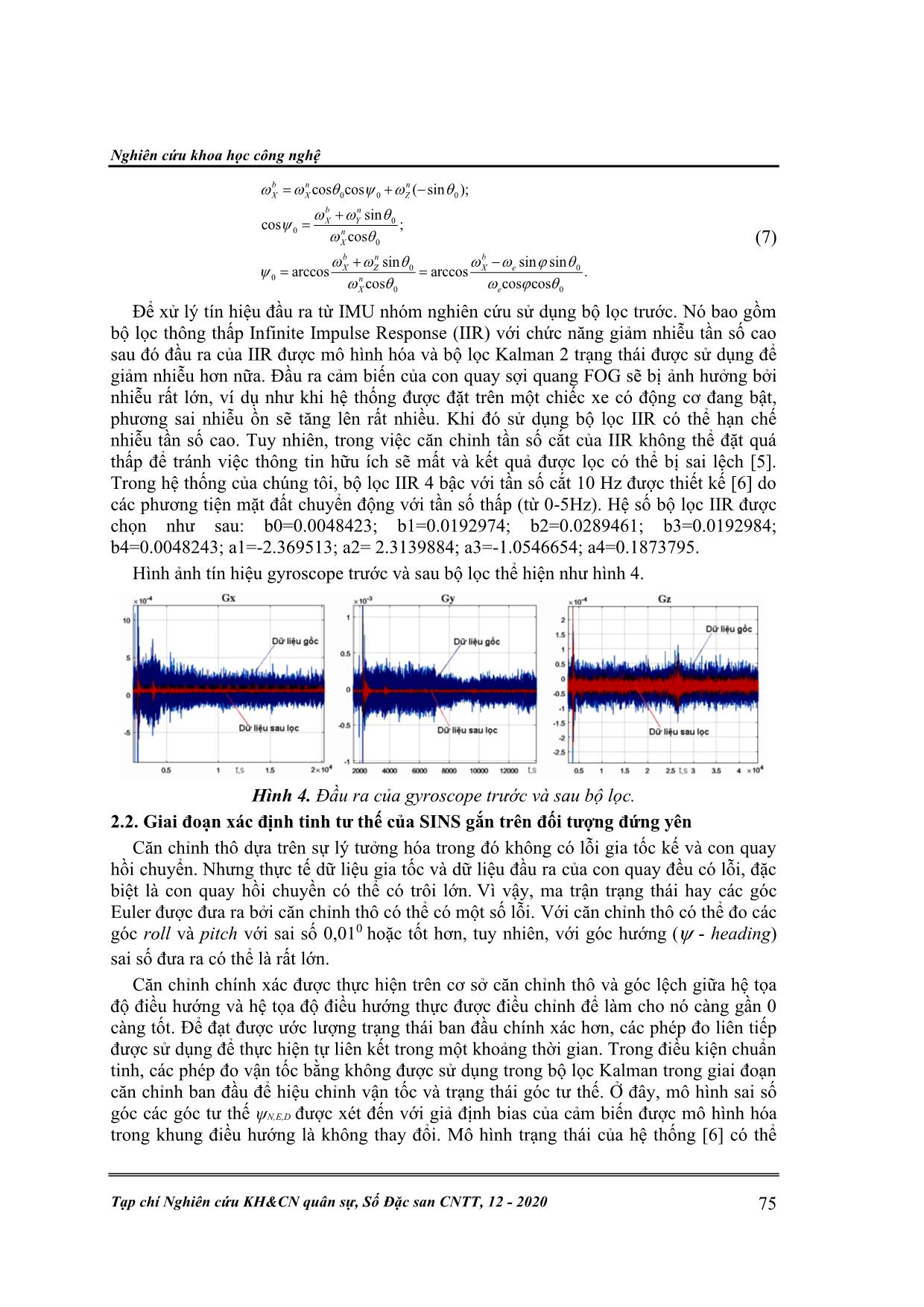
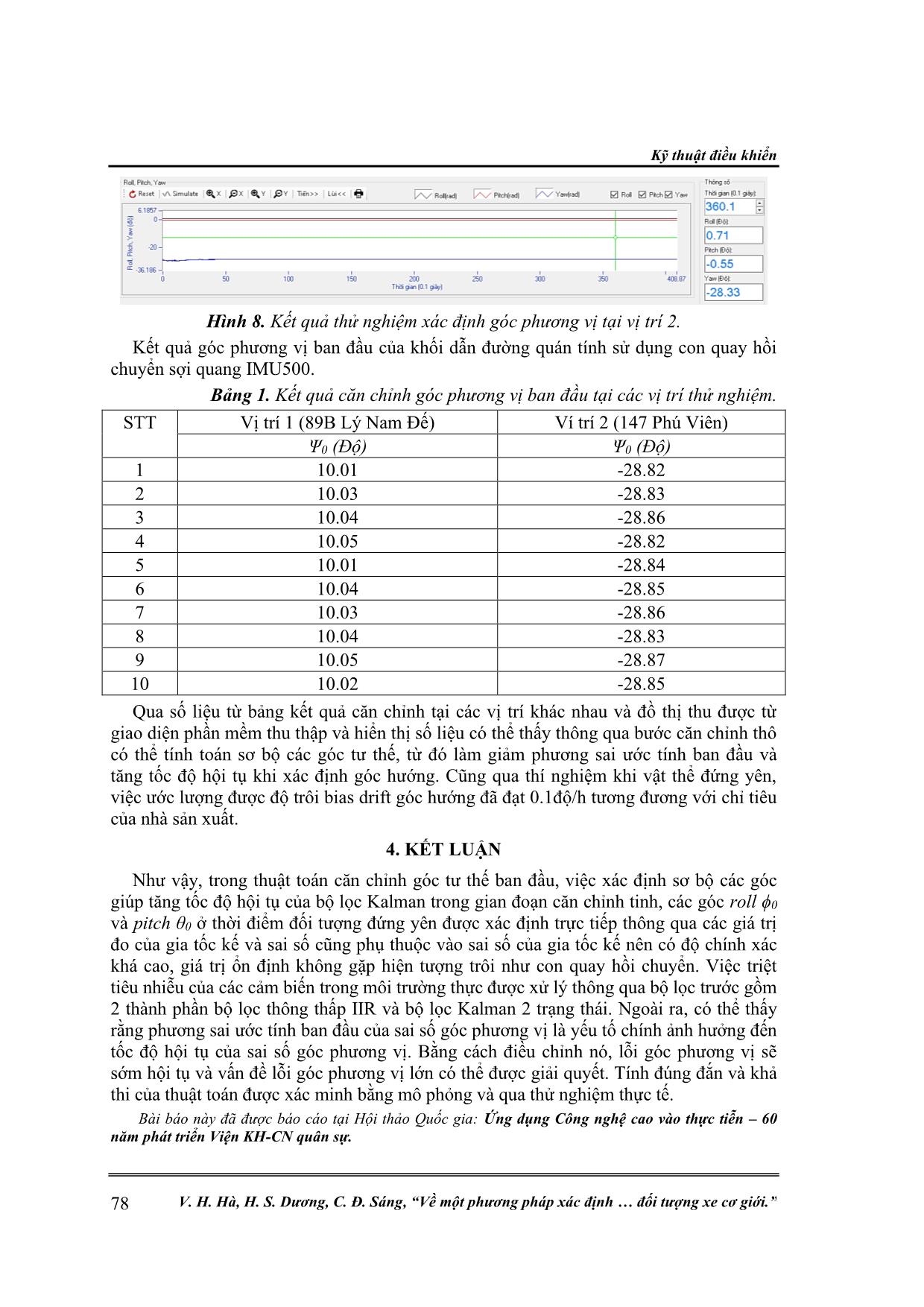
Kỹ thuật điều khiển 
 72 V. H. Hà, H. S. Dương, C. Đ. Sáng, “Về một phương pháp xác định  đối tượng xe cơ giới.” 
VỀ MỘT PHƯƠNG PHÁP XÁC ĐỊNH TƯ THẾ BAN ĐẦU 
CHO HỆ DẪN ĐƯỜNG QUÁN TÍNH KHÔNG ĐẾ Ở CHẾ ĐỘ LA BÀN 
TRÊN ĐỐI TƯỢNG XE CƠ GIỚI 
Vũ Hải Hà*, Hồ Sỹ Dương, Cao Đức Sáng 
Tóm tắt: Đối với hệ thống dẫn đường quán tính, việc xác định chính xác góc tư thế ban 
đầu có vai trò vô cùng quan trong, ảnh hưởng trực tiếp đến quá trình điều hướng sau này 
của hệ thống. Bài báo đề cập tới thuật toán xác định tư thế ban đầu bao gồm hướng bắc 
thực cho hệ thống dẫn đường quán tính không đế SINS trên vật thể không chuyển động ở 
chế độ la bàn con quay gyrocompass. Thuật toán được thực hiện theo hai giai đoạn là xác 
định tư thế ban đầu sơ bộ và xác định tư thế ban đầu chính xác dựa trên các vectơ trạng 
thái của khối đo lường quán tính IMU. Kết quả nhận được đã chứng minh tính chính xác 
của thuật toán. 
Từ khóa: Alignment; SINS; IMU; Góc định hướng; La bàn. 
1. ĐẶT VẤN ĐỀ 
Theo nghĩa rộng, có thể hiểu việc xác định tư thế của hệ thống dẫn đường quán tính 
có thể chia thành xác định tư thế ban đầu và xác định tư thế khi vận động. Xác định, hiệu 
chỉnh góc tư thế ban đầu (initial alignment) của hệ thống dẫn đường quán tính không đế 
(SINS) là một quá trình quan trọng được thực hiện trước khi đến bước điều hướng thông 
thường [1], như ta đã biết rằng kết quả xác định, hiệu chỉnh góc ban đầu của hệ thống có 
tầm quan trọng cơ bản ảnh hưởng trực tiếp đến độ chính xác của quá trình điều hướng 
cho hệ thống dẫn đường quán tính. 
Để bắt đầu các thuật toán trong hệ thống dẫn đường quán tính (SINS), trước tiên cần 
nhập các điều kiện ban đầu: tọa độ, tốc độ và các tham số hướng đối tượng. Bản chất của 
việc đưa ra các tham số góc ban đầu là xác định vị trí góc của vật thể so với hệ tọa độ địa 
lý. Có hai loại phương pháp đưa ra góc ban đầu đó là: xác định góc ban đầu ở chế độ tự 
trị của SINS và xác định góc ban đầu được lấy từ các nguồn thông tin bên ngoài (ví dụ 
như: la bàn, máy đo từ trường, hệ thống định vị vệ tinh). 
Trong chế độ tự trị việc xác định góc ban đầu lấy thông tin đo đầu vào là gia tốc trọng 
trường của Trái đất, tốc độ góc của Trái đất và tọa độ vật thể từ đó đưa ra giá trị các góc 
so với hệ tọa độ địa lý OXgYgZg. Vị trí này được mô tả bởi các góc heading ψ0, pitch θ0, 
roll ϕ0, là các góc cần tìm của bài toán xác định tư thế ban đầu [2]. Về mặt lý thuyết, các 
phương pháp phân tích, xác định tư thế ban đầu của hệ thống dẫn đường quán tính không 
đế ở chế độ tự trị có chức năng tương đương với các la bàn con quay vật lý trên các hệ 
gắn chặt. 
 2. XÁC ĐỊNH GÓC BAN ĐẦU VỚI SINS GẮN TRÊN VẬT THỂ ĐỨNG YÊN 
Mục tiêu xác định tư thế ban đầu của SINS trên cơ sở cố định là xác định hướng ban 
đầu của hệ tọa độ liên kết so với hệ tọa độ dẫn đường bằng cách đọc các cảm biến quán 
tính (gia tốc kế accelerometer, cảm biến vận tốc góc gyroscopes). 
Hệ tọa độ dẫn đường (n-frame) OXnYnZn là hệ tọa độ đo đạc cục bộ với tâm của nó 
trùng khớp với hệ toạ độ của cảm biến quán tính, trục X chỉ về hướng Bắc, trục Y chỉ về 
hướng Đông, trục Z vuông góc trực giao với mặt phẳng chiếu được hướng xuống dưới 
(NED) hoặc lên trên (NEU), và trục z xác định theo quy tắc bàn tay phải. Hệ tọa độ dẫn 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 73 
đường quay so với hệ tọa độ trái đất tốc độ góc ωe gây ra do chuyển động của phương 
tiện so với trái đất (hình 1). 
Hệ tọa độ liên kết là hệ tọa độ gắn liền lấy tâm của vật thể làm tâm gốc hệ tọa độ, từ 
đó mô tả các chuyển động theo các hướng trước sau, phải trái, lên xuống và các góc quay 
euler. Là hệ trục toạ độ trực giao tương ứng với các góc euler: góc nghiêng ngang (góc 
roll  ), góc chúc ngóc (góc pitch ) và góc hướng (góc heading ) của phương tiện 
(hình 2). 
Hình 1. Hệ tọa độ dẫn đường hay hệ tọa độ địa lý NED n-frame. 
Hình 2. Hệ tọa độ liên kết b-frame. 
Thuật ngữ cơ sở cố định có nghĩa là vật thể có gắn SINS đứng yên so với Trái đất. 
Tọa độ địa lý của vật thể (trùng với điểm O là trọng tâm của vật thể) φ, λ, h, được cho 
trước với độ chính xác vừa đủ, vận tốc tuyến tính của điểm O so với Trái đất bằng không. 
IIR
IIR
IMU
Navigation 
Algorithm
The closed-
loop 
Kalman 
filter
Sai số vận tốc
Ước lượng sai số vận tốc
Ước lượng sai số 
góc
2state
KF
2state
KF
Hình 3. Sơ đồ hiệu chỉnh góc tư thế ban đầu. 
Việc xác định góc tư thế ban đầu được thực hiện theo 2 giai đoạn: 
- Giai đoạn 1: Xác định thô (5-30 giây); 
Mục đích: Đánh giá sơ bộ các góc định hướng, góc tư thế bằng cách lấy trung bình 
các giá trị của cảm biến quán tính IMU. 
Kỹ thuật điều khiển 
 74 V. H. Hà, H. S. Dương, C. Đ. Sáng, “Về một phương pháp xác định  đối tượng xe cơ giới.” 
- Giai đoạn 2: Xác định tinh (5-15 phút); 
Mục đích: Sàng lọc các góc định hướng bằng thuật toán ước lượng động [3]. 
2.1. Giai đoạn xác định thô 
Như ta đã biết ma trận cosin chỉ hướng b
nC là ma trận chuyển hệ tọa độ dẫn đường 
OXnYnZn sang hệ tọa độ liên kết OXbYbZb: 
[XbYbZb]= bnC [XnYnZn] (1) 
cos cos cos sin sin
sin sin cos cos sin sin sin sin cos cos sin cos
cos sin cos sin sin cos sin sin sin cos cos cos
b
nC
    
           
           
− 
 = − +
 + − 
(2) 
Theo đó, có thể xác định vecto trọng lực trên hệ tọa độ gắn liền như sau: 
0
0 0
0 0
0 sin
0 sin cos
cos cos
b n
X X
b b n b
Y n Y n
b n
Z Z
G G g
G C G C g
G G g g

 
 
 − 
 = = = 
(3) 
Trong đó, b b b
X Y ZG G G là các giá đo được bằng gia tốc kế từ đó có thể xác định được các 
góc pitch θ0, roll ϕ0 ban đầu từ phương trình (6): 
( )
0
2 2
0
arctan ;
( ) ( )
arctan
b
X
b b
Y Z
b
Y
b
Z
G
G G
G
G


− =
 +
= 
(4) 
Để xác định sơ bộ góc hướng ban đầu phải sử dụng dữ liệu của con quay gyroscope 
dựa theo biểu thức sau: 
b n
X X
b b n
X n Y
b n
X Z
C
 
 
 
= 
(5) 
b b b
X Y Z   là các giá trị vận tốc góc đo được từ gyroscope. Trong trường hợp xác định 
tư thế ban đầu khi vật thể đứng yên hình chiếu vecto vận tốc góc quay của trái đất trên hệ 
tọa độ dẫn đường là các giá trị n n n
X Y Z   được tính theo công thức: 
cos
0
sin
n
X e
n
Y
n
Z e
  

  
=
=
= −
 (6) 
Trong đó: φ là vĩ độ tại điểm đặt của vật thể; 
 ωe = 7.292*10-5 rad/s là vận tốc góc quay của trái đất; 
 g là gia tốc trọng trường tại điểm O. 
Từ phương trình (5) và (6) kết hợp ma trận cosin định hướng có thể xác định sơ bộ 
góc hướng (heading) ψ0 theo công thức sau: 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 75 
0 0 0
0
0
0
0 0
0
0 0
cos cos ( sin );
sin
cos ;
cos
sin sin sin
arccos arccos .
cos cos cos
b n n
X X Z
b n
X Y
n
X
b n b
X Z X e
n
X e
     
  

 
     

   
= + −
+
=
+ −
= =
(7) 
Để xử lý tín hiệu đầu ra từ IMU nhóm nghiên cứu sử dụng bộ lọc trước. Nó bao gồm 
bộ lọc thông thấp Infinite Impulse Response (IIR) với chức năng giảm nhiễu tần số cao 
sau đó đầu ra của IIR được mô hình hóa và bộ lọc Kalman 2 trạng thái được sử dụng để 
giảm nhiễu hơn nữa. Đầu ra cảm biến của con quay sợi quang FOG sẽ bị ảnh hưởng bởi 
nhiễu rất lớn, ví dụ như khi hệ thống được đặt trên một chiếc xe có động cơ đang bật, 
phương sai nhiễu ồn sẽ tăng lên rất nhiều. Khi đó sử dụng bộ lọc IIR có thể hạn chế 
nhiễu tần số cao. Tuy nhiên, trong việc căn chỉnh tần số cắt của IIR không thể đặt quá 
thấp để tránh việc thông tin hữu ích sẽ mất và kết quả được lọc có thể bị sai lệch [5]. 
Trong hệ thống của chúng tôi, bộ lọc IIR 4 bậc với tần số cắt 10 Hz được thiết kế [6] do 
các phương tiện mặt đất chuyển động với tần số thấp (từ 0-5Hz). Hệ số bộ lọc IIR được 
chọn như sau: b0=0.0048423; b1=0.0192974; b2=0.0289461; b3=0.0192984; 
b4=0.0048243; a1=-2.369513; a2= 2.3139884; a3=-1.0546654; a4=0.1873795. 
Hình ảnh tín hiệu gyroscope trước và sau bộ lọc thể hiện như hình 4. 
Hình 4. Đầu ra của gyroscope trước và sau bộ lọc. 
2.2. Giai đoạn xác định tinh tư thế của SINS gắn trên đối tượng đứng yên 
Căn chỉnh thô dựa trên sự lý tưởng hóa trong đó không có lỗi gia tốc kế và con quay 
hồi chuyển. Nhưng thực tế dữ liệu gia tốc và dữ liệu đầu ra của con quay đều có lỗi, đặc 
biệt là con quay hồi chuyền có thể có trôi lớn. Vì vậy, ma trận trạng thái hay các góc 
Euler được đưa ra bởi căn chỉnh thô có thể có một số lỗi. Với căn chỉnh thô có thể đo các 
góc roll và pitch với sai số 0,010 hoặc tốt hơn, tuy nhiên, với góc hướng ( - heading) 
sai số đưa ra có thể là rất lớn. 
Căn chỉnh chính xác được thực hiện trên cơ sở căn chỉnh thô và góc lệch giữa hệ tọa 
độ điều hướng và hệ tọa độ điều hướng thực được điều chỉnh để làm cho nó càng gần 0 
càng tốt. Để đạt được ước lượng trạng thái ban đầu chính xác hơn, các phép đo liên tiếp 
được sử dụng để thực hiện tự liên kết trong một khoảng thời gian. Trong điều kiện chuẩn 
tinh, các phép đo vận tốc bằng không được sử dụng trong bộ lọc Kalman trong giai đoạn 
căn chỉnh ban đầu để hiệu chỉnh vận tốc và trạng thái góc tư thế. Ở đây, mô hình sai số 
góc các góc tư thế ψN,E,D được xét đến với giả định bias của cảm biến được mô hình hóa 
trong khung điều hướng là không thay đổi. Mô hình trạng thái của hệ thống [6] có thể 
Kỹ thuật điều khiển 
 76 V. H. Hà, H. S. Dương, C. Đ. Sáng, “Về một phương pháp xác định  đối tượng xe cơ giới.” 
được viết như sau: 
0 2 0 0 1 0 0 0 0
2 0 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
N eD
E eD
N eD
E eD eN
D eN
N
E
N
E
D
g
g
 
 
 
  
 



 − − 
− 
 = 
  
  
N
E
N
E
D
k
N
E
N
E
D
w








 + 
 
 
(8) 
Trong đó,  là bias của gia tốc kế, ε độ trôi của gyroscope. Phương trình 8 có thể viết 
lại dưới dạng như sau: 
1 1 1k k k kx F x w− − −= + (9) 
Xk là trạng thái tại thời điểm k, Fk-1 biểu thị ma trận chuyển trạng thái, wk-1 biểu thị 
nhiễu quá trình (thường là nhiễu trắng Gaussian) với mật độ phổ công suất Q. 
q ~ ( ) 2 2 2 2 20, , , , , , ,0,0,0,0,0a a g g gN Q Q diag q q q q q = (10) 
Trong đó, qa đại diện cho nhiễu ngẫu nhiên của gia tốc kế và qg là nhiễu ngẫu nhiên 
của con quay hồi chuyển. 
Khi xe ở trạng thái đứng yên, thông tin vận tốc bằng 0 trong khung điều hướng được 
sử dụng làm tham chiếu bên ngoài và vector đo có thể được xây dựng như: 
( ) ( )
( ) ( )
0
0
N INS N REAL N N
E INS E REAL E E
v v v v
Z
v v v v


− − 
= = 
− − 
 (11) 
Trong đó, vN và vE là vận tốc phương ngang của xe được tính bởi SINS. Như vậy, vận 
tốc đầu ra của SINS chính là sai số vận tốc và nó có thể được coi là vectơ đo hay vector 
quan sát. Khi đó, phương trình đo lường của hệ thống [7, 8] được biểu diễn như phương 
trình sau: 
( )
1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0
k k k k
N
E
Z H x
x t
v
v


= + 
=
+
 (12) 
Trong đó: Zk là vector đo hay vector quan sát; Hk là ma trận đo hay ma trạn quan sát, 
vk biểu thị nhiễu đo với mật độ phổ công suất R. 
r ~ ( )  0, , ,N R R diag R R = (13) 
Bộ lọc Kalman vòng kín (hình 5) 10 trạng thái được triển khai để thực hiện ước lượng 
và hiệu chỉnh các tham số điều hướng, khoảng thời gian tính toán của bộ lọc Kalman là 
0.1s. Hệ thống dẫn đường quán tính sử dụng khối đo lường quán tính IMU500 của hãng 
Optolink-Nga. Độ trôi của con quay hồi chuyển sợi quang (Fiber-Optic Gyroscope – 
FOG) là 0,10/h, turn-on drift với phương sai Allan là 0.0050/h, nhiễu ngẫu nhiên của 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 77 
FOG là 20/h. Độ trôi ngẫu nhiên của gia tốc kế là 20μg và sai số ngẫu nhiên là 0.5mg. 
Các ma trận hiệp phương sai được thiết lập như sau: 
2 2 2 2 2 2 2 0 2 0 2 0 2
2 2 0 2 0 2 0 2
2 2
(0.3 / ) , (0.3 / ) , (1) , (1) , ( ) , (20 ) , (20 ) , (0.1 / ) , (0.1 / ) , (0.1 / )
(0.5 ) , (0.5 ) , (0.005 / ) , (0.005 / ) , (0.005 / ,0,0,0,0,
2
)
(0.00 5 / ) , (0.0025 /
0
)
DP diag m s m s P g g h h h
mg mg h h hQ
m
diag
R diag s m s
 
 = 
 = 
 = 
SINS
Zero-velocity
Kalman Filter
v=0
vINS
Ước lượng lỗi quán tính
Tư thế đầu ra sau hiệu chỉnh
Hình 5. Bộ lọc Kalman vòng kín cho xác định tư thế ban đầu của SINS. 
3. THỬ NGHIỆM VÀ KẾT QUẢ 
Trên cơ sở hệ dẫn đường quán tính ta xây dựng cấu hình phần cứng bộ thử nghiệm 
gồm các thành phần sau: khối đo lường quán tính IMU500, module nguồn cách ly, bo 
mạch xử lý DSP và module giao tiếp (hình 6). 
Hình 6. Phần cứng bộ thiết bị thử nghiệm. 
Kết quả thử nghiệm xác định góc tư thế ban đầu ở hai vị trí 89B Lý Nam Đế và 147 
Phú Viên được thể hiện như trên hình 7, 8 và trên bảng 1. 
Hình 7. Kết quả thử nghiệm xác định góc phương vị tại vị trí 1. 
Kỹ thuật điều khiển 
 78 V. H. Hà, H. S. Dương, C. Đ. Sáng, “Về một phương pháp xác định  đối tượng xe cơ giới.” 
Hình 8. Kết quả thử nghiệm xác định góc phương vị tại vị trí 2. 
Kết quả góc phương vị ban đầu của khối dẫn đường quán tính sử dụng con quay hồi 
chuyển sợi quang IMU500. 
Bảng 1. Kết quả căn chỉnh góc phương vị ban đầu tại các vị trí thử nghiệm. 
STT Vị trí 1 (89B Lý Nam Đế) Ví trí 2 (147 Phú Viên) 
Ψ0 (Độ) Ψ0 (Độ) 
1 10.01 -28.82 
2 10.03 -28.83 
3 10.04 -28.86 
4 10.05 -28.82 
5 10.01 -28.84 
6 10.04 -28.85 
7 10.03 -28.86 
8 10.04 -28.83 
9 10.05 -28.87 
10 10.02 -28.85 
Qua số liệu từ bảng kết quả căn chỉnh tại các vị trí khác nhau và đồ thị thu được từ 
giao diện phần mềm thu thập và hiển thị số liệu có thể thấy thông qua bước căn chỉnh thô 
có thể tính toán sơ bộ các góc tư thế, từ đó làm giảm phương sai ước tính ban đầu và 
tăng tốc độ hội tụ khi xác định góc hướng. Cũng qua thí nghiệm khi vật thể đứng yên, 
việc ước lượng được độ trôi bias drift góc hướng đã đạt 0.1độ/h tương đương với chỉ tiêu 
của nhà sản xuất. 
4. KẾT LUẬN 
Như vậy, trong thuật toán căn chỉnh góc tư thế ban đầu, việc xác định sơ bộ các góc 
giúp tăng tốc độ hội tụ của bộ lọc Kalman trong gian đoạn căn chỉnh tinh, các góc roll ϕ0 
và pitch θ0 ở thời điểm đối tượng đứng yên được xác định trực tiếp thông qua các giá trị 
đo của gia tốc kế và sai số cũng phụ thuộc vào sai số của gia tốc kế nên có độ chính xác 
khá cao, giá trị ổn định không gặp hiện tượng trôi như con quay hồi chuyển. Việc triệt 
tiêu nhiễu của các cảm biến trong môi trường thực được xử lý thông qua bộ lọc trước gồm 
2 thành phần bộ lọc thông thấp IIR và bộ lọc Kalman 2 trạng thái. Ngoài ra, có thể thấy 
rằng phương sai ước tính ban đầu của sai số góc phương vị là yếu tố chính ảnh hưởng đến 
tốc độ hội tụ của sai số góc phương vị. Bằng cách điều chỉnh nó, lỗi góc phương vị sẽ 
sớm hội tụ và vấn đề lỗi góc phương vị lớn có thể được giải quyết. Tính đúng đắn và khả 
thi của thuật toán được xác minh bằng mô phỏng và qua thử nghiệm thực tế. 
Bài báo này đã được báo cáo tại Hội thảo Quốc gia: Ứng dụng Công nghệ cao vào thực tiễn – 60 
năm phát triển Viện KH-CN quân sự. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 79 
TÀI LIỆU THAM KHẢO 
[1]. H. W. Park, J. G. Lee, and C. G. Park, “Covariance analysis of strapdown INS considering 
gyrocompass characteristics,” IEEE Transactions on Aerospace and Electronic Systems, 
vol. 31, no. 1, pp. 320–328, 1995. 
[2]. Мелешко, В.В. “Бесплатформенные инерциальные навигационные системы: учебное 
пособие”/ В.В. Мелешко, О.И. Нестеренко. – Кировоград: Полимед-Сервис, 2011. – 171с. 
[3]. Голован А. А., Парусников Н. А. “Математические основы навигационных систем”. 
М.: Моск. гос. университет, 2010. Т. 1–3. 
[4]. Бромберг П. В. “Теория инерциальных систем навигации”/ П. В. Бромберг – М.: 
Наука, 1980. – 296 с. 
[5]. J.G. Proakis, D.G. Manolakis, “Digital Signal Processing: Principles, Algorithms, and 
Applications”, third ed., Prentice-Hall, Englewood Cliffs, NJ, 1996. 
[6]. Shaolin Lu, Ling Xie, Jiabin Chen. “New techniques for initial alignment of strapdown 
inertial navigation system”. Journal of the Franklin Institute 346 (2009) 1021–1037. 
[7]. Liu M, Gao Y, Li G, Guang X, Li S. “An Improved Alignment Method for the Strapdown 
Inertial Navigation System (SINS)”. Sensors (Basel). 2016;16(5):621. Published 2016 Apr 
29. doi:10.3390/s16050621 
[8]. Feng Sun, Tong Cao, Bo Xu, Yueyang Ben and Yudan Wang. “Initial Alignment for Strapdown 
Inertial Navigation System Based on Inertial Frame”. Proceedings of the 2009 IEEE. 
International Conference on Mechatronics and Automation. August 9-12, Changchun, China. 
ABSTRACT 
A METHOD OF DETERMINING THE INITIAL ATTITUDE ANGLES 
FOR THE STRAPDOWN INERTIAL NAVIGATION SYSTEM 
IN GYROCOMPASS MODE ON THE MOTOR VEHICLES 
For the strapdown inertial navigation system, determining the exact angle of the initial 
attitudes plays an extremely important role, directly affecting the later navigation process 
of the system. The paper deals with the initial alignment determination algorithm 
including true NORTH for the SINS on non-moving objects in gyrocompass mode. The 
algorithm is carried out in two stages: determining the preliminary initial posture and 
determining the correct initial posture based on the state vectors of the IMU inertial 
measurement unit. The results obtained proved the accuracy of the algorithm. 
Keywords: Alignment; SINS; IMU; Euler angles; Gyrocompass. 
Nhận bài ngày 28 tháng 7 năm 2020 
Hoàn thiện ngày 10 tháng 12 năm 2020 
 Chấp nhận đăng ngày 15 tháng 12 năm 2020 
Địa chỉ: Viện Tự động hóa KTQS/ Viện Khoa học và Công nghệ quân sự. 
 *Email: vuhatdh@gmail.com.