Ứng dụng thuật toán học máy trong ước lượng mô hình suy hao truyền sóng dải sóng milimet

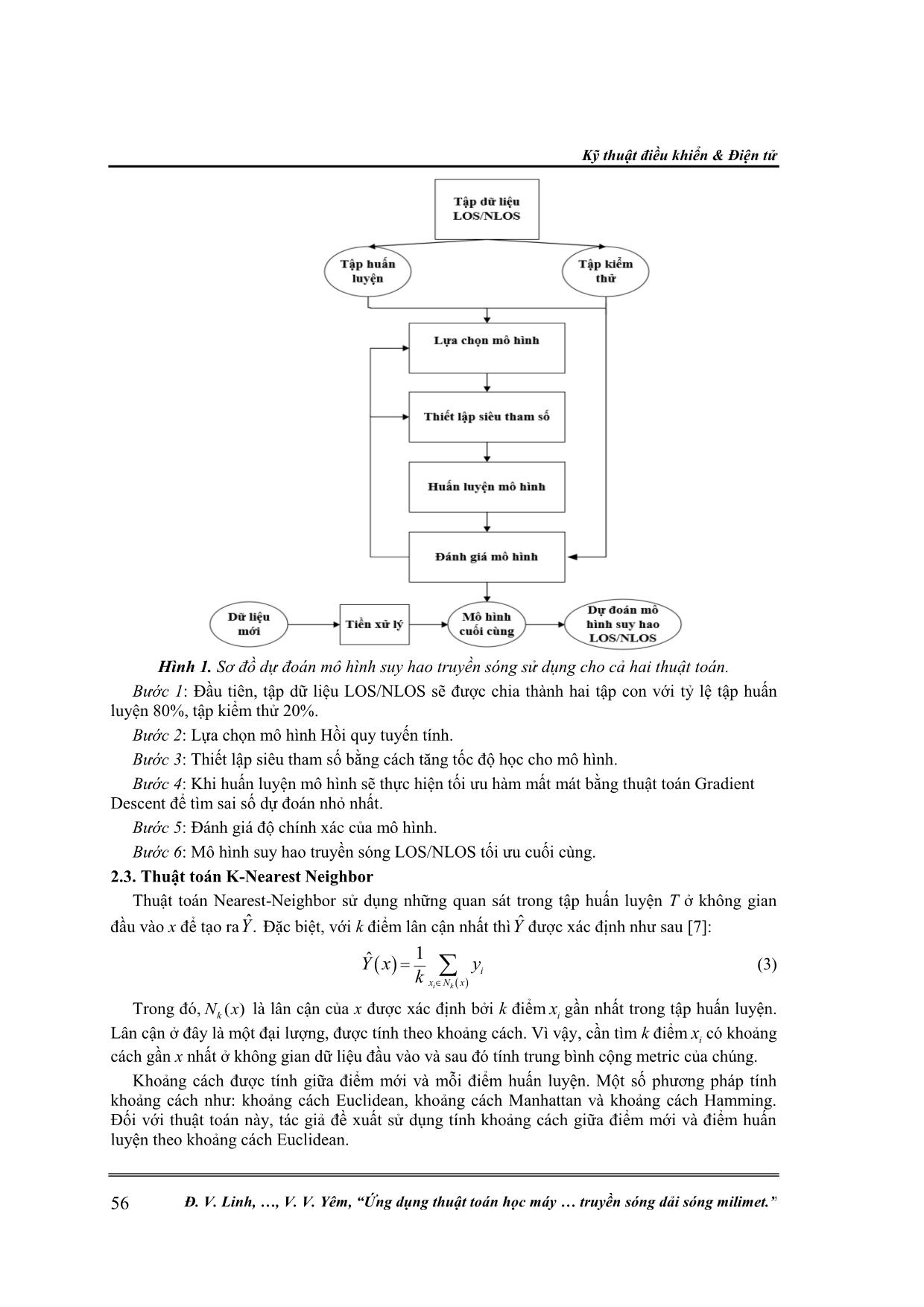
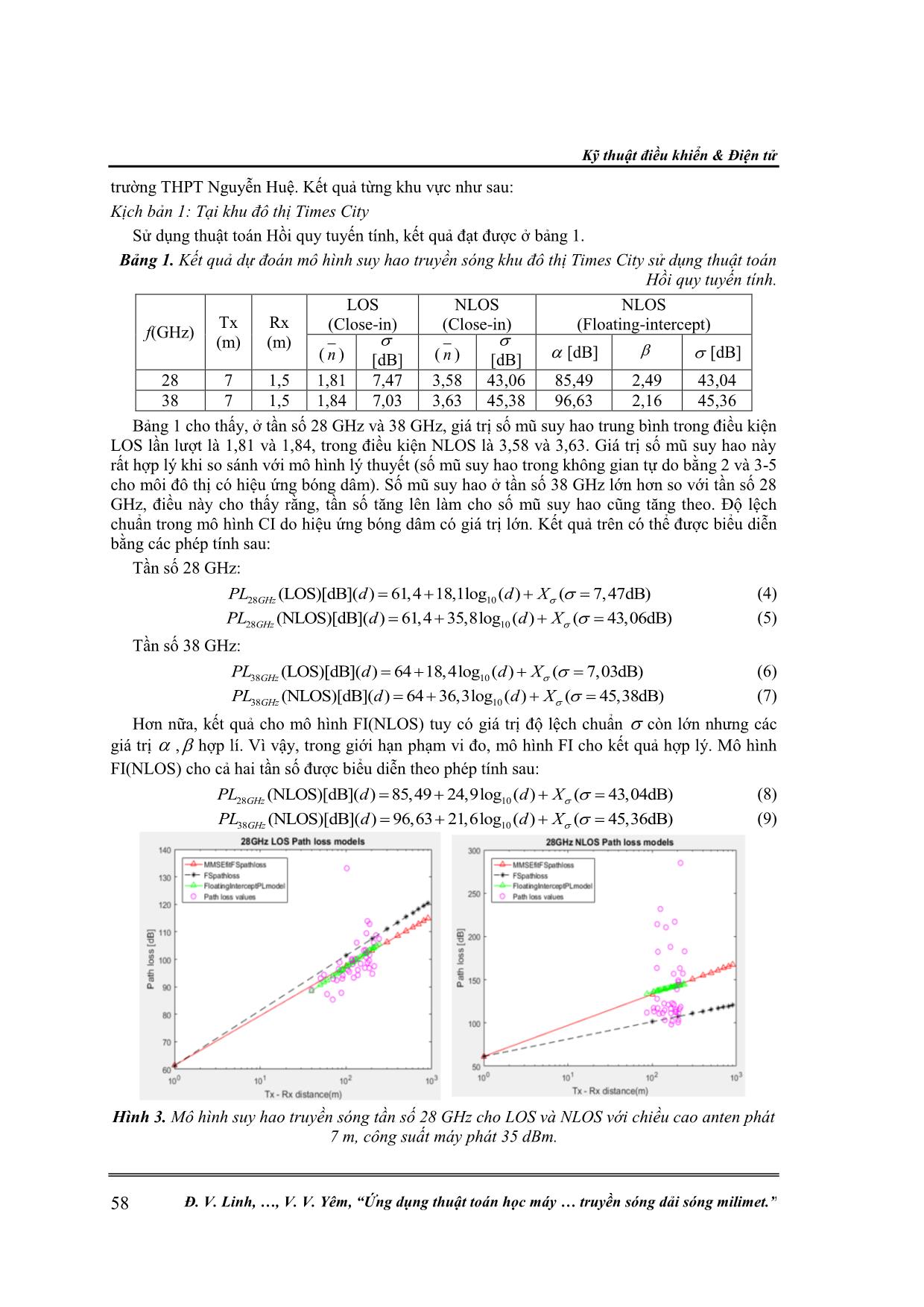
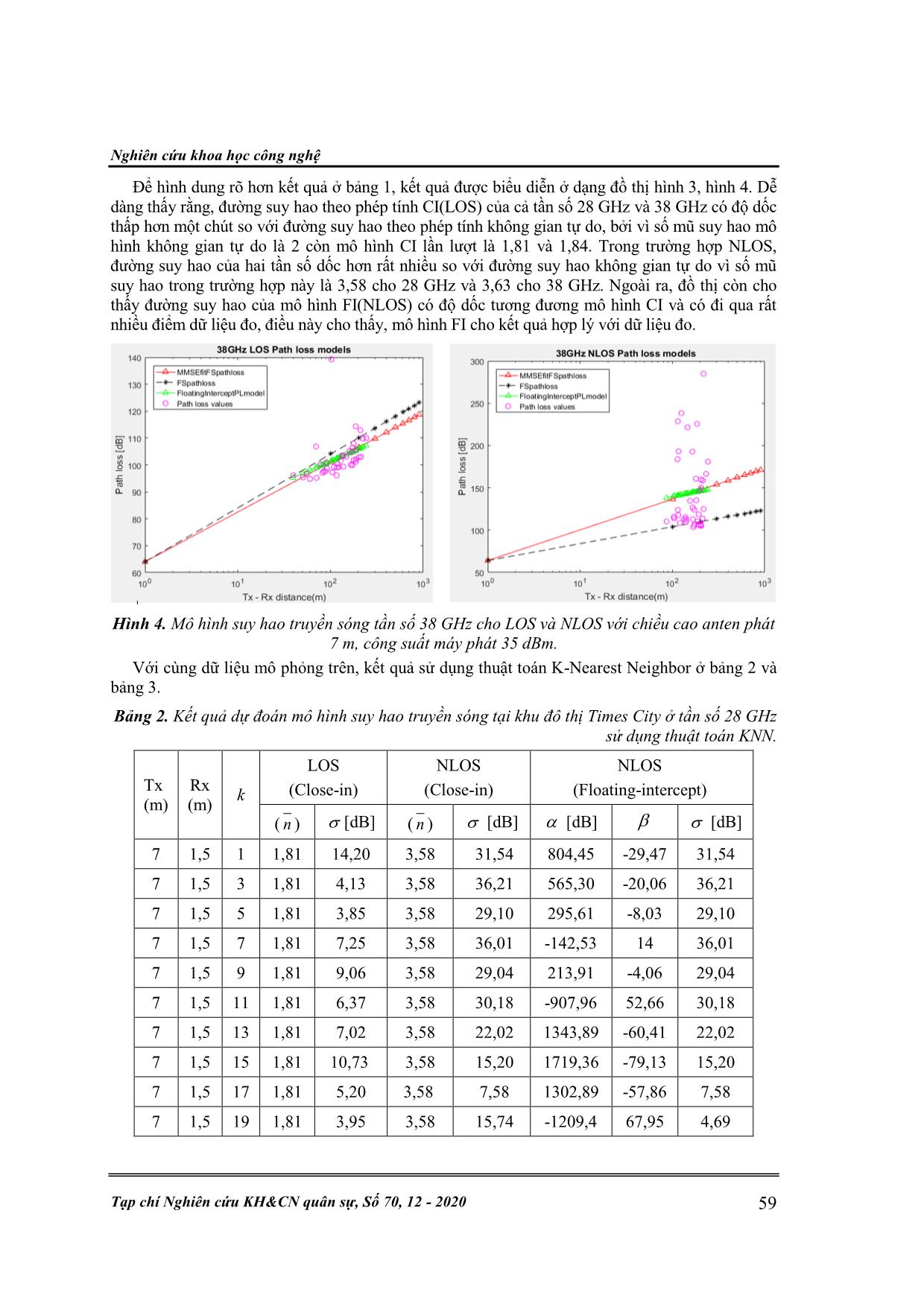
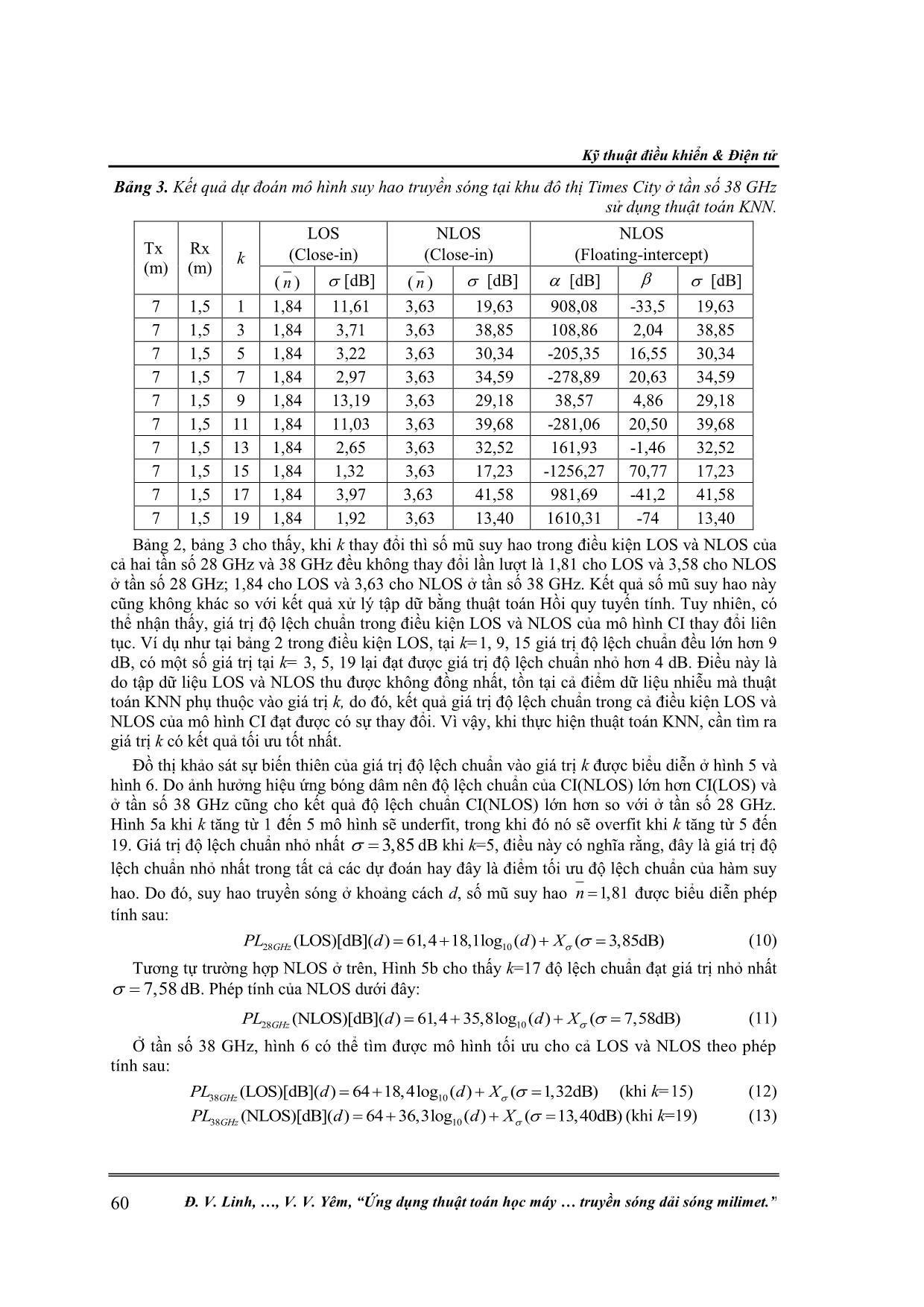
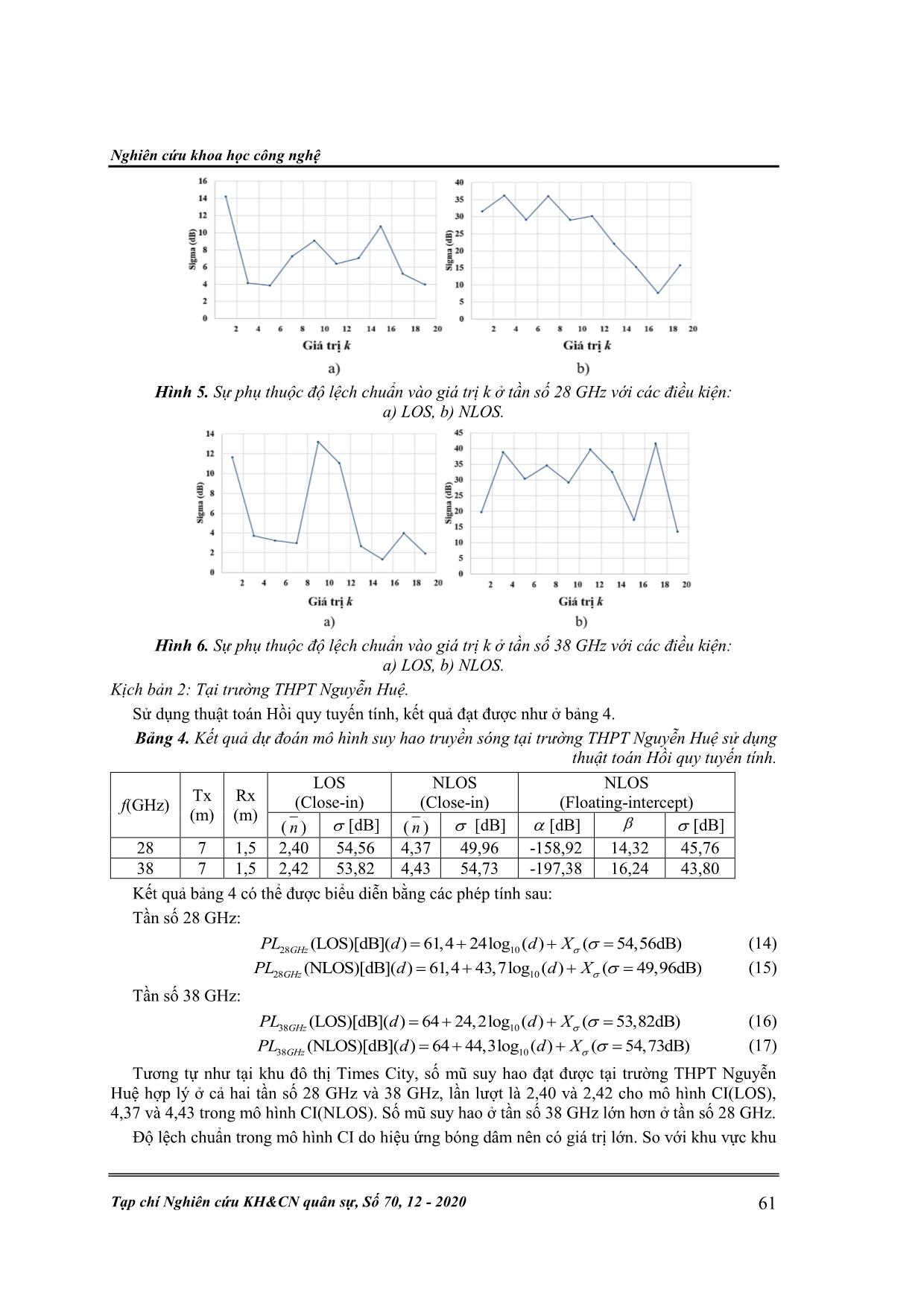
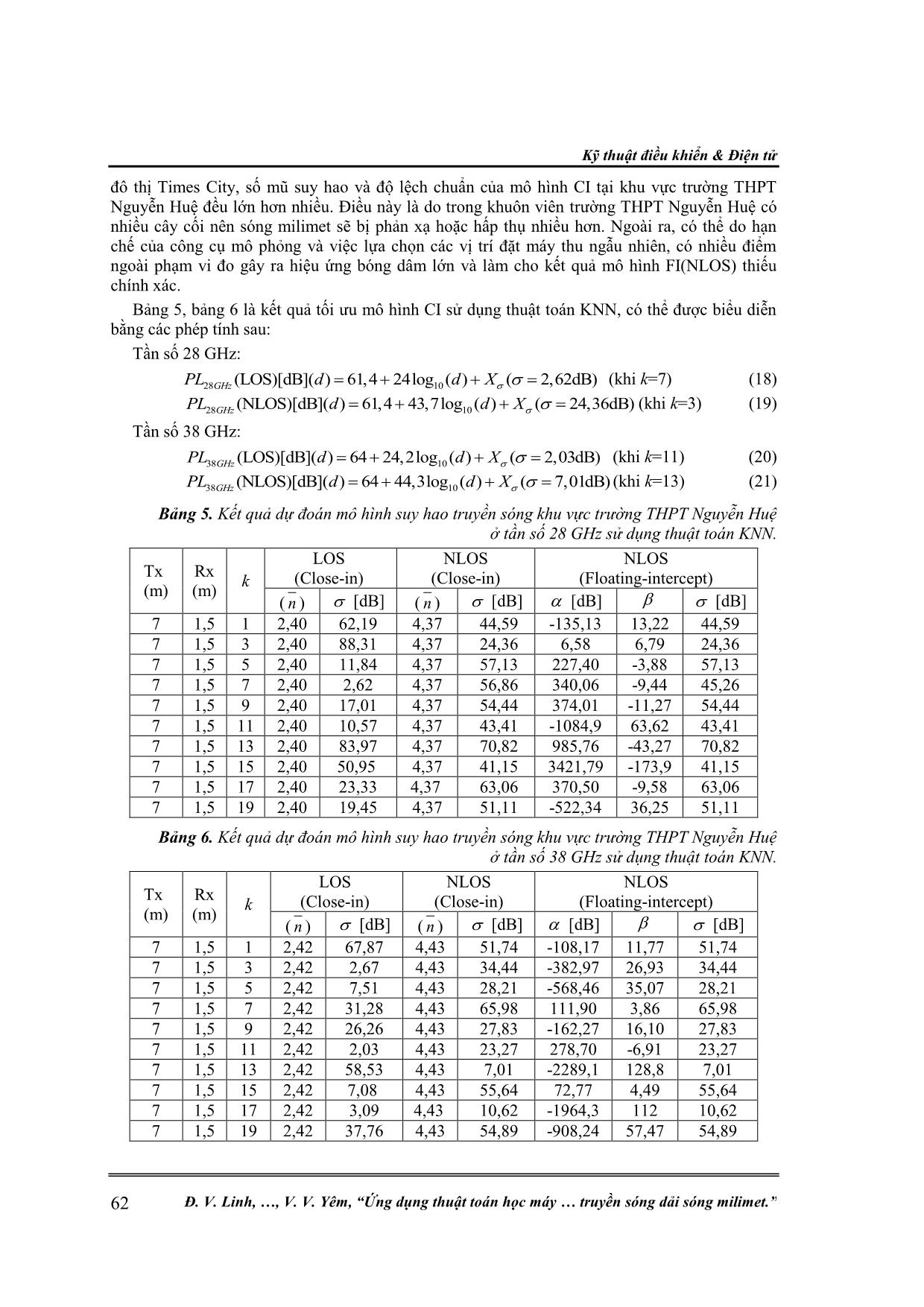
Kỹ thuật điều khiển & Điện tử 
 54 Đ. V. Linh, , V. V. Yêm, “Ứng dụng thuật toán học máy  truyền sóng dải sóng milimet.” 
ỨNG DỤNG THUẬT TOÁN HỌC MÁY TRONG ƯỚC LƯỢNG 
MÔ HÌNH SUY HAO TRUYỀN SÓNG DẢI SÓNG MILIMET 
Đinh Văn Linh1, Đỗ Cao Khánh1, Vũ Thanh Quang2, Vũ Văn Yêm2* 
Tóm tắt: Trong bài báo này, chúng tôi sẽ phát triển và ứng dụng thuật toán trong Học 
máy đó là Hồi quy tuyến tính và thuật toán K-Nearest Neighbor để dự đoán mô hình suy 
hao truyền sóng dải sóng milimet. Dữ liệu mô phỏng thu được từ phần mềm Wireless 
Insite, với kịch bản một máy phát và nhiều máy thu được đặt nhẫu nhiên tại các vị trí 
trong tầm nhìn thẳng (Line-of-Sight) và không trong tầm nhìn thẳng (Non-line-of-sight). 
Phương pháp đề xuất được áp dụng để cải thiện và điều chỉnh mô hình suy hao truyền 
sóng tần số 28 GHz và 38 GHz tại khu đô thị Times City và trường THPT Nguyễn Huệ. 
Kết hợp cả hai thuật toán này vào việc xây dựng mô hình suy hao truyền sóng dải sóng 
milimet cho kết quả phù hợp khi so sánh với kết quả 3GPP và NYU Wireless, từ đó giúp 
cải thiện kết quả tối ưu mô hình suy hao truyền sóng. 
Từ khóa: K-Nearest Neighbor; Hồi quy tuyến tính; Gradient Descent; 5G; Dải sóng milimet; Mô hình suy hao. 
1. MỞ ĐẦU 
Hệ thống thông tin di động 5G sử dụng dải sóng milimet đang được rất nhiều công ty cũng 
như các nhà nghiên cứu quan tâm. Trong hệ thống 5G, giao diện vô tuyến đặc biệt là băng tần sử 
dụng có nhiều thách thức cần phải giải quyết. Qua nhiều nghiên cứu, dải sóng milimet với tần số 
28 GHz và 38 GHz đang là những tần số tiềm năng cho hệ thống 5G. 
Dự đoán mô hình suy hao truyền sóng trong kênh sóng milimet (mmWave) rất quan trọng cho 
việc thiết kế hệ thống và ước lượng vùng phủ sóng và dung lượng mạng không dây siêu băng 
rộng [1, 2]. Mô hình suy hao truyền sóng dải tần số 28 GHz và 73 GHz đã công bố dựa trên tập 
dữ liệu thí nghiệm tại thành phố New York sử dụng kết hợp cả hai mô hình truyền thống, đó là, 
mô hình tham chiếu theo không gian tự do Close-in và mô hình hồi quy bình phương tối thiểu 
Floating-intercept để dự đoán mô hình suy hao truyền sóng cho hai dạng Line-of-Sight (LOS) và 
Non-Line-of-Sight (NLOS) [3]. 
Học máy là một phương pháp dựa vào tập dữ liệu mở lớn và kiến trúc mô hình linh hoạt để đưa 
ra dự đoán. Gần đây, Học máy được sử dụng rộng rãi trong nhiều lĩnh vực như xe tự lái, khai thác 
dữ liệu, nhận dạng giọng nói, Học máy có thể được phân thành hai loại là học giám sát và học 
không giám sát, phụ thuộc vào mẫu dữ liệu có nhãn hoặc không. Đối với dự đoán suy hao, đây là 
vấn đề hồi quy giám sát, vì vậy, nó có thể được giải quyết bằng thuật toán học máy giám sát như 
mạng nơ ron nhân tạo, hồi quy vectơ hỗ trợ, và cây quyết định. Nghiên cứu đã chỉ ra rằng, mô hình 
dựa vào học máy chính xác hơn mô hình thực nghiệm và hiệu quả tính toán lớn hơn so với mô hình 
xác định [4, 5]. Trong bài báo này, chúng tôi nghiên cứu và đề xuất hai thuật toán học máy cho mô 
hình suy hao có tên là Hồi quy tuyến tính và K-Nearest Neighbor (KNN). Thuật toán Hồi quy 
tuyến tính thường được dùng để dự đoán biến phụ thuộc (Y) vào biến độc lập (X) trong trường hợp 
mô hình là một hàm tuyến tính, trong khi đó, thuật toán KNN sử dụng trung bình trọng số của k 
điểm gần nhất, trọng số được tính bằng nghịch đảo khoảng cách của chúng, thuật toán này sử dụng 
những đặc tính tương tự nhau để dự đoán giá trị của bất kì điểm dự liệu mới nào. 
Bài báo này được phân bố theo các phần sau. Phần 2 mô tả mô hình suy hao truyền sóng dải 
sóng milimet và bước thực hiện dự đoán mô hình suy hao dựa vào thuật toán Hồi quy tuyến tính 
và K-Nearest Neighbor đối với dữ liệu thu thập từ mô hình mô phỏng khu vực truyền sóng. Phần 
3 là một số kết quả đạt được sau khi mô phỏng mô hình truyền sóng tần số 28 GHz và 38 GHz 
tại khu vực khu đô thị Times City và Trường THPT Nguyễn Huệ áp dụng các thuật toán Học 
máy đã đề xuất. Kết quả sẽ so sánh với kết quả của 3GPP và NYU Wireless. Cuối cùng, một vài 
kết luận nêu ra ở phần 4. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 70, 12 - 2020 55 
2. MÔ HÌNH SUY HAO TRUYỀN SÓNG VÀ ỨNG DỤNG THUẬT TOÁN HỌC MÁY 
ĐỂ XÂY DỰNG MÔ HÌNH SUY HAO TRUYỀN SÓNG DẢI SÓNG MILIMET 
2.1. Mô hình suy hao truyền sóng dải sóng milimet 
Mô hình suy hao truyền sóng tại một khoảng cách d (m) được ước lượng bằng cách sử dụng 
mô hình tham chiếu theo không gian tự do Close-in (CI) như sau [6]: 
0
10 10 0
0
4
[dB]( ) 20log 10 log ( )
d d
PL d n X d d
d


 (1) 
Trong đó, 
0d là khoảng cách tham chiếu không gian tự do, (m) bước sóng mang, n số mũ 
suy hao phụ thuộc vào môi trường truyền sóng, X biến xác suất ngẫu nhiên thể hiện hiệu ứng 
bóng dâm với giá trị trung bình 0 dB và độ lệch chuẩn  , d (m) khoảng cách Tx-Rx. Trong 
nghiên cứu này, tác giả chọn khoảng cách tham chiếu 
0 1m.d 
Mô hình Floating-intercept (FI) đang được sử dụng trong một số tiêu chuẩn như 3GPP và 
WINNER II, công thức biểu diễn như sau [3]: 
10[dB]( ) 10 log  ... Close-in) 
NLOS 
(Close-in) 
NLOS 
(Floating-intercept) 
( n )  [dB] ( n )  [dB] [dB]   [dB] 
7 1,5 1 1,81 14,20 3,58 31,54 804,45 -29,47 31,54 
7 1,5 3 1,81 4,13 3,58 36,21 565,30 -20,06 36,21 
7 1,5 5 1,81 3,85 3,58 29,10 295,61 -8,03 29,10 
7 1,5 7 1,81 7,25 3,58 36,01 -142,53 14 36,01 
7 1,5 9 1,81 9,06 3,58 29,04 213,91 -4,06 29,04 
7 1,5 11 1,81 6,37 3,58 30,18 -907,96 52,66 30,18 
7 1,5 13 1,81 7,02 3,58 22,02 1343,89 -60,41 22,02 
7 1,5 15 1,81 10,73 3,58 15,20 1719,36 -79,13 15,20 
7 1,5 17 1,81 5,20 3,58 7,58 1302,89 -57,86 7,58 
7 1,5 19 1,81 3,95 3,58 15,74 -1209,4 67,95 4,69 
Kỹ thuật điều khiển & Điện tử 
 60 Đ. V. Linh, , V. V. Yêm, “Ứng dụng thuật toán học máy  truyền sóng dải sóng milimet.” 
Bảng 3. Kết quả dự đoán mô hình suy hao truyền sóng tại khu đô thị Times City ở tần số 38 GHz 
sử dụng thuật toán KNN. 
Tx 
(m) 
Rx 
(m) 
k 
LOS 
(Close-in) 
NLOS 
(Close-in) 
NLOS 
(Floating-intercept) 
( n )  [dB] ( n )  [dB] [dB]   [dB] 
7 1,5 1 1,84 11,61 3,63 19,63 908,08 -33,5 19,63 
7 1,5 3 1,84 3,71 3,63 38,85 108,86 2,04 38,85 
7 1,5 5 1,84 3,22 3,63 30,34 -205,35 16,55 30,34 
7 1,5 7 1,84 2,97 3,63 34,59 -278,89 20,63 34,59 
7 1,5 9 1,84 13,19 3,63 29,18 38,57 4,86 29,18 
7 1,5 11 1,84 11,03 3,63 39,68 -281,06 20,50 39,68 
7 1,5 13 1,84 2,65 3,63 32,52 161,93 -1,46 32,52 
7 1,5 15 1,84 1,32 3,63 17,23 -1256,27 70,77 17,23 
7 1,5 17 1,84 3,97 3,63 41,58 981,69 -41,2 41,58 
7 1,5 19 1,84 1,92 3,63 13,40 1610,31 -74 13,40 
Bảng 2, bảng 3 cho thấy, khi k thay đổi thì số mũ suy hao trong điều kiện LOS và NLOS của 
cả hai tần số 28 GHz và 38 GHz đều không thay đổi lần lượt là 1,81 cho LOS và 3,58 cho NLOS 
ở tần số 28 GHz; 1,84 cho LOS và 3,63 cho NLOS ở tần số 38 GHz. Kết quả số mũ suy hao này 
cũng không khác so với kết quả xử lý tập dữ bằng thuật toán Hồi quy tuyến tính. Tuy nhiên, có 
thể nhận thấy, giá trị độ lệch chuẩn trong điều kiện LOS và NLOS của mô hình CI thay đổi liên 
tục. Ví dụ như tại bảng 2 trong điều kiện LOS, tại k=1, 9, 15 giá trị độ lệch chuẩn đều lớn hơn 9 
dB, có một số giá trị tại k= 3, 5, 19 lại đạt được giá trị độ lệch chuẩn nhỏ hơn 4 dB. Điều này là 
do tập dữ liệu LOS và NLOS thu được không đồng nhất, tồn tại cả điểm dữ liệu nhiễu mà thuật 
toán KNN phụ thuộc vào giá trị k, do đó, kết quả giá trị độ lệch chuẩn trong cả điều kiện LOS và 
NLOS của mô hình CI đạt được có sự thay đổi. Vì vậy, khi thực hiện thuật toán KNN, cần tìm ra 
giá trị k có kết quả tối ưu tốt nhất. 
Đồ thị khảo sát sự biến thiên của giá trị độ lệch chuẩn vào giá trị k được biểu diễn ở hình 5 và 
hình 6. Do ảnh hưởng hiệu ứng bóng dâm nên độ lệch chuẩn của CI(NLOS) lớn hơn CI(LOS) và 
ở tần số 38 GHz cũng cho kết quả độ lệch chuẩn CI(NLOS) lớn hơn so với ở tần số 28 GHz. 
Hình 5a khi k tăng từ 1 đến 5 mô hình sẽ underfit, trong khi đó nó sẽ overfit khi k tăng từ 5 đến 
19. Giá trị độ lệch chuẩn nhỏ nhất 3,85 dB khi k=5, điều này có nghĩa rằng, đây là giá trị độ 
lệch chuẩn nhỏ nhất trong tất cả các dự đoán hay đây là điểm tối ưu độ lệch chuẩn của hàm suy 
hao. Do đó, suy hao truyền sóng ở khoảng cách d, số mũ suy hao 1,81n được biểu diễn phép 
tính sau: 
28 10(LOS)[dB]( ) 61,4 18,1log ( ) ( 3,85dB)GHzPL d d X  (10) 
Tương tự trường hợp NLOS ở trên, Hình 5b cho thấy k=17 độ lệch chuẩn đạt giá trị nhỏ nhất
7,58 dB. Phép tính của NLOS dưới đây: 
28 10(NLOS)[dB]( ) 61,4 35,8log ( ) ( 7,58dB)GHzPL d d X  (11) 
Ở tần số 38 GHz, hình 6 có thể tìm được mô hình tối ưu cho cả LOS và NLOS theo phép 
tính sau: 
38 10(LOS)[dB]( ) 64 18,4log ( ) ( 1,32dB)GHzPL d d X  (khi k=15) (12) 
38 10(NLOS)[dB]( ) 64 36,3log ( ) ( 13,40dB)GHzPL d d X  (khi k=19) (13) 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 70, 12 - 2020 61 
Hình 5. Sự phụ thuộc độ lệch chuẩn vào giá trị k ở tần số 28 GHz với các điều kiện: 
a) LOS, b) NLOS. 
Hình 6. Sự phụ thuộc độ lệch chuẩn vào giá trị k ở tần số 38 GHz với các điều kiện: 
a) LOS, b) NLOS. 
Kịch bản 2: Tại trường THPT Nguyễn Huệ. 
Sử dụng thuật toán Hồi quy tuyến tính, kết quả đạt được như ở bảng 4. 
Bảng 4. Kết quả dự đoán mô hình suy hao truyền sóng tại trường THPT Nguyễn Huệ sử dụng 
thuật toán Hồi quy tuyến tính. 
f(GHz) 
Tx 
(m) 
Rx 
(m) 
LOS 
(Close-in) 
NLOS 
(Close-in) 
NLOS 
(Floating-intercept) 
( n )  [dB] ( n )  [dB] [dB]   [dB] 
28 7 1,5 2,40 54,56 4,37 49,96 -158,92 14,32 45,76 
38 7 1,5 2,42 53,82 4,43 54,73 -197,38 16,24 43,80 
Kết quả bảng 4 có thể được biểu diễn bằng các phép tính sau: 
Tần số 28 GHz: 
28 10(LOS)[dB]( ) 61,4 24log ( ) ( 54,56dB)GHzPL d d X  (14) 
28 10(NLOS)[dB]( ) 61,4 43,7log ( ) ( 49,96dB)GHzPL d d X  (15) 
Tần số 38 GHz: 
38 10(LOS)[dB]( ) 64 24,2log ( ) ( 53,82dB)GHzPL d d X  (16) 
38 10(NLOS)[dB]( ) 64 44,3log ( ) ( 54,73dB)GHzPL d d X  (17) 
Tương tự như tại khu đô thị Times City, số mũ suy hao đạt được tại trường THPT Nguyễn 
Huệ hợp lý ở cả hai tần số 28 GHz và 38 GHz, lần lượt là 2,40 và 2,42 cho mô hình CI(LOS), 
4,37 và 4,43 trong mô hình CI(NLOS). Số mũ suy hao ở tần số 38 GHz lớn hơn ở tần số 28 GHz. 
Độ lệch chuẩn trong mô hình CI do hiệu ứng bóng dâm nên có giá trị lớn. So với khu vực khu 
Kỹ thuật điều khiển & Điện tử 
 62 Đ. V. Linh, , V. V. Yêm, “Ứng dụng thuật toán học máy  truyền sóng dải sóng milimet.” 
đô thị Times City, số mũ suy hao và độ lệch chuẩn của mô hình CI tại khu vực trường THPT 
Nguyễn Huệ đều lớn hơn nhiều. Điều này là do trong khuôn viên trường THPT Nguyễn Huệ có 
nhiều cây cối nên sóng milimet sẽ bị phản xạ hoặc hấp thụ nhiều hơn. Ngoài ra, có thể do hạn 
chế của công cụ mô phỏng và việc lựa chọn các vị trí đặt máy thu ngẫu nhiên, có nhiều điểm 
ngoài phạm vi đo gây ra hiệu ứng bóng dâm lớn và làm cho kết quả mô hình FI(NLOS) thiếu 
chính xác. 
Bảng 5, bảng 6 là kết quả tối ưu mô hình CI sử dụng thuật toán KNN, có thể được biểu diễn 
bằng các phép tính sau: 
Tần số 28 GHz: 
28 10(LOS)[dB]( ) 61,4 24log ( ) ( 2,62dB)GHzPL d d X  (khi k=7) (18) 
28 10(NLOS)[dB]( ) 61,4 43,7log ( ) ( 24,36dB)GHzPL d d X  (khi k=3) (19) 
Tần số 38 GHz: 
38 10(LOS)[dB]( ) 64 24,2log ( ) ( 2,03dB)GHzPL d d X  (khi k=11) (20) 
38 10(NLOS)[dB]( ) 64 44,3log ( ) ( 7,01dB)GHzPL d d X  (khi k=13) (21) 
Bảng 5. Kết quả dự đoán mô hình suy hao truyền sóng khu vực trường THPT Nguyễn Huệ 
ở tần số 28 GHz sử dụng thuật toán KNN. 
Tx 
(m) 
Rx 
(m) 
k 
LOS 
(Close-in) 
NLOS 
(Close-in) 
NLOS 
(Floating-intercept) 
( n )  [dB] ( n )  [dB] [dB]   [dB] 
7 1,5 1 2,40 62,19 4,37 44,59 -135,13 13,22 44,59 
7 1,5 3 2,40 88,31 4,37 24,36 6,58 6,79 24,36 
7 1,5 5 2,40 11,84 4,37 57,13 227,40 -3,88 57,13 
7 1,5 7 2,40 2,62 4,37 56,86 340,06 -9,44 45,26 
7 1,5 9 2,40 17,01 4,37 54,44 374,01 -11,27 54,44 
7 1,5 11 2,40 10,57 4,37 43,41 -1084,9 63,62 43,41 
7 1,5 13 2,40 83,97 4,37 70,82 985,76 -43,27 70,82 
7 1,5 15 2,40 50,95 4,37 41,15 3421,79 -173,9 41,15 
7 1,5 17 2,40 23,33 4,37 63,06 370,50 -9,58 63,06 
7 1,5 19 2,40 19,45 4,37 51,11 -522,34 36,25 51,11 
Bảng 6. Kết quả dự đoán mô hình suy hao truyền sóng khu vực trường THPT Nguyễn Huệ 
ở tần số 38 GHz sử dụng thuật toán KNN. 
Tx 
(m) 
Rx 
(m) 
k 
LOS 
(Close-in) 
NLOS 
(Close-in) 
NLOS 
(Floating-intercept) 
( n )  [dB] ( n )  [dB] [dB]   [dB] 
7 1,5 1 2,42 67,87 4,43 51,74 -108,17 11,77 51,74 
7 1,5 3 2,42 2,67 4,43 34,44 -382,97 26,93 34,44 
7 1,5 5 2,42 7,51 4,43 28,21 -568,46 35,07 28,21 
7 1,5 7 2,42 31,28 4,43 65,98 111,90 3,86 65,98 
7 1,5 9 2,42 26,26 4,43 27,83 -162,27 16,10 27,83 
7 1,5 11 2,42 2,03 4,43 23,27 278,70 -6,91 23,27 
7 1,5 13 2,42 58,53 4,43 7,01 -2289,1 128,8 7,01 
7 1,5 15 2,42 7,08 4,43 55,64 72,77 4,49 55,64 
7 1,5 17 2,42 3,09 4,43 10,62 -1964,3 112 10,62 
7 1,5 19 2,42 37,76 4,43 54,89 -908,24 57,47 54,89 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 70, 12 - 2020 63 
Kết quả tối ưu bằng thuật toán K-Nearest Neighbor tại khu đô thị Times City và Trường 
THPT Nguyễn Huệ có số mũ suy hao giống với số mũ suy hao khi xử lý bằng thuật toán Hồi quy 
tuyến tính, nhưng độ lệch chuẩn được tối ưu bằng thuật toán K-Nearest Neighbor thấp hơn. Điều 
này cho thấy thuật toán K-Nearest Neighbor cho kết quả tối ưu cuối cùng đối với mô hình CI tốt 
hơn thuật toán Hồi quy tuyến tính. Tuy nhiên, kết quả mô hình FI(NLOS) thì khác biệt rất nhiều 
do thuật toán K-Nearest Neighbor thực hiện lựa chọn k điểm dữ liệu liền kề gần nhất để tính giá 
trị của điểm mới làm cho các tham số của mô hình FI(NLOS) thay đổi liên tục và tạo ra sự khác 
biệt lớn và không chính xác. 
3.3. So sánh với kết quả của 3GPP và NYU Wireless 
3GPP đưa ra rất nhiều phép tính suy hao truyền sóng cho từng trường hợp và môi trường khác 
nhau, để so sánh kết quả thu được, tác giả chọn được hai phép tính của 3GPP phù hợp với mô 
hình mô phỏng khu vực khu đô thị Times City và trường THPT Nguyễn Huệ đó là [8]: 
Tần số 28 GHz: 
28 10(LOS)[dB]( ) 61,34 21log ( )(dB)( 4dB)GHzPL d d  (22) 
28 10(NLOS)[dB]( ) 61,34 31,9log ( )(dB)( 8,2dB)GHzPL d d  (23) 
Tần số 38 GHz: 
38 10(LOS)[dB]( ) 64 21log ( )(dB)( 4dB)GHzPL d d  (24) 
38 10(NLOS)[dB]( ) 64 31,9log ( )(dB)( 8,2dB)GHzPL d d  (25) 
Trong phép tính của 3GPP ở trên, số mũ suy hao trong môi trường đô thị lần lượt là 2,1 cho 
LOS và 3,19 cho NLOS. Kết quả của chúng tôi đạt được tại cả hai khu vực cho thấy khi tăng tần 
số máy phát làm cho số mũ suy hao cũng tăng theo và ở khu vực trường THPT Nguyễn Huệ do 
ảnh hưởng của cây cối và môi trường xung quanh nên số mũ suy hao cũng lớn hơn khu vực 
Times City. Tuy nhiên, các giá trị này chỉ dao động xung quanh hai giá trị số mũ suy hao phép 
tính của 3GPP chứ không cố định. Độ lệch chuẩn đạt được khi sử dụng thuật toán Hồi quy tuyến 
tính còn cao, nhưng khi sử dụng thuật toán KNN thì giá trị độ lệch chuẩn không sai lệch nhiều so 
với phép tính 3GPP ở trên. 
Ngoài ra, các kết quả về số mũ suy hao và độ lệch chuẩn của mô hình CI sau khi tối ưu cũng 
tương đương với kết quả của NYU Wireless (bảng 7) trong dự án đo ở thành phố New York, điều 
này chứng minh được tính hợp lý của các kết quả này. Đối với mô hình FI(NLOS), khi sử dụng 
thuật toán Hồi quy tuyến tính ở khu vực khu đô thị Times City, kết quả đạt được khá tương đồng 
với kết quả của NYU Wireless, mặc dù vậy, các kết quả mô phỏng còn lại ở khu vực trường THPT 
Nguyễn Huệ lại có nhiều khác biệt có thể do hạn chế công cụ mô phỏng và thiếu kinh nghiệm trong 
việc chọn vị trí máy thu tạo ra nhiều điểm ngoại vi nên mô hình thiếu chính xác. 
Bảng 7. Mô hình suy hao truyền sóng của NYU Wireless ở tần số 28 GHz [3]. 
f(GHz) 
Tx 
(m) 
Rx 
(m) 
LOS 
(Close-in) 
NLOS 
(Close-in) 
NLOS (floating-intercept) 
(30 m < d < 200 m) 
( n )  [dB] ( n ) 

[dB] 
 [dB]   [dB] 
28 7;17 1,5 2,1 3,6 3,4 9,7 79,2 2,6 9,6 
4. KẾT LUẬN 
Trong nghiên cứu này, tác giả đã ứng dụng hai thuật toán cơ bản của Học máy là Hồi quy 
tuyến tính và K-Nearest Neighbor để xây dựng mô hình suy hao truyền sóng ở tần số 28 GHz và 
38 GHz. Thuật toán Hồi quy tuyến tính dựa trên việc giảm khoảng cách (sai số) của các điểm dữ 
liệu cho đến đường thẳng tuyến tính cần tìm bằng cách tối ưu hàm mất mát bằng thuật toán 
Gradient Descent, trong khi đó, thuật toán K-Nearest Neighbor thì lại lựa chọn k điểm dữ liệu 
Kỹ thuật điều khiển & Điện tử 
 64 Đ. V. Linh, , V. V. Yêm, “Ứng dụng thuật toán học máy  truyền sóng dải sóng milimet.” 
gần nhất để huấn luyện tập dữ liệu và tìm ra giá trị k tối ưu cho mô hình. Để có kết quả khách 
quan về mô hình suy hao truyền sóng khi áp dụng hai thuật toán này, tác giả đã mô phỏng môi 
trường truyền sóng tại khu đô thị Times City và trường THPT Nguyễn Huệ cho cả hai tần số 28 
GHz và 38 GHz. Nhận thấy, tần số máy phát và địa hình khu vực mô phỏng đều ảnh hưởng đến 
số mũ suy hao của mô hình CI. Nhưng số mũ suy hao này vẫn hợp lý khi so sánh với phép tính 
của 3GPP và NYU Wireless. Thuật toán K-Nearest Neighbor cho kết quả tốt với độ lệch chuẩn 
của mô hình CI hơn thuật toán Hồi quy tuyến tính. Tuy nhiên, trong mô hình FI(NLOS) nếu xây 
dựng được mô hình có phạm vi mô phỏng tốt thì thuật toán Hồi quy tuyến tính cho kết quả tối ưu 
chính xác hơn. Do đó, việc kết hợp cả hai thuật toán này vào việc xây dựng mô hình suy hao 
truyền sóng dải sóng milimet sẽ giúp cải thiện kết quả tối ưu mô hình suy hao truyền sóng. 
TÀI LIỆU THAM KHẢO 
[1]. T. S. Rappaport, R. W. Heath, Jr., R. C. Daniels, and J. N. Murdock, “Millimeter Wave Wireless 
Communications,” Pearson/Prentice Hall, 2015. 
[2]. Z. Pi and F. Khan, “An introduction to millimeter-wave mobile broadband systems,” IEEE Commun. 
Mag., vol. 49, no. 6, Jun. 2011, pp. 101–107. 
[3]. G. R. MacCartney Jr., M. K. Samimi, and T. S. Rappaport, “Omnidirectional path loss models at 28 
GHz and 73 GHz in New York City,” Proc. IEEE Int. Symp. PIMRC, Sep. 2014. 
[4]. Östlin, E.; Zepernick, H.J.; Suzuki, H., “Macrocell path-loss prediction using artificial neural 
networks,” IEEE Trans. Veh. Technol. 2010, 59, 2735–2747. 
[5]. Isabona, J.; Srivastava, V.M., “Hybrid neural network approach for predicting signal propagation 
loss in urban microcells,” Proceedings of the 2016 IEEE Region 10 Humanitarian Technology 
Conference (R10-HTC), Agra, India, 21–23 December 2016, pp. 1-5. 
[6]. Cheikh A. L. DIAKHATE, “Propagation Channel Modeling at Centimeter–and–Millimeter–Wave 
Frequencies in 5G Urban Micro–cell Context”, Paris, France, 28 March 2019, pp. 56. 
[7]. Trevor Hastie, Robert Tibshirani, Jerome Friedman, “The Elements of Statistical Learning, Data 
Mining, Inference and Prediction”, Springer, 2009, pp. 14. 
[8]. “5G; Study on channel model for frequencies from 0.5 to 100 GHz” 07-2018 3GPP TR 38.901 
version 14.0.0 Release 15, pp. 24-27. 
ABSTRACT 
APPLYING MACHINE LEARNING ALGORITHMS 
FOR PATH LOSS PREDICTION OF MILLIMETER WAVES 
 In this paper, we develop and apply Linear Regression and K-Nearest Neighbor 
algorithm to predict the path loss models of millimeter waves. The experimental data is 
obtained by using Wireless Insite software, the experiments in both line-of-sight and non-
line-of-sight scenarios use a transmitter and receivers placed randomly at locations. The 
proposed method is applied to impove and adjust path loss models at 28 GHz and 38 GHz 
in Times City urban area and Nguyen Hue high school, Hanoi, Vietnam. The combination 
of these two algorithms to predict the path loss models of millimeter waves achieved the 
suitable results when compared with 3GPP and NYU Wireless path loss models, therefore 
improving the optimal results of path loss models. 
Keywords: K-Nearest Neighbor; Linear Regression; Gradient Descent; 5G; Millimeter waves; Path loss models. 
 Nhận bài ngày 04 tháng 9 năm 2020 
Hoàn thiện ngày 02 tháng 12 năm 2020 
Chấp nhận đăng ngày 14 tháng 12 năm 2020 
Địa chỉ: 1Học viện Kỹ thuật Mật mã – Ban Cơ yếu Chính phủ; 
 2Đại học Bách khoa Hà Nội. 
*
Email: yem.vuvan@hust.edu.vn.