Ứng dụng lý thuyết độ tin cậy trong tính toán ổn định đường hầm

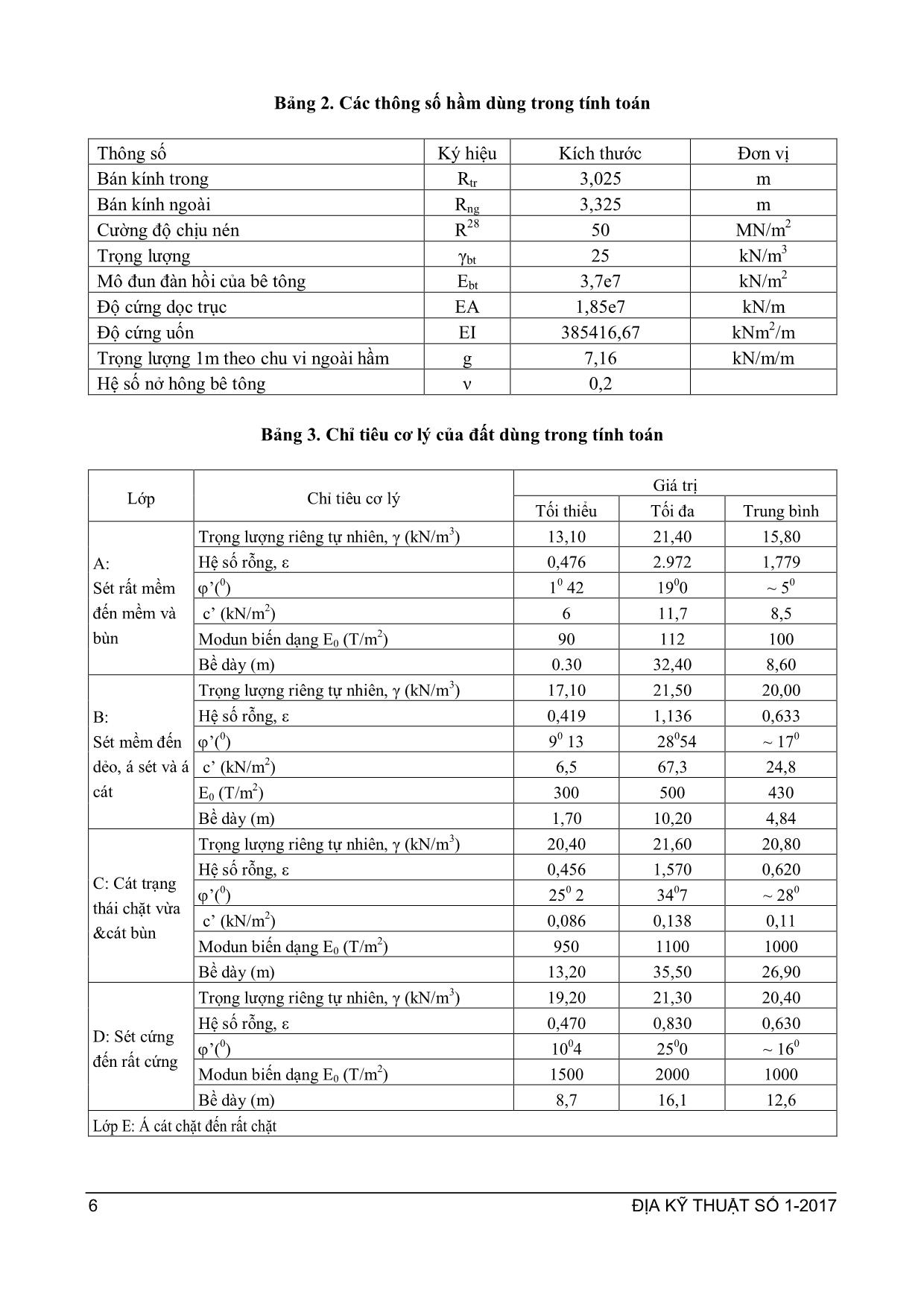
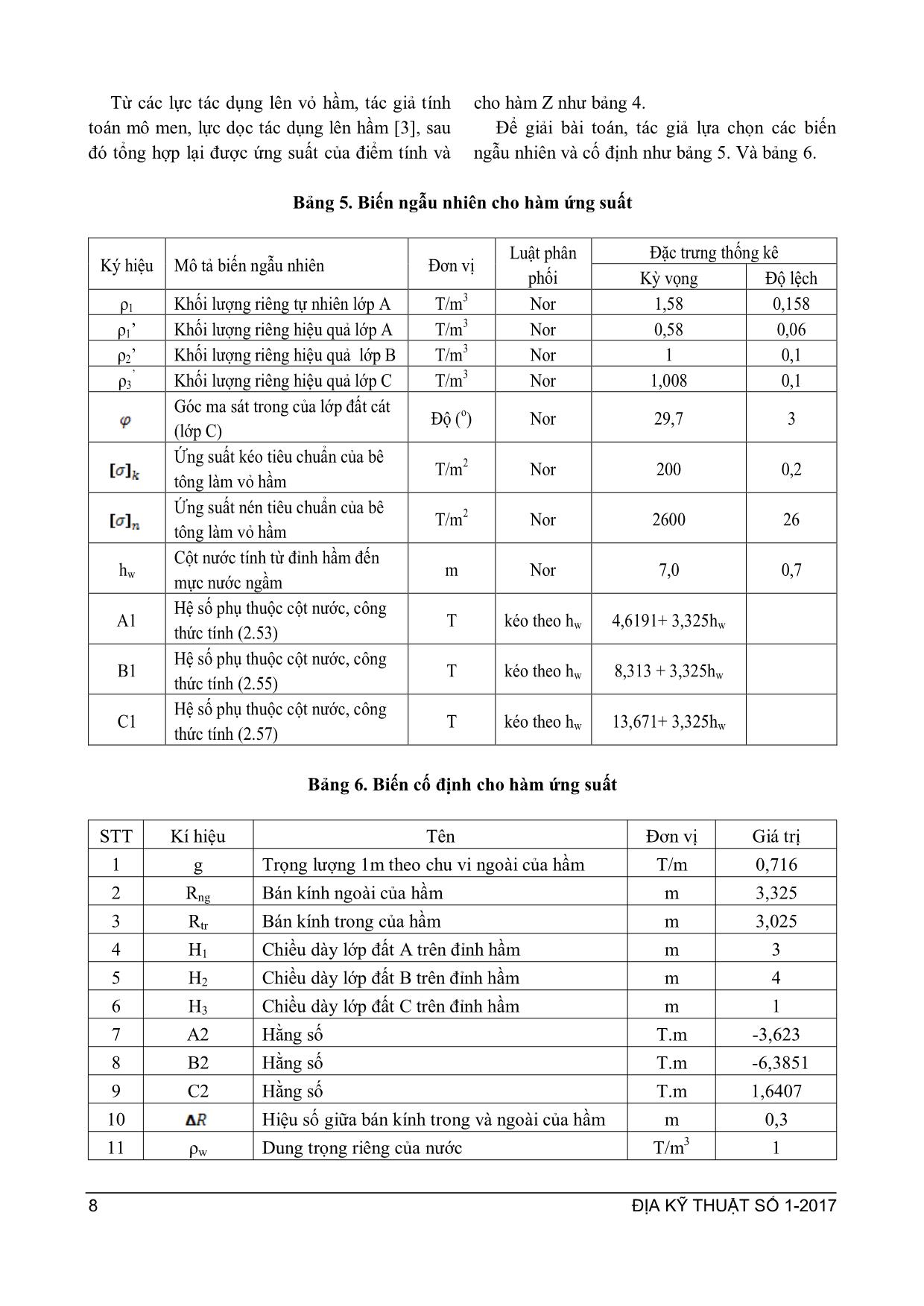
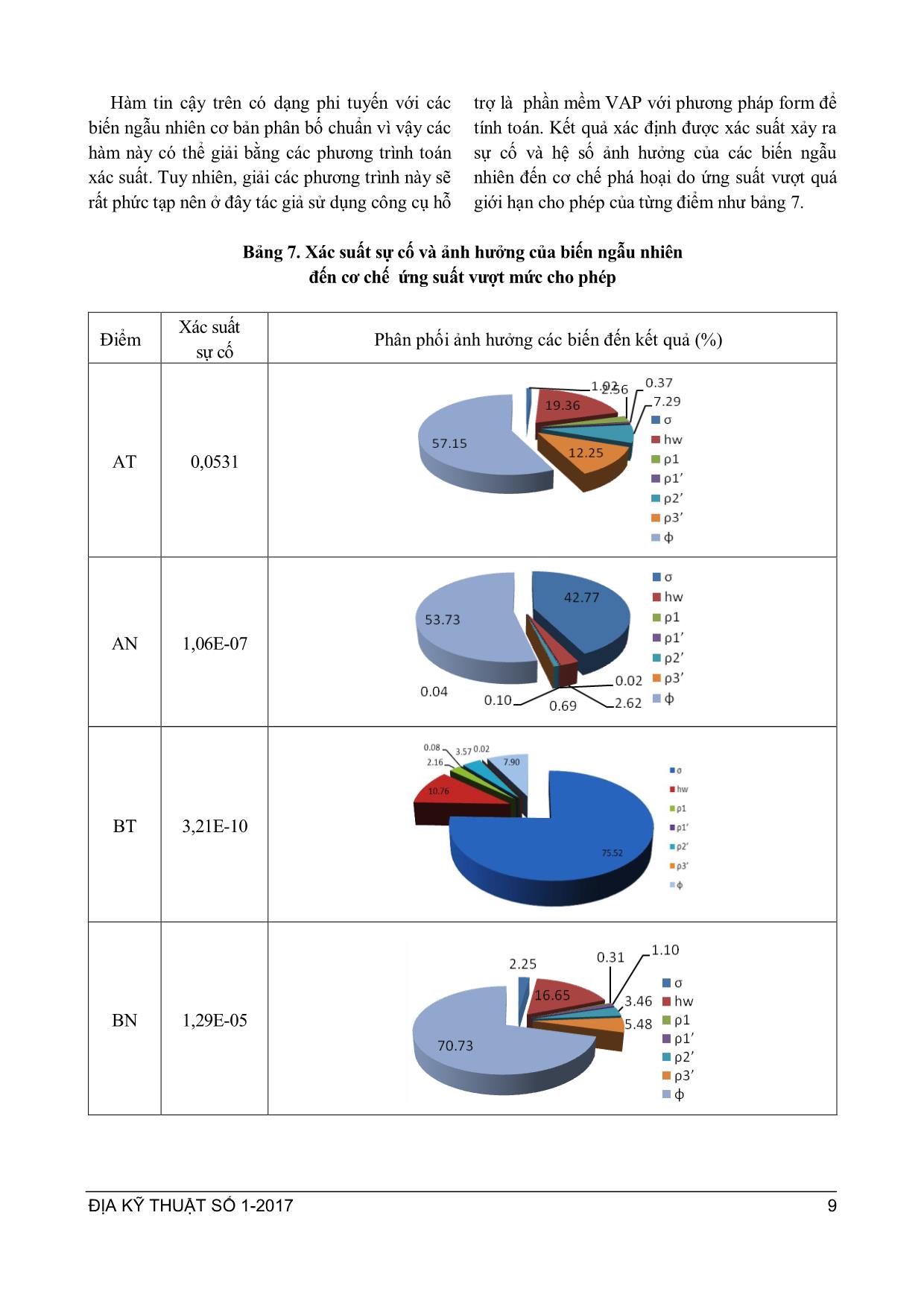
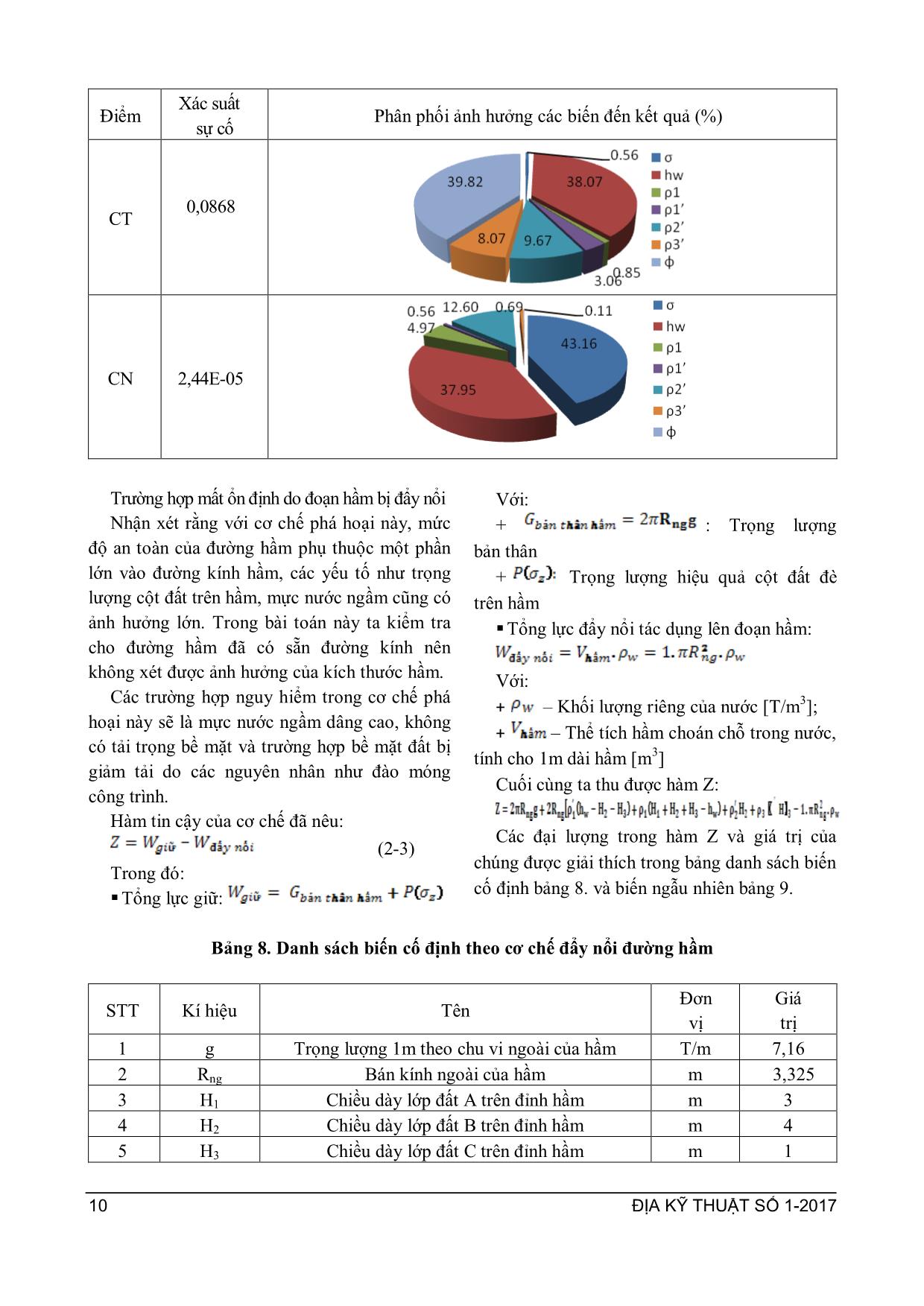
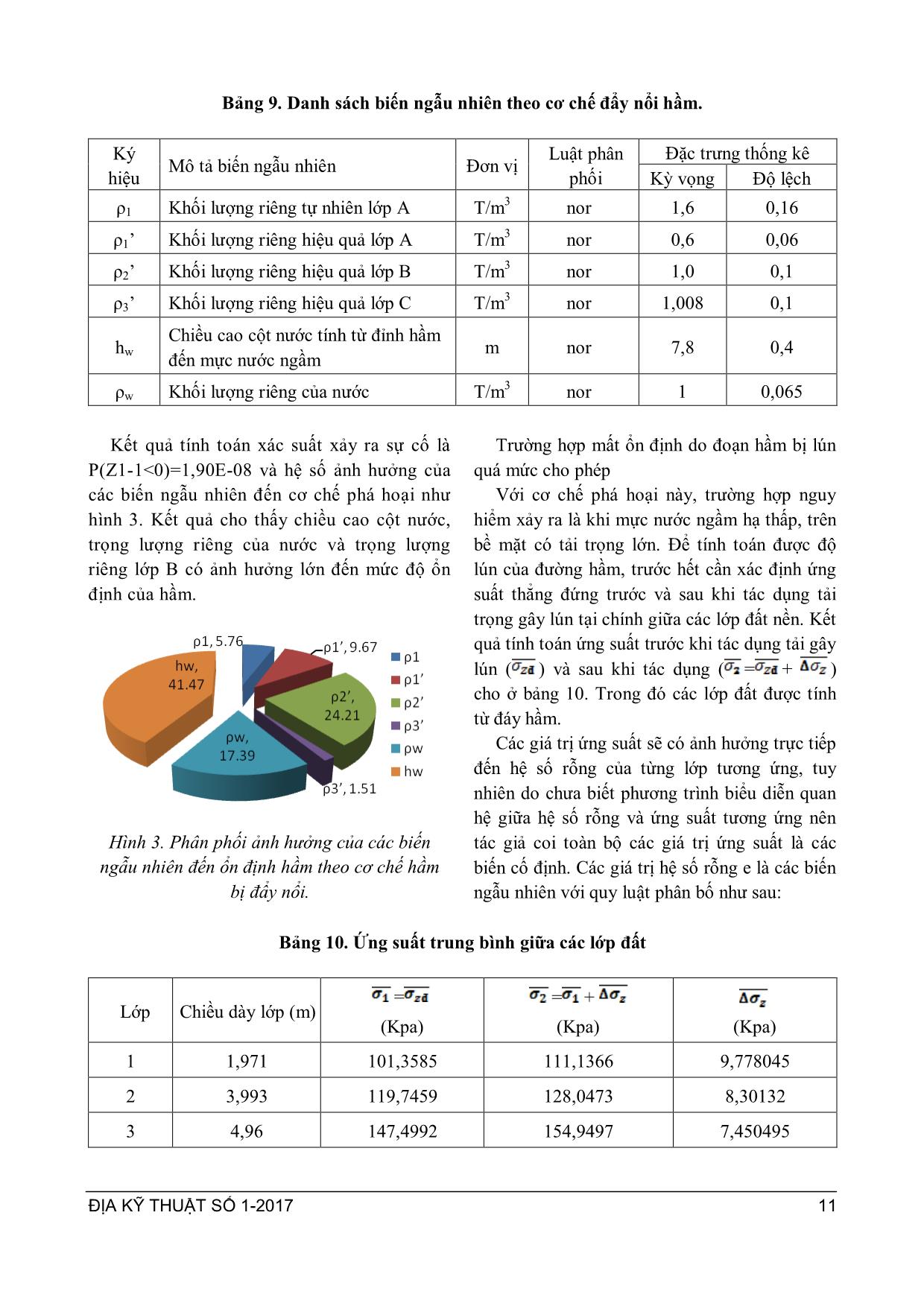
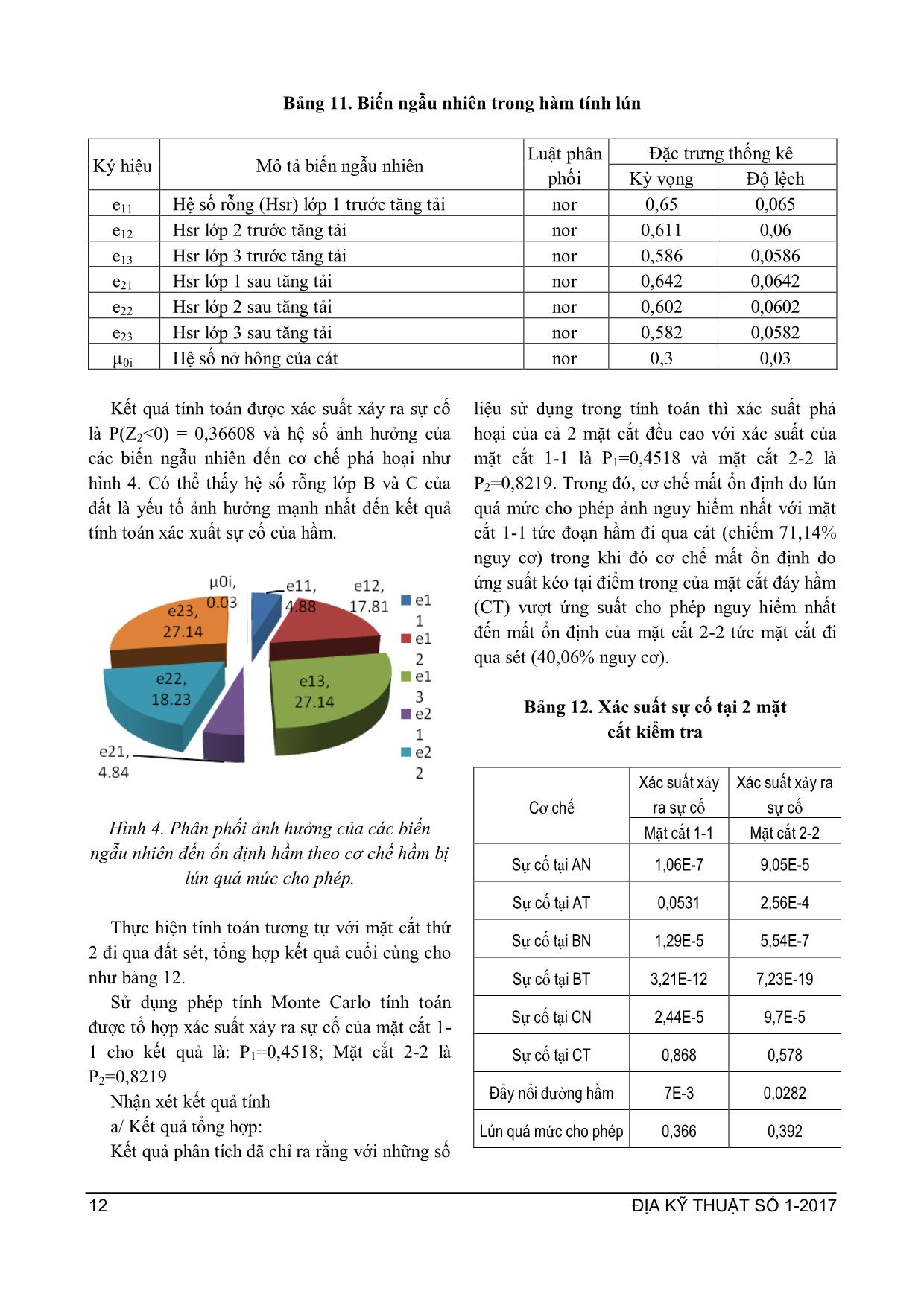
ĐỊA KỸ THUẬT SỐ 1-2017 3 
ỨNG DỤNG LÝ THUYẾT ĐỘ TIN CẬY TRONG 
TÍNH TOÁN ỔN ĐỊNH ĐƯỜNG HẦM 
HOÀNG THỊ LỤA* 
Application of reliability theory in analyzing tunnel stability 
Abstract: The purpose of this paper is to analysis the stability of tunnel by 
using reliability theory method. In this paper, the author first has developed 
a fault tree, then selected some common failure cases for detailed 
calculations. Three selected case were: 1. Tunnel was instable due to the 
stress exceeds the allowable value; 2. Tunnel was instable because of 
buoyant force; 3. Tunnel subsidance exceeds the allowable subsidence. In 
each case, the author has built reliability functions, selected random 
variables, studied the regularity of the distribution funtion of random 
variables and finally calculated incident probability. Consequently, incident 
probability of each case as well as general incident probability of tunnel 
was calculated. The effect of each variable to structure stability was also 
calculated. 
Keywords: Reliability theory, tunnel stability 
1. GIỚI THIỆU CHUNG * 
Việt Nam là một trong những quốc gia đông 
dân nhất thế giới với hơn 90 triệu ngƣời. Dân cƣ 
tập trung quá đông đúc trong các thành phố lớn 
đã khiến không gian sống, giao thông trở lên 
quá tải. Việc phát triển công trình ngầm là một 
biện pháp hợp lý và cần thiết để đáp ứng mật độ 
cao của dân số. 
Công trình ngầm thƣờng có đặc điểm là kéo 
dài hoặc mở rộng qua các vùng có tải trọng khác 
nhau, điều kiện địa chất khác nhau và các yếu tố 
này lại dao động, biến đổi theo thời gian. Tuy 
nhiên, khi tính toán thiết kế, các phƣơng pháp 
truyền thống thƣờng chỉ chọn một vài giá trị đặc 
trƣng của các thông số để tính toán mà chƣa xét 
đến sự dao động, biến đổi của các chỉ tiêu nói 
trên. Do đó, kết quả tính toán trong một số 
trƣờng hợp có thể chƣa phù hợp. 
Phƣơng pháp lý thuyết độ tin cậy (hay còn 
gọi là phƣơng pháp thiết kế ngẫu nhiên) là 
* Khoa Công trình - Đại học Thủy lợi 
 175 Tây Sơn - Đống Đa - Hà Nội 
 DĐ: 0912723376 
phƣơng pháp thiết kế dựa trên cơ sở toán xác 
suất thống kế để phân tích tƣơng tác giữa các 
biến ngẫu nhiên của tải trọng và sức chịu tải 
trong các cơ chế phá hoại theo giới hạn làm việc 
của công trình. Trong thiết kế ngẫu nhiên, tất cả 
các cơ chế phá hỏng đƣợc mô tả bởi mô hình 
toán hoặc mô hình mô phỏng tƣơng ứng. Tính 
toán xác suất phá hỏng của một bộ phận kết cấu 
hoặc của công trình đƣợc dựa trên hàm độ tin 
cậy của từng cơ chế phá hỏng. 
Hàm độ tin cậy này đƣợc thiết lập dựa vào 
trạng thái giới hạn tƣơng ứng với cơ chế phá 
hỏng tƣơng ứng và là hàm của nhiều biến và 
tham số ngẫu nhiên. Do đó kết quả tính toán từ 
phƣơng pháp độ tin cậy không những cho xác 
suất phá hỏng của từng cơ chế đơn lẻ mà còn 
cho biết mức độ ảnh hƣởng của từng biến ngẫu 
nhiên và tổng hợp cho ta xác suất cuối cùng của 
cả hệ thống đang xem xét. Trên thế giới, thiết kế 
theo xác suất an toàn cho phép đã đƣợc nghiên 
cứu và đƣa vào ứng dụng từ lâu. Ở Việt Nam, lý 
thuyết độ tin cậy cũng đã đƣợc đƣa vào chƣơng 
trình giảng dạy của một số trƣờng đại học và 
 ĐỊA KỸ THUẬT SỐ 1-2017 4 
đƣợc nghiên cứu trong lĩnh vực xây dựng công 
trình thủy. Bài báo này sẽ đề cập đến việc ứng 
dụng lý thuyết độ tin cậy trong phân tích ổn 
định của công trình ngầm. 
2. CƠ SỞ LÝ THUYẾT CỦA PHƢƠNG 
PHÁP 
2.1. Tóm tắt cơ sở lý thuyết 
Để xem xét đƣợc mức độ an toàn của một 
thành phần , ngƣời ta thành lập một hàm tin cậy 
có dạng tổng quát nhƣ sau: 
Z = R-S (2.1) 
Với: + R – Độ bền hay khả năng kháng hƣ 
hỏng; 
 + S – Tải trọng hay khả năng gây hƣ hỏng. 
Theo đó, Z<0 đƣợc coi là có hƣ hỏng xảy ra 
và hƣ hỏng không xảy ra nếu Z >0, còn khi Z=0 
thì ở ranh giới giữa vùng an toàn và không an 
toàn. 
Xác suất phá hỏng của từng cơ chế đƣợc xác 
định bởi xác suất xảy ra Z<0: Pf = P(Z≤0) = 
P(S≥R) 
Độ tin cậy đƣợc xác định là : P(Z>0) = 1-Pf 
Hình 1. Hàm tin cậy trong mặt phẳng RS [2] 
Hàm xác suất có thể đƣợc giải theo các mức 
độ tiếp cận nhƣ sau: 
- Tiếp cận mức độ xác suất cấp độ 0, mức độ 
này là phƣơng pháp thiết kế truyền thống, sử 
dụng hệ số an toàn để đánh giá. 
- Tiếp cận mức độ xác suất cấp độ I, mức độ 
này là thiết kế bán xác suất, sử dụng nhiều hệ 
số an toàn để đánh giá ổn định (phƣơng pháp 
trạng thái giới hạn). 
- Tiếp cận xác suất cấp độ II và cấp độ III, 
đây là phƣơng pháp tiếp cận ngẫu nhiên. Trong 
đó, cấp độ II sử dụng các phƣơng pháp gần 
đúng để biến đổi quy luật phân bố của các tải 
trọng và sức chịu tải về các hàm phân bố 
chuẩn, sử dụng các phƣơng pháp xác suất gần 
đúng trong tính toán. Đối với mức độ III, các 
hàm phân bố của các biến đƣợc giữ nguyên 
quy luật phân bố và trong tính toán không sử 
dụng các phƣơng pháp gần đúng, ngẫu nhiên 
hoàn toàn. Bài báo này sẽ trình bày bài toán ở 
cấp độ II(*). [2] 
2.2. Các cơ chế phá hoại đƣờng hầm 
Có nhiều nguyên nhân có thể dẫn đến mất ổn 
định đƣờng hầm. Các giai đoạn khác n ...  lún cố kết ổn định tính toán [m]; 
Độ lún cố kết ổn định đối với hầm tác giả coi 
là bài toán tính lún theo hai hƣớng (coi nhƣ 
không biến dạng dọc trục hầm). Và độ lún trong 
trƣờng hợp này do tải trọng bề mặt gây ra, gây 
lún nền hầm kéo theo lún đốt hầm. Công thức 
tính lún cho lớp i (2-5) và độ lún tổng của nền 
hầm (2-6) 
Si= 
11 12
21
2
00
0
121
18.0
e
hee izi
n
i ii
i




 (2-5) 
Sc = 
n
1i
iS (2-6) 
* Trong đó: 
+ 1 và 2 lần lƣợt là ứng suất trung bình 
thẳng đứng tại lớp i ứng với giai đoạn trƣớc và 
sau khi tác dụng ứng suất gây lún. 
+ zi: Ứng suất thẳng đứng trung bình gây 
lún lớp thứ i 
+ : Hệ số nở hông lớp thứ i 
+ hi: Chiều dày lớp i; 
+ e1i và e2i lần lƣợt là hệ số rỗng lớp i ứng 
với giai đoạn trƣớc và sau khi tác dụng ứng suất 
gây lún. 
3. ÁP DỤNG TÍNH TOÁN 
3.1. Giới thiệu công trình nghiên cứu 
Trong phần này tác giả sẽ áp dụng tính toán 
với các số liệu đã thu thập đƣợc từ dự án hầm 
giao thông Metro II, thành phố Hồ Chí Minh. 
Đƣờng hầm có dạng khuyên tròn, các đốt 
hầm bằng bê tông cốt thép đƣợc chế tạo sẵn, thi 
công bằng máy đào ngầm, có các thông số nhƣ 
bảng 2. 
Đƣờng hầm nằm ở độ sâu trung bình khoảng 
12m dƣới mặt đất tự nhiên, chỉ tiêu cơ lý của 
các lớp đất sử dụng trong tính toán từ mặt đất tự 
nhiên xuống lần lƣợt nhƣ bảng 3.[4] 
 ĐỊA KỸ THUẬT SỐ 1-2017 6 
Bảng 2. Các thông số hầm dùng trong tính toán 
Thông số Ký hiệu Kích thƣớc Đơn vị 
Bán kính trong Rtr 3,025 m 
Bán kính ngoài Rng 3,325 m 
Cƣờng độ chịu nén R28 50 MN/m2 
Trọng lƣợng γbt 25 kN/m
3
Mô đun đàn hồi của bê tông Ebt 3,7e7 kN/m
2
Độ cứng dọc trục EA 1,85e7 kN/m 
Độ cứng uốn EI 385416,67 kNm2/m 
Trọng lƣợng 1m theo chu vi ngoài hầm g 7,16 kN/m/m 
Hệ số nở hông bê tông ν 0,2 
Bảng 3. Chỉ tiêu cơ lý của đất dùng trong tính toán 
Lớp Chỉ tiêu cơ lý 
Giá trị 
Tối thiểu Tối đa Trung bình 
A: 
Sét rất mềm 
đến mềm và 
bùn 
Trọng lƣợng riêng tự nhiên, γ (kN/m3) 13,10 21,40 15,80 
Hệ số rỗng, ε 0,476 2.972 1,779 
 ’(0) 10 42 1900 ~ 50 
 c’ (kN/m2) 6 11,7 8,5 
Modun biến dạng E0 (T/m
2
) 90 112 100 
Bề dày (m) 0.30 32,40 8,60 
B: 
Sét mềm đến 
dẻo, á sét và á 
cát 
Trọng lƣợng riêng tự nhiên, γ (kN/m3) 17,10 21,50 20,00 
Hệ số rỗng, ε 0,419 1,136 0,633 
 ’(0) 90 13 28054 ~ 170 
 c’ (kN/m2) 6,5 67,3 24,8 
E0 (T/m
2
) 300 500 430 
Bề dày (m) 1,70 10,20 4,84 
C: Cát trạng 
thái chặt vừa 
&cát bùn 
Trọng lƣợng riêng tự nhiên, γ (kN/m3) 20,40 21,60 20,80 
Hệ số rỗng, ε 0,456 1,570 0,620 
 ’(0) 250 2 3407 ~ 280 
 c’ (kN/m2) 0,086 0,138 0,11 
Modun biến dạng E0 (T/m
2
) 950 1100 1000 
Bề dày (m) 13,20 35,50 26,90 
D: Sét cứng 
đến rất cứng 
Trọng lƣợng riêng tự nhiên, γ (kN/m3) 19,20 21,30 20,40 
Hệ số rỗng, ε 0,470 0,830 0,630 
 ’(0) 1004 2500 ~ 160 
Modun biến dạng E0 (T/m
2
) 1500 2000 1000 
Bề dày (m) 8,7 16,1 12,6 
Lớp E: Á cát chặt đến rất chặt 
ĐỊA KỸ THUẬT SỐ 1-2017 7 
3.2. Xây dựng sơ đồ lực tác dụng lên vỏ hầm 
Với những đặc điểm về địa chất và vị trí hầm 
trong đất, tác giả xây dựng sơ đồ lực tác dụng 
lên vỏ hầm theo mô hình cân bằng giới hạn cho 
hầm đặt sâu, không xét đến sự hình thành vòm 
áp lực phía trên đỉnh hầm do đất phía trên hầm 
là đất yếu bão hòa[4]. Các áp lực tác dụng lên 
hầm bao gồm áp lực thẳng đứng, nằm ngang của 
đất và tải trọng bề mặt truyền xuống, áp lực của 
nƣớc theo phƣơng vuông góc với bề mặt vỏ hầm 
và trọng lƣợng bản thân của hầm. Sơ đồ lực tác 
dụng lên vỏ hầm đƣợc thể hiện nhƣ hình 2. 
Hình 2. Sơ đồ lực tác dụng lên hầm 
3.2. Tính toán ổn định hầm 
Trong phần này tác giả sẽ tính toán cho hai mặt 
cắt điển hình, mặt cắt 1-1 với hầm đi qua lớp sét B 
và mặt cắt 2-2 với hầm đi qua lớp cát C 
Trƣờng hợp mất ổn định do ứng suất vƣợt 
mức cho phép 
Đối với cơ chế phá hoại này tác giả lựa chọn 
tính toán tại 6 điểm nguy hiểm nhƣ hình 3. 
Hình 3. Các điểm tính toán ứng suất 
Trong đó các điểm AT, BN, CT chịu kéo, ba 
điểm còn lại AN, BT, CN chịu nén. 
Từ hàm tính: 
 (2-2) 
Bảng 4. Hàm tin cậy về ứng suất của các điểm tính 
Điểm 
tính 
Hàm tin cậy Z 
A 
B 
C 
 ĐỊA KỸ THUẬT SỐ 1-2017 8 
Từ các lực tác dụng lên vỏ hầm, tác giả tính 
toán mô men, lực dọc tác dụng lên hầm [3], sau 
đó tổng hợp lại đƣợc ứng suất của điểm tính và 
cho hàm Z nhƣ bảng 4. 
Để giải bài toán, tác giả lựa chọn các biến 
ngẫu nhiên và cố định nhƣ bảng 5. Và bảng 6. 
Bảng 5. Biến ngẫu nhiên cho hàm ứng suất 
Ký hiệu Mô tả biến ngẫu nhiên Đơn vị 
Luật phân 
phối 
Đặc trƣng thống kê 
Kỳ vọng Độ lệch 
ρ1 Khối lƣợng riêng tự nhiên lớp A T/m
3
 Nor 1,58 0,158 
ρ1’ Khối lƣợng riêng hiệu quả lớp A T/m
3
 Nor 0,58 0,06 
ρ2’ Khối lƣợng riêng hiệu quả lớp B T/m
3
 Nor 1 0,1 
ρ3
’ Khối lƣợng riêng hiệu quả lớp C T/m3 Nor 1,008 0,1 
Góc ma sát trong của lớp đất cát 
(lớp C) 
Độ (o) Nor 29,7 3 
Ứng suất kéo tiêu chuẩn của bê 
tông làm vỏ hầm 
T/m
2
 Nor 200 0,2 
Ứng suất nén tiêu chuẩn của bê 
tông làm vỏ hầm 
T/m
2
 Nor 2600 26 
hw 
Cột nƣớc tính từ đỉnh hầm đến 
mực nƣớc ngầm 
m Nor 7,0 0,7 
A1 
Hệ số phụ thuộc cột nƣớc, công 
thức tính (2.53) 
T kéo theo hw 4,6191+ 3,325hw 
B1 
Hệ số phụ thuộc cột nƣớc, công 
thức tính (2.55) 
T kéo theo hw 8,313 + 3,325hw 
C1 
Hệ số phụ thuộc cột nƣớc, công 
thức tính (2.57) 
T kéo theo hw 13,671+ 3,325hw 
Bảng 6. Biến cố định cho hàm ứng suất 
STT Kí hiệu Tên Đơn vị Giá trị 
1 g Trọng lƣợng 1m theo chu vi ngoài của hầm T/m 0,716 
2 Rng Bán kính ngoài của hầm m 3,325 
3 Rtr Bán kính trong của hầm m 3,025 
4 H1 Chiều dày lớp đất A trên đỉnh hầm m 3 
5 H2 Chiều dày lớp đất B trên đỉnh hầm m 4 
6 H3 Chiều dày lớp đất C trên đỉnh hầm m 1 
7 A2 Hằng số T.m -3,623 
8 B2 Hằng số T.m -6,3851 
9 C2 Hằng số T.m 1,6407 
10 Hiệu số giữa bán kính trong và ngoài của hầm m 0,3 
11 ρw Dung trọng riêng của nƣớc T/m
3
 1 
ĐỊA KỸ THUẬT SỐ 1-2017 9 
Hàm tin cậy trên có dạng phi tuyến với các 
biến ngẫu nhiên cơ bản phân bố chuẩn vì vậy các 
hàm này có thể giải bằng các phƣơng trình toán 
xác suất. Tuy nhiên, giải các phƣơng trình này sẽ 
rất phức tạp nên ở đây tác giả sử dụng công cụ hỗ 
trợ là phần mềm VAP với phƣơng pháp form để 
tính toán. Kết quả xác định đƣợc xác suất xảy ra 
sự cố và hệ số ảnh hƣởng của các biến ngẫu 
nhiên đến cơ chế phá hoại do ứng suất vƣợt quá 
giới hạn cho phép của từng điểm nhƣ bảng 7. 
Bảng 7. Xác suất sự cố và ảnh hƣởng của biến ngẫu nhiên 
đến cơ chế ứng suất vƣợt mức cho phép 
Điểm 
Xác suất 
sự cố 
Phân phối ảnh hƣởng các biến đến kết quả (%) 
AT 0,0531 
AN 1,06E-07 
BT 3,21E-10 
BN 1,29E-05 
 ĐỊA KỸ THUẬT SỐ 1-2017 10 
Điểm 
Xác suất 
sự cố 
Phân phối ảnh hƣởng các biến đến kết quả (%) 
CT 
0,0868 
CN 2,44E-05 
Trƣờng hợp mất ổn định do đoạn hầm bị đẩy nổi 
Nhận xét rằng với cơ chế phá hoại này, mức 
độ an toàn của đƣờng hầm phụ thuộc một phần 
lớn vào đƣờng kính hầm, các yếu tố nhƣ trọng 
lƣợng cột đất trên hầm, mực nƣớc ngầm cũng có 
ảnh hƣởng lớn. Trong bài toán này ta kiểm tra 
cho đƣờng hầm đã có sẵn đƣờng kính nên 
không xét đƣợc ảnh hƣởng của kích thƣớc hầm. 
Các trƣờng hợp nguy hiểm trong cơ chế phá 
hoại này sẽ là mực nƣớc ngầm dâng cao, không 
có tải trọng bề mặt và trƣờng hợp bề mặt đất bị 
giảm tải do các nguyên nhân nhƣ đào móng 
công trình. 
Hàm tin cậy của cơ chế đã nêu: 
 (2-3) 
Trong đó: 
 Tổng lực giữ: 
Với: 
+ : Trọng lƣợng 
bản thân 
+ Trọng lƣợng hiệu quả cột đất đè 
trên hầm 
 Tổng lực đẩy nổi tác dụng lên đoạn hầm: 
Với: 
+ – Khối lƣợng riêng của nƣớc [T/m3]; 
+ – Thể tích hầm choán chỗ trong nƣớc, 
tính cho 1m dài hầm [m3] 
Cuối cùng ta thu đƣợc hàm Z: 
Các đại lƣợng trong hàm Z và giá trị của 
chúng đƣợc giải thích trong bảng danh sách biến 
cố định bảng 8. và biến ngẫu nhiên bảng 9. 
Bảng 8. Danh sách biến cố định theo cơ chế đẩy nổi đƣờng hầm 
STT Kí hiệu Tên 
Đơn 
vị 
Giá 
trị 
1 g Trọng lƣợng 1m theo chu vi ngoài của hầm T/m 7,16 
2 Rng Bán kính ngoài của hầm m 3,325 
3 H1 Chiều dày lớp đất A trên đỉnh hầm m 3 
4 H2 Chiều dày lớp đất B trên đỉnh hầm m 4 
5 H3 Chiều dày lớp đất C trên đỉnh hầm m 1 
ĐỊA KỸ THUẬT SỐ 1-2017 11 
Bảng 9. Danh sách biến ngẫu nhiên theo cơ chế đẩy nổi hầm. 
Ký 
hiệu 
Mô tả biến ngẫu nhiên Đơn vị 
Luật phân 
phối 
Đặc trƣng thống kê 
Kỳ vọng Độ lệch 
ρ1 Khối lƣợng riêng tự nhiên lớp A T/m
3
 nor 1,6 0,16 
ρ1’ Khối lƣợng riêng hiệu quả lớp A T/m
3
 nor 0,6 0,06 
ρ2’ Khối lƣợng riêng hiệu quả lớp B T/m
3
 nor 1,0 0,1 
ρ3’ Khối lƣợng riêng hiệu quả lớp C T/m
3
 nor 1,008 0,1 
hw 
Chiều cao cột nƣớc tính từ đỉnh hầm 
đến mực nƣớc ngầm 
m nor 7,8 0,4 
ρw Khối lƣợng riêng của nƣớc T/m
3
 nor 1 0,065 
Kết quả tính toán xác suất xảy ra sự cố là 
P(Z1-1<0)=1,90E-08 và hệ số ảnh hƣởng của 
các biến ngẫu nhiên đến cơ chế phá hoại nhƣ 
hình 3. Kết quả cho thấy chiều cao cột nƣớc, 
trọng lƣợng riêng của nƣớc và trọng lƣợng 
riêng lớp B có ảnh hƣởng lớn đến mức độ ổn 
định của hầm. 
Hình 3. Phân phối ảnh hưởng của các biến 
ngẫu nhiên đến ổn định hầm theo cơ chế hầm 
bị đẩy nổi. 
Trƣờng hợp mất ổn định do đoạn hầm bị lún 
quá mức cho phép 
Với cơ chế phá hoại này, trƣờng hợp nguy 
hiểm xảy ra là khi mực nƣớc ngầm hạ thấp, trên 
bề mặt có tải trọng lớn. Để tính toán đƣợc độ 
lún của đƣờng hầm, trƣớc hết cần xác định ứng 
suất thẳng đứng trƣớc và sau khi tác dụng tải 
trọng gây lún tại chính giữa các lớp đất nền. Kết 
quả tính toán ứng suất trƣớc khi tác dụng tải gây 
lún ( ) và sau khi tác dụng ( = + ) 
cho ở bảng 10. Trong đó các lớp đất đƣợc tính 
từ đáy hầm. 
Các giá trị ứng suất sẽ có ảnh hƣởng trực tiếp 
đến hệ số rỗng của từng lớp tƣơng ứng, tuy 
nhiên do chƣa biết phƣơng trình biểu diễn quan 
hệ giữa hệ số rỗng và ứng suất tƣơng ứng nên 
tác giả coi toàn bộ các giá trị ứng suất là các 
biến cố định. Các giá trị hệ số rỗng e là các biến 
ngẫu nhiên với quy luật phân bố nhƣ sau: 
Bảng 10. Ứng suất trung bình giữa các lớp đất 
Lớp Chiều dày lớp (m) 
= 
(Kpa) 
= + 
(Kpa) 
(Kpa) 
1 1,971 101,3585 111,1366 9,778045 
2 3,993 119,7459 128,0473 8,30132 
3 4,96 147,4992 154,9497 7,450495 
 ĐỊA KỸ THUẬT SỐ 1-2017 12 
Bảng 11. Biến ngẫu nhiên trong hàm tính lún 
Ký hiệu Mô tả biến ngẫu nhiên 
Luật phân 
phối 
Đặc trƣng thống kê 
Kỳ vọng Độ lệch 
e11 Hệ số rỗng (Hsr) lớp 1 trƣớc tăng tải nor 0,65 0,065 
e12 Hsr lớp 2 trƣớc tăng tải nor 0,611 0,06 
e13 Hsr lớp 3 trƣớc tăng tải nor 0,586 0,0586 
e21 Hsr lớp 1 sau tăng tải nor 0,642 0,0642 
e22 Hsr lớp 2 sau tăng tải nor 0,602 0,0602 
e23 Hsr lớp 3 sau tăng tải nor 0,582 0,0582 
µ0i Hệ số nở hông của cát nor 0,3 0,03 
Kết quả tính toán đƣợc xác suất xảy ra sự cố 
là P(Z2<0) = 0,36608 và hệ số ảnh hƣởng của 
các biến ngẫu nhiên đến cơ chế phá hoại nhƣ 
hình 4. Có thể thấy hệ số rỗng lớp B và C của 
đất là yếu tố ảnh hƣởng mạnh nhất đến kết quả 
tính toán xác xuất sự cố của hầm. 
Hình 4. Phân phối ảnh hưởng của các biến 
ngẫu nhiên đến ổn định hầm theo cơ chế hầm bị 
lún quá mức cho phép. 
Thực hiện tính toán tƣơng tự với mặt cắt thứ 
2 đi qua đất sét, tổng hợp kết quả cuối cùng cho 
nhƣ bảng 12. 
Sử dụng phép tính Monte Carlo tính toán 
đƣợc tổ hợp xác suất xảy ra sự cố của mặt cắt 1-
1 cho kết quả là: P1=0,4518; Mặt cắt 2-2 là 
P2=0,8219 
Nhận xét kết quả tính 
a/ Kết quả tổng hợp: 
Kết quả phân tích đã chỉ ra rằng với những số 
liệu sử dụng trong tính toán thì xác suất phá 
hoại của cả 2 mặt cắt đều cao với xác suất của 
mặt cắt 1-1 là P1=0,4518 và mặt cắt 2-2 là 
P2=0,8219. Trong đó, cơ chế mất ổn định do lún 
quá mức cho phép ảnh nguy hiểm nhất với mặt 
cắt 1-1 tức đoạn hầm đi qua cát (chiếm 71,14% 
nguy cơ) trong khi đó cơ chế mất ổn định do 
ứng suất kéo tại điểm trong của mặt cắt đáy hầm 
(CT) vƣợt ứng suất cho phép nguy hiểm nhất 
đến mất ổn định của mặt cắt 2-2 tức mặt cắt đi 
qua sét (40,06% nguy cơ). 
Bảng 12. Xác suất sự cố tại 2 mặt 
cắt kiểm tra 
Cơ chế 
Xác suất xảy 
ra sự cố 
Xác suất xảy ra 
sự cố 
Mặt cắt 1-1 Mặt cắt 2-2 
Sự cố tại AN 1,06E-7 9,05E-5 
Sự cố tại AT 0,0531 2,56E-4 
Sự cố tại BN 1,29E-5 5,54E-7 
Sự cố tại BT 3,21E-12 7,23E-19 
Sự cố tại CN 2,44E-5 9,7E-5 
Sự cố tại CT 0,868 0,578 
Đẩy nổi đƣờng hầm 7E-3 0,0282 
Lún quá mức cho phép 0,366 0,392 
ĐỊA KỸ THUẬT SỐ 1-2017 13 
b/ Kết quả thành phần 
+ Đối với cơ chế ứng suất vƣợt mức 
cho phép: 
Trong các điểm tác giả thực hiện kiểm tra 
thì hầu hết xác suất sự cố P(Z<0) đều nhỏ, các 
điểm chịu ứng suất kéo có xác suất sự cố cao 
hơn các điểm chịu nén. Điểm có nguy cơ bị 
phá hoại lớn nhất là điểm CT (điểm ở mặt 
trong đáy hầm). 
Trong phạm vi biến ngẫu nhiên mà tác giả 
đã lựa chọn thì: Các điểm hai bên hầm (BN, 
BT) bị ảnh hƣởng mạnh nhất bởi cƣờng độ 
chống cắt của đất xung quanh, trong khi đó 
các điểm nằm ở đỉnh và đáy (CN, CT) thì lại 
chịu ảnh hƣởng lớn bởi các trọng lƣợng riêng 
của đất và đặc biệt là cột nƣớc tác dụng lên vỏ 
hầm chiếm một tỷ lệ cao trong biểu đồ phân 
phối các hệ số ảnh hƣởng. 
+ Đối với cơ chế hầm bị đẩy nổi: các biến 
trọng lƣợng riêng của nƣớc, chiều cao cột nƣớc 
và trọng lƣợng riêng của đất trên hầm đều là 
những yếu tố ảnh hƣởng mạnh đến xác suất đẩy 
nổi đoạn hầm. Tuy nhiên với độ sâu chôn hầm 
và các chỉ tiêu tính toán ở đây thì xác suất sự cố 
này rất thấp, chỉ khoảng 0,0282 (2,82%). 
+ Đối với cơ chế đốt hầm lún quá mức cho 
phép: cả hai mặt cắt đều cho xác suất nền hầm 
bị lún quá mức cho phép khá cao và hệ số rỗng 
của các lớp đất là yếu tố ảnh hƣởng mạnh đến 
mức độ lún nền hầm. Tuy nhiên kết quả này chỉ 
là tính toán ứng với trạng thái hoàn toàn tự 
nhiên của đất nền. 
4. KẾT LUẬN 
Trên cơ sở tiếp cận tính toán theo cấp độ II, 
tính toán dựa vào phần mềm VAP và tổ hợp xác 
suất theo thuật toán Monte Carlo, các kết luận 
chính có thể rút ra là: 
(1) Tính đƣợc xác suất sự cố của từng cơ 
chế, tổng hợp đƣợc xác suất của các cơ chế vào 
xác suất sự cố toàn mặt cắt hầm. 
(2) Tính toán đƣợc mức độ ảnh hƣởng của 
từng biến ngẫu nhiên đến kết quả tính toán, từ 
đó cho thấy sự dao động của biến nào sẽ tác 
động mạnh đến xác suất sự cố. 
(3) Kết quả tính toán khá hợp lý khi so sánh 
với kết quả tính truyền thống (nhƣ điểm có ứng 
suất nguy hiểm nhất, nguy cơ mất ổn định cao 
do lún quá mức cho phép) 
TÀI LIỆU THAM KHẢO 
1. Bộ môn Địa Kỹ Thuật, 2011; Bài giảng Cơ 
học đất, Khoa Công Trình, Đại học Thủy lợi. 
2. Mai Văn Công, 2006; Thiết kế công trình 
theo lý thuyết ngẫu nhiên và phân tích độ tin 
cậy; Bài giảng Khoa Kỹ Thuật Biển, Đại học 
Thủy lợi. 
3. Trần Thanh Giám-Tạ Tiến Đạt, 2011; 
Tính toán thiết kế công trình ngầm, nhà xuất 
bản Xây Dựng, Hà Nội 
4. Sở kế hoạch và đầu tƣ thành phố Hồ Chí 
Minh, 2011; Báo cáo tóm tắt nghiên cứu khả 
thi tuyến tàu điện ngầm số 2 thành phố Hồ 
Chí Minh. 
5. Civil Engineering and Development 
Department, Geotechnical Engineering office, 
2012; Catalogue of Notable tunnel Failure Case 
6. www.sciencedirect.com 
7. Taudienngam.net
Người phản biện: GS. NGUYỄN CÔNG MẪN