Tối ưu cấu trúc quỹ đạo hệ thống vệ tinh giám sát liên tục khoảng không gian vũ trụ gần trái đất
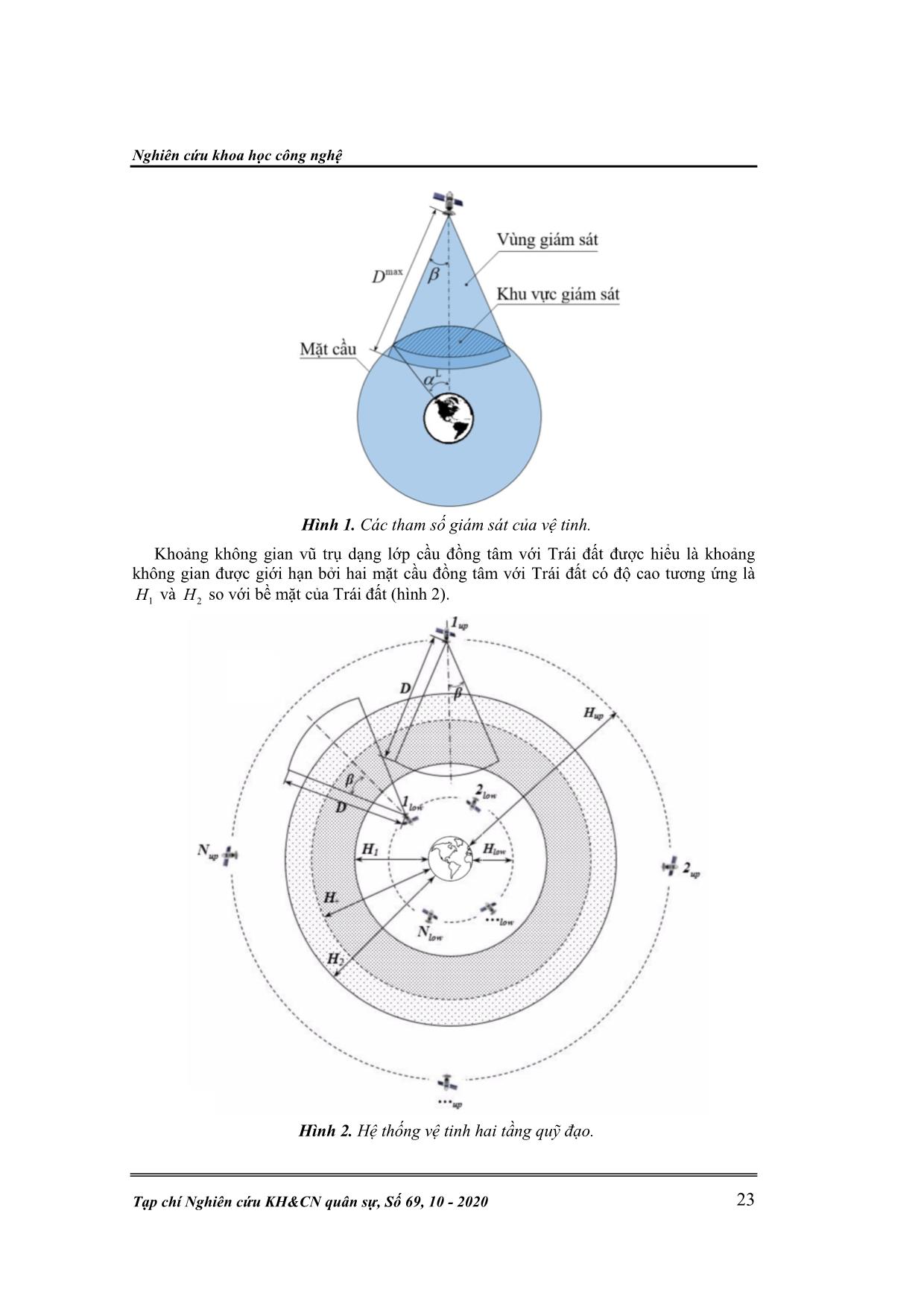
Bài báo đề xuất một cách tiếp cận mới: giám sát liên tục khoảng không
gian vũ trụ dạng lớp cầu đồng tâm với Trái đất dựa trên việc xây dựng hệ thống vệ
tinh hai tầng quỹ đạo có hướng giám sát ngược nhau, trong đó, mỗi tầng vệ tinh là
một hệ thống con độc lập theo mô hình Delta của J.G. Walker (Walker
constellation). Mô hình hóa và phân tích bài toán tối ưu cấu trúc quỹ đạo hệ thống
vệ tinh hai tầng theo tiêu chí tổng vận tốc đặc trưng hệ thống là nhỏ nhất thành các
bài toán dạng truyền thống dễ giải quyết hơn (tối ưu cấu trúc quỹ đạo hệ thống vệ
tinh một tầng theo tiêu chí tổng số vệ tinh trong hệ thống là nhỏ nhất). Bài báo cũng
trình bày cụ thể phương pháp giải các bài toán này. Dựa trên kết quả tính toán
thành lập catalog các phương án cấu trúc quỹ đạo tối ưu của hệ thống vệ tinh hai
tầng đưa ra các phân tích, đánh giá, so sánh kết quả đạt được với cấu trúc hệ thống
vệ tinh một tầng truyền thống.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Tối ưu cấu trúc quỹ đạo hệ thống vệ tinh giám sát liên tục khoảng không gian vũ trụ gần trái đất

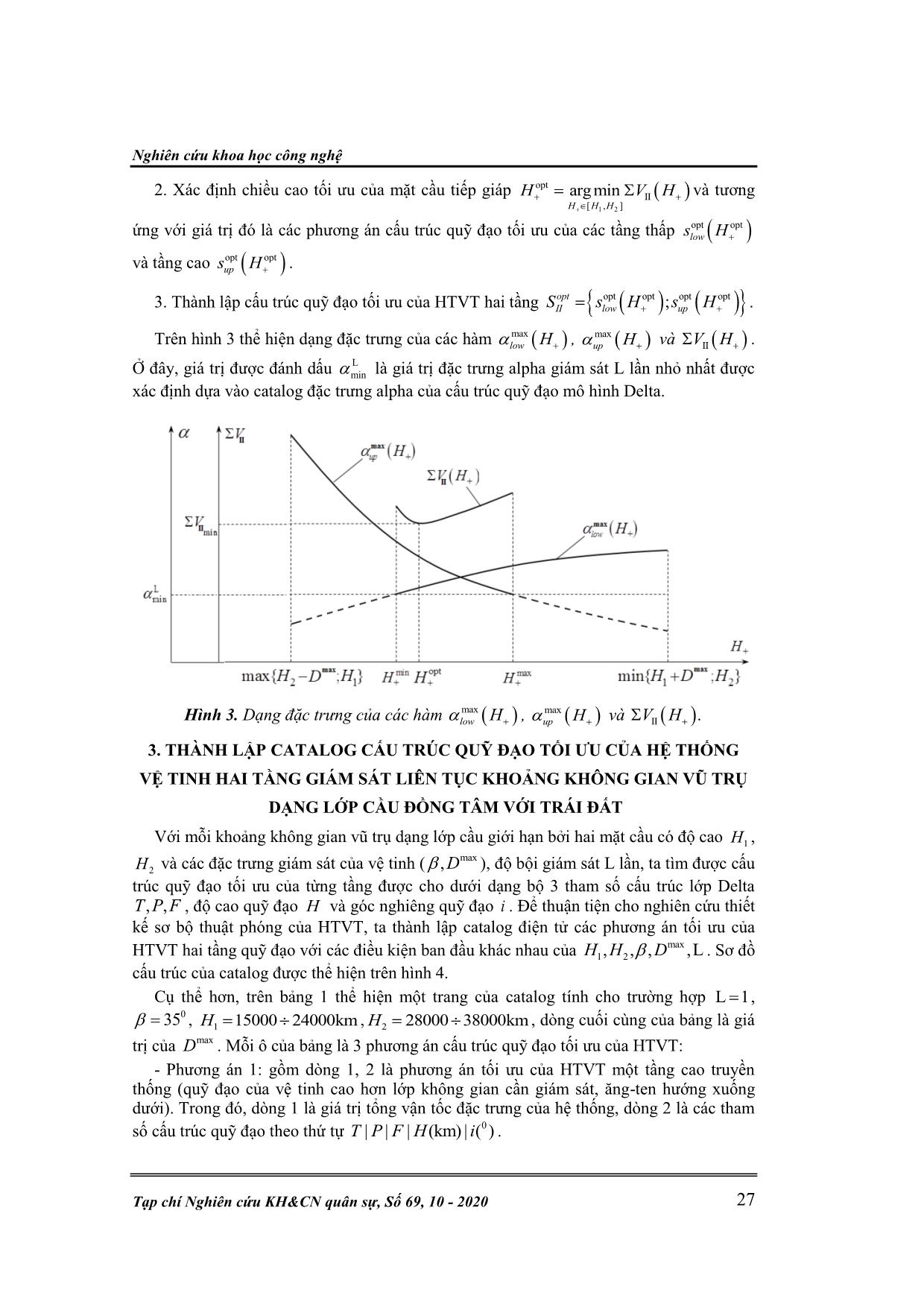
Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 21 TỐI ƯU CẤU TRÚC QUỸ ĐẠO HỆ THỐNG VỆ TINH GIÁM SÁT LIÊN TỤC KHOẢNG KHÔNG GIAN VŨ TRỤ GẦN TRÁI ĐẤT Nguyễn Nam Quý* Tóm tắt: Bài báo đề xuất một cách tiếp cận mới: giám sát liên tục khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất dựa trên việc xây dựng hệ thống vệ tinh hai tầng quỹ đạo có hướng giám sát ngược nhau, trong đó, mỗi tầng vệ tinh là một hệ thống con độc lập theo mô hình Delta của J.G. Walker (Walker constellation). Mô hình hóa và phân tích bài toán tối ưu cấu trúc quỹ đạo hệ thống vệ tinh hai tầng theo tiêu chí tổng vận tốc đặc trưng hệ thống là nhỏ nhất thành các bài toán dạng truyền thống dễ giải quyết hơn (tối ưu cấu trúc quỹ đạo hệ thống vệ tinh một tầng theo tiêu chí tổng số vệ tinh trong hệ thống là nhỏ nhất). Bài báo cũng trình bày cụ thể phương pháp giải các bài toán này. Dựa trên kết quả tính toán thành lập catalog các phương án cấu trúc quỹ đạo tối ưu của hệ thống vệ tinh hai tầng đưa ra các phân tích, đánh giá, so sánh kết quả đạt được với cấu trúc hệ thống vệ tinh một tầng truyền thống. Từ khóa: Thuật phóng tàu vũ trụ; Hệ thống vệ tinh; Cấu trúc quỹ đạo; Hệ thống Delta-Walker. 1. MỞ ĐẦU Tháng 10 năm 1957 vệ tinh Sputnik-1 được tên lửa đẩy R7 phóng lên quỹ đạo thấp của Trái đất, đánh dấu kỷ nguyên chinh phục vũ trụ của loài người. Từ đó đến nay, đã có hàng ngàn vệ tinh nhân tạo được phóng lên các tầng quỹ đạo khác nhau của Trái đất, phục vụ đắc lực cho sự phát triển khoa học kỹ thuật và kinh tế xã hội. Tuy nhiên, cùng với sự phát triển lớn mạnh của ngành khoa học vũ trụ, cũng xuất hiện hàng loạt vấn đề cấp thiết liên quan tới việc giám sát hoạt động của các phương tiện không gian, các vệ tinh nhân tạo, tàu vũ trụ, đặc biệt là việc giám sát rác thải vũ trụ trôi nổi trong một khoảng không gian rộng lớn v.v. Tất cả các nhiệm vụ này, một cách trừu tượng hóa, có thể được hiểu là vấn đề toán học về tối ưu hóa cấu trúc quỹ đạo của hệ thống vệ tinh (HTVT) giám sát liên tục khoảng không gian vũ trụ cho trước có dạng lớp cầu đồng tâm với Trái đất [1, 5, 8, 11, 12]. Tối ưu cấu trúc HTVT được bắt đầu nghiên cứu vào những năm 60 của thế kỷ XX khi giải quyết bài toán giám sát liên tục toàn bộ bề mặt Trái đất. Mô hình đầu tiên được Vargo L.G. và Gobetz F.W. đề xuất khi tối ưu cấu trúc quỹ đạo của hệ thống vệ tinh dạng này gọi là mô hình chuỗi vệ tinh [2, 6]. Mô hình này thuận tiện cho việc tính toán tối ưu hệ thống nhưng yêu cầu tổng số vệ tinh của hệ thống lại rất lớn, điều này hoàn toàn không có lợi cả về mặt kinh tế và kỹ thuật. Vào những năm 70, những nghiên cứu độc lập của nhà khoa học người Nga Можаев Г.В. và nhà khoa học người Mỹ Walker J.G. được đánh giá là có tính đột phá và tạo một bước phát triển mới cho lĩnh vực tối ưu hóa cấu trúc quỹ đạo của HTVT giám sát liên tục toàn bộ bề mặt của Trái đất. Walker đặt tên mô hình cấu trúc quỹ đạo của ông là “hệ thống Delta”[7], còn Можаев gọi đó là “hệ thống động học đối xứng” [10]. Mô hình này là nền tảng cho những nghiên cứu của các nhà khoa học sau này và đã được ứng dụng trong thực tế xây dựng HTVT định vị toàn cầu GPS và Glonass. Phát triển những nghiên cứu của Можаев và Walker, Бырков Б.П. đã công bố những công trình nghiên cứu của ông, và thành lập catalog “đặc tính α” của hệ thống Delta với tổng số vệ tinh trong hệ thống nhỏ hơn 24 và với “độ bội” giám sát từ 1÷5 lần [9]. Trong catalog này, Бырков không những đưa ra cấu trúc tối ưu cho HTVT (cấu trúc có đặc tính α nhỏ nhất) mà còn tính toán đặc tính α cho tất cả các trường hợp có thể có của cấu trúc hệ Tên lửa & Thiết bị bay Nguyễn Nam Quý, “Tối ưu cấu trúc quỹ đạo không gian vũ trụ gần Trái đất.” 22 thống Delta. Vào những năm 2000, với sự trợ giúp đắc lực của máy tính điện tử, khi nghiên cứu bài toán tối ưu cấu trúc quỹ đạo HTVT tầng thấp được xây dựng trên cơ sở hệ thống Delta, Lang T.J. đã công bố một loạt nghiên cứu của ông, mở rộng catalog đặc tính α của hệ thống Delta với tổng số vệ tinh trong hệ thống lên tới 100 [3, 4]. Tuy nhiên, catalog này chưa liệt kê đầy đủ các trường hợp riêng và độ chính xác tính toán còn chưa cao. Tất cả những nghiên cứu của các nhà khoa học kể trên chỉ dừng lại ở việc tối ưu hóa cấu trúc quỹ đạo của HTVT giám sát liên tục, toàn bộ bề mặt Trái đất mà không thể giám sát khoảng không gian vũ trụ, nơi diễn ra nhiều hoạt động truyền dẫn thông tin giữa các vệ tinh và đặc biệt là giám sát chuyển động của rác vũ trụ. Từ thực tế đó, đòi hỏi phải có những nghiên cứu lý thuyết mới, giải quyết bài toán tối ưu cấu trúc quỹ đạo của HTVT có khả năng giám sát liên tục khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất. Liên quan vấn đề này, gần đây có những công bố mới của Разумный Ю.Н., Самусенко О.Е. và Nguyễn Nam Quý, đề xuất phương án cấu trúc HTVT nhiều tầng, mà mỗi tầng vệ tinh được xây dựng dựa trên mô hình Delta của Walker [1, 5, 8, 11, 12] ... tên lửa đẩy tại thời điểm phóng, để đưa các vệ tinh (một lần đẩy có thể đưa cùng lúc nhiều vệ tinh lên quỹ đạo của hệ thống) lên quỹ đạo tròn (với độ cao quỹ đạo và góc nghiêng mặt phẳng quỹ đạo Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 25 định trước) và bố trí vị trí các vệ tinh trên quỹ đạo đó). Đối với HTVT hai tầng quỹ đạo, tổng vận tốc đặc trưng IIV của hệ thống bằng tổng vận tốc đặc trưng tầng quỹ đạo thấp lowV và tầng quỹ đạo cao upV và được tính theo công thức sau [5]: e II e e e e e e e 2 cos 2 cos low low up low low low up up up up R H V V V N R i R R H R H N R i R R H (5) trong đó, e 6371kmR là bán kính Trái đất; 5 -17,29 10 s là vận tốc góc Trái đất; 3 2398 600km /s là tham số hấp dẫn. 2.1.2. Phát biểu bài toán Cho biết giới hạn của khoảng không gian vũ trụ hình lớp cầu đồng tâm với Trái đất 1 2[ , ]H H cần giám sát, các đặc trưng về khả năng giám sát của vệ tinh max( , )D và độ bội giám sát L hãy xác định cấu trúc quỹ đạo tối ưu optIIS của HTVT hai tầng quỹ đạo theo mô hình Delta ( K ) II ,low upS s s để hệ thống đảm bảo giám sát liên tục và toàn phần với tổng vận tốc đặc trưng là nhỏ nhất. Bài toán có thể được phát biểu dưới dạng biểu thức toán học như sau: Cho biết: max1 2, ,L, , ,H H D K Cần tìm: II opt max II II II 1 2argmin | , ,L, , , S S V S H H D K (6) 2.2. Phân tách bài toán tối ưu cấu trúc quỹ đạo hệ thống vệ tinh hai tầng giám sát liên tục khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất và phương pháp giải 2.2.1. Phân tách bài toán Ta tạm thời phân tách khoảng không gian 1 2[ , ]H H thành 2 lớp tiếp giáp nhau bởi mặt cầu có độ cao H thỏa mãn điều kiện 1 2H H H . Các vệ tinh tầng cao (độ cao quỹ đạo upH ) sẽ giám sát lớp cầu dưới 1[ , ]H H và ngược lại các vệ tinh tầng thấp (độ cao quỹ đạo lowH ) sẽ giám sát lớp cầu trên 2[ , ]H H (hình 1). Khi đó, H sẽ trở thành một tham số của bài toán tối ưu. Với mỗi giá trị không đổi của H bài toán tối ưu cấu trúc HTVT hai tầng sẽ được tách ra thành hai bài toán độc lập: Bài toán 1: Tìm cấu trúc tối ưu quỹ đạo HTVT tầng cao đảm bảo nó giám sát liên tục và toàn bộ lớp cầu dưới. Bài toán 2: Tìm cấu trúc tối ưu quỹ đạo HTVT tầng thấp đảm bảo nó giám sát liên tục và toàn bộ lớp cầu trên. Cả hai bài toán này đều có chung một dạng, đó là, tìm cấu trúc tối ưu của HTVT một tầng khi biết trước khoảng không gian dạng lớp cầu mà nó cần giám sát liên tục và toàn phần. Để giải bài toán dạng này, cần giải quyết lần lượt các bài toán nhỏ sau: Bài toán nhỏ 1: Giữa không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất, hãy xác định Tên lửa & Thiết bị bay Nguyễn Nam Quý, “Tối ưu cấu trúc quỹ đạo không gian vũ trụ gần Trái đất.” 26 vị trí mặt cầu tới hạn, tức là mặt cầu mà ở đó khu vực giám sát của hệ thống là nhỏ nhất. Bài toán nhỏ 2: Xác định cấu trúc tối ưu của HTVT một tầng đảm bảo hệ thống giám sát liên tục và toàn phần L lần trên mặt cầu tới hạn với tiêu chí tổng số vệ tinh trong hệ thống là nhỏ nhất. 2.2.2. Phương pháp giải Trên cơ sở phân tách thành những bài toán nhỏ hơn và dữ liệu catalog đặc trưng alpha của mô hình Delta, bài toán tối ưu cấu trúc quỹ đạo HTVT hai tầng giám sát liên tục và toàn bộ L lần khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất có thể giải theo trình tự sau đây. 1. Phân tách khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất thành những mặt cầu có độ cao H ( 1 2H H H ). Với mỗi giá trị của H tiến hành các bước sau: 1.1. Xác định giá trị tối ưu độ cao quỹ đạo của tầng thấp optlowH H và tương ứng là giá trị tới hạn của góc địa tâm khu vực quan sát maxlow H của các vệ tinh tầng thấp. Các đại lượng này là nghiệm của hệ phương trình sau: 22 opt max 2 e 2 emax opt e 2 e opt emax e ( ) arccos 2 sin arcsin low low low low low R H R H D R H R H R H R H (7) 1.2. Xác định giá trị tối ưu độ cao quỹ đạo của tầng cao optupH H và tương ứng là giá trị tới hạn của góc địa tâm khu vực quan sát maxup H của các vệ tinh tầng cao. Các đại lượng này là nghiệm của hệ phương trình sau: 22 opt max 2 e 1 emax opt e 1 e opt emax e ( ) arccos 2 sin arcsin up up up up up R H R H D R H R H R H R H (8) 1.3. Tìm trong catalog đặc trưng alpha của lớp cấu trúc Delta các cấu trúc quỹ đạo tối ưu của HTVT tầng thấp optlows H và tầng cao opt ups H theo tiêu chí tổng số vệ tinh là nhỏ nhất và có đặc trưng alpha L không lớn hơn giá trị tới hạn của góc địa tâm khu vực quan sát tương ứng: opt opt Lopt opt o max L a pt ( ) opt opt m xopt ( ) ( ) arg min ( ) ( ) ( ) arg min ( ) ( ) low low up up low low low low s H H K up up up up K low s H up H s H N H H H H s H N H H H HH H (9) 1.4. Tính tổng vận tốc đặc trưng của từng tầng lowV H , upV H và tổng vận tốc đặc trưng của cả hệ thống II low upV H V H V H . Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 27 2. Xác định chiều cao tối ưu của mặt cầu tiếp giáp 1 2 opt II [ , ] argmin H H H H V H và tương ứng với giá trị đó là các phương án cấu trúc quỹ đạo tối ưu của các tầng thấp opt optlows H và tầng cao opt optups H . 3. Thành lập cấu trúc quỹ đạo tối ưu của HTVT hai tầng opt opt opt opt;optII low upS s H s H . Trên hình 3 thể hiện dạng đặc trưng của các hàm maxlow H , max up H và IIV H . Ở đây, giá trị được đánh dấu Lmin là giá trị đặc trưng alpha giám sát L lần nhỏ nhất được xác định dựa vào catalog đặc trưng alpha của cấu trúc quỹ đạo mô hình Delta. Hình 3. Dạng đặc trưng của các hàm maxlow H , max up H và II .V H 3. THÀNH LẬP CATALOG CẤU TRÚC QUỸ ĐẠO TỐI ƯU CỦA HỆ THỐNG VỆ TINH HAI TẦNG GIÁM SÁT LIÊN TỤC KHOẢNG KHÔNG GIAN VŨ TRỤ DẠNG LỚP CẦU ĐỒNG TÂM VỚI TRÁI ĐẤT Với mỗi khoảng không gian vũ trụ dạng lớp cầu giới hạn bởi hai mặt cầu có độ cao 1H , 2H và các đặc trưng giám sát của vệ tinh ( max, D ), độ bội giám sát L lần, ta tìm được cấu trúc quỹ đạo tối ưu của từng tầng được cho dưới dạng bộ 3 tham số cấu trúc lớp Delta , ,T P F , độ cao quỹ đạo H và góc nghiêng quỹ đạo i . Để thuận tiện cho nghiên cứu thiết kế sơ bộ thuật phóng của HTVT, ta thành lập catalog điện tử các phương án tối ưu của HTVT hai tầng quỹ đạo với các điều kiện ban đầu khác nhau của max1 2, , , ,LH H D . Sơ đồ cấu trúc của catalog được thể hiện trên hình 4. Cụ thể hơn, trên bảng 1 thể hiện một trang của catalog tính cho trường hợp L 1 , 035 , 1 15000 24000kmH , 2 28000 38000kmH , dòng cuối cùng của bảng là giá trị của maxD . Mỗi ô của bảng là 3 phương án cấu trúc quỹ đạo tối ưu của HTVT: - Phương án 1: gồm dòng 1, 2 là phương án tối ưu của HTVT một tầng cao truyền thống (quỹ đạo của vệ tinh cao hơn lớp không gian cần giám sát, ăng-ten hướng xuống dưới). Trong đó, dòng 1 là giá trị tổng vận tốc đặc trưng của hệ thống, dòng 2 là các tham số cấu trúc quỹ đạo theo thứ tự 0| | | (km) | ( )T P F H i . Tên lửa & Thiết bị bay Nguyễn Nam Quý, “Tối ưu cấu trúc quỹ đạo không gian vũ trụ gần Trái đất.” 28 B ả n g 1 . C ấ u trú c q u ỹ đ ạ o tố i ư u củ a H T V T h a i tầ n g kh i L = 1 và β = 3 5 0. Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 29 - Phương án 2: gồm dòng 3, 4 là phương án tối ưu của HTVT một tầng thấp truyền thống (quỹ đạo của vệ tinh thấp hơp lớp không gian cần giám sát, ăng-ten hướng lên trên). Trong đó, dòng 3 là giá trị tổng vận tốc đặc trưng của hệ thống, dòng 4 là các tham số cấu trúc quỹ đạo theo thứ tự 0| | | (km) | ( )T P F H i . - Phương án 3: gồm dòng 5, 6, 7 là phương án tối ưu của HTVT hai tầng. Trong đó, dòng 5 là giá trị tổng vận tốc đặc trưng của hệ thống, dòng 6 là tham số cấu trúc quỹ đạo của tầng cao theo thứ tự 0| | | (km) | ( )up up up up upT P F H i , dòng 7 là tham số cấu trúc quỹ đạo của tầng thấp theo thứ tự 0| | | (km) | ( )low low low low lowT P F H i . Hình 4. Sơ đồ catalog các phương án tối ưu cấu trúc quỹ đạo hệ thống vệ tinh hai tầng. Catalog này cho phép so sánh (theo tiêu chí tổng vận tốc đặc trưng của hệ là nhỏ nhất) cấu trúc quỹ đạo của HTVT giám sát liên tục và toàn phần khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất ở các phương án khi hệ thống chỉ có một tầng theo cách tiếp cận truyền thống và hệ thống hai tầng quỹ đạo theo đề xuất của bài báo. Điều này được thể hiện trên bảng 1, với các ô có nền màu xanh là hệ thống 2 tầng tốt hơn, các ô có nền màu trắng là hệ thống một tầng thấp tốt hơn còn ô có nền màu vàng là hệ thống một tầng cao tốt hơn. Phù hợp với giá trị ban đầu của các tham số đầu vào mà ta có sự lựa chọn cấu trúc quỹ đạo cho hệ thống một cách hợp lý ở dạng một tầng hay hai tầng quỹ đạo. Từ bảng 1 có thể thấy, phương án cấu trúc hệ thống hai tầng quỹ đạo tốt hơn là một tầng khi lớp không gian vũ trụ cần giám sát có bề dày lớn, giới hạn 1H nhỏ hơn và cự ly giám sát không xa. Phương án một tầng cao tốt hơn khi khoảng không gian cần giám sát có bề dày mỏng, cự ly giám sát của vệ tinh lớn, 1H lớn hơn nhưng 2H lại nhỏ. 4. KẾT LUẬN Dựa trên mô hình cấu trúc Delta của Walker, bài báo đã đưa ra phương pháp xây dựng cấu trúc quỹ đạo tối ưu của HTVT hai tầng giám sát liên tục và toàn bộ khoảng không gian CATALOG cấu trúc quỹ đạo tối ưu hệ thống vệ tinh hai tầng giám sát liên tục và toàn bộ L lần khoảng không gian vũ trụ dạng lớp cầu đồng tâm với trái đất Tập 1 L=1 P h ần 1 β = 3 0 0 P h ần 2 β = 3 5 0 P h ần 3 β = 4 0 0 Tập 4 L=4 Tập 2 L=2 Tập 3 L=3 P h ần 6 β = 4 5 0 № trang 1 2 3 4 5 6 7 8 H1, km 0 5000 10000 15000 20000 25000 30000 35000 P h ần 4 β = 3 5 0 P h ần 5 β = 4 0 0 P h ần 7 β = 4 0 0 P h ần 8 β = 4 5 0 P h ần 9 β = 5 0 0 P h ần 1 0 β = 4 5 0 P h ần 1 1 β = 5 0 0 P h ần 1 2 β = 5 5 0 Tên lửa & Thiết bị bay Nguyễn Nam Quý, “Tối ưu cấu trúc quỹ đạo không gian vũ trụ gần Trái đất.” 30 vũ trụ dạng lớp cầu đồng tâm với Trái đất theo tiêu chí tổng vận tốc đặc trưng của hệ thống là nhỏ nhất. Tùy thuộc vào các điều kiện ban đầu về kích thước của lớp không gian vũ trụ cần giám sát và đặc trưng thiết bị giám sát lắp đặt trên vệ tinh mà cấu trúc hai tầng quỹ đạo thể hiện tốt hơn hay kém hơn cấu trúc một tầng truyền thống. Nghiên cứu này đề xuất một cách tiếp cận mới, mang tính lý thuyết, trong việc giải quyết bài toán giám sát khoảng không gian vũ trụ dạng lớp cầu đồng tâm với Trái đất, là bài toán cơ bản bước đầu cần giải quyết trong quá trình thiết kế sơ bộ thuật phóng của HTVT, đặc biệt với các HTVT mini (nanosatellite) yêu cầu tổng số vệ tinh trong hệ thống lớn. TÀI LIỆU THAM KHẢO [1]. Daniele Mortari, Yury N. Razoumny, Oleg E. Samusenko, Viktoria D. Novikova, Nguyen Nam Quy, “The Algorithm for Solving the Task of Choosing the Optimal Two-Tier Satellite Constellation for Continuous Coverage of the Spherical Layer of Near-Earth Space”, Published by UNIVELT, Inc., USA, Advances in the Astronautical Sciences, 2020, vol.170, pp.463-473. [2]. Gobetz F.W., “Satellite networks for global coverage”, Advances in astronautical sciences, Vol. 9(1963), pp. 134-156. [3]. Lang T.J., “Optimal low earth orbit constellations for continuous global coverage”, AAS/AIAA Astrodynamics Specialist Conference, Victoria, BC, Aug. 16-19 1993, No. 597, 17 p. [4]. Lang T.J., “Walker Constellations to Minimize Revisit Time in Low Earth Orbit”, 13- th AAS/AIAA Space Flight Mechanics Meeting, Ponce, Puerto Rico, 9–13 February, 2003, paper AAS 03-178. [5]. Razoumny Yu.N., “Fundamentals of the Route Theory for Satellite Constellation Design for Earth Discontinuous Coverage Part 3: Low-Cost Earth Observation with Minimal Satellite Swath”, Acta Astronautica, 2016, vol. 129, pp. 447–458. [6]. Vargo L.G., “Orbital patterns of satellite systems”, The Journal of the Astronautical Sciences, Vol. 7, № 4(1960), pp.78-86. [7]. Walker J.G., “Satellite Constellations”, Journal of the British Interplanetary Society, Vol. 24(1984), pp. 369–384. [8]. Yury N. Razoumny, Oleg Samusenko, Nguyen Nam Quy, “Satellite Constellation Design for Near Earth Space Coverage Basing on Two-Tier Satellite Structures”, Advances in the Astronautical Sciences, 2017, Vol. 161, pp. 1142-1149. [9]. БырковБ.П., “Каталогcистемынепрерывногомногократногообзорасферы”, т.1-т.5, Москва, 1977. [10]. МожаевГ.В., “Задачаонепрерывном обзоре Земли и кинематически правильные спутниковые системы”,I. Космические исследования, 1972, т. 10, вып. 6, с. 833–840. [11]. Разумный Ю.Н., Самусенко О.Е., Нгуен Нам Куи, “Анализ оптимальных вариантов двухъярусных спутниковых систем непрерывного обзора сферического слоя околоземного космического пространства”, Вестник Московского авиационного института, 2018, Т.25, № 3, с.171-181. [12]. Разумный Ю.Н., Самусенко О.Е., Нгуен Нам Куи, “О задаче оптимизации орбитальной структуры многоярусных спутниковых систем непрерывного обзора околоземного пространства”, Известия высших учебных заведений. Машиностроение, 2018, №4(697), c. 61-72. Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 69, 10 - 2020 31 ABSTRACT OPTIMIZATION OF ORBITAL STRUCTURE OF SATELLITE CONSTELLATIONS TO PROVIDE CONTINUOUS COVERAGE OF NEAR-EARTH SPACE SPHERICAL LAYER In the paper, a completely new approach: continuous monitoring of near-Earth space spherical layer based on the construction of two-tiers orbiting satellite constellation with opposite viewing directions, in which each the satellite tier is an independent subsystem that follows the "Delta-system" model of WalkerJ.G. (Walker constellation) is proposed. Modeling and analyzing the problem of optimizing the structure of two-tiers satellite constellations in orbit according to the criterion of the total system characteristic velocity is the smallest into the more traditional problems which are easier to solve - optimizing the system structure one- tier satellite constellation according to the criteria that the total number of satellites in the system is the smallest. In this article, methods of solving these problems are also presented. Based on the results of the calculation and establishment of the catalog of the optimal orbital structure plans of the two-tier satellite constellation, the analysis, evaluation and comparing the achieved results with the satellite constellation structure traditional one-tier are made. Keywords: Spacecraft ballistics; Satellite constellation; Orbital structure; Walker constellation. Nhận bài ngày 21 tháng 6 năm 2020 Hoàn thiện ngày 18 tháng 8 năm 2020 Chấp nhận đăng ngày 15 tháng 10 năm 2020 Địa chỉ: Học viện Kỹ thuật quân sự. * Email: sky_moscow@mail.ru.
File đính kèm:
 toi_uu_cau_truc_quy_dao_he_thong_ve_tinh_giam_sat_lien_tuc_k.pdf
toi_uu_cau_truc_quy_dao_he_thong_ve_tinh_giam_sat_lien_tuc_k.pdf

