Tính toán mô phỏng detector bán dẫn CdZnTe bằng phương pháp monte carlo

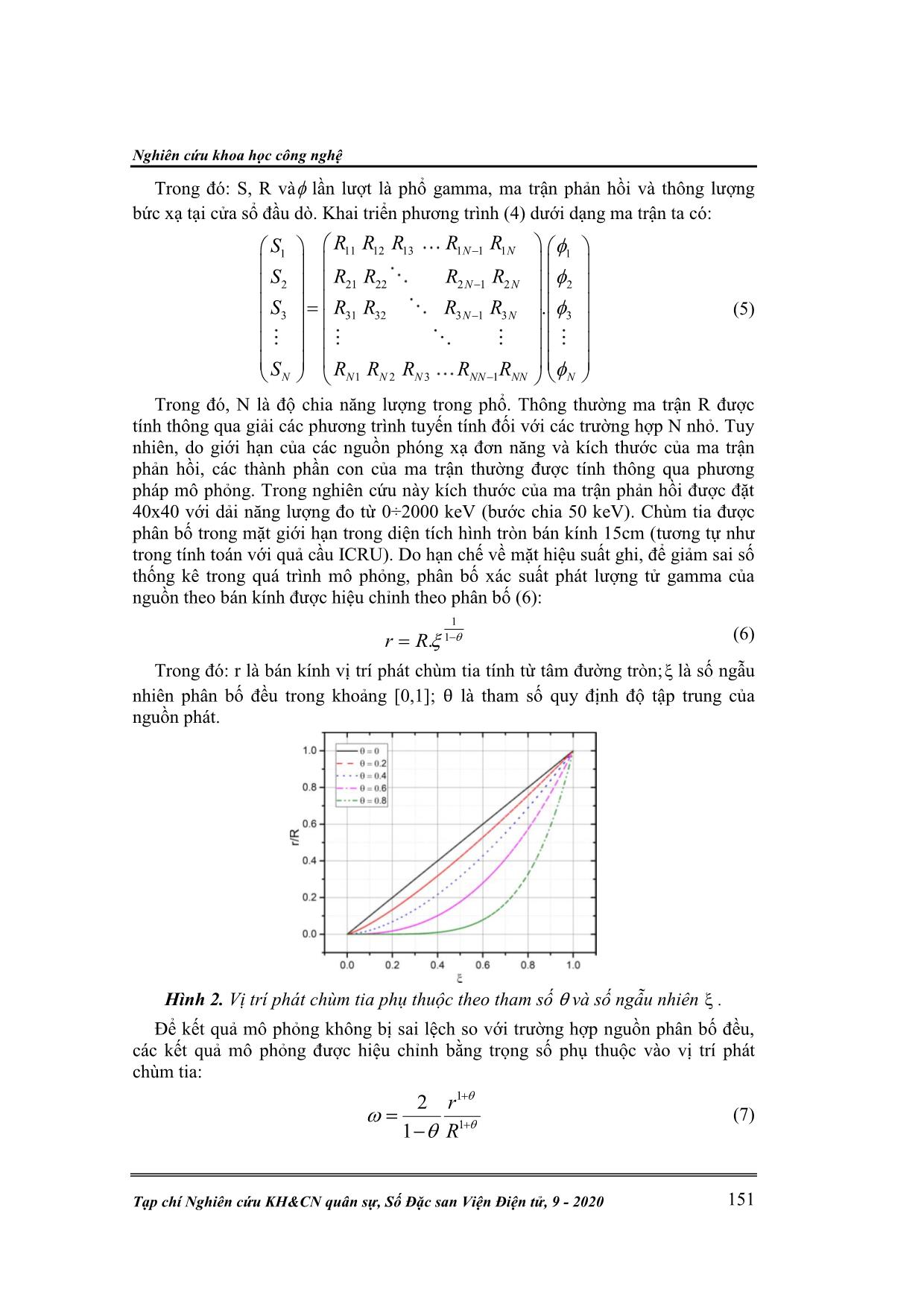
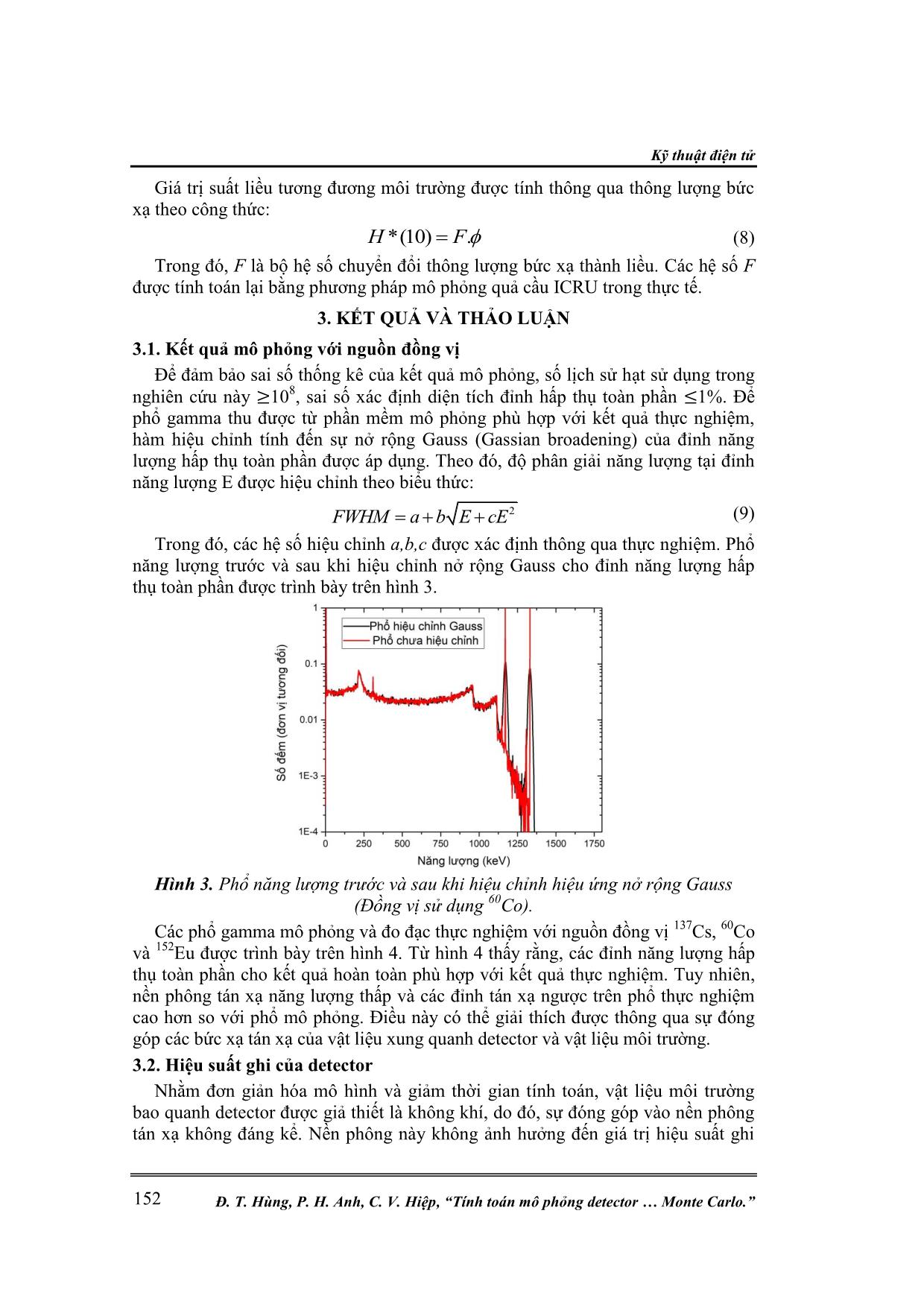
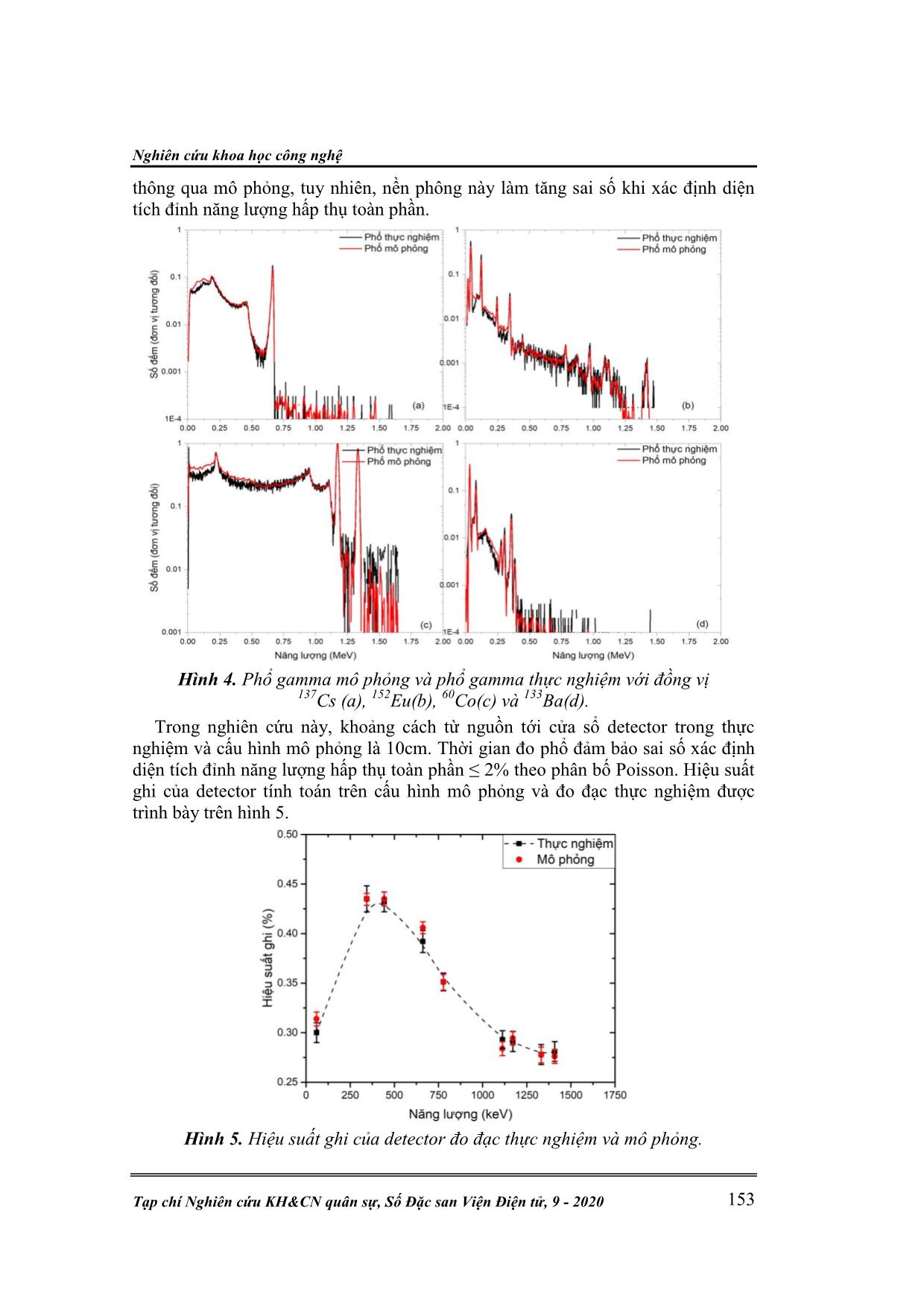
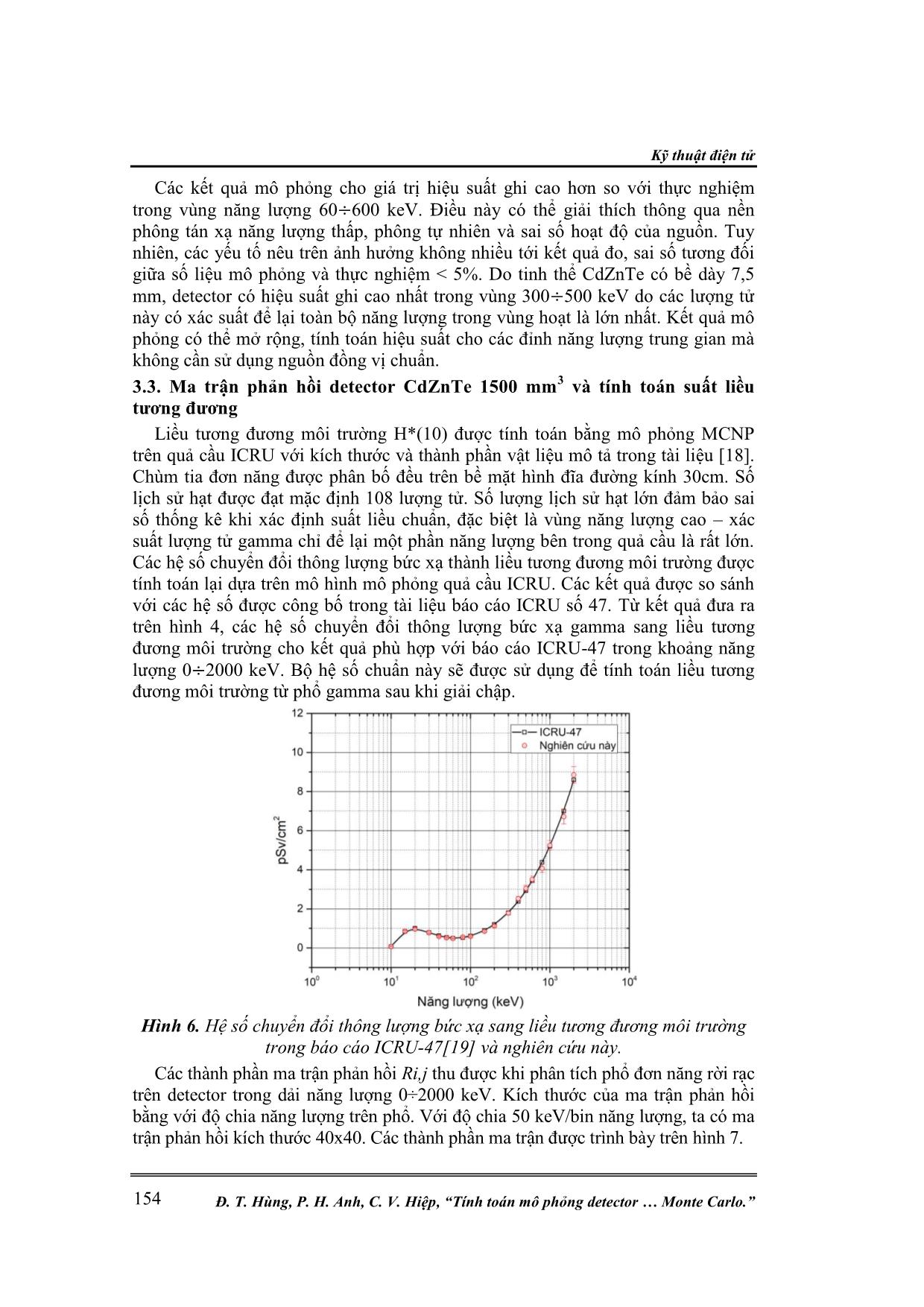
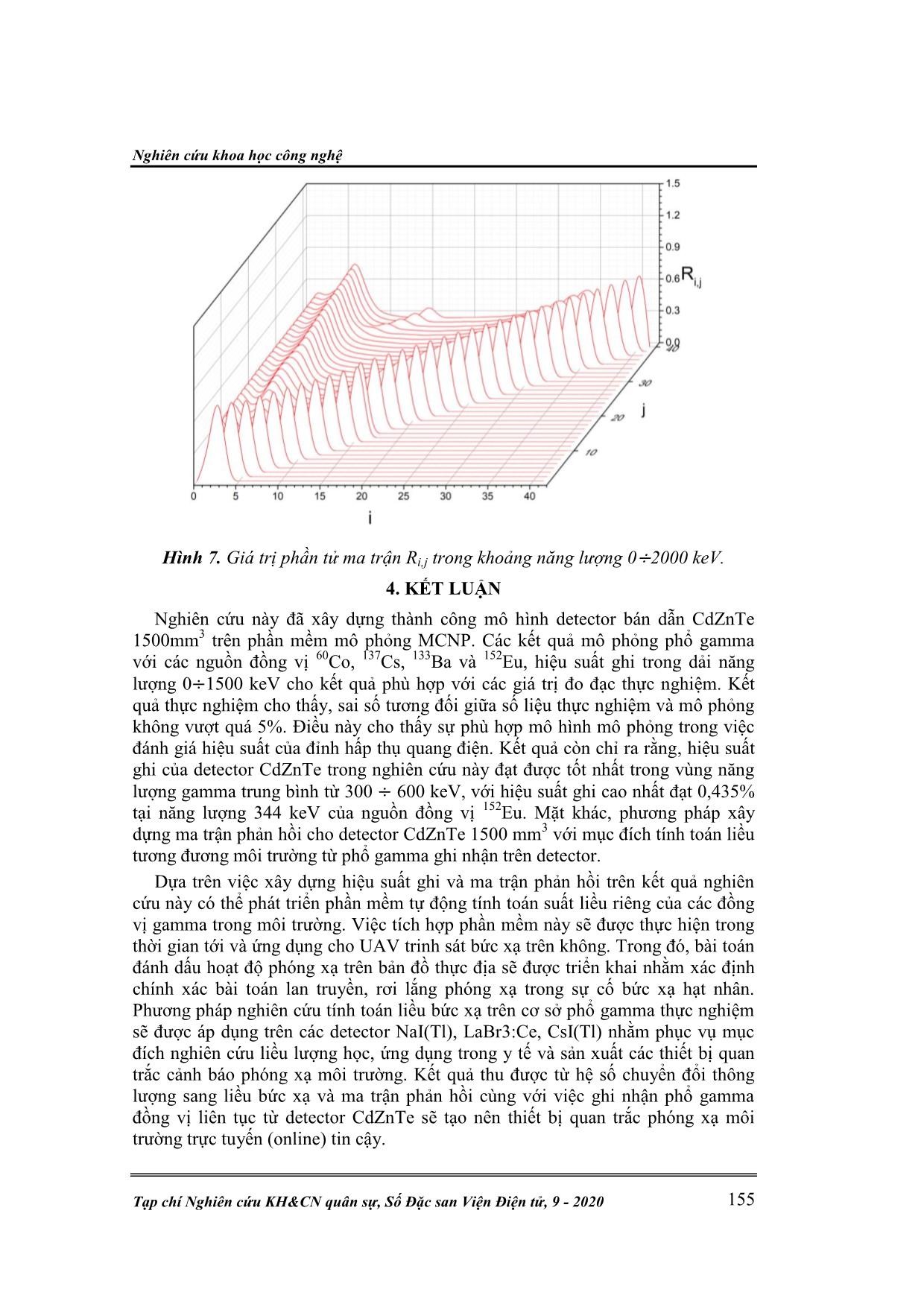
Kỹ thuật điện tử 
Đ. T. Hùng, P. H. Anh, C. V. Hiệp, “Tính toán mô phỏng detector  Monte Carlo.” 148 
TÍNH TOÁN MÔ PHỎNG DETECTOR BÁN DẪN CdZnTe BẰNG 
PHƢƠNG PHÁP MONTE CARLO 
Đinh Tiến Hùng1*, Phan Huy Anh2, Cao Văn Hiệp1 
Tóm tắt: Bài báo này trình bày mô hình, kết quả tính toán mô phỏng thu được từ 
việc sử dụng phương pháp Monte Carlo trong nghiên cứu mô phỏng phổ gamma, 
tính toán hiệu suất ghi, ma trận phản hồi cho detector bán dẫn CdZnTe(CZT) kích 
thước 1500 mm3 trang bị trên thiết bị bay trinh sát phóng xạ UAV. Kết quả tính toán 
mô phỏng được so sánh với kết quả thực nghiệm đối với 4 nguồn đồng vị phóng xạ 
137
Cs, 
60
Co, 
133
Ba và 
152Eu. Các kết quả so sánh cho thấy rằng phổ gamma, hiệu suất 
ghi tuyệt đối của detector phù hợp tốt với các kết quả đo thực nghiệm. Mô hình 
detector CdZnTe trong nghiên cứu này được áp dụng xây dựng đường cong hiệu 
suất và tính toán liều bức xạ trên cơ sở phổ gamma thu được. 
Từ khóa: Thiết bị bay không người lái UAV; Đầu ghi bán dẫn CdZnTe; Phương pháp Monte Carlo; Ma trận 
phản hồi; Suất liều gamma môi trường. 
1. MỞ ĐẦU 
Trong nhiều lĩnh vực của khoa học hạt nhân ứng dụng, các detector ghi bức xạ 
gamma được sử dụng để đo phổ năng lượng gamma, phân tích nhận diện đồng vị, 
xác định hàm lượng đồng vị phóng xạ có trong mẫu, môi trường. Việc sử dụng 
detector bán dẫn siêu tinh khiết đã mang lại kết quả chính xác hơn trong việc ghi 
nhận bức xạ gamma trong dải năng lượng rộng so với các loại detector nhấp nháy 
truyền thống. Tuy nhiên, nhược điểm của các hệ phổ kế sử dụng detector bán dẫn 
loại này là nhiệt độ làm việc thấp, đòi hỏi các hệ thống làm lạnh bằng ni tơ lỏng 
(-196℃). Trong các hệ phổ kế đòi hỏi sự chính xác cao, hoạt động trong điều kiện 
nhiệt độ phòng trong thời gian dài, các detector bán dẫn CdZnTe (Cadmium-Zinc-
Telluride) [1] được ưu tiên sử dụng do loại detector này sở hữu những ưu điểm 
vượt trội so với các detector bán dẫn Silicon [2, 3] và Germanium [2, 3]. Tuy 
nhiên, do giới hạn trong công nghệ chế tạo tinh thể, thể tích vùng nhạy của các 
detector CdZnTe chỉ dừng lại ở mức vừa và nhỏ. 
Trong quá trình khảo sát mẫu, đặc biệt là đối với các mẫu môi trường, do hoạt 
độ phóng xạ trong mẫu rất thấp (cỡ ppm) để số đếm đảm bảo về mặt thống kê cần 
đo trong thời gian rất dài, lượng mẫu lớn. Việc chuẩn hiệu suất với các detector đo 
môi trường là mối quan tâm hàng đầu. Có nhiều phương pháp được đưa ra để giải 
quyết vấn đề này: i) xây dựng đường cong hiệu suất bằng số liệu đo đạc thực 
nghiệm [4, 5]; ii) xây dựng các công thức tính toán hiệu suất bằng phương pháp 
giải tích kết hợp các tham số hình học của detector và mẫu [6, 7]; iii) sử dụng 
phương pháp mô phỏng [8-10]. Quá trình xác định đường cong hiệu suất bằng thực 
nghiệm và thiết lập công thức giải tích rất tốn kém và mất nhiều thời gian, đặc biệt 
là các detector có thể tích vùng hoạt nhỏ. Trong nghiên cứu này, hiệu suất ghi của 
detector được tính toán thông qua phương pháp mô phỏng Monte Carlo trên phần 
mềm MCNP-5 trong dải năng lượng 0÷2000 keV. Các kết quả mô phỏng với 
nguồn đồng vị 137Cs, 60Co, 133Ba và 152Eu được so sánh với thực nghiệm. Mô hình 
detector CdZnTe được áp dụng trong quá trình xây dựng hàm và ma trận phản hồi 
với mục đích tính toán liều bức xạ từ phổ gamma thu được. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 149 
2. ĐỐI TƢỢNG VÀ PHƢƠNG PHÁP NGHIÊN CỨU 
 2.1. Phƣơng pháp mô phỏng Monte Carlo và phần mềm MCNP 
Phương pháp Monte Carlo [11, 12] là một phương pháp giải số cho bài toán mà 
mô phỏng sự tương tác của những vật thể này với những vật thể khác hay là với 
môi trường dựa trên các mối quan hệ giữa vật thể với vật thể và vật thể với môi 
trường đơn giản. Phương pháp này mô hình hóa tự nhiên thông qua sự mô phỏng 
trực tiếp các lý thuyết động học cần thiết dựa theo yêu cầu của hệ. Phương pháp 
Monte Carlo giải quyết các mô hình tương tác bằng tập hợp các số ngẫu nhiên và 
các hàm phân bố mật độ xác suất đặc trưng cho các quá trình vật lý xảy ra trong 
môi trường. Phần mềm MCNP [12] là phần mềm dựa trên phương pháp Monte 
Carlo được phát triển bởi nhóm Monte Carlo và sau này là nhóm Radiation 
Transport (Nhóm X-6) của phòng Vật lý lý thuyết ứng dụng ở phòng Thí nghiệm 
quốc gia Los – Alamos (Mỹ) để mô phỏng các quá trình vật lý hạt nhân đối với 
notron, gamma, electron mang tính thống kê (các quá trình phân rã hạt nhân, tương 
tác giữa các tia bức xạ với vật chất, thông lượng notron,...). MCNP sử dụng các thư 
viện dữ liệu của các quá trình hạt nhân bao gồm thư viện ENSDF [13] (Evaluated 
Nuclear Data File), ACTI [14] (Advanced Computational Technology Initiative), 
ENDL [15] (Evaluated Nuclear Data Library), EPDL [16] (Evaluated Photon Data 
Library), ACTL [17] (Activation Library), các quy luật phân bố thống kê, gieo số 
ngẫu nhiên, ghi lại các sự kiện của một hạt trong suốt quá trình kể từ khi phát ra từ 
nguồn đến hết thời gian sống c ... h vùng hoạt của đầu dò. 
2.3.2. Ma trận phản hồi và phương pháp tính toán liều tương đương môi trường 
Liều tương đương môi trường (Ambient dose equivalent) – H*(d) tại một điểm 
trong trường bức xạ được định nghĩa bởi Ủy ban Quốc tế về Đo lường và Đơn vị 
Bức xạ (International Commission on Radiation Units and Measurements – ICRU) 
trong tài liệu số 103 [18]. Đối với các tia gamma có năng lượng lớn hơn 15 keV 
đều được xem xét là bức xạ có khả năng đâm xuyên cao, vì vậy, độ sâu 10 mm 
(suất liều tương ứng là H*(10)) thường được sử dụng để đánh giá tác động của 
trường bức xạ đối với các cơ quan trong cơ thể. 
Phương pháp chuyển phổ thành liều sử dụng ma trận phản hồi dựa vào mối 
quan hệ giữa phổ gamma thu được trên hệ phổ kế và thông lượng bức xạ đến cửa 
sổ đầu dò: 
.S R (4) 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 151 
Trong đó: S, R và lần lượt là phổ gamma, ma trận phản hồi và thông lượng 
bức xạ tại cửa sổ đầu dò. Khai triển phương trình (4) dưới dạng ma trận ta có: 
11 12 13 1 1 11 1
21 22 2 1 22 2
3 31 32 3 1 3 3
1 2 3 1
.
N N
N N
N N
N N N N NN NN N
R R R R RS
R R R RS
S R R R R
S R R R R R




 (5) 
Trong đó, N là độ chia năng lượng trong phổ. Thông thường ma trận R được 
tính thông qua giải các phương trình tuyến tính đối với các trường hợp N nhỏ. Tuy 
nhiên, do giới hạn của các nguồn phóng xạ đơn năng và kích thước của ma trận 
phản hồi, các thành phần con của ma trận thường được tính thông qua phương 
pháp mô phỏng. Trong nghiên cứu này kích thước của ma trận phản hồi được đặt 
40x40 với dải năng lượng đo từ 0÷2000 keV (bước chia 50 keV). Chùm tia được 
phân bố trong mặt giới hạn trong diện tích hình tròn bán kính 15cm (tương tự như 
trong tính toán với quả cầu ICRU). Do hạn chế về mặt hiệu suất ghi, để giảm sai số 
thống kê trong quá trình mô phỏng, phân bố xác suất phát lượng tử gamma của 
nguồn theo bán kính được hiệu chỉnh theo phân bố (6): 
1
1.r R  (6) 
Trong đó: r là bán kính vị trí phát chùm tia tính từ tâm đường tròn; là số ngẫu 
nhiên phân bố đều trong khoảng [0,1]; θ là tham số quy định độ tập trung của 
nguồn phát. 
Hình 2. Vị trí phát chùm tia phụ thuộc theo tham số θ và số ngẫu nhiên  . 
Để kết quả mô phỏng không bị sai lệch so với trường hợp nguồn phân bố đều, 
các kết quả mô phỏng được hiệu chỉnh bằng trọng số phụ thuộc vào vị trí phát 
chùm tia: 
1
1
2
1
r
R




 (7) 
Kỹ thuật điện tử 
Đ. T. Hùng, P. H. Anh, C. V. Hiệp, “Tính toán mô phỏng detector  Monte Carlo.” 152 
Giá trị suất liều tương đương môi trường được tính thông qua thông lượng bức 
xạ theo công thức: 
*(10) .H F (8) 
Trong đó, F là bộ hệ số chuyển đổi thông lượng bức xạ thành liều. Các hệ số F 
được tính toán lại bằng phương pháp mô phỏng quả cầu ICRU trong thực tế. 
3. KẾT QUẢ VÀ THẢO LUẬN 
3.1. Kết quả mô phỏng với nguồn đồng vị 
Để đảm bảo sai số thống kê của kết quả mô phỏng, số lịch sử hạt sử dụng trong 
nghiên cứu này ≥108, sai số xác định diện tích đỉnh hấp thụ toàn phần ≤1%. Để 
phổ gamma thu được từ phần mềm mô phỏng phù hợp với kết quả thực nghiệm, 
hàm hiệu chỉnh tính đến sự nở rộng Gauss (Gassian broadening) của đỉnh năng 
lượng hấp thụ toàn phần được áp dụng. Theo đó, độ phân giải năng lượng tại đỉnh 
năng lượng E được hiệu chỉnh theo biểu thức: 
2 FWHM a b E cE (9) 
Trong đó, các hệ số hiệu chỉnh a,b,c được xác định thông qua thực nghiệm. Phổ 
năng lượng trước và sau khi hiệu chỉnh nở rộng Gauss cho đỉnh năng lượng hấp 
thụ toàn phần được trình bày trên hình 3. 
Hình 3. Phổ năng lượng trước và sau khi hiệu chỉnh hiệu ứng nở rộng Gauss 
(Đồng vị sử dụng 60Co). 
Các phổ gamma mô phỏng và đo đạc thực nghiệm với nguồn đồng vị 137Cs, 60Co 
và 
152Eu được trình bày trên hình 4. Từ hình 4 thấy rằng, các đỉnh năng lượng hấp 
thụ toàn phần cho kết quả hoàn toàn phù hợp với kết quả thực nghiệm. Tuy nhiên, 
nền phông tán xạ năng lượng thấp và các đỉnh tán xạ ngược trên phổ thực nghiệm 
cao hơn so với phổ mô phỏng. Điều này có thể giải thích được thông qua sự đóng 
góp các bức xạ tán xạ của vật liệu xung quanh detector và vật liệu môi trường. 
3.2. Hiệu suất ghi của detector 
Nhằm đơn giản hóa mô hình và giảm thời gian tính toán, vật liệu môi trường 
bao quanh detector được giả thiết là không khí, do đó, sự đóng góp vào nền phông 
tán xạ không đáng kể. Nền phông này không ảnh hưởng đến giá trị hiệu suất ghi 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 153 
thông qua mô phỏng, tuy nhiên, nền phông này làm tăng sai số khi xác định diện 
tích đỉnh năng lượng hấp thụ toàn phần. 
Hình 4. Phổ gamma mô phỏng và phổ gamma thực nghiệm với đồng vị 
137
Cs (a), 
152
Eu(b), 
60
Co(c) và 
133
Ba(d). 
Trong nghiên cứu này, khoảng cách từ nguồn tới cửa sổ detector trong thực 
nghiệm và cấu hình mô phỏng là 10cm. Thời gian đo phổ đảm bảo sai số xác định 
diện tích đỉnh năng lượng hấp thụ toàn phần ≤ 2% theo phân bố Poisson. Hiệu suất 
ghi của detector tính toán trên cấu hình mô phỏng và đo đạc thực nghiệm được 
trình bày trên hình 5. 
Hình 5. Hiệu suất ghi của detector đo đạc thực nghiệm và mô phỏng. 
Kỹ thuật điện tử 
Đ. T. Hùng, P. H. Anh, C. V. Hiệp, “Tính toán mô phỏng detector  Monte Carlo.” 154 
Các kết quả mô phỏng cho giá trị hiệu suất ghi cao hơn so với thực nghiệm 
trong vùng năng lượng 60÷600 keV. Điều này có thể giải thích thông qua nền 
phông tán xạ năng lượng thấp, phông tự nhiên và sai số hoạt độ của nguồn. Tuy 
nhiên, các yếu tố nêu trên ảnh hưởng không nhiều tới kết quả đo, sai số tương đối 
giữa số liệu mô phỏng và thực nghiệm < 5%. Do tinh thể CdZnTe có bề dày 7,5 
mm, detector có hiệu suất ghi cao nhất trong vùng 300÷500 keV do các lượng tử 
này có xác suất để lại toàn bộ năng lượng trong vùng hoạt là lớn nhất. Kết quả mô 
phỏng có thể mở rộng, tính toán hiệu suất cho các đỉnh năng lượng trung gian mà 
không cần sử dụng nguồn đồng vị chuẩn. 
3.3. Ma trận phản hồi detector CdZnTe 1500 mm3 và tính toán suất liều 
tương đương 
Liều tương đương môi trường H*(10) được tính toán bằng mô phỏng MCNP 
trên quả cầu ICRU với kích thước và thành phần vật liệu mô tả trong tài liệu [18]. 
Chùm tia đơn năng được phân bố đều trên bề mặt hình đĩa đường kính 30cm. Số 
lịch sử hạt được đạt mặc định 108 lượng tử. Số lượng lịch sử hạt lớn đảm bảo sai 
số thống kê khi xác định suất liều chuẩn, đặc biệt là vùng năng lượng cao – xác 
suất lượng tử gamma chỉ để lại một phần năng lượng bên trong quả cầu là rất lớn. 
Các hệ số chuyển đổi thông lượng bức xạ thành liều tương đương môi trường được 
tính toán lại dựa trên mô hình mô phỏng quả cầu ICRU. Các kết quả được so sánh 
với các hệ số được công bố trong tài liệu báo cáo ICRU số 47. Từ kết quả đưa ra 
trên hình 4, các hệ số chuyển đổi thông lượng bức xạ gamma sang liều tương 
đương môi trường cho kết quả phù hợp với báo cáo ICRU-47 trong khoảng năng 
lượng 0÷2000 keV. Bộ hệ số chuẩn này sẽ được sử dụng để tính toán liều tương 
đương môi trường từ phổ gamma sau khi giải chập. 
Hình 6. Hệ số chuyển đổi thông lượng bức xạ sang liều tương đương môi trường 
trong báo cáo ICRU-47[19] và nghiên cứu này. 
Các thành phần ma trận phản hồi Ri,j thu được khi phân tích phổ đơn năng rời rạc 
trên detector trong dải năng lượng 0÷2000 keV. Kích thước của ma trận phản hồi 
bằng với độ chia năng lượng trên phổ. Với độ chia 50 keV/bin năng lượng, ta có ma 
trận phản hồi kích thước 40x40. Các thành phần ma trận được trình bày trên hình 7. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 155 
Hình 7. Giá trị phần tử ma trận Ri,j trong khoảng năng lượng 0÷2000 keV. 
4. KẾT LUẬN 
Nghiên cứu này đã xây dựng thành công mô hình detector bán dẫn CdZnTe 
1500mm
3
 trên phần mềm mô phỏng MCNP. Các kết quả mô phỏng phổ gamma 
với các nguồn đồng vị 60Co, 137Cs, 133Ba và 152Eu, hiệu suất ghi trong dải năng 
lượng 0÷1500 keV cho kết quả phù hợp với các giá trị đo đạc thực nghiệm. Kết 
quả thực nghiệm cho thấy, sai số tương đối giữa số liệu thực nghiệm và mô phỏng 
không vượt quá 5%. Điều này cho thấy sự phù hợp mô hình mô phỏng trong việc 
đánh giá hiệu suất của đỉnh hấp thụ quang điện. Kết quả còn chỉ ra rằng, hiệu suất 
ghi của detector CdZnTe trong nghiên cứu này đạt được tốt nhất trong vùng năng 
lượng gamma trung bình từ 300 ÷ 600 keV, với hiệu suất ghi cao nhất đạt 0,435% 
tại năng lượng 344 keV của nguồn đồng vị 152Eu. Mặt khác, phương pháp xây 
dựng ma trận phản hồi cho detector CdZnTe 1500 mm3 với mục đích tính toán liều 
tương đương môi trường từ phổ gamma ghi nhận trên detector. 
Dựa trên việc xây dựng hiệu suất ghi và ma trận phản hồi trên kết quả nghiên 
cứu này có thể phát triển phần mềm tự động tính toán suất liều riêng của các đồng 
vị gamma trong môi trường. Việc tích hợp phần mềm này sẽ được thực hiện trong 
thời gian tới và ứng dụng cho UAV trinh sát bức xạ trên không. Trong đó, bài toán 
đánh dấu hoạt độ phóng xạ trên bản đồ thực địa sẽ được triển khai nhằm xác định 
chính xác bài toán lan truyền, rơi lắng phóng xạ trong sự cố bức xạ hạt nhân. 
Phương pháp nghiên cứu tính toán liều bức xạ trên cơ sở phổ gamma thực nghiệm 
sẽ được áp dụng trên các detector NaI(Tl), LaBr3:Ce, CsI(Tl) nhằm phục vụ mục 
đích nghiên cứu liều lượng học, ứng dụng trong y tế và sản xuất các thiết bị quan 
trắc cảnh báo phóng xạ môi trường. Kết quả thu được từ hệ số chuyển đổi thông 
lượng sang liều bức xạ và ma trận phản hồi cùng với việc ghi nhận phổ gamma 
đồng vị liên tục từ detector CdZnTe sẽ tạo nên thiết bị quan trắc phóng xạ môi 
trường trực tuyến (online) tin cậy. 
Kỹ thuật điện tử 
Đ. T. Hùng, P. H. Anh, C. V. Hiệp, “Tính toán mô phỏng detector  Monte Carlo.” 156 
TÀI LIỆU THAM KHẢO 
[1]. Kromek Group plc, “Cadmium zinc telluride: room temperature 
semiconductor”, NETPark, County Durham, TS21 3FD, United Kingdom. 
[2]. Knoll, G.F. “Radiation Detection and Measurement” (3rd ed.). Wiley 
(1999). p365 
[3]. Venkataraman, R. “Semiconductor detectors. Handbook of Radioactivity 
Analysis”, Wiley (2020), pp. 409–491. 
[4]. Akkurt, I., Gunoglu, K., & Arda, S. S.”Detection Efficiency of NaI(Tl) 
Detector in 511–1332 keV Energy Range”. Science and Technology of 
Nuclear Installations, 2014, pp. 1–5. 
[5]. López, M., Hofer, H., & Kück, S. “Detection efficiency calibration of single-
photon silicon avalanche photodiodes traceable using double attenuator 
technique”. Journal of Modern Optics, 62(20) (2015), pp. 1732–1738. 
[6]. Zhu, C.-X & Chen, Y. & Guo, H.-P & Mou, Y.-F & An, L. & Wang, X.-H.. 
“The detecting efficiency of HPGe detector”. (2006) 26. pp. 191-194. 
[7]. Baas, H. W., Bode, P., & Blaauw, M. “Ge detector efficiency calculations for 
determination of three-dimensional radioactivity distributions”. Radiation 
Physics and Chemistry, 61(3-6) (2011), pp.637–638. 
[8]. Akkurt, İskender & Tekin, Huseyin Ozan & Mesbahi, Asghar. (2015). 
“Calculation of Detection Efficiency for the Gamma Detector using 
MCNPX”. Acta Physica Polonica A. vol.12 (2015) pp.128-135. 
[9]. Azbouche, A., Belgaid, M., & Mazrou, H. “Monte Carlo calculations of the 
HPGe detector efficiency for radioactivity measurement of large volume 
environmental samples”. Journal of Environmental Radioactivity, 146 (2015), 
pp. 119–124 
[10]. Huy, N. Q., Binh, D. Q., & An, V. X.. “A study for improving detection 
efficiency of an HPGe detector based gamma spectrometer using Monte 
Carlo simulation and genetic algorithms”. Applied Radiation and Isotopes, 
70(12) (2012), pp.2695–2702 
[11]. Reuven Y. Rubinstein, Dirk P. Kroese “Simulation and the Monte Carlo 
Method” (3rd ed). (2016) Wiley. 
[12]. Los Alamos Scientific Laboratory. Group X-6“MCNP : a general Monte 
Carlo code for neutron and photon transport.”, Los Alamos, N.M.:Dept. of 
Energy, Los Alamos Scientific Laboratory (1979). 
[13]. P. F. Rose, Compiler and Editor, “ENDF-201, ENDF/B-VI Summary 
Documentation,” BNL-NCS-17541, Brookhaven National Laboratory 
(October 1991). 
[14]. S. C. Frankle, R. C. Reedy, and P. G. Young, “ACTI An MCNP Data Library 
for Prompt Gamma-ray Spectroscopy,” 12th Biennial Radiation Protection 
and Shielding Topical, Meeting, Santa Fe, NM, April 15-19, 2002. 
[15]. R. J. Howerton, D. E. Cullen, R. C. Haight, M. H. MacGregor, S. T. Perkins, 
and E. F. Plechaty, “The LLL Evaluated Nuclear Data Library (ENDL): 
Evaluation Techniques, Reaction Index, and Descriptions of Individual 
Reactions,” Lawrence Livermore National Laboratory report UCRL-50400, 
Vol. 15, Part A (September 1975). 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 157 
[16]. D. E. Cullen, M. H. Chen, J. H. Hubbell, S. T. Perkins, E. F. Plechaty, J. A. 
Rathkopf, and J. H. Scofield, "Tables and Graphs of Photon Interaction Cross 
Sections from 10 eV to 100 GeV Derived from the LLNL Evaluated Photon 
Data Library (EPDL)," Lawrence Livermore National Laboratory report 
UCRL-50400, Volume 6, Rev. 4, Part A: Z = 1 to 50 and Part B: Z = 51 to 
100 (1989). 
[17]. M. A. Gardner and R. J. Howerton, “ACTL: Evaluated Neutron Activation 
Cross–Section Library-Evaluation Techniques and Reaction Index,” 
Lawrence Livermore National Laboratory report UCRL-50400, Vol. 18 
(October 1978). 
[18]. ICRP Publication 103, The 2007 Recommendations of the International 
Commission on Radiological Protection, International Commission on 
Radiological Protection 
[19]. G. Portal, W. G. Cross, G. Dietze, J. R. Harvey, R. B. Schwartz Report 47 - 
Journal of the International Commission on Radiation Units and 
Measurements, Volume os24, Issue 2, 15 April 1992, Page NP, 
ABSTRACT 
INVESTIGATING IN SIMULATING CdZnTe(CZT) DETECTOR 
BY MONTE CARLO METHOD 
In this paper, the simulating model and the results of the simulation 
obtained from utilizing Monte Carlo method in the study of gamma spectra 
simulation, efficiency, response matrix for semiconductor detector CdZnTe 
(CZT)-1500cm
3
 equipped on UAV radiation reconnaissance flight is 
presented. The simulation results were compared with the experimental 
results for three radioactive sources 
137
Cs, 
60
Co and 
152
Eu. The comparison 
shows that the gamma spectrum, the detector's absolute efficiency are well in 
line with experimental results. The CdZnTe detector model in this study was 
applied to evaluate the efficiency curve and calculate the ambient dose 
equivalent based on the obtained gamma spectrum. 
Keywords: Unmanned aerial vehicle; CdZnTe semiconductor detector; Monte Carlo method; Response 
matrix; Ambient gamma dose rate. 
Nhận bài ngày 20 tháng 3 năm 2020 
Hoàn thiện ngày 21 tháng 8 năm 2020 
Chấp nhận đăng ngày 28 tháng 8 năm 2020 
Địa chỉ: 1Viện Hóa học Môi trường quân sự/Binh chủng Hóa học; 
2Viện Điện tử/Viện Khoa học và Công nghệ quân sự. 
*Email: dinhtienhungnbc@gmail.com.