Simulating 3r robot dynamics using imported cad in maplesim

Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 401 
Simulating 3r robot dynamics using imported cad in Maplesim 
by Nguyen Van Tan (Thu Dau Mot University) 
Article Info: Received 20 Oct 2020, Accepted 25 Nov 2020, Available online 15 Dec, 2020 
 Corresponding author: tannv@tdmu.edu.vn 
 https://doi.org/10.37550/tdmu.EJS/2020.04.084 
ABSTRACT 
With the development of information technology, many applications of robots are 
increasingly being applied to support research, learning, and teaching. This 
paper mainly investigates the modeling and simulation of a robotic arm with 3 
degrees of freedom (dofs) for different applications. First, Kinematics and 
dynamics model of the robot based on the standard Denavit Hartenberg (D-H) 
modeling method, where the forward kinematics of robot is analyzed and 
computed to obtain by using the inverse kinematics, and then the solution of the 
robot dynamics is derived. Second, a CAD model of the robot is designed on 
CATIA software to convert to MapleSim software to simulation and control. 
Final, numerical simulation is presented to display results. This work provides a 
potential basis for the realization of the robotic arm in the industrial, education, 
and research field, which is of great significance for improving manufacturing 
efficiency and support teaching and research in the robot field. 
Keywords: Inverse kinematics, Forward Kinematics, MapleSim, Robot arm 
1. Introduction 
With the development of information and mechanical technologies, robots have been 
invented and applied to the manufacturing process, which can improve the production 
efficiency, enhance productivity, improve the working conditions and accelerate the 
industrial automation [1-2]. Several other applications of robot arms were used in the 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 402 
automotive industry and are often used for welding, painting, loading, and unloading [3] 
as well as in the medical field [4, 5]. The robotic arm extends and expands the functions 
of the hand, foot, and brain. It can replace people's work in harsh environments such as 
danger, harmfulness, toxic, low temperature, and high heat: instead of people doing 
heavy and monotonous repetitive work, which can improve labour productivity and 
ensure product quality. Its application has been extended to the field of space 
exploration, deep-sea development, nuclear science research and medical welfare. A 
robot arm is a new technology emerging in the field of modern automatic control and 
has become an important part of modern industrial systems [6]. The robot arm consists 
of the robot arm, controller, servo drive system, detection and sensing components. It is 
a type of automated production equipment with features such as human-like operation, 
automatic control, reprogrammable, and can complete various operations in three-
dimensional space. 
To support robot research, learning, and research, many applications software support 
the design, calculation, analysis, simulation, and optimization of the robot control 
process has been rapidly developing in it. Some software is used a lot such as 
Simmechanics to simulation robot arm which was shown in [7, 8], and MSC Adams to 
analysis and simulation robot arm that was also shown in [9, 10], then, MapleSim has 
used analysis, dynamics simulation and optimization shown in [11-13]. Particularly, 
with LMS AmeSim, Simcenter, and MSC Adams, the simulation results are treated as 
real results that can be accepted in [14, 15]. 
Figure 1. The robot arm model 3R 
In this paper, An application study of the Maplesim software to control and simulate a 
3R robot arm. First, the robot arm model is built in CAD software such as Solidwork or 
Inventor, or Catia that is shown in Figure 1. From this, this model is imported to 
MapleSim. And then, establish constraints, the relationships of robot arm components 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 403 
as well as DC motor actuators to control the robot arm. Here, PID controllers are also 
utilized in the control process. 
2. Denavit and Hartenbergh Representation 
The kinematic equations use matrix algebra to build constrain functions between the 
joint variables and the world coordinate location of the end-effector (position and 
orientation) based on the spatial configuration of a particular robot arm. A systematic 
and generalized approach to represent the kinematic equations of a serial link robot arm 
was proposed by Denavit & Hartenbergh (D-H). 
The notation will be explained on a sample robot arm which is illustrated in figure 2. 
The robot system has three degrees of freedom, based on the transformation matrix Ai (i 
= 1, 2,3) described by the D-H notation, we can get the pose of the robot's end-effector 
only given the individual joint variables and the rod length parameters of the robot [7]. 
Figure 2. Coordinate system of robot Figure 3. Structure kinematic parameters 
for the general link i
th
The homogenous coordinate transformation matrix 1
i
iT can be written as 
1
0
0 0 0 1
i i i i i i
i i i i i i
i i
i
ii
i
i
C S C S S a C
S C C S C a S
T
S C d
   
   
 (1.1) 
where 
cos ; sin ; cos ; sin
i i i ii i i i
C S C S    
and ai, di, αi,i are the geometric parameters of the relative ith joint as shown in Fig 3. 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 404 
They can be defined as: 
αi is the angle between zi-1 and zi about xi 
di is the distance between origin oi-1 and the intersection of the zi-1 axis with the xi 
axis along zi-1 
θi is the angle between xi-1 and xi about zi-1. 
ai is the distance between origin Oi and the intersection of the zi-1 axis with the xi 
axis along xi 
If a position vector Pi is given in the i
th
 coordinate frame, then it can be expressed in the 
(i-1)
th
 coordinate system as the vector Pi-1 by 
 1 1
i
i i ip T p (1.2) 
The homogenous transformation matrix from the n
th 
coordinate frame to the base 
coordinate frame can be determined by multiplying 1
i
iT (i = 1, 2,, n) together in 
sequence, such as 
1 2
0 0 1 1...
n n
nT T T T (1.3) 
Therefore, a position vector pn of the n
th
 coordinate frame can be determined for the 
base coordinate system as: 
1
0 0
o n
np T p
 (1.4) 
Using the D-H procedure, the coordinate frames are defined and the structural 
geometric parameters of the three-link robot arm are presented in Table 1. 
TABLE 1. Joint-Link Parameters for 3R Robot arm 
Link ai i di i 
1 0 90
0 
d1 1 
2 a2 0 0 2 
3 a3 0 0 3 
Therefore, the coordinate transformation matrices 1
i
iT (i = 1, 2, 3) relating the 
coordinates of the i
th
 frame to those of the (i-1)
th
 frame can be written using equation 
(1.1) as follows 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 405 
1
11
0
0 0
0 0
0 1 0
0 0 0 1
i
i
i
C S
S C
T
d
 
 
 (1.5) 
2 2 2
2 2 2
2
22
1
0
0
0 0 1 0
0 0 0 1
C S a C
S C a S
T
  
  
 (1.6) 
0
3
3 3 3
3 0
3
3 3 32
0 0 1 0
0 0 0 1
C S a C
S C a S
T
  
  
 (1.7) 
The homogenous transformation matrix 3 0T from the coordinate frame attached to the 
end-effector to the base coordinate frame can be represented as 
1 23 1 23 1 1 23 2
1 23 1 23 1 1 23 2
23 23 23 2
3 1 2 3
0 0 1 2
3 2
3 2
3 2 10
0 0 0 1
T T T T
C C C S S C a C a C
S C S S C S a C a C
S C a S a S d
       
       
   
 (1.8) 
Where 
23 232 3 2 3
cos( ); sin( );C S     
Based on this transformation matrix, the forward kinematics can determine a precise 
coordinates of the robot arm in the workspace according to the value of each joint angle 
variable. 
The geometric approach is applied to find the inverse kinematics of the three-link robot 
arm shown in Fig 4. A point P representing a given position of the end-effector, which 
is the origin of the last coordinate frame concerning the base coordinate system, can be 
expressed by 
T
x y zp p p p (1.9) 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 406 
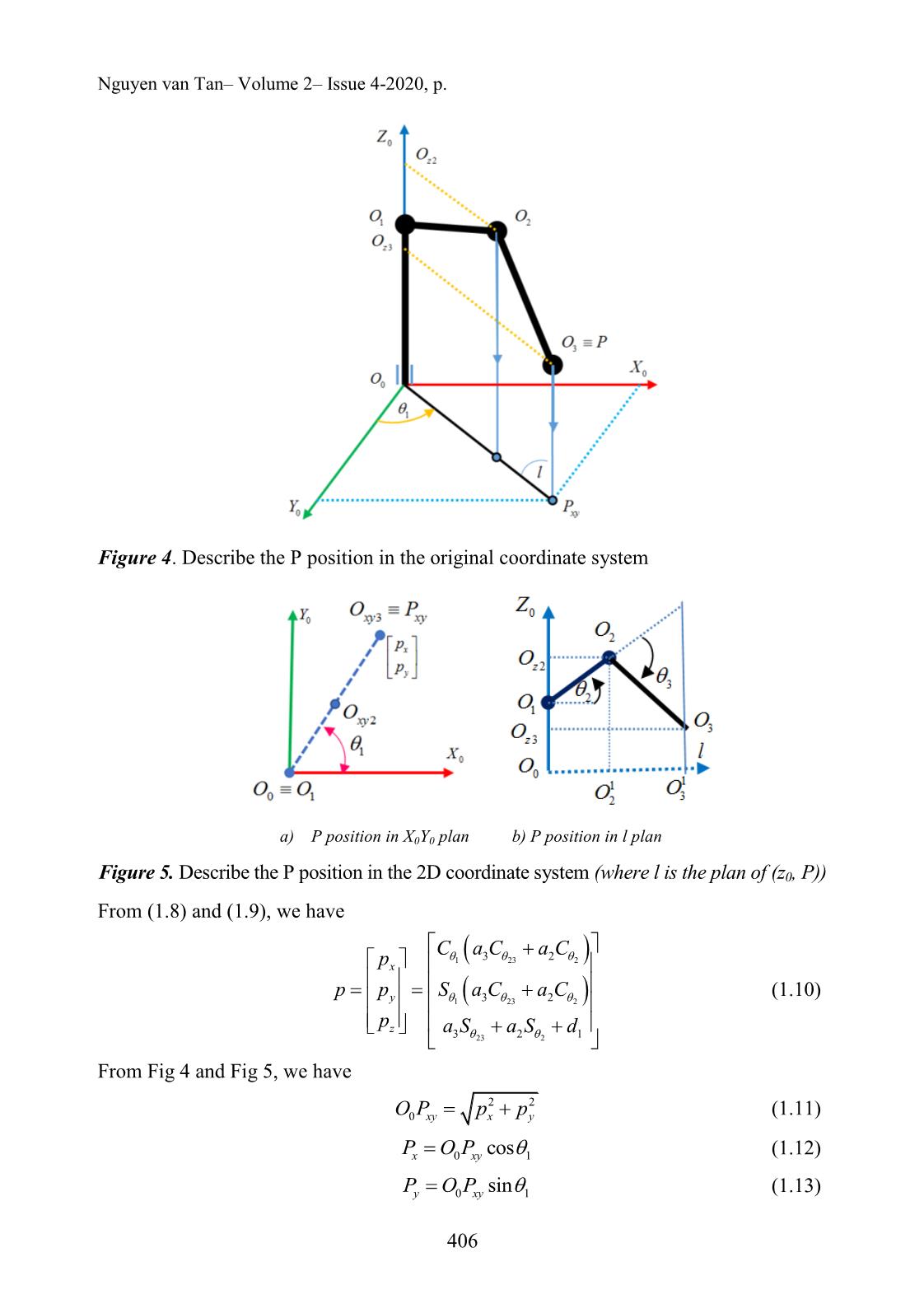
Figure 4. Describe the P position in the original coordinate system 
a) P position in X0Y0 plan b) P position in l plan 
Figure 5. Describe the P position in the 2D coordinate system (where l is the plan of (z0, P)) 
From (1.8) and (1.9), we have 
1 23 2
1 23 2
23 2
3 2
3 2
3 2 1
x
y
z
C a C a C
p
p p S a C a C
p a S a S d
  
  
 
 (1.10) 
From Fig 4 and Fig 5, we have 
 2 20 xy x yO P p p (1.11) 
 0 1cosx xyP O P  (1.12) 
 0 1siny xyP O P  (1.13) 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 407 
Therefore, 1 variable can be calculated as 
 11 tan
y
x
p
p
 
 (1.14) 
Moreover, in Fig. 5. We have 
 1 1 1 10 3 0 2 2 3 2 2 3 2 3cos cosO O O O O O a a   (1.15) 
0 3 0 1 1 2 1 3
1 2 2 3 2 3sin sin
z z zO O O O O O O O
d a a  
 (1.16) 
where 
 1 2 2
0 3 0 0 3;xy x y z zO O O P p p O O p 
Solve equations (1.15) and (1.16) we have 
22 2 2 2
1 2 3
3
2 3
cos
2
x y zp p p d a a
q
a a

 (1.17) 
2
3sin 1 q (1.18) 
Therefore, θ3 can finally be calculated as 
2
1
3
1
tan
q
q
 
 (1.19) 
and θ2 can be calculated as 
2
1
2 3
1
tan

 

 (1.20) 
where 
2 2
1
1
tan
x y
z
p p
p d
; 
22 2 2 2
1 3 2
22 2
3 12
x y z
x y z
p p p d a a
a p p p d

3. Import Cad Robot Model To MapleSim 
MapleSim software was used for the dynamic analysis of the robot model. The basic pre-
requisites includes geometric correctness and the validity of constraints were done in Catia 
software. The material of the robot parts (as this determines the mass and other basic 
dynamic parameters) is equally significant as observed during reverse engineering (RE). 
Once this is done in CATIA the “Motion Study” itself is capable of exporting these details 
along with the geometric model to MapleSim. Verification of the coherence in inertial 
parameters can be confirmed in both MapleSim and CATIA platforms 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 408 
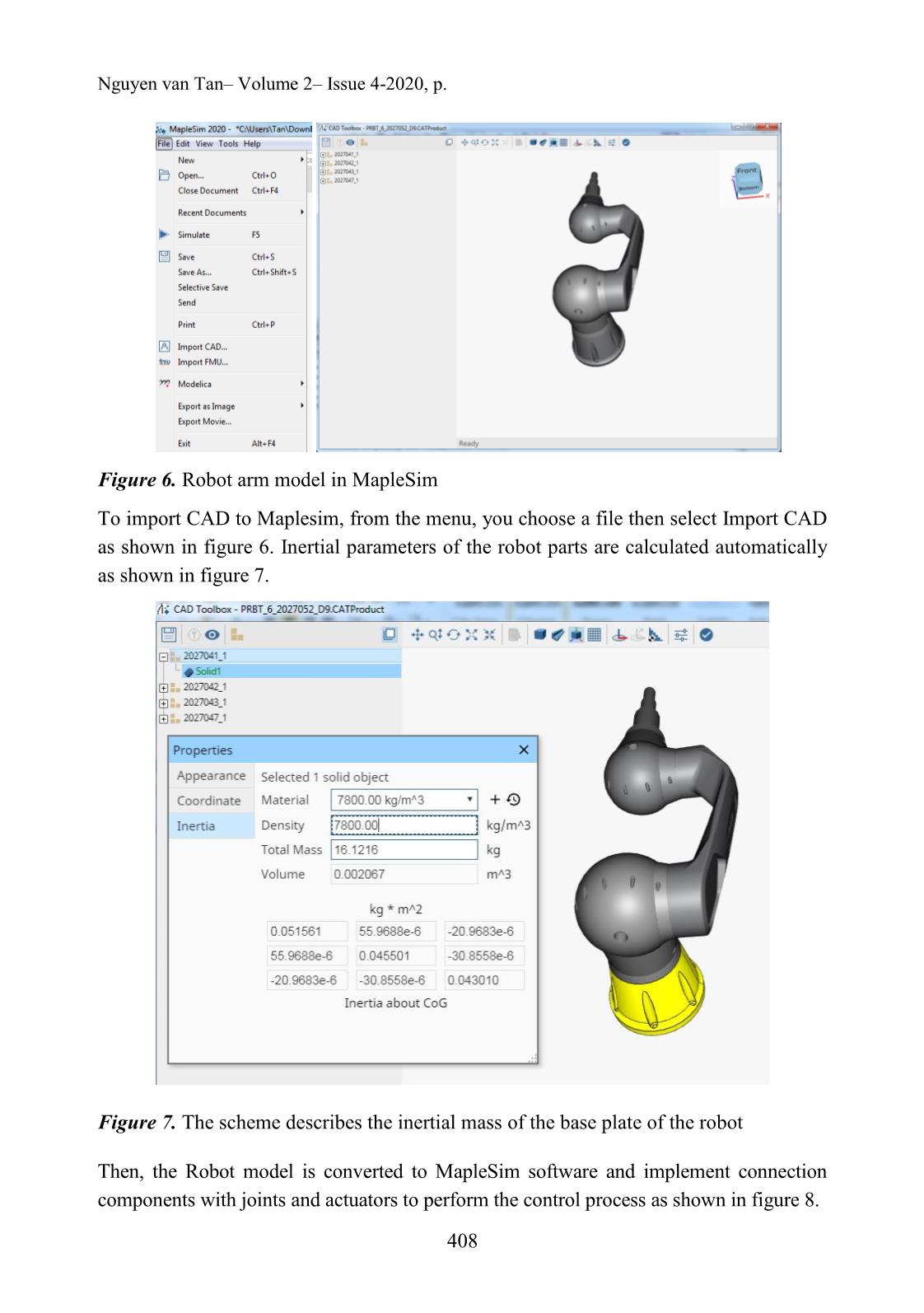
Figure 6. Robot arm model in MapleSim 
To import CAD to Maplesim, from the menu, you choose a file then select Import CAD 
as shown in figure 6. Inertial parameters of the robot parts are calculated automatically 
as shown in figure 7. 
Figure 7. The scheme describes the inertial mass of the base plate of the robot 
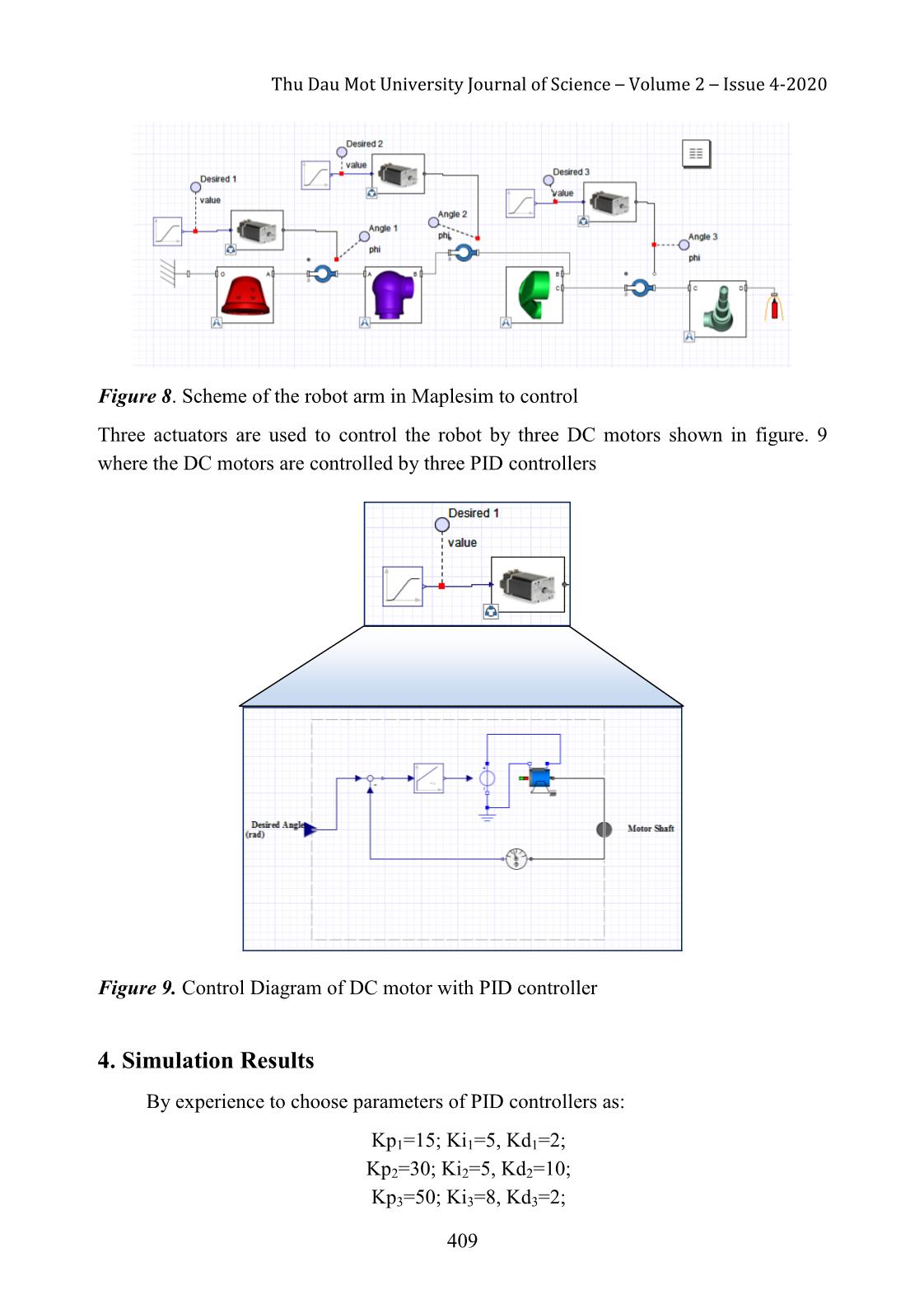
Then, the Robot model is converted to MapleSim software and implement connection 
components with joints and actuators to perform the control process as shown in figure 8. 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 409 
Figure 8. Scheme of the robot arm in Maplesim to control 
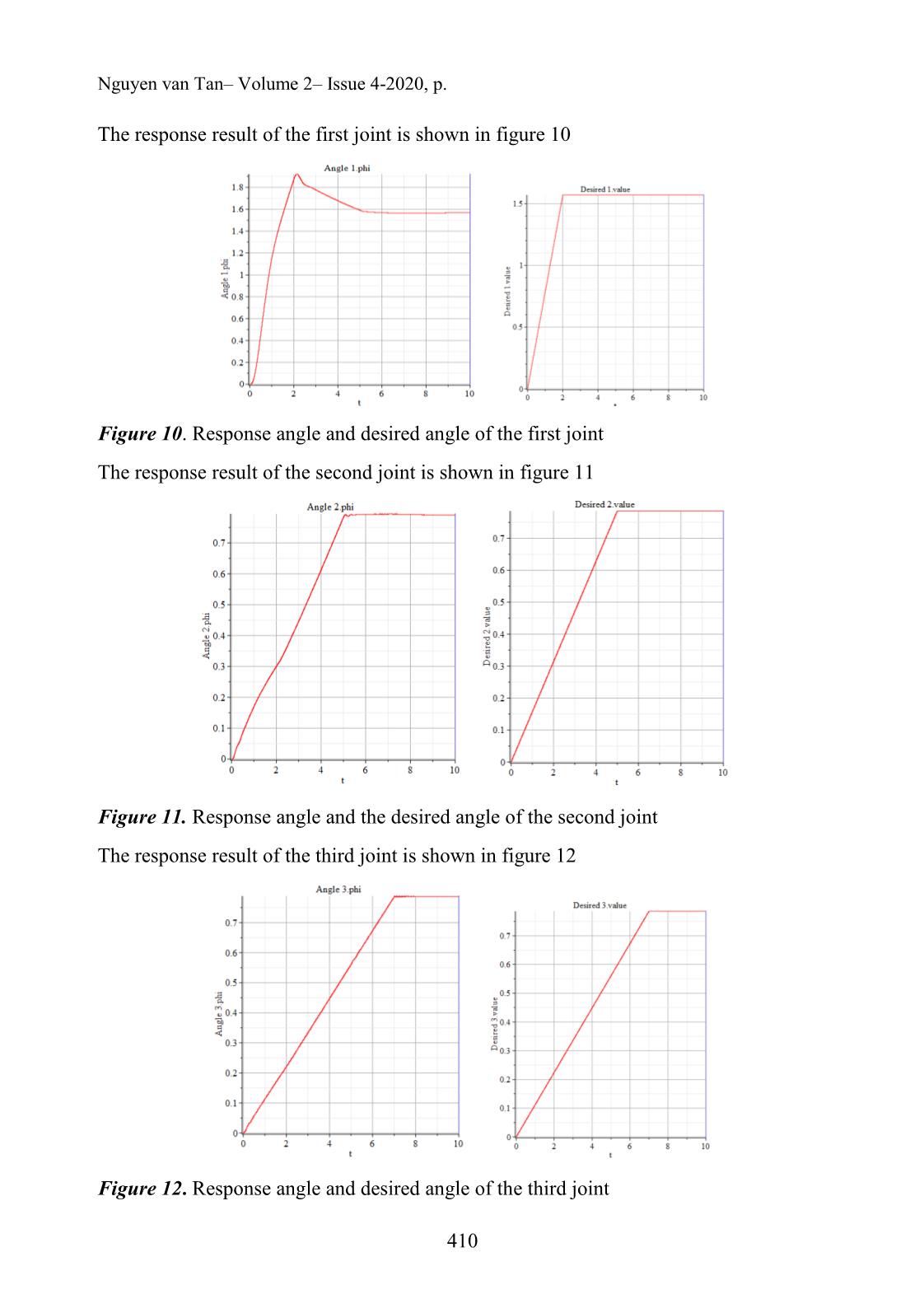
Three actuators are used to control the robot by three DC motors shown in figure. 9 
where the DC motors are controlled by three PID controllers 
Figure 9. Control Diagram of DC motor with PID controller 
4. Simulation Results 
By experience to choose parameters of PID controllers as: 
Kp1=15; Ki1=5, Kd1=2; 
Kp2=30; Ki2=5, Kd2=10; 
Kp3=50; Ki3=8, Kd3=2; 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 410 
The response result of the first joint is shown in figure 10 
Figure 10. Response angle and desired angle of the first joint 
The response result of the second joint is shown in figure 11 
Figure 11. Response angle and the desired angle of the second joint 
The response result of the third joint is shown in figure 12 
Figure 12. Response angle and desired angle of the third joint 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 411 
The simulation result of the robot arm is shown in figure 13. 
3D simulation robot result is stimulated when given three angles of three axes shown in 
figure 10, figure. 11, and figure 12. The trajectory of the end-effector is displayed by the 
red trajectory as shown in figure 13. 
Figure 13. The simulation result of the robot in 3D Maplesim 
5. Conclusion 
The rotation angles of the robot arm joints are calculated based on inverse kinematics of 
the D-H convention. The robot is designed in CATIA to easy converted to Maplesim 
software. The robot arm is set up in maplesim to control and simulation. Simulation 
results were obtained as expected under using PID controller that shown in the figures 
from figure 10 to figure 13. 
Adknowledge: This Research is support by Truong Dai hoc Thu Dau Mot, Binh Duong 
province, Viet Nam 
References 
Nguyen van Tan– Volume 2– Issue 4-2020, p. 
 412 
[1] Y. He et al., (2019). Dynamic Modeling, Simulation, and Experimental Verification of a 
Wafer Handling SCARA Robot With Decoupling Servo Control. IEEE Access, vol. 7, pp. 
47143-47153, doi: 10.1109/ACCESS.2019.2909657. 
[2] Taylan Das M, Canan Dulger L., (2005). Mathematical Modelling, simulation and 
experimental verification of a SCARA Robot. Simulation Modelling Practice and Theory, 
Vol 13, pp. 257-271;. 
[3] W. Jin, et al., (2020). Wire Arc Additive Manufacturing of Stainless Steels: A Review. 
Appl. Sci. , 10(5), 1563; https://doi.org/10.3390/app10051563 
[4] M. Wei, Q. Liu, and , et al., (2015). Recent development of mechanisms and control 
strategies for robot-assisted lower limb rehabilitation. Mechatronics 31, 132-145 
[5] S. S. KAMLESH, A. KUMAR, and et al., (2016). Review on Application of Robot Arm in 
Medical Field with Special Forcus on Image Guided Biopsies. International Journal of 
Mechanical And Production Engineering, 4(11), 
[6] Toz, Met in, and Serdar Kucuk (2010). Dynamics simulation toolbox for industrial robot 
robot arms. Computer Applications in Engineering Education, 18(2), 319-330. 
[7] J. Liu, Q. Luo, (2019). Modeling and Simulation of Robotic Arm in MATLAB for 
Industrial Applications. 11th International Conference on Intelligent Human-Machine 
Systems and Cybernetics (IHMSC), 978-1-7281-1859IEEE 
DOI 10.1109/IHMSC.2019.00086 
[8] J. ZATOPEK, and et al., (2018). Dynamic simulation of the CAD model in SimMechanics 
with multiple uses. Turkish Journal of Electrical Engineering & Computer Sciences, urk J 
Elec Eng & Comp Sci ., 6: 1278 { 1290 
[9] T, Amit., “Forward Kinematic Analysis, Simulation & Workspace Tracing of 
Anthropomorphic Robot Robot arm By Using MSC. ADAMS”. International Journal of 
Innovative Research in Science, Engineering and Technology. 04. Doi: 
10.15680/IJIRSET.2015.0401009. 
[10] Ratiu, Mariana, and et al., (2018). Modeling in ADAMS of a 6R industrial robot. MATEC 
Web of Conferences. Doi: 10.1051/matecconf/201818402006. 
[11] J. Hřebíček, and et al., “Modelling with Maple and MapleSim”. Proceedings 22nd 
European Conference on Modelling and Simulation ©ECMS Loucas S. Louca, Yiorgos 
Chrysanthou, Zuzana Oplatková, Khalid Al-Begain (Editors) ISBN: 978-0-9553018-5-8 / 
ISBN: 978-0-9553018-6-5 (CD) 
[12] D. Wright and O. Soroka (2012). Modeling and simulation of a linear piezoelectric stepper 
motor in maplesim. IEEE International Ultrasonics Symposium, Dresden, pp. 2746-2749, 
doi: 10.1109/ULTSYM.2012.0688. 
[13] Korobkine, A., Boimer, R., Pantelic, V., Shah, S. et al., (2018). Automatic Calibrations 
Generation for Powertrain Controllers Using MapleSim. SAE Technical Paper 
https://doi.org/10.4271/2018-01-1458. 
[14] P, Aron, and et al., (2015). Real-time co-simulation platform for electromechanical vehicle 
applications). 9th International Symposium on Advanced Topics in Electrical Engineering, 
ATEE (2015). 240-243. Doi:10.1109/ATEE.2015.7133772. 
[15] X. Feixiang and et al., (2018). Modeling and co-simulation based on Adams and AMESim 
of pivot steering system. The Journal of Engineering. Doi: 10.1049/joe.2018.9018. 
Thu Dau Mot University Journal of Science – Volume 2 – Issue 4-2020 
 413