Phương pháp điều khiển thích nghi không có mô hình cho rô bốt dây song song

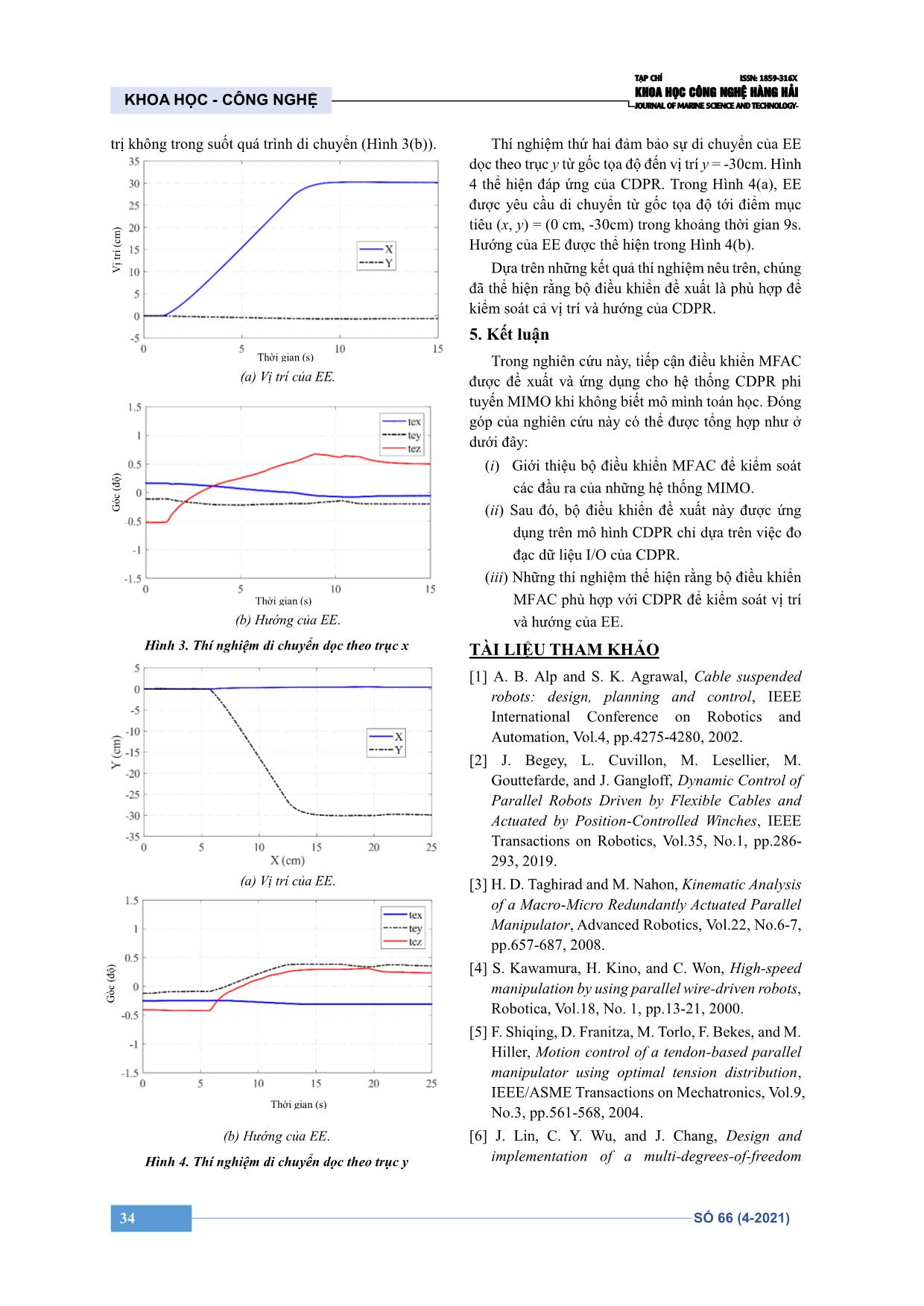
KHOA HỌC - CÔNG NGHỆ 
TẠP CHÍ ISSN: 1859-316X 
KHOA HỌC CÔNG NGHỆ HÀNG HẢI 
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY 
31 SỐ 66 (4-2021) 
PHƯƠNG PHÁP ĐIỀU KHIỂN THÍCH NGHI KHÔNG CÓ MÔ HÌNH CHO 
RÔ BỐT DÂY SONG SONG 
MODEL-FREE ADAPTIVE CONTROL APPROACH FOR CABLE-DRIVEN 
PARALLEL ROBOT 
PHẠM ĐÌNH BÁ1*, PHẠM XUÂN DƯƠNG2 
1Viện Cơ khí, Trường Đại học Hàng hải Việt Nam 
2Trường Đại học Hàng hải Việt Nam 
*Email liên hệ: bapd.vck@vimaru.edu.vn 
Tóm tắt 
Khi mô hình toán học không có sẵn và các điều 
kiện cụ thể của hệ thống được cung cấp, phương 
pháp điều khiển thích nghi không có mô hình 
(MFAC) được đề xuất dựa trên kỹ thuật tuyến tính 
hóa động với đạo hàm riêng cho hệ thống rời rạc 
nhiều đầu vào và nhiều đầu ra. Ý tưởng điều khiển 
chính là thiết lập các thông số hệ thống thời gian 
thực đại diện cho các biến của hệ thống được thực 
hiện bằng cách chỉ sử dụng các đầu vào và đầu 
ra. Sau đó, bộ điều khiển đề xuất được thực hiện 
thành công cho một robot song song điều khiển 
bằng dây (CDPR) để điều khiển vị trí của robot 
(EE). MFAC này đã được áp dụng và chứng minh 
hiệu suất đạt yêu cầu trên nền tảng CDPR thực tế. 
Từ khóa: Điều khiển không mô hình, điều khiển 
thích nghi, robot song song. 
Abstract 
When a mathematical model is not available and 
system-specific conditions are fulfilled, a model-
free adaptive control (MFAC) approach is 
proposed based on a new dynamic linearization 
technique with a pseudo-partial derivative for a 
class of general multiple-input and multiple-
output nonlinear discrete-time cable robot system. 
The key control ideal is that an estimation of real-
time system parameters that represent system 
dynamic variations is realized by using only 
inputs and outputs. Then the proposed controller 
is successfully implemented in a cable-driven 
parallel robot (CDPR) to control the position of 
the end-effector (EE). This MFAC was applied 
and demonstrated satisfactory performance on an 
actual CDPR platform. 
Keywords: Model-free control, adaptive control, 
parallel robot. 
1. Giới thiệu chung 
CDPRs là một robot mà chuyển vị (bao gồm vị trí 
và hướng) của EE được điều chỉnh bởi các dây độc lập 
với một đầu nối với EE và đầu còn lại nối với khung 
[1, 2]. EE được điều khiển đến vị trí và hướng mong 
muốn bằng việc thay đổi chiều dài của các dây. Những 
ưu điểm chính của CDPRs bao gồm không gian làm 
việc lớn [3], tốc độ cao [4, 5], và có khả năng chịu tải 
lớn [6]. 
Gần đây, các thuật toán điều khiển cho CDPR đã 
gây được sự chú ý đáng kể. Luật điều khiển phản hồi 
PD [4] và PID [7] trong không gian khớp được khai 
thác để kiểm soát chuyển vị của EE. Một bộ điều 
khiển bền vững PID [8] được thiết kế cho CDPR với 
sự không chắc chắn về cấu trúc của hệ thống. Phương 
pháp điều khiển phân cấp [6] được phát triển để đáp 
ứng điều khiển vị trí. Một bộ điều khiển mô men xoắn 
tính toán (CTC) [5] được đề xuất cho một robot song 
song. Hệ thống điều khiển tạo thành một phần chuyển 
tiếp động nghịch đảo và một vòng phản hồi. Một tiếp 
cận điều khiển trong [2] dựa trên CTC với hồi tiếp 
tuyến tính được giới thiệu để điều khiển CDPR với 
những dây có tính đàn hồi lớn. Một bộ điều khiển 
đồng bộ hóa [9] được sử dụng để nhận ra chuyển động 
đồng bộ hóa giữa các dây và vị trí điều khiển chính 
xác của EE. Các kế hoạch điều khiển khác cũng đã 
được áp dụng cho CDPR, chẳng hạn như bộ điều 
khiển trượt (SMC) [10-12], SMC giảm [13], hoặc điều 
khiển thụ động [14]. Hơn nữa, bộ điều khiển mạng 
noron thích nghi [15] cũng được sử dụng cho CDPR 
với độ bão hòa đầu vào để bù lại sự không chính xác 
của mô hình hệ thống. 
Điều khiển thích nghi không mô hình lần đầu tiên 
được giới thiệu bởi Hou [16, 17] cho các hệ thống phi 
tuyến rời rạc. Thuật toán điều khiển này được sử dụng 
rộng rãi trong nhiều lĩnh vực. Dựa trên lý thuyết 
MFAC, vấn đề kiểm soát hướng đi của các thiết bị mặt 
nước [18] với sự không chắc chắn được điều tra. Một 
thuật toán MFAC mới [19] dựa trên phương pháp 
chiếu kép liên tiếp được đề xuất cho các bài toán điều 
khiển xe ô tô tự lái. Yaoyao [20] phát triển một 
KHOA HỌC - CÔNG NGHỆ 
32 SỐ 66 (4-2021) 
TẠP CHÍ ISSN: 1859-316X 
KHOA HỌC CÔNG NGHỆ HÀNG HẢI 
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY 
phương pháp điều khiển bền vững không mô hình dựa 
trên phương pháp điều khiển trượt và phương pháp 
điều khiển không mô hình cho robot song song. Raul-
Cristian [21] kết hợp MFAC với thành phần mờ bằng 
cách điều chỉnh phản hồi tham chiếu ảo cho các hệ 
thống cần cẩu tháp. Kết quả thuật toán được minh 
chứng thông qua vị trí góc cánh tay robot của cần cẩu 
tháp trang bị trong phòng thí nghiệm. 
Trong nghiên cứu này, điều khiển không mô hình 
(MFAC) được thiết kế dựa trên những lý thuyết được 
trình bày trong [17, 18, 22] để điều khiển vị trí của 
CDPR. Bộ điều khiển đề xuất là dựa trên mô hình 
động lực học tuyến tính và đạo hàm riêng của hệ thống 
rời rạc phi tuyến nhiều tín hiệu vào nhiều tín hiệu ra 
(MIMO). 
2. Vấn đề về điều khiển không mô hình 
Mô hình đầu vào/đầu ra (I/O) của một hệ thống rời 
rạc phi tuyến MIMO [17] được mô tả như sau 
 1 , , , ,y uk k k n k k n y f y y u u , (1) 
Trong đó: pk y và qk u tương ứng là 
các I/O, nv, nu là bậc tự do, p, q là các số nguyên, và 
 p f là hàm phi tuyến. 
Dạng tuyến tính động của hệ thống rời rạc (1) 
được xây dựng dựa trên các giả thiết sau: 
Giả thiết 1: Đạo hàm từng phần của f đối với 
đầu vào ku là liên tục. 
Giả thiết 2: 1k b k y u và 0k u 
cho mỗi k, với 1 1k k k y y y , 
 1k k k u u u , và b là một hằng số dương. 
Như thảo luận trong [17], hệ thống phi tuyến rời 
rạc (1) có thể chuyển đổi thành một mô hình dữ liệu 
 1k k k y Φ u , (2) 
Trong đó: kΦ là ma trận giả Jacobi (PJM), 
11 12 1
11 12 1
11 12 1
q
q
q p q
k k k
k k k
k
k k k
   
   
   
Φ 
và k b Φ . 
3. Thiết kế bộ điều khiển MFAC 
Trong nghiên cứu này, mục tiêu chính là điều 
khiển hệ thống MIMO khi không biết mô hình toán 
trong điều kiện cụ thể, chỉ sử dụng dữ liệu đo đạc I/O 
của hệ thống điều khiển vòng kín. Quan tâm đến hàm 
tối ưu sau: 
2 2
1 1 1dJ k k k k y y u u , (3) 
Trong đó: 1d k y là tín hiệu ra mong muốn và 
 là một hằng trọng số. 
Từ (2), công thức có thể được viết lại như sau: 
 1 1k k k k k y y Φ u u . (4) 
Thế (4) vào (3) chúng ta có 
2
2
1 1
1
d
u
k k k k k
J
k k
y y Φ u u
u u
. (5) 
Khi hệ thống ổn định, hàm tối ưu Ju tiến tới không. 
Do vậy, đạo hàm của (5) theo u(k), và cho nó bằng 
không, Ju tiếp cận tới giá trị tối ưu xung quanh giá trị 
không. 
 21 1d
k
k k k k
k
Φ
u u y y
Φ
. (6) 
Trong thực tế, Ju có thể không hội tụ. Vấn đề này 
có thể được khắc phục bằng cách đề xuất tham số 
 0 1  để giảm kích thước bước lặp. Sau đó, công 
thức (6) có thể được viết lại như sau: 
 21 1d
k
k k k k
k

Φ
u u y y
Φ
. (7) 
Để thiết lập kΦ , một hàm tối ưu khác đưa ra 
trong [22] cho ˆ kΦ được sử dụng trong nghiên cứu 
này. 
2
2
ˆ 1
ˆ ˆ 1
k k k
J
k k

y Φ u
Φ Φ
, (8) 
Trong đó: 0 là trọng số. 
Hình 1. Sơ đồ điều khiển của MFAC [17] 
KHOA HỌC - CÔNG NGHỆ 
33 SỐ 66 (4-2021) 
TẠP CHÍ ISSN: 1859-316X 
KHOA HỌC CÔNG NGHỆ HÀNG HẢI 
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY 
Khi cho / 0J k  Φ , chúng ta thu được: 
2
2
ˆ 1
1
ˆ
1
1
1
T
k
k
k
k k
k



Φ
u
Φ
y u
u
. (9) 
Để đảm bảo tính hội tụ của ˆ kΦ , thông số 
 0 1  được đề xuất để giảm kích thước bước lặp. 
2
2
ˆ 1
1
ˆ
1
1
T
k
k
k
k k
k




Φ
u
Φ
y u
u
 , (10) 
với ˆ 1Φ là giá trị khởi tạo của PJM. 
PJM [18] khởi động lại khi: 
ˆ
ˆ ˆ 1 if 1
ˆ ˆ 1
k
k k
sign k sign


Φ
Φ Φ u
Φ Φ
, (11) 
Trong đó: sign là hàm sign và ε là một số dương 
bé tùy ý. 
Trong kế hoạch điều khiển của MFAC, dữ liệu I/O 
của hệ thống điều khiển được sử dụng để thiết lập 
thông số thay đổi theo thời gian kΦ . Giá trị thiết 
lập ˆ kΦ và tối ưu hóa sai số được giới thiệu trong 
kế hoạch điều khiển, tín hiệu điều khiển mới ku là 
đạt được. Dựa trên tín hiệu điều khiển ku và đầu ra 
 ky , PJM mới được thiết lập thông qua ˆ 1k Φ . 
Toàn bộ quá trình điều khiển được mô tả như trong 
Hình 1. 
4. Nghiên cứu trường hợp cho CDPR 
Trong phần này, các thí nghiệm tập trung vào kiểm 
soát vị trí của EE trong không gian khớp của CDPR. 
CDPR là một hệ thống MIMO trong đó tín hiệu ra 
 1 2 8
T
k l k l k l k y , ở đó li là chiều dài 
của dây thứ i (i = 1  8) và tín hiệu vào 
 1 2 8k k k k   u với i là mô men 
điều khiển của dây thứ i trong không gian khớp. 
Động học ngược [23] được sử dụng để chuyển đổi 
chuyển vị của EE thành chiều dài của các dây: 
i i il a Ξb p , (12) 
Trong đó: 
ia là véc tơ vị trí của đầu dây thứ i nối 
với khung, 
ib là véc tơ vị trí của đầu dây thư i nối 
với EE,  
T
x y z p là véc tơ vị trí của trọng tâm 
của EE, và Ξ là một ma trận chuyển. 
Hình 2. Mô hình CDPR trong phòng thí nghiệm 
c c s s c c s c s c s s
c s s s s c c c s s s c
s s c c c
       
       
  
Ξ , 
Trong đó: , , và  tương ứng là các góc nghiêng 
của EE theo ba trục x, y, và z, cosc  , sins  , 
cosc  , sins  , cosc  , và sins  . 
Mô hình trong phòng thí nghiệm của CDPR được 
thể hiện trong Hình 2. Phần cứng bao gồm máy tính 
HP (Intel® Core™ i-7 CPU 3.4GHz), được sử dụng 
để tính toán tín hiệu điều khiển và điều khiển 08 mô 
tơ (Delta, ECMA-C10604ES) thông qua mạch D/A 
(TEXAS INSTRUMENTS LUANCHXL-F280049C 
and TMS320F28379D). Chiều dài của mỗi dây được 
xác định thông qua các encoder (gắn trên các mô tơ) 
và hồi tiếp thông chuẩn giao tiếp CAN-Bus tới máy 
tính. Phần mềm điều khiển được thực hiện với 
Simulink/Matlab. 
Các thông số của CDPR được sử dụng trong thí 
nghiệm là: m = 1,91kg; g = 9,81m/s2; Ix = 0,059kgm2; 
Iy = 0,59 kgm2; và Iz = 0,002kgm2. 
Điều kiện khởi tạo và các thông số của bộ điều 
khiển là: i(0) = 0, l1(0) = l2(0) = l3(0) = l4(0) = 1,048m; 
l5(0) = l6(0) = l7(0) = l8(0) = 1,08m; ˆ 1Φ = 
diag(0,1;0,1;0,1;0,1;0,1;0,1;0,1;0,1);  = 0,38; = 
0,003;  = 0,095;  = 0,0095; và  = 0,008. 
Thí nghiệm được đưa ra để hoàn thành hai nhiệm 
vụ di chuyển dọc theo trục x và trục y. 
Thí nghiệm đầu tiên điều tra đặc tính di chuyển 
của CDPR dọc theo trục x. Trong thí nghiệm này, EE 
di chuyển từ điểm này (x, y) = (0, 0) tới điểm mục tiêu 
(x, y) = (30cm, 0cm). Đáp ứng điều khiển được thể 
hiện trong Hình 3. Vị trí của EE được mô tả trong 
Hình 3(a), trong khi hướng của EE duy trì quanh giá 
EE 
Dây 
Mô tơ 
Mô tơ driver 
Máy tính HP 
Vi điều khiển 
KHOA HỌC - CÔNG NGHỆ 
34 SỐ 66 (4-2021) 
TẠP CHÍ ISSN: 1859-316X 
KHOA HỌC CÔNG NGHỆ HÀNG HẢI 
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY 
trị không trong suốt quá trình di chuyển (Hình 3(b)). 
(a) Vị trí của EE. 
(b) Hướng của EE. 
Hình 3. Thí nghiệm di chuyển dọc theo trục x 
(a) Vị trí của EE. 
(b) Hướng của EE. 
Hình 4. Thí nghiệm di chuyển dọc theo trục y 
Thí nghiệm thứ hai đảm bảo sự di chuyển của EE 
dọc theo trục y từ gốc tọa độ đến vị trí y = -30cm. Hình 
4 thể hiện đáp ứng của CDPR. Trong Hình 4(a), EE 
được yêu cầu di chuyển từ gốc tọa độ tới điểm mục 
tiêu (x, y) = (0 cm, -30cm) trong khoảng thời gian 9s. 
Hướng của EE được thể hiện trong Hình 4(b). 
Dựa trên những kết quả thí nghiệm nêu trên, chúng 
đã thể hiện rằng bộ điều khiển đề xuất là phù hợp để 
kiểm soát cả vị trí và hướng của CDPR. 
5. Kết luận 
Trong nghiên cứu này, tiếp cận điều khiển MFAC 
được đề xuất và ứng dụng cho hệ thống CDPR phi 
tuyến MIMO khi không biết mô mình toán học. Đóng 
góp của nghiên cứu này có thể được tổng hợp như ở 
dưới đây: 
(i) Giới thiệu bộ điều khiển MFAC để kiểm soát 
các đầu ra của những hệ thống MIMO. 
(ii) Sau đó, bộ điều khiển đề xuất này được ứng 
dụng trên mô hình CDPR chỉ dựa trên việc đo 
đạc dữ liệu I/O của CDPR. 
(iii) Những thí nghiệm thể hiện rằng bộ điều khiển 
MFAC phù hợp với CDPR để kiểm soát vị trí 
và hướng của EE. 
TÀI LIỆU THAM KHẢO 
[1] A. B. Alp and S. K. Agrawal, Cable suspended 
robots: design, planning and control, IEEE 
International Conference on Robotics and 
Automation, Vol.4, pp.4275-4280, 2002. 
[2] J. Begey, L. Cuvillon, M. Lesellier, M. 
Gouttefarde, and J. Gangloff, Dynamic Control of 
Parallel Robots Driven by Flexible Cables and 
Actuated by Position-Controlled Winches, IEEE 
Transactions on Robotics, Vol.35, No.1, pp.286-
293, 2019. 
[3] H. D. Taghirad and M. Nahon, Kinematic Analysis 
of a Macro-Micro Redundantly Actuated Parallel 
Manipulator, Advanced Robotics, Vol.22, No.6-7, 
pp.657-687, 2008. 
[4] S. Kawamura, H. Kino, and C. Won, High-speed 
manipulation by using parallel wire-driven robots, 
Robotica, Vol.18, No. 1, pp.13-21, 2000. 
[5] F. Shiqing, D. Franitza, M. Torlo, F. Bekes, and M. 
Hiller, Motion control of a tendon-based parallel 
manipulator using optimal tension distribution, 
IEEE/ASME Transactions on Mechatronics, Vol.9, 
No.3, pp.561-568, 2004. 
[6] J. Lin, C. Y. Wu, and J. Chang, Design and 
implementation of a multi-degrees-of-freedom 
Thời gian (s) 
V
ị 
tr
í 
(c
m
) 
Thời gian (s) 
G
ó
c 
(đ
ộ
) 
Thời gian (s) 
G
ó
c 
(đ
ộ
) 
KHOA HỌC - CÔNG NGHỆ 
35 SỐ 66 (4-2021) 
TẠP CHÍ ISSN: 1859-316X 
KHOA HỌC CÔNG NGHỆ HÀNG HẢI 
JOURNAL OF MARINE SCIENCE AND TECHNOLOGY 
cable-driven parallel robot with gripper, 
International Journal of Advanced Robotic 
Systems, Vol.15, No.5, 2018. 
[7] D. Wang et al., Winch-integrated mobile end-
effector for a cable-driven parallel robot with 
auto-installation, International Journal of Control, 
Automation and Systems, journal article Vol.15, 
No.5, pp.2355-2363, 2017. 
[8] M. A. Khosravi and H. D. Taghirad, Robust PID 
control of fully-constrained cable driven parallel 
robots, Mechatronics, Vol.24, No.2, pp.87-97, 
2014. 
[9] W. Shang, B. Zhang, B. Zhang, F. Zhang, and S. 
Cong, Synchronization Control in the Cable Space 
for Cable-Driven Parallel Robots, IEEE 
Transactions on Industrial Electronics, Vol.66, 
No.6, pp.4544-4554, 2019. 
[10] H. Bayani, M. T. Masouleh, and A. Kalhor, An 
experimental study on the vision-based control 
and identification of planar cable-driven parallel 
robots, Robotics and Autonomous Systems, 
Vol.75, pp.187-202, 2016. 
[11] A. Alikhani and M. Vali, Modeling and robust 
control of a new large scale suspended cable-
driven robot under input constraint, 8th 
International Conference on Ubiquitous Robots 
and Ambient Intelligence, pp.238-243, 2011. 
[12] S. A. Khalilpour, R. Khorrambakht, H. D. 
Taghirad, and P. Cardou, Robust cascade control 
of a deployable cable-driven robot, Mechanical 
Systems and Signal Processing, Vol.127, pp.513-
530, 2019. 
[13] M. Zeinali and A. Khajepour, Design and 
Application of Chattering-Free Sliding Mode 
Controller to Cable-Driven Parallel Robot 
Manipulator: Theory and Experiment, 2010. 
[14] R. J. Caverly and J. R. Forbes, Dynamic 
Modeling and Noncollocated Control of a Flexible 
Planar Cable-Driven Manipulator, IEEE 
Transactions on Robotics, Vol.30, No.6, pp.1386-
1397, 2014. 
[15] H. Jabbari Asl and F. Janabi-Sharifi, Adaptive 
neural network control of cable-driven parallel 
robots with input saturation, Engineering 
Applications of Artificial Intelligence, Vol.65, 
pp.252-260, 2017. 
[16] Z. Hou and S. Jin, Model free adaptive control: 
theory and applications, CRC press, 2013. 
[17] Z. Hou and S. Jin, Data-Driven Model-Free 
Adaptive Control for a Class of MIMO Nonlinear 
Discrete-Time Systems, IEEE Transactions on 
Neural Networks, Vol.22, No.12, pp.2173-2188, 
2011. 
[18] Q. Jiang, Y. Li, Y. Liao, Y. Miao, W. Jiang, and 
H. Wu, Information fusion model-free adaptive 
control algorithm and unmanned surface vehicle 
heading control, Applied Ocean Research, Vol.90, 
2019. 
[19] S. Liu, Z. Hou, T. Tian, Z. Deng, and Z. Li, A 
Novel Dual Successive Projection-Based Model-
Free Adaptive Control Method and Application to 
an Autonomous Car, IEEE Transactions on Neural 
Networks and Learning Systems, Vol.30, No.11, 
pp.3444-3457, 2019. 
[20] Y. Wang, S. Meng, F. Ju, B. Chen, and H. Wu, A 
Novel Model-Free Robust Control of Cable-
Driven Manipulators, IEEE Access, Vol.7, pp. 
125532-125541, 2019. 
[21] R.-C. Roman, R.-E. Precup, C.-A. Bojan-Dragos, 
and A.-I. Szedlak-Stinean, Combined Model-Free 
Adaptive Control with Fuzzy Component by 
Virtual Reference Feedback Tuning for Tower 
Crane Systems, Procedia Computer Science, 
Vol.162, pp.267-274, 2019. 
[22] Z. Hou, R. Chi, and H. Gao, An overview of 
dynamic-linearization-based data-driven control 
and applications, IEEE Transactions on Industrial 
Electronics, Vol.64, No.5, pp.4076-4090, 2017. 
[23] A. Ghasemi, M. Eghtesad, and M. Farid, Neural 
Network Solution for Forward Kinematics 
Problem of Cable Robots, Journal of Intelligent & 
Robotic Systems, Vol.60, No.2, pp.201-215, 2010. 
 Ngày nhận bài: 12/12/2020 
Ngày nhận bản sửa: 28/01/2021 
Ngày duyệt đăng: 12/02/2021