Phân tích tĩnh của tấm FGM sử dụng phương pháp Mesh-Free và lý thuyết đơn giản biến dạng cắt bậc nhất
Vật liệu biến đổi chức năng (Functionally Graded Material- FGM) là một loại composite có đặc tính vật liệu biến đổi liên tục trong vật thể do đó sẽ loại bỏ được hiện tượng tập trung ứng suất thường gặp ở loại composite thông thường. FGM thường được chế tạo từ hỗn hợp gồm gốm và kim loại. Đây là loại vật liệu
đẳng hướng nhưng không đồng nhất. Hiện nay, FGM được quan tâm vì có thể tạo ra những kết cấu có khả năng thích ứng với những điều kiện vận hành. Thông thường, phân tích ứng xử của tấm vật liệu chức năng
dựa trên các lý thuyết cơ bản sau: (i) Tấm cổ điển (CP), (ii) Biến dạng cắt bậc nhất (FSD), (iii) Biến dạng cắt bậc cao (HSD). Lý thuyết CP (Kirchhoff G, 1850) không xét đến ảnh hưởng của biến dạng cắt ngang đến ứng xử của tấm mỏng. Khi chiều dày tấm tăng lên, biến dạng cắt ngang có ảnh hưởng đáng kể đến đáp ứng của tấm. Lý thuyết FSD đề xuất bởi Mindlin R. D. (1951) và Reissner E. (1945) xét đến ảnh hưởng biến dạng cắt này bằng cách xây dựng trường chuyển vị tuyến tính bậc nhất trong mặt phẳng dọc theo chiều dày của tấm. Tuy vậy, các phương trình cân bằng, ổn định được xây dựng dựa trên lý thuyết CPT và FSDT đều không thỏa mãn điều kiện biên về sự triệt tiêu ứng suất ở mặt trên và dưới của tấm. Nhằm giải quyết được khó khăn này, một hệ số điều chỉnh biến dạng cắt được sử dụng để điều chỉnh mối quan hệ kết hợp giữa ứng suất cắt và biến dạng cắt ngang.

Trang 1

Trang 2
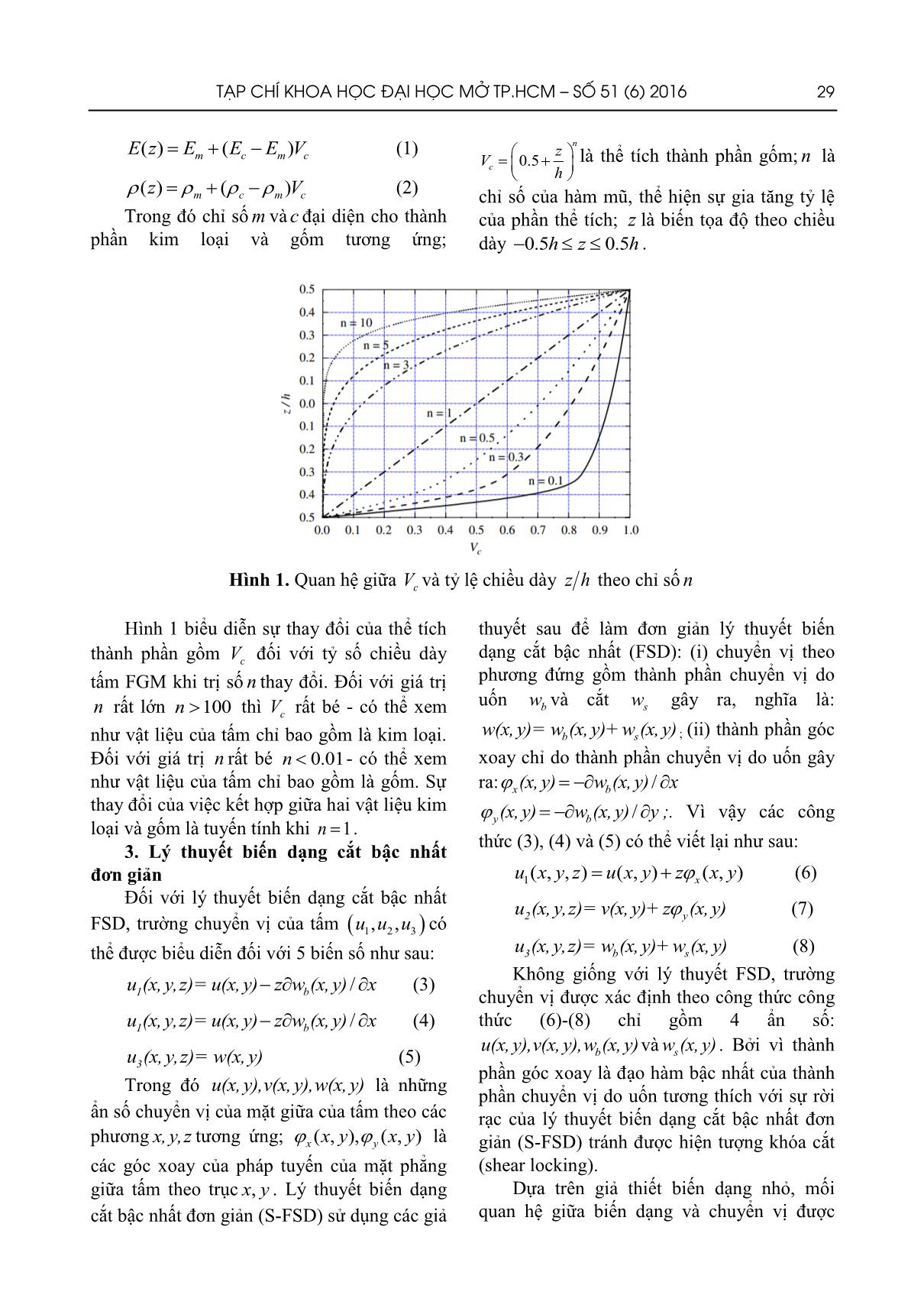
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
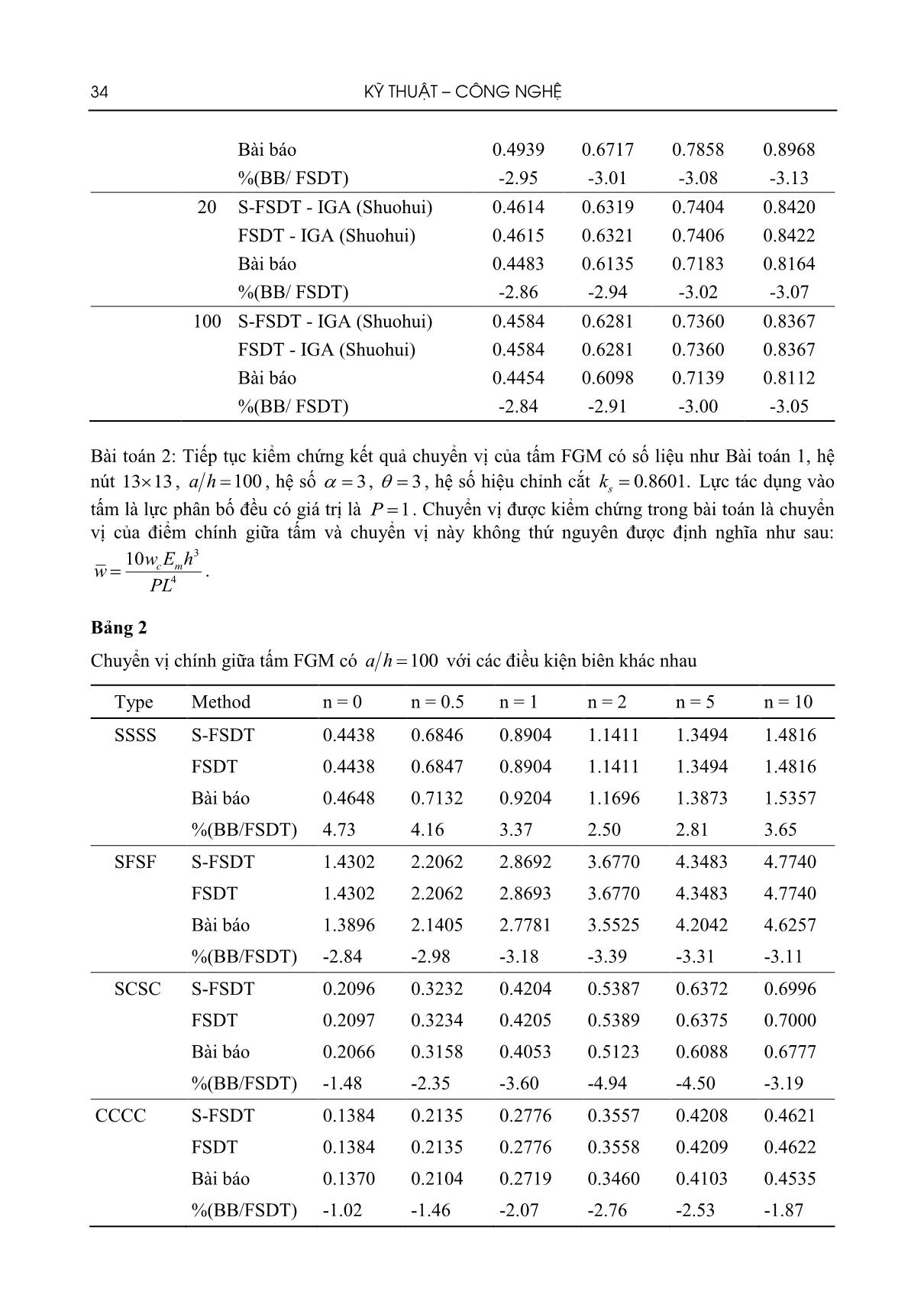
Trang 8
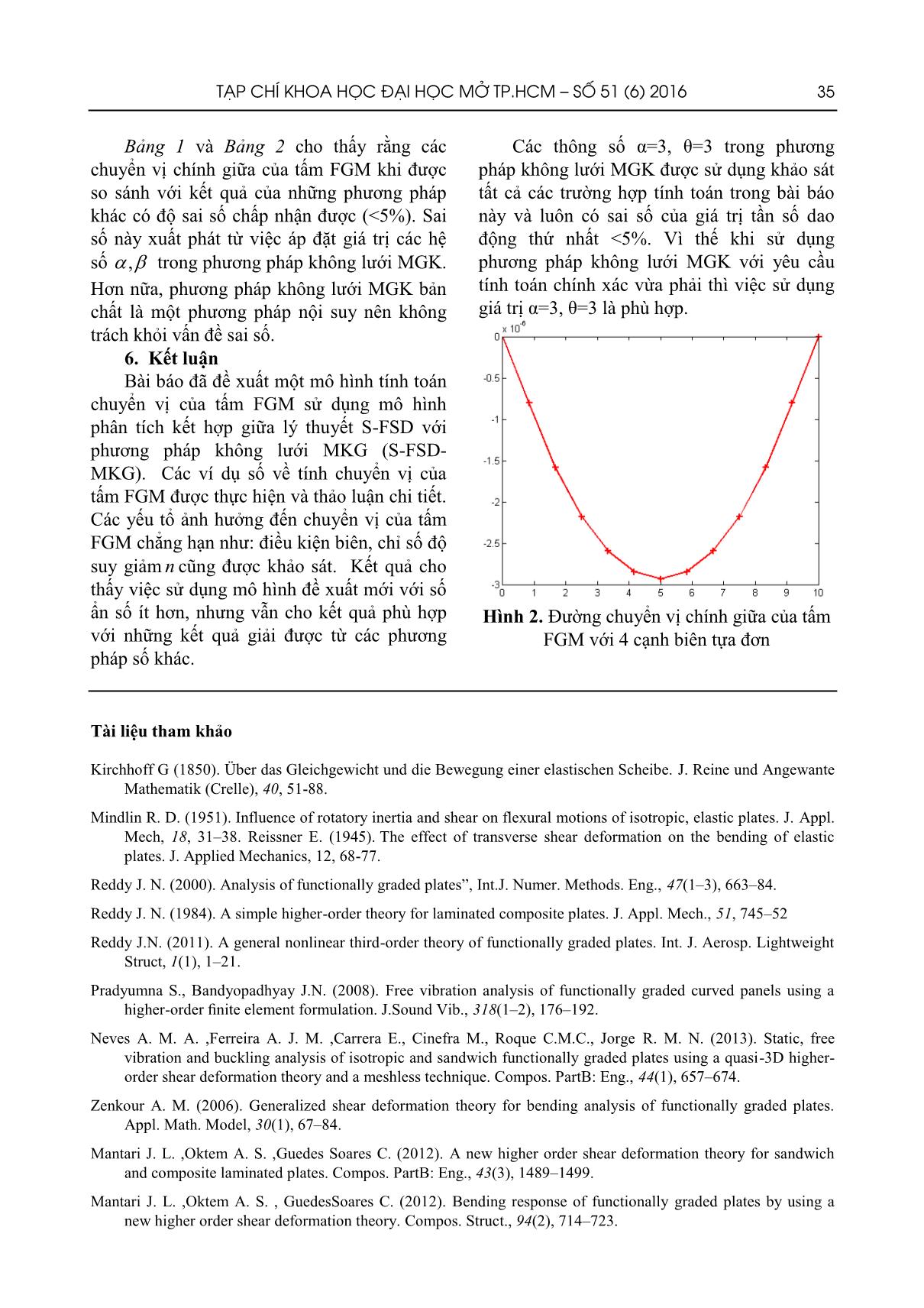
Trang 9

Trang 10
Tóm tắt nội dung tài liệu: Phân tích tĩnh của tấm FGM sử dụng phương pháp Mesh-Free và lý thuyết đơn giản biến dạng cắt bậc nhất

TẠP CHÍ KHOA HỌC ĐẠI HỌC MỞ TP.HCM – SỐ 51 (6) 2016 27 PHÂN TÍCH TĨNH CỦA TẤM FGM SỬ DỤNG PHƯƠNG PHÁP MESH-FREE VÀ LÝ THUYẾT ĐƠN GIẢN BIẾN DẠNG CẮT BẬC NHẤT NGUYỄN NGỌC HƯNG Trường Đại học Thủ Dầu Một - hungnn@tdmu.edu.vn, VŨ TÂN VĂN Trường Đại học Kiến Trúc Thành phố Hồ Chí Minh - van.vutan@uah.edu.vn NGUYỄN TRỌNG PHƯỚC Trường Đại học Mở Thành phố Hồ Chí Minh – phuoc.nt@ou.edu.vn NGUYỄN HUỲNH TẤN TÀI Trường Đại học Thủ Dầu Một - tainht@tdmu.edu.vn (Ngày nhận: 9/9/2016; Ngày nhận lại: 08/11/16; Ngày duyệt đăng: 14/11/2016) TÓM TẮT Bài báo này giới thiệu một mô hình số mới phân tích chuyển vị uốn của tấm vật liệu chức năng với các đặc tính vật liệu thay đổi theo chiều dày tấm. Mô hình này dựa trên phương pháp không lưới sử dụng hàm nội suy Moving Kriging (MK) kết hợp với lý thuyết biến dạng cắt bậc nhất đơn giản (S-FSD). Các ví dụ số được thực hiện để so sánh kết quả đạt được với các kết quả của các nghiên cứu đã công bố nhằm kiểm chứng sự chính xác của mô hình phân tích được đề xuất. Từ khóa: Chuyển vị; tấm vật liệu chức năng; lý thuyết biến dạng cắt bậc nhất đơn giản; nội suy Moving Kriging; phương pháp không lưới. Static bending analylis of FGM plates based on the meshless method and simple first- order shear deformation theory ABSTRACT This paper presents a new numerical model for analysing static bending of Functionally Graded Material (FGM) plates which material properties vary through the thickness. This model employed the mesh-free method with Moving Kriging (MK) interpolation with the simple first-order shear deformation(S-FSD) theory. Numerical examples are solved and the results are compared with reference solutions to confirm the accuracy of the proposed method. Keywords: Deflections; Functionally graded plates; Simple first-order shear deformation theory; Moving Kriging interpolation; mesh-free method. 1. Giới thiệu Vật liệu biến đổi chức năng (Functionally Graded Material- FGM) là một loại composite có đặc tính vật liệu biến đổi liên tục trong vật thể do đó sẽ loại bỏ được hiện tượng tập trung ứng suất thường gặp ở loại composite thông thường. FGM thường được chế tạo từ hỗn hợp gồm gốm và kim loại. Đây là loại vật liệu đẳng hướng nhưng không đồng nhất. Hiện nay, FGM được quan tâm vì có thể tạo ra những kết cấu có khả năng thích ứng với những điều kiện vận hành. Thông thường, phân tích ứng xử của tấm vật liệu chức năng dựa trên các lý thuyết cơ bản sau: (i) Tấm cổ điển (CP), (ii) Biến dạng cắt bậc nhất (FSD), (iii) Biến dạng cắt bậc cao (HSD). Lý thuyết CP (Kirchhoff G, 1850) không xét đến ảnh hưởng của biến dạng cắt ngang đến 28 KỸ THUẬT – CÔNG NGHỆ ứng xử của tấm mỏng. Khi chiều dày tấm tăng lên, biến dạng cắt ngang có ảnh hưởng đáng kể đến đáp ứng của tấm. Lý thuyết FSD đề xuất bởi Mindlin R. D. (1951) và Reissner E. (1945) xét đến ảnh hưởng biến dạng cắt này bằng cách xây dựng trường chuyển vị tuyến tính bậc nhất trong mặt phẳng dọc theo chiều dày của tấm. Tuy vậy, các phương trình cân bằng, ổn định được xây dựng dựa trên lý thuyết CPT và FSDT đều không thỏa mãn điều kiện biên về sự triệt tiêu ứng suất ở mặt trên và dưới của tấm. Nhằm giải quyết được khó khăn này, một hệ số điều chỉnh biến dạng cắt được sử dụng để điều chỉnh mối quan hệ kết hợp giữa ứng suất cắt và biến dạng cắt ngang. Giá trị hệ số điều chỉnh này phụ thuộc vào các thông số như: hình học, tải trọng tác dụng, điều kiện biên của tấm. Lý thuyết HSD đề xuất bởi Reddy J. N. (2000), Neves A. M. A. và cộng sự (2013) xét đến ảnh hưởng biến dạng cắt ngang bằng cách xây dựng các trường chuyển vị bậc cao ở trong mặt phẳng dọc theo chiều dày của tấm, hoặc theo mặt phẳng ngang của tấm. Các phương trình cân bằng, ổn định dựa trên trường chuyển vị đã thỏa mãn các tất cả điều kiện biên. Tuy vậy, việc phân tích ứng xử của tấm dựa trên các lý thuyết HSD này rất phức tạp do số lượng biến số ở các phương trình cân bằng, ổn định tăng lên, chẳng hạn hàm chuyển vị được xây dựng trên lý thuyết HSD đề xuất bởi Pradyumna và Bandyopadhyay (2008), Neves và cộng sự (2012-2013) sử dụng 9 ẩn số; Reddy (2011), Talha và Singh (2010) sử dụng lần lượt gồm 11, 13 ẩn số. Dù cho một số lý thuyết HSD khác sử dụng hàm chuyển vị gồm 5 ẩn số tương tự như lý thuyết FSD chẳng hạn như: lý thuyết biến dạng cắt bậc ba (TSD) (Reddy J. N. ,2000), lý thuyết biến dạng cắt hàm sin (Zenkour A. M., 2006), lý thuyết biến dạng cắt hàm lượng giác (Mantari J. L., Oktem A. S., Guedes Soares C., 2012) và (Mantari J. L., Oktem A. S., GuedesSoares C., 2012). Tuy vậy, phương trình cân bằng, ổn định đạt được từ các lý thuyết này vẫn phức tạp hơn so với lý thuyết biến dạng cắt bậc nhất (FSD). Lý thuyết biến dạng cắt bậc nhất đơn giản (S- FSD) được đề xuất đầu tiên bởi Huffington N.J. (1963) với hàm chuyển vị chỉ gồm 4 ẩn số. Khác với lý thuyết FSD, thành phần góc xoay được biểu diễn thông qua t ... ε 2 2 2 2 2 κ 2 b b b w x w y w x y γ s s w x w y (11.a,b,c) Mối quan hệ kết hợp thiết lập dựa trên luật Hooke bởi phương trình sau: 0σ = D (z)(ε - κ)m z τ = D ( )γs z (12a,b) với 0σ = D ( )(ε - κ)m z z τ T xz yz (13a,b) và 1 0 ( ) D (z) = 1 0 1- 0 0 (1- ) / 2 m 2 v E z v v v (14) 1 0 D = 0 12 1+ s kE z z v (15) Trong đó k là hệ số hiệu chỉnh cắt. 4. Mô hình phân tích 4.1. Hàm dạng MK Phương pháp MK được dùng để xây dựng hàm dạng và các đạo hàm theo Gu L. (2003) và Tongsuk P., Kanok-Nukulchai W. (2004). Giả thiết hàm phân bố xiu được xấp xỉ trong miền con x sao cho x . Giả sử rằng các giá trị của hàm số được nội suy dựa trên các giá trị tại các điểm nút x 1,i i n với n là tổng số điểm nút trong miền x . Hàm nội suy MK uh x , x x được xác định như sau: u (x) p (x)A r (x)B u(x)h T T (16) Hay 1 u (x) Φ ( )u n h I Ix (17 Trong đóΦ (x)I là hàm dạng MK, được xác định như sau Φ (x) p (x)A r (x)BT TI (18) A , B được định nghĩa như sau: 1 1 1A P R P P RT T (19) -1B = R (I - PA) (20) Trong đó I là ma trận đơn vị, véc tơ p(x) là đa thức với m hàm cơ sở : 1 2 3p ( ) (x), (x), (x)...., (x) T mx p p p p (21) Cụ thể, đối với ma trận P kích thước n m , các giá trị của hàm cơ sở đa thức (13) được cho bởi như sau: 1 1 2 1 1 1 2 2 2 2 1 2 (x ) (x ) (x ) (x ) (x ) (x ) P (x ) (x ) (x ) m m m m m m p p p p p p p p p (22) Véc tơ r(x) trong phương trình (16) được định nghĩa như sau: 1 2r ( ) (x ,x), x ,x ,.... x ,x T nx R R R (23) x ,xi jR là hàm tương quan giữa các cặp của n nút x i và x j nó được biểu hiện bằng các phương sai của các trường giá trị u(x) : TẠP CHÍ KHOA HỌC ĐẠI HỌC MỞ TP.HCM – SỐ 51 (6) 2016 31 R(x ,x ) cov (x ), (x )i j i ju u và R(x ,x) cov (x ), (x)i iu u . Có nhiều cách để xác định hàm (x , x )i jR nhưng phương pháp hàm Gauss là phương pháp thường sử dụng vì tính đơn giản, hiệu quả 2 ijR(x ,x ) r i j e (24) Với: ij x xi jr , và 0 là hệ số tương quan. Trong bài báo này sử dụng p (x)T là một hàm bậc hai như sau: 2 2p ( ) 1, , , , ,T x x y x y xy (25) Ngoài ra, ma trận . R ( , )i j n n R x x được biểu diễn dưới dạng tường minh như sau: 1 2 1 2 1 2 1 2 1 (x ,x ) (x ,x ) (x ,x ) 1 (x ,x ) R ( , ) (x ,x ) (x ,x ) 1 n n i j n n R R R R R x x R R (26) Đối với bài toán tấm FGM, không chỉ đạo hàm bậc 1 được sử dụng mà còn đạo hàm bậc 2 của hàm dạng cũng được thiết lập như sau: . , ,(x) (x) (x) m n I i j i jI k i kI j k p A r B (27) , , ,(x) (x) (x) m n I ii j ii jI k ii kI j k p A r B (28) Cần lưu ý ảnh hưởng của hệ số tương quan đối với hàm dạng là rõ ràng. Một trong những điểm quan trọng nhất của hàm dạng MK, đó là sở hữu tính chất Kronecker’s delta. Điều này sẽ loại bỏ những trở ngại đáng kể nhất của hầu hết các phương pháp không lưới khi áp đặt điều kiện biên để giải bài toán cơ học. Để chứng minh cho điều này, chúng ta khảo sát lại hàm dạng MK xác định bởi biểu thức (18). (x ) (x ) (x ) m n I j j j jI k j kI j k p A r B (29) Hay biểu thức (29) có thể viết dưới dạng sau: Φ (x ) PA RBI j (30) Trong đó ma trận và được định nghĩa bởi công thức (19) (20) và (22). Thay công thức (20) vào (30) ta được: 1Φ (x ) PA RR (I PA) II j (31) Biểu thức (31) dẫn đến tính chất Kronecker’s delta xác định bởi biểu thức (32). ij 1 khi Φ (x ) 0 khi I j i j i j (32) Ngoài ra, hàm nội suy MK sở hữu tính nhất quán, nghĩa là có thể xây dựng lại bất cứ hàm có bậc thấp hơn. Để đơn giản, thuộc tính này có thể tóm tắt như sau: Nếu u I đạt được từ đa thức có bậc nhỏ hơn hoặc bằng m nghĩa là u P (33) trong đó, P được xác định từ công thức (22) và là hệ số bất kỳ, thì sự xấp xỉ đó là chính xác. Sự xấp xỉ của trường chuyển vị như sau: (x) p (x) (x)h Tu u (34) Đặc biệt, nếu sử dụng hàm (x)p là hàm tuyến tính khi xây dựng hàm dạng MK thì tất cả hằng số, số hạng tuyến tính có thể xác định lại hoàn toàn: 1(x) 1, x , x n n n I I I I j j j x x y y (35) Mặt khác, một trong các yếu tố quan trọng đối với phương pháp không lưới là miền ảnh hưởng, trong đó bán kính miền ảnh hưởng được dùng để xác định số lượng các nút rời rạc trong phạm vi miền nội suy đang xét. Bán kính miền ảnh hưởng md được xác định như sau: s cd d (36) Trong đó là hệ số của miền giá đỡ, thông thường nằm trong khoảng từ 2.0 đến 3.0. Giá trị cd là chiều dài đặc trưng cho khoảng cách các nút với điểm đang xét. 4.2. Các phương trình rời rạc 32 KỸ THUẬT – CÔNG NGHỆ Những chuyển vị trong hệ tọa độ tổng quát trong mặt phẳng giữa được xấp xỉ theo biểu thức (17) trong đó : u T h h h h h b su v w w (37) Và u T I I I bI sIu v w w (38) Thay biểu thức (17) vào biểu thức (11,a,b,c) nhận được 0ε B u n m I I I κ = B u n b I I I B u n s I I I γ (39) Trong đó: , , , , 0 0 0 B 0 0 0 0 0 I x m I I y I y I x , , , 0 0 0 B 0 0 0 0 0 0 I xx b I I yy I xy , , 0 0 0 B 0 0 0 I xm I I y (40a,b,c) Với bài toán chuyển vị, dạng yếu được biểu diễn như sau: D D u mT T s Td d ud ε ε γ γ (41) Trong đó 0ε ε κ D B D B D m b /2 /2 D D ( ) h s s h z dz (42a,b,c) /2 /2 D D ( ) h m m h z dz /2 /2 B D ( ) h m h z z dz (43a,b) /2 2 /2 D D ( ) h b m h z z dz (44) với 0 1 1 2 m I I I I /2 2 0 1 2 /2 , , 1, , h h I I I z z z dz (45a,b) và 1 2 u u = u (46) 1 1 1 u N u h n h I I h h b s u v w + w (47) 2 2 / u / N u 0 h b n h b I I I w x w y (48) 1 0 0 0 N 0 0 0 0 0 I I I I I , 2 , 0 0 0 N 0 0 0 0 0 0 0 I x I I y (49a,b) Thay thế biểu thức (39) và (42a,b,c) vào biểu thức (41) bài toán chuyển vị của tấm FGM có thể viết lại như sau: 2K M d 0 (50) Trong đó ma trận độ cứng, khối lượng trong hệ tọa độ tổng thể xác định như sau: B D B B K B D B B B D B T m m m T s s s b b b d d (51) B D B B K B D B B B D B T m m m T s s s b b b d d (52) TẠP CHÍ KHOA HỌC ĐẠI HỌC MỞ TP.HCM – SỐ 51 (6) 2016 33 5. Kết quả số Trong phần này, chuyển vị của tấm FGM với chỉ số n suy giảm thay đổi cùng với các điều kiện biên khác nhau được khảo sát dựa trên mô hình phân tích kết hợp giữa lý thuyết S-FSD với phương pháp không lưới MKG (S- FSD-MKG). Lược đồ bậc 2 Gauss 4 4 được sử dụng trong phương pháp không lưới MKG để tích phân dạng yếu. Điều kiện biên của tấm được ký hiệu như sau: gối tựa đơn giản (S), ngàm (C), và tự do (F) . Các điều kiện biên này được áp đặt thông qua các phương trình được đề xuất bởi Shuohui Y và cộng sự (2014) như sau: (i) Cạnh biên gối tựa đơn: 0b sb s w w v w w y y , tại 0,x a . 0b sb s w w u w w x x , tại 0,y b . (ii) Cạnh biên gối tựa ngàm: 0b b s sb s w w w w u v w w x y x y , tại 0,x a và 0, .y b Bài toán 1: Tấm FGM hình vuông có chiều dày tấm 0,01h m được sản xuất từ vật liệu 2 3/Al Al O . Thuộc tính vật liệu của Al là: 0.3, 70m mv E GPa , và 32707 /m kg m , thuộc tính vật liệu của 2 3Al O là: 0.3cv , 380cE GPa và 33800 /c kg m . Tấm sử dụng số lượng điểm nút là13 13 . Hệ số hiệu chỉnh cắt 0.8601sk . Phương pháp không lưới MKG sử dụng các thông số: 3, 3 . Kết quả chuyển vị của tấm FGM có số liệu như trên với lực tác dụng vào tấm FGM là lực phân bố đều có giá trị là 1P . Chuyển vị được kiểm chứng trong bài toán là chuyển vị của điểm chính giữa tấm và không thứ nguyên được định nghĩa như sau: 3 2 4 100 12 1 m m m w E h w v PL . Bảng 1 Chuyển vị không thứ nguyên của tấm FGM so sánh với các phương pháp khác Type a h Method 0n 0.5n 1n 2n SSSS 5 S-FSDT - IGA (Shuohui) 0.1717 0.2324 0.2719 0.3115 FSDT - IGA (Shuohui) 0.1717 0.2324 0.2719 0.3115 FSDT - kpRitz (Shuohui) 0.1722 0.2403 0.2811 0.3221 FSDT- ES-DSG3 (Shuohui) 0.1703 0.2232 0.2522 0.2827 Bài báo 0.1777 0.2402 0.2803 0.3204 %(BB/Ritz) 3.18 -0.05 -0.29 -0.52 20 S-FSDT - IGA (Shuohui) 0.1440 0.1972 0.2310 0.2628 FSDT - IGA (Shuohui) 0.1440 0.1972 0.2310 0.2628 Bài báo 0.1507 0.2058 0.2403 0.2728 %(LV/ FSDT) 4.65 4.34 4.04 3.81 100 S-FSDT - IGA (Shuohui) 0.1423 0.1949 0.2284 0.2597 FSDT - IGA (Shuohui) 0.1423 0.1949 0.2284 0.2597 Bài báo 0.1490 0.2036 0.2378 0.2698 %(BB/ FSDT) 4.69 4.44 4.11 3.88 SFSF 5 S-FSDT - IGA (Shuohui) 0.5083 0.6918 0.8099 0.9247 FSDT - IGA (Shuohui) 0.5089 0.6926 0.8108 0.9258 34 KỸ THUẬT – CÔNG NGHỆ Bài báo 0.4939 0.6717 0.7858 0.8968 %(BB/ FSDT) -2.95 -3.01 -3.08 -3.13 20 S-FSDT - IGA (Shuohui) 0.4614 0.6319 0.7404 0.8420 FSDT - IGA (Shuohui) 0.4615 0.6321 0.7406 0.8422 Bài báo 0.4483 0.6135 0.7183 0.8164 %(BB/ FSDT) -2.86 -2.94 -3.02 -3.07 100 S-FSDT - IGA (Shuohui) 0.4584 0.6281 0.7360 0.8367 FSDT - IGA (Shuohui) 0.4584 0.6281 0.7360 0.8367 Bài báo 0.4454 0.6098 0.7139 0.8112 %(BB/ FSDT) -2.84 -2.91 -3.00 -3.05 Bài toán 2: Tiếp tục kiểm chứng kết quả chuyển vị của tấm FGM có số liệu như Bài toán 1, hệ nút 13 13 , 100a h , hệ số 3 , 3 , hệ số hiệu chỉnh cắt 0.8601.sk Lực tác dụng vào tấm là lực phân bố đều có giá trị là 1P . Chuyển vị được kiểm chứng trong bài toán là chuyển vị của điểm chính giữa tấm và chuyển vị này không thứ nguyên được định nghĩa như sau: 3 4 10 c mw E hw PL . Bảng 2 Chuyển vị chính giữa tấm FGM có 100a h với các điều kiện biên khác nhau Type Method n = 0 n = 0.5 n = 1 n = 2 n = 5 n = 10 SSSS S-FSDT 0.4438 0.6846 0.8904 1.1411 1.3494 1.4816 FSDT 0.4438 0.6847 0.8904 1.1411 1.3494 1.4816 Bài báo 0.4648 0.7132 0.9204 1.1696 1.3873 1.5357 %(BB/FSDT) 4.73 4.16 3.37 2.50 2.81 3.65 SFSF S-FSDT 1.4302 2.2062 2.8692 3.6770 4.3483 4.7740 FSDT 1.4302 2.2062 2.8693 3.6770 4.3483 4.7740 Bài báo 1.3896 2.1405 2.7781 3.5525 4.2042 4.6257 %(BB/FSDT) -2.84 -2.98 -3.18 -3.39 -3.31 -3.11 SCSC S-FSDT 0.2096 0.3232 0.4204 0.5387 0.6372 0.6996 FSDT 0.2097 0.3234 0.4205 0.5389 0.6375 0.7000 Bài báo 0.2066 0.3158 0.4053 0.5123 0.6088 0.6777 %(BB/FSDT) -1.48 -2.35 -3.60 -4.94 -4.50 -3.19 CCCC S-FSDT 0.1384 0.2135 0.2776 0.3557 0.4208 0.4621 FSDT 0.1384 0.2135 0.2776 0.3558 0.4209 0.4622 Bài báo 0.1370 0.2104 0.2719 0.3460 0.4103 0.4535 %(BB/FSDT) -1.02 -1.46 -2.07 -2.76 -2.53 -1.87 TẠP CHÍ KHOA HỌC ĐẠI HỌC MỞ TP.HCM – SỐ 51 (6) 2016 35 Bảng 1 và Bảng 2 cho thấy rằng các chuyển vị chính giữa của tấm FGM khi được so sánh với kết quả của những phương pháp khác có độ sai số chấp nhận được (<5%). Sai số này xuất phát từ việc áp đặt giá trị các hệ số , trong phương pháp không lưới MGK. Hơn nữa, phương pháp không lưới MGK bản chất là một phương pháp nội suy nên không trách khỏi vấn đề sai số. 6. Kết luận Bài báo đã đề xuất một mô hình tính toán chuyển vị của tấm FGM sử dụng mô hình phân tích kết hợp giữa lý thuyết S-FSD với phương pháp không lưới MKG (S-FSD- MKG). Các ví dụ số về tính chuyển vị của tấm FGM được thực hiện và thảo luận chi tiết. Các yếu tổ ảnh hưởng đến chuyển vị của tấm FGM chẳng hạn như: điều kiện biên, chỉ số độ suy giảm n cũng được khảo sát. Kết quả cho thấy việc sử dụng mô hình đề xuất mới với số ẩn số ít hơn, nhưng vẫn cho kết quả phù hợp với những kết quả giải được từ các phương pháp số khác. Các thông số α=3, θ=3 trong phương pháp không lưới MGK được sử dụng khảo sát tất cả các trường hợp tính toán trong bài báo này và luôn có sai số của giá trị tần số dao động thứ nhất <5%. Vì thế khi sử dụng phương pháp không lưới MGK với yêu cầu tính toán chính xác vừa phải thì việc sử dụng giá trị α=3, θ=3 là phù hợp. Hình 2. Đường chuyển vị chính giữa của tấm FGM với 4 cạnh biên tựa đơn Tài liệu tham khảo Kirchhoff G (1850). Über das Gleichgewicht und die Bewegung einer elastischen Scheibe. J. Reine und Angewante Mathematik (Crelle), 40, 51-88. Mindlin R. D. (1951). Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech, 18, 31–38. Reissner E. (1945). The effect of transverse shear deformation on the bending of elastic plates. J. Applied Mechanics, 12, 68-77. Reddy J. N. (2000). Analysis of functionally graded plates”, Int.J. Numer. Methods. Eng., 47(1–3), 663–84. Reddy J. N. (1984). A simple higher-order theory for laminated composite plates. J. Appl. Mech., 51, 745–52 Reddy J.N. (2011). A general nonlinear third-order theory of functionally graded plates. Int. J. Aerosp. Lightweight Struct, 1(1), 1–21. Pradyumna S., Bandyopadhyay J.N. (2008). Free vibration analysis of functionally graded curved panels using a higher-order finite element formulation. J.Sound Vib., 318(1–2), 176–192. Neves A. M. A. ,Ferreira A. J. M. ,Carrera E., Cinefra M., Roque C.M.C., Jorge R. M. N. (2013). Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher- order shear deformation theory and a meshless technique. Compos. PartB: Eng., 44(1), 657–674. Zenkour A. M. (2006). Generalized shear deformation theory for bending analysis of functionally graded plates. Appl. Math. Model, 30(1), 67–84. Mantari J. L. ,Oktem A. S. ,Guedes Soares C. (2012). A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. PartB: Eng., 43(3), 1489–1499. Mantari J. L. ,Oktem A. S. , GuedesSoares C. (2012). Bending response of functionally graded plates by using a new higher order shear deformation theory. Compos. Struct., 94(2), 714–723. 36 KỸ THUẬT – CÔNG NGHỆ Neves A. M. A., Ferreira A. J. M., Carrera E., Cinefra M., Roque C. M. C., Jorge R. M. N. (2012). A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos. Struct., 94(5), 1814–1825. Huffington N.J. (1963). Response of elastic columns to axial pulse loading. A.I.A.A. J., 1(9), 2099–2104. Chen X. L. ,Liew K. M. (2004). Buckling of rectangular functionally graded material plates subjected to nonlinearly distributed in-plane edge loads. Smart. Mater. Struct., 13(6), 1430-1441. Gu L. (2003). Moving Kriging interpolation and element free Galerkin method. Int. J. Num. Meth. Eng., 56, 1–11. Tongsuk P., Kanok-Nukulchai W. (2004). Further investigation of element free Galerkin method using moving Kriging interpolation. Int. J. Com. Meth., 1, 1–21. Shuohui Y., Jack S. H., Tiantang Y.,Tinh Q. B., Stéphane P.A.B. (2014). Isogeometric locking-free plate element: A simple first order shear deformation theory for functionally graded plates. Comp. Strut., 118, 121-138.
File đính kèm:
 phan_tich_tinh_cua_tam_fgm_su_dung_phuong_phap_mesh_free_va.pdf
phan_tich_tinh_cua_tam_fgm_su_dung_phuong_phap_mesh_free_va.pdf

