Phân tích sụp đổ lan truyền trong cầu dây văng bằng phương pháp phần tử hữu hạn
Trong cầu dây văng, hệ dây văng làm nhiệm vụ đỡ dầm giúp cầu có thể vượt được những khẩu độ lớn cho nên hiện tượng lan truyền đứt cáp từ một cáp bị sự cố đứt cáp là bài toán thu hút nhiều sự quan tâm của các nhà khoa học. Bên cạnh đó,khi cáp bị đứt dầm sẽ bị phá hoại hoặc do ứng suất vượt quá giới hạn cho phép hoặc do mất ổn định cục bộ. Bài báo này phân tích các kịch bản đứt cáp trong cầu và phân tích hiện tượng mất ổn định cục bộ của dầm tương ứng với các kịch bản đứt cáp nói trên. Hiện tượng đứt cáp được mô hình bằng lực thay đổi đột ngột theo thời gian. Kết quả của bài báo chỉ ra hiện hiện tượng lan truyền đứt cáp trong cầu và khi nào hiện tượng sụp đổ lan truyền sẽ xảy ra.

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
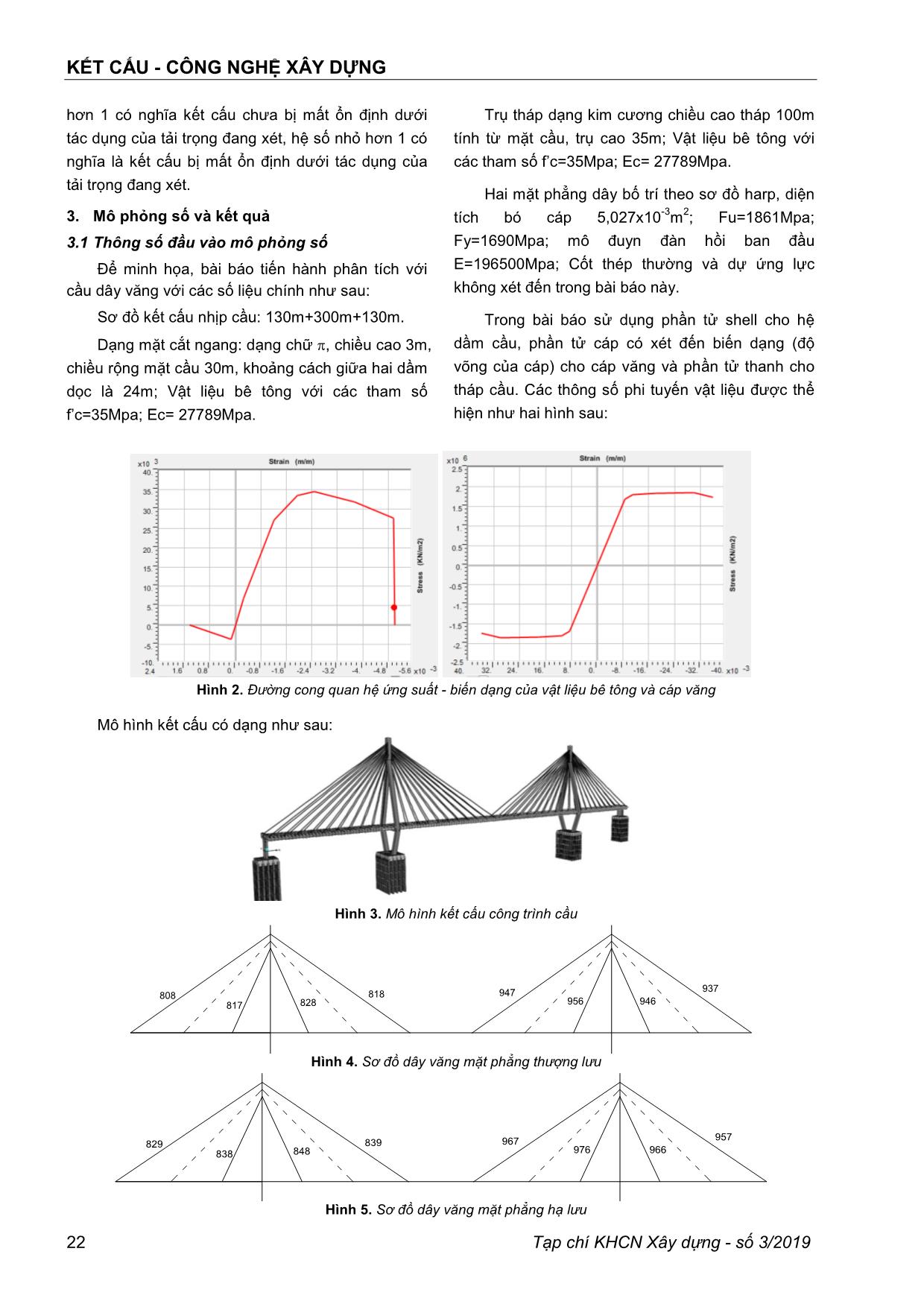
Trang 6

Trang 7
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Phân tích sụp đổ lan truyền trong cầu dây văng bằng phương pháp phần tử hữu hạn

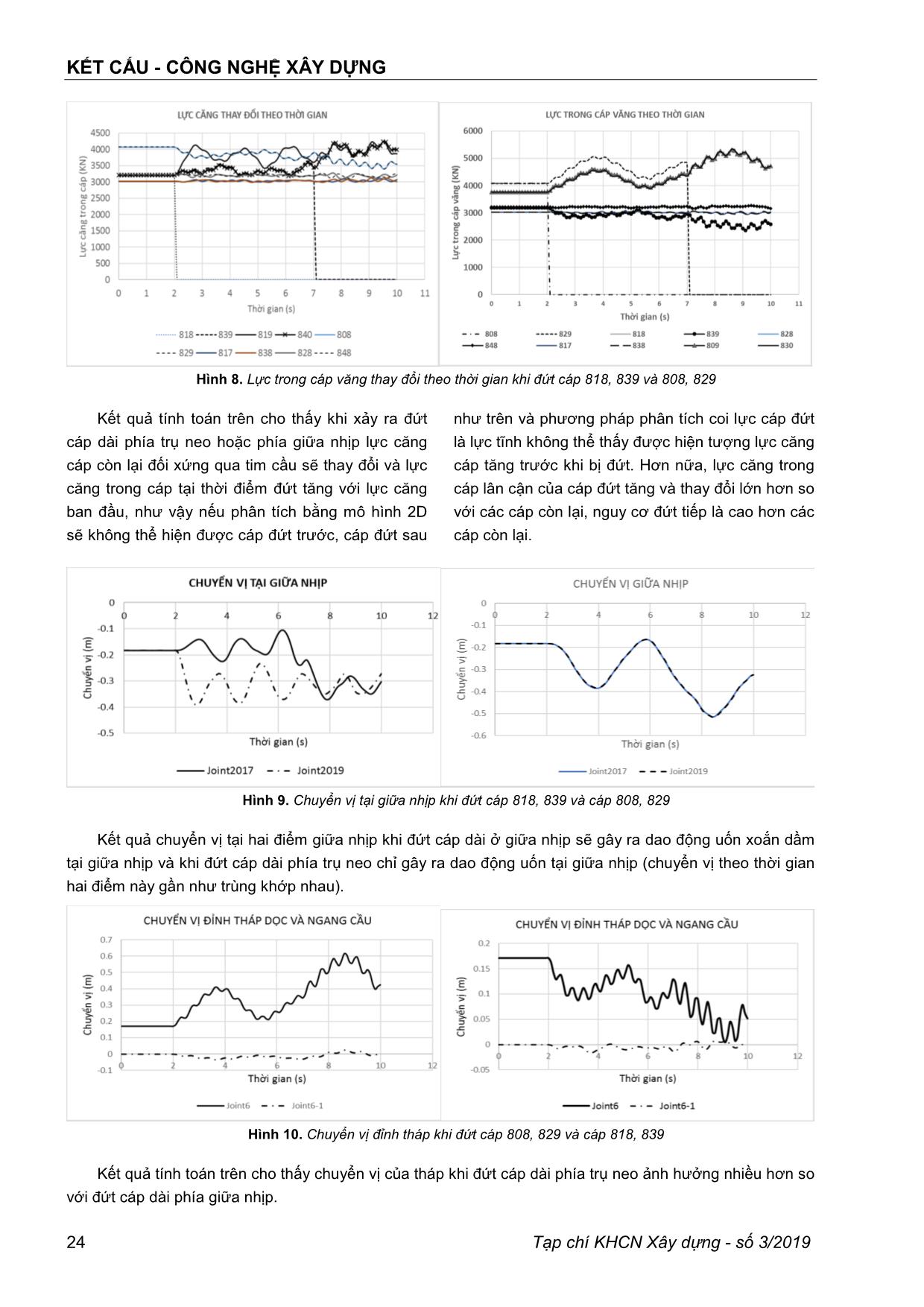
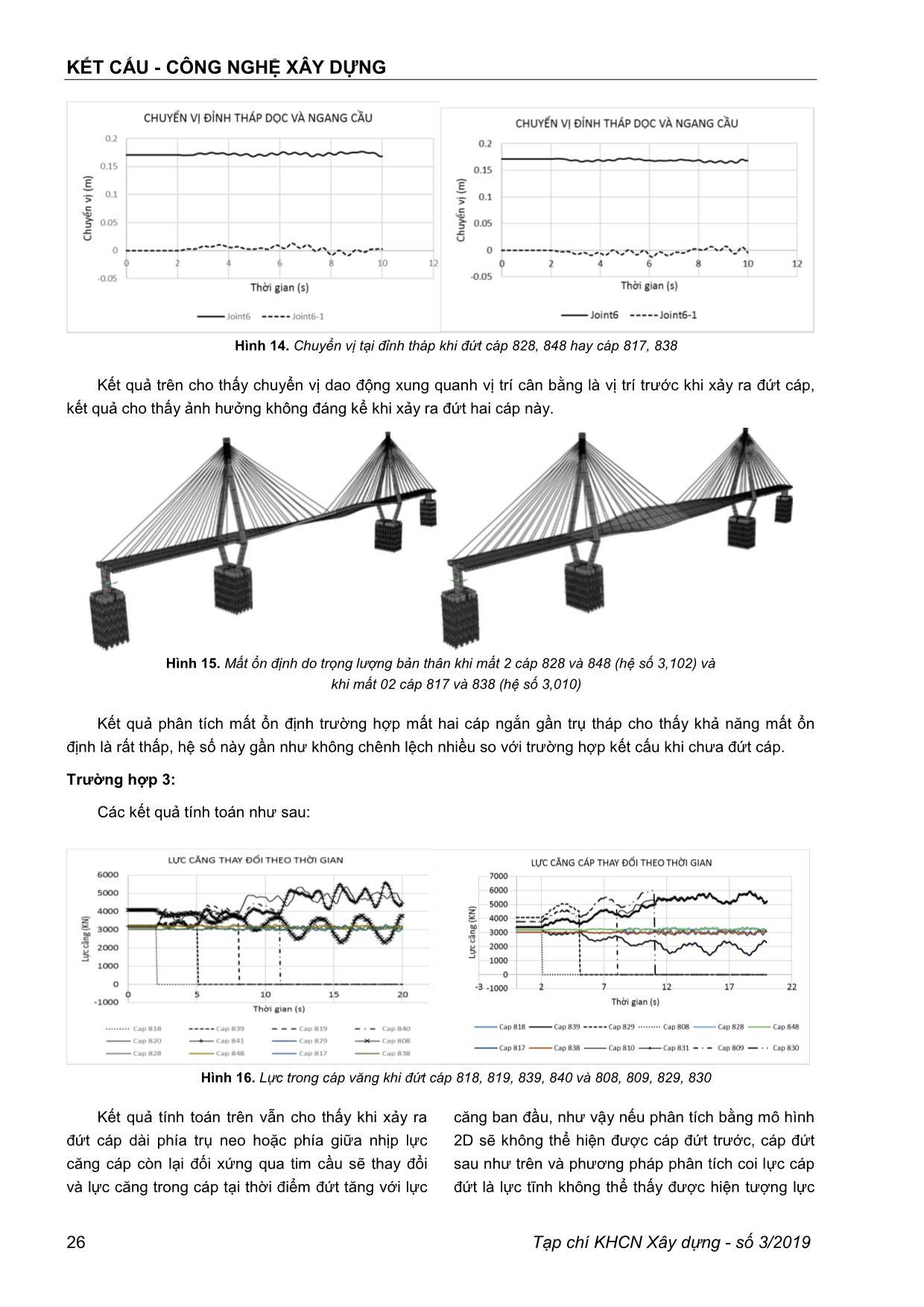
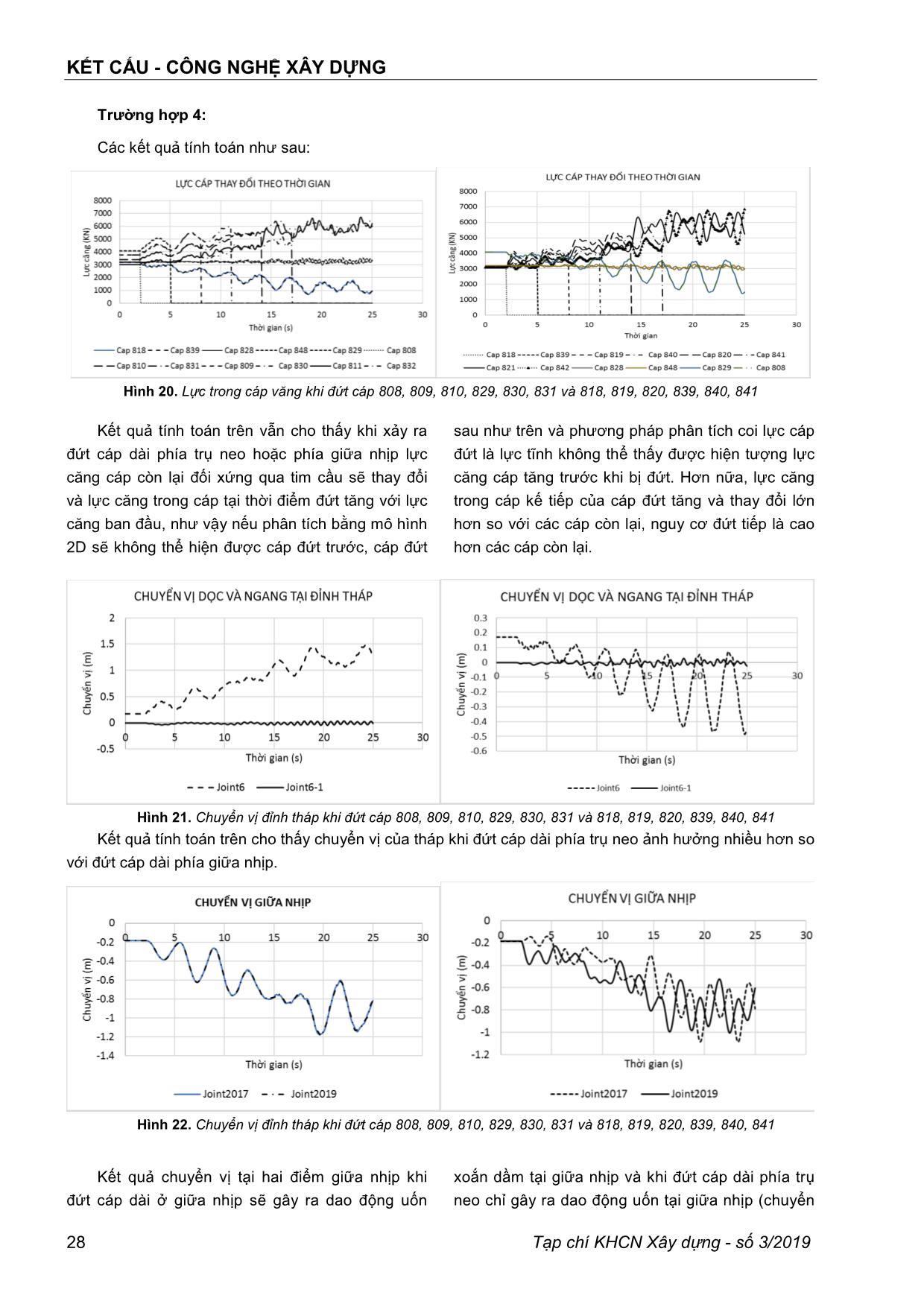
KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 19 PHÂN TÍCH SỤP ĐỔ LAN TRUYỀN TRONG CẦU DÂY VĂNG BẰNG PHƢƠNG PHÁP PHẦN TỬ HỮU HẠN PGS.TS. NGUYỄN HỮU HƢNG Trường đại học Giao thông vận tải Tóm tắt: Trong cầu dây văng, hệ dây văng làm nhiệm vụ đỡ dầm giúp cầu có thể vượt được những khẩu độ lớn cho nên hiện tượng lan truyền đứt cáp từ một cáp bị sự cố đứt cáp là bài toán thu hút nhiều sự quan tâm của các nhà khoa học. Bên cạnh đó, khi cáp bị đứt dầm sẽ bị phá hoại hoặc do ứng suất vượt quá giới hạn cho phép hoặc do mất ổn định cục bộ. Bài báo này phân tích các kịch bản đứt cáp trong cầu và phân tích hiện tượng mất ổn định cục bộ của dầm tương ứng với các kịch bản đứt cáp nói trên. Hiện tượng đứt cáp được mô hình bằng lực thay đổi đột ngột theo thời gian. Kết quả của bài báo chỉ ra hiện hiện tượng lan truyền đứt cáp trong cầu và khi nào hiện tượng sụp đổ lan truyền sẽ xảy ra. Từ khóa: sụp đổ lan truyền (Sập đổ dây chuyền, sập đổ lũy tiến), phân tích lịch sử thời gian phi tuyến, đứt cáp, phân tích mất ổn định Abstract: In the cable-stayed bridge, the cable- stayed system support girder helps the bridge to overcome large span so the phenomena of cable rupture progressive from a ruptured cable is the problem attracted the attention of scientists. Besides, when the cable is ruptured, the beam will be damaged either due to the stress exceeding the allowed limit or due to local instability. This paper analyzes the cable rupture scenarios in the bridge and analyzes buckling of beams corresponding to the above cable rupture scenarios. The phenomenon of cable rupture is modeled by force changed over time. The results of the paper show that the phenomenon of cable rupture in the bridge and when the phenomenon of progressive collapse will happen. Keywords: Progressive collapse, Nonlinear time history analysis, Cable rupture, Buckling analysis 1. Giới thiệu Cầu dây văng đã và đang được xây dựng phổ biến tại Việt Nam, từ cầu dây văng đầu tiên được hoàn thành năm 2000 (cầu Mỹ Thuận) đến nay Việt Nam đã có khoảng 20 cầu dây văng nhịp lớn hơn 150m. Trong kết cấu cầu dây văng hệ cáp văng là kết cấu được quan tâm nhiều vì chính hệ này đem lại sự ưu việt vượt trội của cầu dây văng so với các loại kết cấu khác. Trong thiết kế cầu dây văng một sự cố đã được đưa vào tính toán trong giai đoạn thiết kế đó là sự cố đứt cáp. Theo hướng dẫn của PTI (Post-Tensioning Institute) [1] coi lực đứt cáp như là lực tĩnh độ lớn bằng lực căng cáp và nhân thêm hệ số bằng 2 (hệ số xung kích) hoặc là phân tích lịch sử thời gian phi tuyến với hiện tượng này. Cách tính coi đứt cáp như lực tĩnh thuận lợi cho kỹ sư thiết kế nhưng chưa phản ánh hết được tương tác giữa cáp đứt với các cáp còn lại cũng như đối với các bộ phận của kết cấu khác. Trong hướng dẫn của PTI cho phép khi bị đứt một cáp bất kỳ thì cầu vẫn phải giữ được ổn định không xảy ra sụp đổ lan truyền trong kết cấu. Như vậy, khi nào cầu dây văng xảy ra hiện tượng sụp đổ lan truyền trở thành vấn đề được nhiều nhà nghiên cứu quan tâm, như các nghiên cứu của M. Wolff và U. Starossek [2,3]. Trong nghiên cứu của mình tác giả đã sử dụng mô hình phi tuyến để phân tích ứng xử của các bộ phận cầu dây văng dưới tác dụng của tải trọng đứt cáp, tác giả tập trung phân tích phản ứng của dầm và tháp với các trường hợp hệ số cản khác nhau để tìm ra hệ số động phù hợp cho các bộ phận này. Thông qua phân tích phi tuyến nhóm tác giả này cũng chỉ ra với trường hợp đứt một cáp thì cầu vẫn ổn định, chỉ khi đứt 3 cáp liền kề nhau cầu mới xảy ra sụp đổ. Qua phân tích cũng chỉ ra cách tăng cường chống lại sụp đổ lan truyền cho cầu dây văng bằng cách bố trí khoảng cách giữa các dây văng gần nhau hơn. Bên cạnh những nghiên cứu chuyên sâu của M. Wolff và U. Starossek về sụp đổ lan truyền trong cầu dây văng, hiện tượng lan truyền đứt cáp từ một cáp bị sự cố ban đầu là bài toán phức tạp thu hút nhiều sự quan tâm [4-8]. Trên thế giới nghiên cứu về bài toán đứt cáp đã được thực hiện từ những năm 1994 bởi E. Hyttinen và các cộng sự [4]. Bên cạnh những nghiên cứu của KẾT CẤU - CÔNG NGHỆ XÂY DỰNG 20 Tạp chí KHCN Xây dựng - số 3/2019 các nhà khoa học, bài toán này được quan tâm đặc biệt sau sự kiện 11/9/2001 ở Mỹ và đã có các hướng dẫn như những qui định về chống sụp đổ lan truyền đối với tòa nhà [9], và các hướng dẫn thiết kế sụp đổ lan truyền [10]. Nghiên cứu về bài toán đứt cáp cầu dây văng hay sụp đổ lan truyền trong cầu dây văng tại Việt Nam chưa có nhiều, một số bài báo có đóng góp của tác giả Việt Nam có thể kể đến như bài báo của tác giả Hoàng Vũ và các cộng sự [5], trong bài báo này nhóm tác giả vừa nghiên cứu lý thuyết vừa nghiên cứu thực nghiệm hiện tượng đứt cáp. Các nghiên cứu thực nghiệm làm rõ hơn cơ chế phá hoại cũng như độ lớn của hệ số động lấy vào khi phân tích tĩnh, cách làm hay được các kỹ sư s ... o 3m, chiều rộng mặt cầu 30m, khoảng cách giữa hai dầm dọc là 24m; Vật liệu bê tông với các tham số f’c=35Mpa; Ec= 27789Mpa. Trụ tháp dạng kim cương chiều cao tháp 100m tính từ mặt cầu, trụ cao 35m; Vật liệu bê tông với các tham số f’c=35Mpa; Ec= 27789Mpa. Hai mặt phẳng dây bố trí theo sơ đồ harp, diện tích bó cáp 5,027x10 -3 m 2 ; Fu=1861Mpa; Fy=1690Mpa; mô đuyn đàn hồi ban đầu E=196500Mpa; Cốt thép thường và dự ứng lực không xét đến trong bài báo này. Trong bài báo sử dụng phần tử shell cho hệ dầm cầu, phần tử cáp có xét đến biến dạng (độ võng của cáp) cho cáp văng và phần tử thanh cho tháp cầu. Các thông số phi tuyến vật liệu được thể hiện như hai hình sau: Hình 2. Đường cong quan hệ ứng suất - biến dạng của vật liệu bê tông và cáp văng Mô hình kết cấu có dạng như sau: Hình 3. Mô hình kết cấu công trình cầu 828 946 808 947 817 956 818 937 Hình 4. Sơ đồ dây văng mặt phẳng thượng lưu 839 957 829 967 838 976848 966 Hình 5. Sơ đồ dây văng mặt phẳng hạ lưu KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 23 Tải trọng tác dụng ban đầu là trọng lượng bản thân của kết cấu. Tải trọng đứt cáp được miêu tả là tải trọng thay đổi theo thời gian độ lớn bằng lực căng, hiện tượng đứt xảy ra trong 0,01s như minh họa ở hình bên dưới. 839(818) 957(937) t1 829(808) 967(947) P(KN) t2 t2-t1=0.01s 838(817) 976(956) t(s)T0 848(828) 966(946) T0 T0 Hình 6. Minh họa tải trọng đứt cáp Bài toán phân tích: đứt cáp với các kịch bản khác nhau đồng thời chịu tác dụng của trọng lượng bản thân. Quá trình tính toán được hỗ trợ bằng phần mềm CSI bridge v20 [11], với các thông số phi tuyến như sau: Hình 7. Các tham số khi phân tích phi tuyến 3.2 Các trường hợp tính toán và kết quả a. Các trường hợp tiến hành phân tích như sau: Do sau thời gian khai thác cáp văng bị hư hỏng, ăn mòn và bị mỏi nên hiện tượng đứt cáp là một sự cố (tai nạn) đối với công trình vậy bài báo giả thiết đứt cáp theo các kịch bản như sau: - Trường hợp 1: đứt dây dài phía trụ neo (cáp 808, 829) hoặc phía giữa nhịp (cáp 818, 839); - Trường hợp 2: đứt dây ngắn phía trụ neo (cáp 817, 838) hoặc phía giữa nhịp (cáp 828, 848); - Trường hợp 3: đứt dây dài và dây kế tiếp phía trụ neo (cáp 808, 809 và 829, 830) hoặc phía giữa nhịp (cáp 818, 819 và 839, 840); - Trường hợp 4: đứt dây dài và 02 dây kế tiếp phía trụ neo (cáp 808, 809, 810 và 829, 830, 831) hoặc phía giữa nhịp (cáp 818, 819, 820 và 839, 840, 841). Các trường hợp trên miêu tả theo trật tự thời gian như sau: dây đầu tiên (thượng lưu) đứt ở thời điểm 2s, dây tiếp theo (hạ lưu) đứt ở 5s (7s), tiếp tục các dây tiếp theo đứt ở thời điểm 8s, 11s, 14s và 17s. Để thấy được phản ứng uốn xoắn đồng thời của dầm chuyển vị tại hai điểm phía thượng lưu và hạ lưu được thể hiện để phân tích (tương ứng là nút 2019 và 2017). Để làm rõ phản ứng của tháp, chuyển vị đỉnh tháp theo phương dọc cầu và ngang cầu được thể hiện (tương ứng là nút số 6). Để thấy rõ sự lan truyền hiện tượng đứt cáp bài báo thể hiện sự thay đổi theo thời gian lực căng trong dây ứng với các trường hợp đứt cáp miêu tả ở trên. Cuối cùng để có thể kiểm tra xem kết cấu có sụp đổ hay không bài toán phân tích ổn định cục bộ được tiến hành sau mỗi kịch bản đứt cáp như đã miêu tả ở trên. b. Kết quả tính toán Trƣờng hợp 1: Các kết quả tính toán như sau: KẾT CẤU - CÔNG NGHỆ XÂY DỰNG 24 Tạp chí KHCN Xây dựng - số 3/2019 Hình 8. Lực trong cáp văng thay đổi theo thời gian khi đứt cáp 818, 839 và 808, 829 Kết quả tính toán trên cho thấy khi xảy ra đứt cáp dài phía trụ neo hoặc phía giữa nhịp lực căng cáp còn lại đối xứng qua tim cầu sẽ thay đổi và lực căng trong cáp tại thời điểm đứt tăng với lực căng ban đầu, như vậy nếu phân tích bằng mô hình 2D sẽ không thể hiện được cáp đứt trước, cáp đứt sau như trên và phương pháp phân tích coi lực cáp đứt là lực tĩnh không thể thấy được hiện tượng lực căng cáp tăng trước khi bị đứt. Hơn nữa, lực căng trong cáp lân cận của cáp đứt tăng và thay đổi lớn hơn so với các cáp còn lại, nguy cơ đứt tiếp là cao hơn các cáp còn lại. Hình 9. Chuyển vị tại giữa nhịp khi đứt cáp 818, 839 và cáp 808, 829 Kết quả chuyển vị tại hai điểm giữa nhịp khi đứt cáp dài ở giữa nhịp sẽ gây ra dao động uốn xoắn dầm tại giữa nhịp và khi đứt cáp dài phía trụ neo chỉ gây ra dao động uốn tại giữa nhịp (chuyển vị theo thời gian hai điểm này gần như trùng khớp nhau). Hình 10. Chuyển vị đỉnh tháp khi đứt cáp 808, 829 và cáp 818, 839 Kết quả tính toán trên cho thấy chuyển vị của tháp khi đứt cáp dài phía trụ neo ảnh hưởng nhiều hơn so với đứt cáp dài phía giữa nhịp. KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 25 Hình 11. Dạng mất ổn định do trọng lượng bản thân khi chưa mất cáp (hệ số 3,064); khi mất 2 cáp 818 và 839 (hệ số 2,003); khi mất 2 cáp 808 và 829 (hệ số 2,057). Kết quả trên cho thấy khi bị mất hai cáp dài cầu vẫn chưa bị mất ổn định nhưng hệ số ổn định đã giảm nhiều so với trước khi đứt cáp. Trƣờng hợp 2: Các kết quả tính toán như sau: Hình 12. Lực trong cáp văng thay đổi theo thời gian khi đứt cáp 848, 828 hay 817, 838 Kết quả trên cho thấy ảnh hưởng của sự cố đứt các cáp ngắn gần trụ tháp không gây ra ảnh hưởng nhiều so với các cáp còn lại mà chỉ ảnh hưởng nhỏ đến các cáp liền kề. Hình 13. Chuyển vị tại giữa nhịp khi đứt cáp 828, 848 hay cáp 817, 838 Kết quả trên cho thấy chuyển vị dao động xung quanh vị trí cân bằng là vị trí trước khi xảy ra đứt cáp, kết quả cho thấy ảnh hưởng không đáng kể khi xảy ra đứt hai tổ hợp cáp này. KẾT CẤU - CÔNG NGHỆ XÂY DỰNG 26 Tạp chí KHCN Xây dựng - số 3/2019 Hình 14. Chuyển vị tại đỉnh tháp khi đứt cáp 828, 848 hay cáp 817, 838 Kết quả trên cho thấy chuyển vị dao động xung quanh vị trí cân bằng là vị trí trước khi xảy ra đứt cáp, kết quả cho thấy ảnh hưởng không đáng kể khi xảy ra đứt hai cáp này. Hình 15. Mất ổn định do trọng lượng bản thân khi mất 2 cáp 828 và 848 (hệ số 3,102) và khi mất 02 cáp 817 và 838 (hệ số 3,010) Kết quả phân tích mất ổn định trường hợp mất hai cáp ngắn gần trụ tháp cho thấy khả năng mất ổn định là rất thấp, hệ số này gần như không chênh lệch nhiều so với trường hợp kết cấu khi chưa đứt cáp. Trƣờng hợp 3: Các kết quả tính toán như sau: Hình 16. Lực trong cáp văng khi đứt cáp 818, 819, 839, 840 và 808, 809, 829, 830 Kết quả tính toán trên vẫn cho thấy khi xảy ra đứt cáp dài phía trụ neo hoặc phía giữa nhịp lực căng cáp còn lại đối xứng qua tim cầu sẽ thay đổi và lực căng trong cáp tại thời điểm đứt tăng với lực căng ban đầu, như vậy nếu phân tích bằng mô hình 2D sẽ không thể hiện được cáp đứt trước, cáp đứt sau như trên và phương pháp phân tích coi lực cáp đứt là lực tĩnh không thể thấy được hiện tượng lực KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 27 căng cáp tăng trước khi bị đứt. Hơn nữa, lực căng trong cáp kế tiếp của cáp đứt tăng và thay đổi lớn hơn so với các cáp còn lại, nguy cơ đứt tiếp là cao hơn các cáp còn lại. Hình 17. Chuyển vị giữa nhịp khi đứt cáp 808, 809, 829, 830 và cáp 818, 819, 839, 840 Kết quả chuyển vị tại hai điểm giữa nhịp khi đứt cáp dài ở giữa nhịp sẽ gây ra dao động uốn xoắn dầm tại giữa nhịp và khi đứt cáp dài phía trụ neo chỉ gây ra dao động uốn tại giữa nhịp (chuyển vị theo thời gian hai điểm này gần như trùng khớp nhau). Hình 18. Chuyển vị đỉnh tháp khi đứt cáp 808, 809, 829, 830 và 818, 819, 839, 840 Kết quả tính toán trên cho thấy chuyển vị của tháp khi đứt cáp dài phía trụ neo ảnh hưởng nhiều hơn so với đứt cáp dài phía giữa nhịp. Hình 19. Mất ổn định do trọng lượng bản thân khi mất 04 cáp 808, 809 và 829, 830 (hệ số 1.8158) khi mất 04 cáp 818, 819 và 839, 840 (hệ số 1.2109) Kết quả tính toán ở trên cho thấy đã có sự giảm rõ rệt về hệ số ổn định khi đứt 02 cáp dài, hay nói cách khác khi đứt hai cáp nguy cơ xảy ra mất ổn định là rất lớn. KẾT CẤU - CÔNG NGHỆ XÂY DỰNG 28 Tạp chí KHCN Xây dựng - số 3/2019 Trƣờng hợp 4: Các kết quả tính toán như sau: Hình 20. Lực trong cáp văng khi đứt cáp 808, 809, 810, 829, 830, 831 và 818, 819, 820, 839, 840, 841 Kết quả tính toán trên vẫn cho thấy khi xảy ra đứt cáp dài phía trụ neo hoặc phía giữa nhịp lực căng cáp còn lại đối xứng qua tim cầu sẽ thay đổi và lực căng trong cáp tại thời điểm đứt tăng với lực căng ban đầu, như vậy nếu phân tích bằng mô hình 2D sẽ không thể hiện được cáp đứt trước, cáp đứt sau như trên và phương pháp phân tích coi lực cáp đứt là lực tĩnh không thể thấy được hiện tượng lực căng cáp tăng trước khi bị đứt. Hơn nữa, lực căng trong cáp kế tiếp của cáp đứt tăng và thay đổi lớn hơn so với các cáp còn lại, nguy cơ đứt tiếp là cao hơn các cáp còn lại. Hình 21. Chuyển vị đỉnh tháp khi đứt cáp 808, 809, 810, 829, 830, 831 và 818, 819, 820, 839, 840, 841 Kết quả tính toán trên cho thấy chuyển vị của tháp khi đứt cáp dài phía trụ neo ảnh hưởng nhiều hơn so với đứt cáp dài phía giữa nhịp. Hình 22. Chuyển vị đỉnh tháp khi đứt cáp 808, 809, 810, 829, 830, 831 và 818, 819, 820, 839, 840, 841 Kết quả chuyển vị tại hai điểm giữa nhịp khi đứt cáp dài ở giữa nhịp sẽ gây ra dao động uốn xoắn dầm tại giữa nhịp và khi đứt cáp dài phía trụ neo chỉ gây ra dao động uốn tại giữa nhịp (chuyển KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 29 vị theo thời gian hai điểm này gần như trùng khớp nhau). Hình 23. Mất ổn định do trọng lượng bản thân khi mất 6 cáp 818, 819, 820 và 839, 840, 841 (hệ số 0.4222) khi mất 6 cáp 808, 809, 810 và 829, 830, 831 (hệ số 0.8294) Kết quả thể hiện ở trên cho thấy khi mất 3 cáp dài hai phía liên tiếp thì cầu dây văng với các số liệu như trên sẽ xảy ra hiện tượng sụp đổ do mất ổn định. Như vậy đối với cầu trên sẽ có một kịch bản sụp đổ lan truyền xảy ra đó là đứt lần lượt 6 cáp và cầu bị mất ổn định dẫn đến bị phá hoại. 4. Phân tích kết quả Từ hình 8 cho thấy ảnh hưởng của sự cố đứt dây cáp dài (808, 818, 829, 839) đối với các cáp liền kề (809, 819, 830, 840) là rất lớn, lực căng trong cáp thay đổi từ (3207KN, 3766KN,3189KN, 3766KN) tới (4242KN, 5313KN,4238KN, 5340KN) tăng 32%, 41%, 33%, 42%. Như vậy nguy cơ gặp sự cố đứt các cáp liền kề là rất lớn so với các cáp còn lại. Từ hình 9, 17 và 22 cho thấy khi xảy ra đứt cáp dài phía giữa nhịp theo kịch bản đã trình bày ở trên tại vị trí giữa nhịp dầm có hiện tượng xoắn uốn kết hợp (chuyển vị theo thời gian của hai điểm trên mặt cắt ngang không đều nhau), tại vị trí nhịp biên không có xuất hiện dao động uốn xoắn kết hợp. Hình 10, 18 và 21 cho thấy khi đứt cáp chuyển vị theo phương dọc cầu bộ cáp giữa nhịp đứt sẽ ảnh hưởng nhiều đến chuyển vị trụ tháp hơn so với bộ cáp nhịp biên. Từ hình 12, 13, 14 cho thấy ảnh hưởng của cáp ngắn đứt là không đáng kể, ít ảnh hưởng đến các bộ phận của kết cấu. Từ hình 16 cho thấy ảnh hưởng của sự cố đứt 02 cặp cáp dài (808,809; 829, 830; 818,819; 839, 840) đối với các cáp liền kề (820, 841, 810, 831) là rất lớn, lực căng thay đổi từ (3140KN, 3139KN, 3395KN, 3395KN) tới (5364KN, 5575KN, 5867KN, 5930KN) tăng 69%, 78%, 73%, 75%. Như vậy nếu các lực trong cáp thiết kế bằng 45% lực tới hạn của bó cáp thì lực căng xuất hiện trong cáp sau khi đứt hai cáp bằng 80% lực tới hạn. Do đó, nguy cơ xảy ra đứt cáp liền kề là rất lớn. Từ hình 20 cho thấy ảnh hưởng của sự cố đứt 03 cặp cáp dài (808, 809, 810; 829, 830, 831; 818, 819, 820; 839, 840, 841) đối với các cáp liền kề (821, 842, 811, 832) là rất lớn, lực căng thay đổi từ (3102KN, 2995KN, 3016KN, 3016KN) tới (6637KN, 6839KN, 6715KN, 6475KN) tăng 114%, 128%, 123%, 115%. Như vậy nếu các lực trong cáp thiết kế bằng 45% lực tới hạn của bó cáp thì lực căng xuất hiện trong cáp sau khi đứt hai cáp bằng 97- 103% lực tới hạn. Do đó có nguy cơ một hiện tượng sụp đổ lan truyền sẽ xảy ra khi hai cáp dài bị đứt. Kết hợp với kết quả hình 23 cho thấy khi ba cáp dài phía giữa nhịp bị đứt nguy cơ xảy ra sụp đổ lan truyền rất lớn vì ngoài nguy cơ đứt thêm cáp kế tiếp thì dầm còn bị mất ổn định uốn ngang. 5. Kết luận Bài báo đã tiến hành phân tích kết cấu bằng mô hình phần tử hữu hạn phi tuyến, kết quả có độ tin cậy cao do đưa được vào kết quả ứng suất dư trong kết cấu khi chịu tải trước đó. Qua kết quả phân tích trên cho thấy các cáp liền kề với cáp bị đứt sẽ bị ảnh hưởng lớn hơn so với các cáp còn lại và các cáp dài bị đứt sẽ ảnh hưởng lớn đến phản ứng động lực học của kết cấu. Với mô hình các cáp KẾT CẤU - CÔNG NGHỆ XÂY DỰNG 30 Tạp chí KHCN Xây dựng - số 3/2019 đứt theo thời gian khác nhau cho thấy rõ hiện tượng dao động uốn xoắn xuất hiện trong dầm. Đối với cầu dây văng mặt cắt chữ (mặt cắt hở) sẽ gặp nguy hiểm khi đứt 2 cặp cáp dài và xảy ra sụp đổ lan truyền khi đứt 3 cặp cáp dài. TÀI LIỆU THAM KHẢO 1. PTI (2007). Recommendations for Stay Cable Design, Testing and Installation. Post Tension Institute. 2. Maren Wolff and Uwe Starossek (2009). Cable loss and progressive collapse in cable-stayed bridges. Bridge Structures Vol. 5, No. 1, March, 17–28. 3. M. Wolff and U. Starossek (2010). Cable-loss analyses and collapse behavior of cable-stayed bridges. IABMAS2010, The Fifth International Conference on Bridge Maintenance, Safety and Management, July 11-15, 2010, Philadelphia, USA. 4. Hyttinen, E. & Välimäki, J. & Järvenpää, E. (1994). Cable stayed bridges effect, of breaking of a cable. In Cable stayed and suspension bridges, Proceedings AFPC Conference, October 12-15, 1994. 5. Vu Hoang, Osamu Kiyomiya, Tongxiang An (2016). Experimental and dynamic response analysis of cable-stayed bridge due to sudden cable loss. Journal of Structural Engineering Vol.62A. 6. Nguyen Trong Nghia, Vanja Samec (2016). Cable- Stay Bridges-Investigation of Cable Rupture. Journal of Civil Engineering and Architecture 10, 270-279. 7. R. Dasa, A. D. Pandeyb, Soumyac, M. J. Maheshd, P. Sainie, and S. Anvesh (2016). Progressive Collapse of a Cable Stayed Bridge. Procedia Engineering 144, 132 – 139. 8. Harshil Jani1 and Dr. Jignesh Amin (2017). Analysis of cable stayed bridge under cable loss. International Journal of Bridge Engineering (IJBE), Vol. 5, No. 1, pp. 61-78. 9. Unified Facilities Criteria (UFC) (2016). Design of buildings to resist progressive collapse. November. 10. David N. Bilow, Mahmoud Kamara (2004). Progressive Collapse Design Guidelines Applied to Concrete Moment-Resisting Frame Buildings. ASCE Structures Congress. 11. Edward L. Wilson (2002). Three-Dimensional Static and Dynamic Analysis of Structures. Computers and Structures, Inc. Berkeley, California, USA. Ngày nhận bài: 17/6/2019. Ngày nhận bài sửa lần cuối: 04/7/2019. KẾT CẤU - CÔNG NGHỆ XÂY DỰNG Tạp chí KHCN Xây dựng - số 3/2019 31 ANALYSIS OF PROGRESSIVE COLLAPSE OF CABLE STAYED BRIDGE BY FINITE ELEMENT METHOD
File đính kèm:
 phan_tich_sup_do_lan_truyen_trong_cau_day_vang_bang_phuong_p.pdf
phan_tich_sup_do_lan_truyen_trong_cau_day_vang_bang_phuong_p.pdf

