Phân tích hóa lỏng đập vật liệu địa phương dưới tác dụng của tải trọng động

KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 1
PHÂN TÍCH HÓA LỎNG ĐẬP VẬT LIỆU ĐỊA PHƯƠNG 
DƯỚI TÁC DỤNG CỦA TẢI TRỌNG ĐỘNG 
Nguyễn Quang Hùng 
Trường Đại học Thủy lợi 
Tóm tắt: Hiện tượng hóa lỏng thường xảy ra đối với vật liệu rời là hiện tượng mà sức chịu tải của 
vật liệu bị giảm nhỏ cùng với sự gia tăng đột ngột áp lực nước lỗ rỗng do tác dụng của tải trọng 
động và đặc biệt là tải trọng do động đất gây ra với thời gian xảy ra rất nhanh. Hiện tượng này 
là một trong những hiện tượng phá hoại nguy hiểm nhất đối với đập vật liệu địa phương khi chịu 
tác động của tải trọng động. Bài báo này trình bày các cơ sở lý thuyết động lực học cũng như cách 
giải bài toán phi tuyến động lực đối với đập vật liệu địa phương nhằm xác định điều kiện hóa lỏng 
của đập vật liệu địa phương trên nền không phải là đá. 
Từ khóa: Đập vật liệu địa phương, ứng suất chính, áp lực nước lỗ rỗng, hóa lỏng 
Summary: Liquefaction phenomenon often occurs for loose materials is the phenomenon that the 
load capacity of the material is reduced with the sudden increase in pore water pressure due to 
the effect of dynamic loads and especially loads gravity caused by earthquakes with very fast time. 
This phenomenon is one of the most dangerous destructive phenomena for local dams when 
subjected to dynamic loads. This paper presents the dynamical theory bases as well as how to 
solve dynamic nonlinear problems for local material dams to determine the liquefaction conditions 
of local material dams on non-rock ground. 
Keywords: Embankment dam, Main stresses, Pore water pressure, Liquefaction 
1. ĐẶT VẤN ĐỀ* 
Đối với nền cũng như công trình vật liệu địa 
phương có đặc tính vật liệu rời chịu tác động 
của tải trọng động trong điều kiện không thoát 
nước làm cho áp lực nước lỗ rỗng ra tăng dẫn 
tới giảm nhỏ ứng suất hiệu quả. Điều này dẫn 
tới modul kháng cắt cũng như cường độ kháng 
cắt của vật liệu giảm nhỏ, nếu quá trình này này 
phát triển tới hạn áp lực nước lỗ rỗng phát triển 
bằng ứng suất tổng, ứng suất hiệu quả của vật 
liệu σ’ = 0 sẽ làm cho các hạt vật liệu không còn 
liên kết với các hạt xung quanh, lúc này vật liệu 
hoàn toàn không còn khả năng chịu lực dẫn tới 
hư hỏng nền cũng như công trình. Hiện tượng 
này được gọi là hóa lỏng. [1-2] Từ đó có thể 
thấy rằng việc nâng cao ứng suất hiệu quả trong 
vật liệu địa phương đồng nghĩa với việc giảm 
Ngày nhận bài: 08/4/2019 
Ngày thông qua phản biện: 28/5/2019 
thiểu khả năng xảy ra hóa lỏng. Một số hư hỏng 
đập vật liệu địa phương do hiện tượng hóa lỏng 
nền và đập có thể kể đến như đập Sheffield xảy 
ra năm 1925 với gia tốc nền 0.15g.[3]. Nội dung 
bài báo này trình bày các cơ sở lý thuyết động 
lực học cũng như cách giải bài toán phi tuyến 
động lực đối với đập vật liệu địa phương nhằm 
xác định điều kiện hóa lỏng của đập vật liệu địa 
phương trên nền không phải là đá. 
2. PHƯƠNG PHÁP NGHIÊN CỨU 
2.1. Phương trình cân bằng động và phương 
pháp giải 
(a ) Thiết lập phương trình cân bằng động 
Đối với vấn đề tính toán động, ngoài việc xem 
xét tác động của trọng lực đối với cốt đất, áp lực 
nước lỗ rỗng cũng như các loại tải trọng ngoài 
Ngày duyệt đăng: 10/6/2019 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 2
khác, vấn đề hết sức quan trọng cần được xem 
xét đến là lực quán tính và lực cản. Khi sử dụng 
phương pháp phần tử hữu hạn (FEM) để giải bài 
toán động, có thể từ điều kiện cân bằng nút để 
thiết lập nên hệ phương trình cân bằng của toàn 
hệ.từ véc tơ gia tốc động đất theo hai phương 
trọng lực và phương ngang
)}(),({)}({ twtutv ggg , khi đó véc tơ chuyển 
vị của chất điểm được định nghĩa )}(),({ twtu , 
vận tốc và gia tốc được định nghĩa: 
)}(),({)},(),({ twtutwtu . Khi đó véc tơ 
chuyển vị, vận tốc và gia tốc được định nghĩa là 
)}({)},({)},({ ttt  Khi đó phương trình cân 
bằng được thể hiện như sau: [4] 
)}(]{][[)}(]{[)}(]{[)}(]{[ tvGMtKtCtM g  （1） 
Trong đó: 
[M]-ma trận khối lượng； 
[C]-Ma trận cản tổng thể 
[K]-Ma trận cứng tổng thể. Trong đó:
GE )1(2  ，G là phi tuyến phụ thuộc vào 
biến dạng  
[G]-Ma trận chuyển trí，
010
001
.........
010
001
010
001
][G 
(b) Giải phương trình cân bằng động 
Giả thiết trong khoảng thời gian [( tt ), t ] gia 
tốc biến đổi theo quy luật tuyến tính. Khi đó ta 
có: 
t
tttttt

 )}{}({}{}{ 
)0( t  （2） 
Tích phân công thức (1) thu được vận tốc và 
chuyển vị tại thời điểm t như sau 
tttttt
tt
}{
2
}{
2
}{}{  
 (3) 
22 }{
6
1
}{
3
1
}{}{}{ tt ttttttttt    (4) 
Từ hai công thức (3) và (4). Sau khi biến đổi thu 
được: gia tốc tại thời điểm t:: 
tttt A
t
 }{}{
6
}{
2
 (5) 
Trong đó: 
tttttttt
tt
A 
 }{2}{
6
}{
6
}{
2
 (5a) 
Thay công thức (5) vào công thức (3) thu 
được: 
tttt B
t
 }{}{
3
}{  (6) 
Trong đó: 
 tttttttt
t
t
B 
 }{
2
}{2}{
3
}{  (6a) 
Thay công thức (5) và (6) vào công thức (1) thu 
được phương trình cân bằng: 
tt RK }{}}{{  (7) 
Trong đó: 
][
6
][
3
][}{
2
M
t
C
t
KK
 (7a) 
tttttt
AMBCRR
 }]{[}]{[}{}{ (7b) 
Nếu như tại thời điểm tt , các tham số đều 
đã biết, có thể sử dụng công thức (5a),(6a) thay 
vào công thức (7b) tìm được tR}{ ，từ đó dựa 
vào công thức (7) tìm ra được t}{ tại thời 
điểm tính toán t. 
2.2 Ma trận khối lượng, ma trận cản và ma 
trận cứng tổng thể 
(a) Ma trận khối lượng 
Ma trận khối lượng（Lumped Mass Matrix）
được xây dựng trên nguyên tắc coi gia tốc trong 
mỗi phần tử là như nhau, từ khối lượng phần tử 
được phân phối về các điểm nút, ma trân tập 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 3
hợp khối lượng các điểm nút này được gọi là 
ma trận khối lượng [M]。 
Ma trận khối lượng [M] được cho rằng có cùng 
quy luật phân phối với chuyển vị trong phần tử 
về các điểm nút. Chính vì vậy nên cách xây 
dựng ma trận khối lượng tổng thể [M] từ các ma 
trận khối lượng phần từ [m]e tương tự như đối 
với ma trận cứng tổng thể. 
(b) Ma trận cản [C]. 
Giả thiết lực cản cùng phương nhưng ngược 
chiều với chuyển động, khi đó ma trận cản phần 
tử được xác định như sau: [c]e=α[m]e . Với 
quan niệm là lực cản do nội ma sát sinh ra thì 
lực cản và tốc độ tiến dạng là tỷ lệ thuận với 
nhau , khi đó 
ee kc ][][  . Kết hợp cả hai điều 
này sẽ thu được : 
eee kmc ][][][  ，


 , 。 lực cản đơn vị phần tử，
không chỉ phụ thuộc vào đặc tính vật liệu của 
phần tử mà còn phụ thuộc vào ứng suất cắt của 
phần tử và có thể được xác định từ đường cong 
thực nghiệm 



~
max
. Để có thể xác định 
được giá trị max

, có thể sử dụng công thức 
kinh nghiệm của hardin và cộng sự như sau: 
[5] 
Bảng 1: Công thức kinh nghiệm xác định max 
Loại đất max （%） 
Cát khô max =33-1.5lgN 
Cát bão hòa max =28-1.5lgN 
Đất phù sa bão hòa Nfm lg5.17.0)(429
5.05.0
max  
Các loại đất có tính dính bão hòa Nff m lg5.15.1))(03.03(31
5.05.0
max  
N-Số chu kỳ thử nghiệm tải trọng động, đối với 
mặt cắt đáy đập có thể lựa chọn số lượng dao 
động tương ứng với gia tốc trung bình theo 
phương pháp lịch sử thời gian. 
f - tần số dao động tuần hoàn , đối với mặt cắt 
đáy đập có thể sử dụng tần số dao động trung 
bình tại vị trí xây dựng đập. 
m - Ứng suất hiệu quả trung bình（105Pa）
，Đối với nền đập 
zm
K
 
 )
3
21
( 0
，Đối 
với thân đập 3
321 
 m
. 
Trong quá trình tính toán, biến dạng cắt (tiếp 
tuyến) thay đổi dẫn tới lực cản cũng thay đổi 
theo, có thể sử dụng phương pháp lặp để tìm 
cực cản này. 
(c) Ma trận cứng tổng thể 
Ma trận cứng tổng thể trong bài toán động về 
hình thức tương tự như ma trận cứng tổng thể 
trong bài toán tĩnh, tuy nhiên giá trị modul E 
được thay thế bởi G)1(2  , trong đó G là giá 
trị phi tuyến tính. Khi sử dụng mô hình Hardin 
và Drnevic [5] có thể biểu diễn G dưới dạng 
sau: 
)]exp(1[1
1
max
rr
baG
G




 (8)
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 4
Bảng 2: Hệ số a,b 
Loại đất 
Modul cản tiếp tuyến 
(modul cắt) 
a b 
Cát khô eqG -0.5 0.16 
eq )1(60.0
6/1 N 12/11 N 
Cát bão hòa eqG -0.20lgN 0.16 
eq )90.0(54.0
6/1 N )1(65.0 12/1 N 
Đất dính 
bão hòa 
 1+0.25lgN 0.13 
 - Biến dạng cắt động. r - Biến dạng cắt 
max
max
G
r

 . maxG —
5.0
max,2max )( mKG  hoặc 
5.0
2
max )()(
1
)97.2(326
mOCR
e
e
G  
 （105Pa）
，e là độ rỗng，OCR là độ cố kết， là chỉ số 
dẻo, IP là tham số. 
Bảng 3: Quan hệ và IP 
IP 0 20 40 60 80 ≥100 
 0 0.18 0.30 0.41 0.48 0.50 
max,2K - được xác định bằng thí nghiệm trong 
phòng đối với bài toán biến dạng nhỏ. 
m - Ứng suất hiệu quả trung bình trạng thãi 
tĩnh. Đối với bài toán đập, giá trị này là ứng suất 
trung hiệu quả trung bình của phần tử tại trạng 
thái tĩnh. 
(d) Các nguyên nhân ảnh hưởng tới modul cắt G 
Khi thiết lập ma trận độ cứng phần tử ,việc lựa 
chọn giá trị G cần phải chú ý một số điểm sau: 
- Đối với đất có độ rỗng nhỏ và có hàm lượng 
sét cao, dưới tác động của tải trọng đông áp lực 
nước lỗ rỗng không phát triển nhiều ( m không 
thay đổi) nên dẫn tới giá trị maxG là hằng số. Do 
vậy nên G chỉ phụ thuộc vào biến dạng cắt  
mà thôi. 
- Đối với đất xốp không đủ độ chặt hoặc cát bão 
hòa không đủ độ chặt: Trong quá trình chịu tác 
động của tải trọng động, áp lực nước lỗ rỗng 
phát triển mạnh mẽ làm giảm sức chịu tải của 
cốt đất dẫn tới giá trị G giảm nhỏ, lúc này ngoài 
sự phụ thuộc vào biến dạng cắt  mà G còn phụ 
thuộc vào sự thay đổi của m . 
2.3. Phương pháp tính toán áp lực nước lỗ 
rỗng chịu tác dụng của tải trọng động 
(a) Phương pháp đường cong thực nghiệm 
Sự thay đổi ứng suất động (hoặc gia tốc động 
đất), số chu kỳ dao động, và độ cố Kc đều là 
những nguyên nhân quan trọng gây ra sự thay 
đổi áp lực nước lỗ rỗng trong quá trình chịu tải 
trọng động. Thông qua thí nghiệm rung động, 
dựa vào số chu kỳ dao động n đã thiết lập được 
quan hệ（
33
1 ~)(~)(




 dc
cf
df
d
u
K ）được 
thể hiện trên hình 1. 
Hình 1: Đường cong thực nghiệm xác định 
áp lực nước lỗ rỗng 
eqG
eq
5.020.01 f Nf mm lg3.025.2)exp(2.0 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 5
Bảng 4: Quan hệ số chu kỳ 
và thời gian dao động 
Cấp động neq t 
5.5～6 5 8 
6.5 8 14 
7.0 12 20 
7.5 20 40 
8.0 30 60 
Nếu gọi t là thời gian chịu tác dụng tải trọng 
động của công trình , neq là số dao động thì neq 
sẽ được xác định theo bảng 4. 
Chia nhỏ thời gian chịu tác động của tải trọng 
động thành các thời đoạn nhỏ )2~1( sT , số 
lần dao động của thời đoạn này là
T
t
n
n
eq
，như vậy số lần dao động được tính tích lũy từ 
các thời đoạn dao động
 
i
nn
1
 và thông 
thường trong tính toán , đối với mỗi thời đoạn 
dao động lại được chia nhỏ thành khoảng 100 
bước thời gian tính toán nhỏ với độ lớn 
st 02.0~01.0 . Do vậy trong một thời đoạn 
đoạn tính toán giải ra được ứng suất cắt tiếp 
tuyến tại các phần tử d . Dựa vào số dao động 
n tiến hành tra quan hệ
 3
~~

 dcd
u
K để tìm ra
3
du , từ đó tính ra được 
3
3 
 dd
u
u ，
dzym u )(
2
1
 。Sử dụng biến dạng 
cắt trung bình m đã biết của thời đoạn trước 
cũng như giá trị m của thời đoạn đang xét để 
tính toán được các giá trị modul G của phần tử 
và thiết lập ma trận cứng phần tử mới. Dựa vào 
bước thời gian t tiến hành tính toán phản ứng 
động trong thời đoạn này để tìm ra biến dạng 
cắt trung bình m và tính toán lại modul G. Tiến 
hành lặp lại quá trình này từ 2 đến 3 lần sẽ đạt 
được độ chính xác theo yêu cầu. Cuối cùng sử 
dụng các giá trị ứng suất cắt động và các 
nghiệm tìm được ở thời đoạn đang xét tiến hành 
tính toán tiếp cho thời đoạn tiếp theo. 
(b) Phương pháp công thức kinh nghiệm 
Phương pháp này cũng tương tự như phương 
pháp đường cong thực nghiệm, chia nhỏ thời 
gian chịu tác động của tải trọng động thành các 
thời đoạn T với số lần dao động trong thời 
đoạn là n . Khi đó áp lực nước lỗ rỗng tăng 
thêm trong thời đoạn T được xác định theo 
công thức sau: 
nnn
nnn
m
u l
ll
d 
 1
2
1
1
0 )/(
)/(1
)1( 
 
 
 (9)
0 - Ứng suất pháp cố kết động được xác định 
bằng thí nghiệm một trục hoặc ứng suất pháp cố 
kết động được xác định bằng thí nghiệm 3 trục 
khi
1
3
1 


cK . 
ln -Số lượng dao động cần thiết để hóa lỏng. 
Dựa vào tỷ lệ ứng suất cắt động của từng phần 
tử ,dựa vào điều kiện tỷ lệ 1 cK để tra ra số 
lượng dao động cần thiết để hóa lỏng； 
n- Thời gian tính toán dộngđược chia thành các 
thời đoạn n ， T
t
n
n
eq
 ； 
 -Tỷ lệ giữa ứng suất tiếp và ứng suất pháp. 
m- Tỷ lệ giảm áp lực nước lỗ rỗng được tra 
đường cong kinh nghiệm phụ thuộc vào α ( đối 
với cát m=1.1～1.3. 
 - Hệ số xác định theo thực nghiệm, thông 
thường đối với đất cát thường lựa chọn là 0.7. 
Dựa vào công thức (9) sẽ tính toán dược du 
tại thời đoạn j，Từ trường ứng suất tĩnh tổng 
ban đầu sau khi triệt tiêu áp lực nước lỗ rỗng 
 
j
du
1
thu được m . Dựa vào giá trị Gmax 
tính toán được và G có thể thiết lập được ma 
trận cứng tổng thể và giải bài toán phản ứng 
động. 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 6
2.4. Tiêu chuẩn hóa lỏng 
(a) Tiêu chuẩn 1 
Đối với thí nghiệm chấn động ba trục: 1
3

du : 
xảy ra hiện tượng hóa lỏng 
Đối với thí nghiệm cắt chấn động đơn: 1
0

du 
: xảy ra hiện tượng hóa lỏng 
Trong đó: ud : áp lực lỗ rỗng động 
σ3 : áp lực cố kết xung quanh của thí nghiệm. 
σ0 : áp lực cố kết trục đứng của thí nghiệm. 
(b) Tiêu chuẩn 2 
Trong thí nghiệm cắt tuần hoàn, khi biến dạng 
dọc trục (thí nghiệm chấn động 3 trục) hoặc 
biến dạng cắt (thí nghiệm cắt 1 trục) đạt đến 5% 
hoặc 10% , có thể cho là hóa lỏng. 
Dựa vào những định nghĩa trên đây về hóa lỏng, 
o đây o không thể gọi là hóa lỏng mà đúng hơn 
phải gọi là phá hoại . Thí nghiệm đã chứng 
minh, khi cK =σ1/σ3 ≤1.5, hai tiêu chuẩn trên 
đây về cơ bản là tương đồng. Trước khi xảy ra 
chấn động, khi hiệu số ứng suất chính trong 
đất tương đối lớn (các ứng suất chính khác biệt 
tương đối lớn) thì áp lực lỗ rỗng không đạt 
được 100% độ hóa lỏng. Tại đường biên của 
đập vật liệu địa phương, mặt nghiêng của đập 
(mái đập) cũng thuộc vào tình trạng này hình 
thức phá hoại hóa lỏng của đất cát bão hòa dưới 
mặt đất là đất cát sủi nước (nước bị ép ra ngoài) 
nhưng mái dốc hoặc nền đập không phải là hình 
thức này. Tuy nhiên mặt nền hoặc là than đập 
chỉ cần phát sinh 30~40% độ hóa lỏng, mái đập 
hoặc thân đập có thể phát sinh trượt ở quy mô 
lớn. Sở dĩ như vậy là vì khi đào mái đất nghiêng 
hoặc là thiết kế mái đập , nếu không xét đến áp 
lực lỗ rỗng chấn động, hệ số ổn định trong 
khoảng 1.3~1.4 thì khi phát sinh 30%-40% độ 
hóa lỏng, mái đập sẽ mất ổn định. 
(c) Tiêu chuẩn 3 
Lấy áp lực lỗ rỗng giới hạn của cân bằng cực 
hạn làm tiêu chuẩn, khi du đạt đến giá trị cru coi 
là hóa lỏng. 
Giá trị cru được tính như sau: 
d
ddd
cr
d
d
d
ddd
cr
d
d
u
u
 


 


sin2
)()(sin
sin
sin2
)()(sin
sin
313131
313131
(10) 
Trong đó: d là góc ma sát động, các kí hiệu 
khác như đã giải thích ở trên. 
Trong các tiêu chuẩn đã trình bày ở trên , cường 
độ chống cắt N tính được từ tiêu chuẩn 3 nhỏ 
hơn rất nhiều so với tiêu chuẩn 1 và tiêu chuẩn 2. 
Có thể nói rằng : cùng với 1 giá trị N , dùng tiêu 
chuẩn 3 thu được số lần chấn động đạt đến mức 
độ phá hoại là nhỏ nhất. Do vậy, vì tiêu chẩn hóa 
lỏng không thồng nhất, việc các định chính xác 
N là hết sức không hợp lý. 
3. KẾT QUẢ VÀ THẢO LUẬN 
3.1. Số liệu đầu vào 
Hình 2: Mặt cắt đập vật liệu địa phương 
dùng trong nghiên cứu 
Hình 3: lưới phần tử dùng trong tính toán 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 7
Ví dụ dùng để nghiên cứu ở đây là một đập vật 
liệu địa phương có mặt cắt ngang đập được cho 
ở hình 2 và các chỉ tiêu cơ lý của các loại vật 
liệu đắp đập và nền được cho ở bảng 2. Động 
đất dùng trong nghiên cứu là động đất cấp 8. 
Bảng 2: Chỉ tiêu cơ lý đập và nền 
TT Loại đất Ex=Ey (Mpa) µx=µy γ (KN/m3) kx=ky (10-7 m/s) 
1 Loại I 30 0.25 19.1 3 
2 Loại II 30 0.25 19.1 4.5 
3 Loại III 30 0.25 21.0 1 
4 Loại IV 30 0.25 21.0 1 
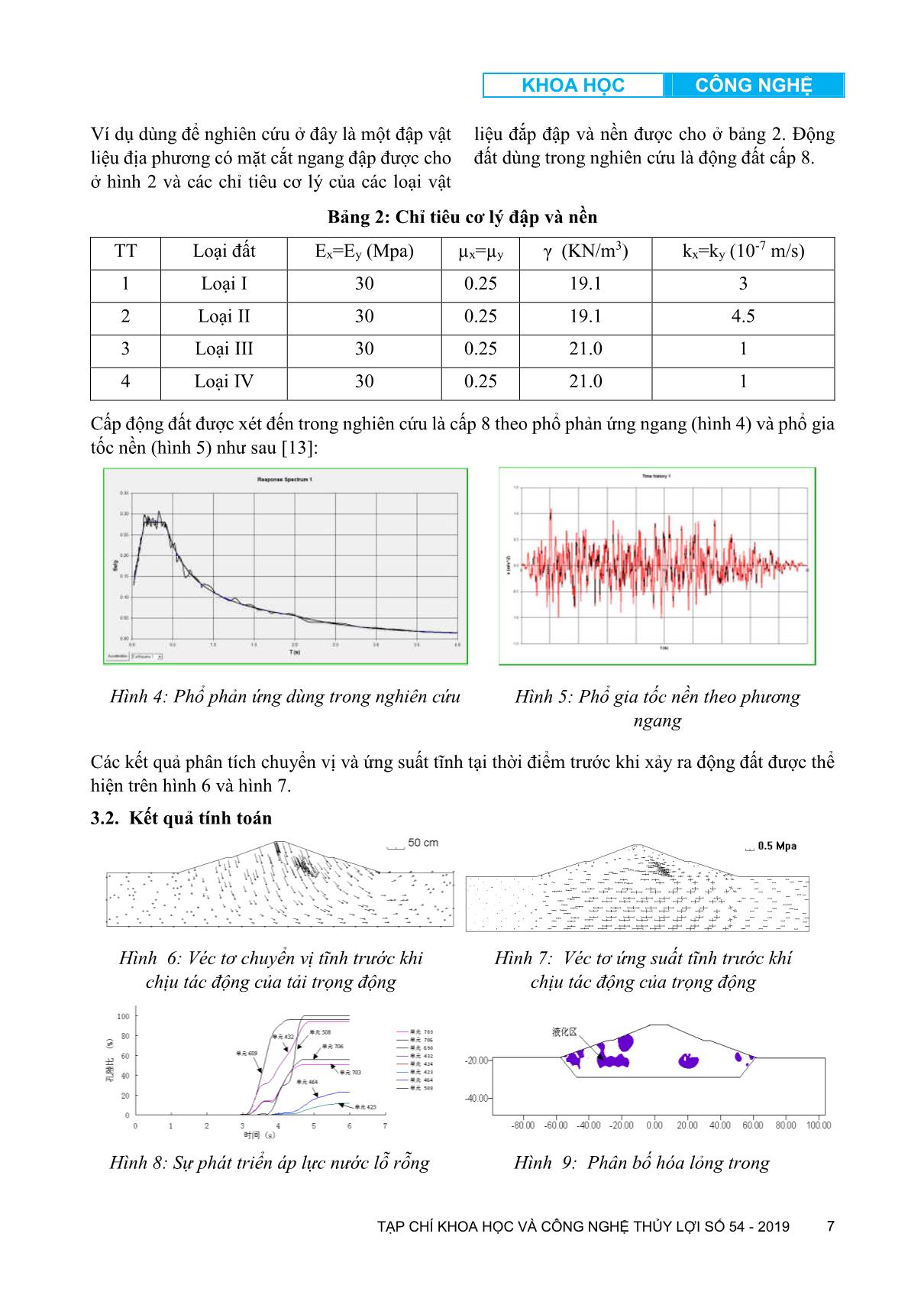
Cấp động đất được xét đến trong nghiên cứu là cấp 8 theo phổ phản ứng ngang (hình 4) và phổ gia 
tốc nền (hình 5) như sau [13]: 
Hình 4: Phổ phản ứng dùng trong nghiên cứu Hình 5: Phổ gia tốc nền theo phương 
ngang 
Các kết quả phân tích chuyển vị và ứng suất tĩnh tại thời điểm trước khi xảy ra động đất được thể 
hiện trên hình 6 và hình 7. 
3.2. Kết quả tính toán 
Hình 6: Véc tơ chuyển vị tĩnh trước khi 
chịu tác động của tải trọng động 
Hình 7: Véc tơ ứng suất tĩnh trước khí 
chịu tác động của trọng động 
Hình 8: Sự phát triển áp lực nước lỗ rỗng Hình 9: Phân bố hóa lỏng trong 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 54 - 2019 8
 tại một số phần tử thân đập và nền 
Hình 8 và hình 9 thể hiện quá trình phát triển áp 
lực nước lỗ rỗng tại một số vị trí trong thân đập 
cũng như sự xuất hiện các vùng hóa lỏng trong 
thân đập và nền. Những kết quả này cũng thể 
hiện tình hình chịu lực của đập vật liệu địa 
phương dưới tác dụng của tải trọng động. Phân 
bố vùng hóa lỏng xảy ra trong thân đập dưới 
tác dụng của động đất cho thấy rõ trạng thái 
phá hoại của đập cũng như sự phát sinh những 
vùng nguy hiểm trong thân đập nghiên cứu khi 
chịu tác dụng của tải trọng động. 
4. KẾT LUẬN 
Dựa trên phương trình cân bằng động, bài báo 
đã xây dựng phương pháp giải cũng như cách 
xác định các thành phần ma trận cản, ma trận 
khối lượng, ma trận cứng tổng thể cũng như các 
bước giải bài toán dao động đối với đập vật liệu 
địa phương. Bên cạnh đó, nội dung nghiên cứu 
cũng đưa ra tiêu chuẩn về hóa lỏng là một trong 
những tiêu chuẩn phá hoại chưa được đề cập 
đến trong các hệ thống tiêu chuẩn kỹ thuật xây 
dựng đập ở Việt Nam. Thông qua một ví dụ tính 
toán minh chứng về đập vật liệu địa phương với 
chuẩn phá hoại hóa lỏng, kết quả nghiên cứu đã 
cho thấy một bức tranh tương đối rõ nét về về 
hoại đập vật liệu địa phương dưới tác dụng của 
tải trọng động. 
TÀI LIỆU THAM KHẢO 
[1] Kramer, S.L.. Geotechnical Earthquake Engineering, Prentice Hall. 1996 
[2] Robert D. Holtz, William D. Kovacs .An Introduction to Geotechnical Engineering. 
Prentice-Hall, 1981 
[3] Seed H B and Lee K L. Liquefaction of Saturated Sands During Cyclic Loading. Proc. 
ASCE. J. SMFD. 1966. 92(SM6): 105~134 
[4] Nguyen Quang Hung ，Fu Shao Jun, Chen Sheng Hong. Study on adaptive time step of 
consolidation geotechnical problems by finite element method. China rock and soil 
mechanics. Vol 26/4. 591-595. 2005 
[5] Hardin và Drnevic. Shear Modulus and Damping in Soils: Design Equations and Curves. 
Geotechnical Special Publication 98(118) · January 1972 
[6] Nguyen Quang Hung. FEM of Geochnical Structures. Wuhan University. 2004