Phân tích giới hạn tấm dày 5 bậc tự do sử dụng phương pháp không lưới Element Free Galerkin (EFG)

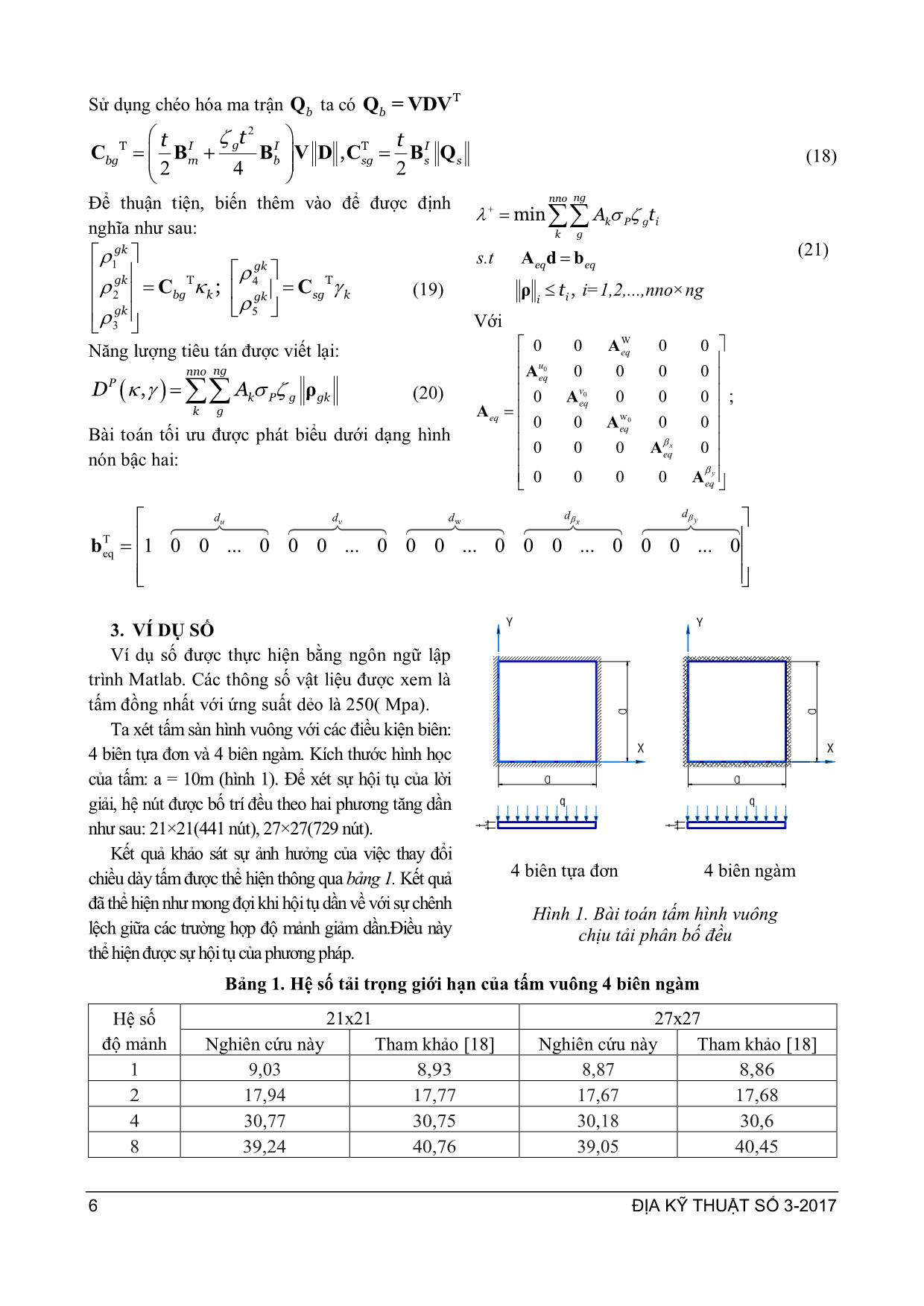
ĐỊA KỸ THUẬT SỐ 3-2017 3 
PHÂN TÍCH GIỚI HẠN TẤM DÀY 5 BẬC TỰ DO 
SỬ DỤNG PHƯƠNG PHÁP KHÔNG LƯỚI 
ELEMENT FREE GALERKIN (EFG) 
NGUYỄN NGỌC PHÚC*, NGUYỄN HOÀNG PHƢƠNG **, 
HỒ THỊ ĐOAN TRANG * 
The critical state of thick-plate using stabilized mesh-free method as a 
five-node plate bending element based on mindlin/reissener plate theory- 
element free galerkin (efg) 
Abstract: This papers concern about critical state of thick-plate using 
Stabilized Mesh-Free Method as a five-node plate bending element based 
on Mindlin/Reissener plate theory. Two case studies rectangular plates 
with lean and rigid boundary condition were considered. The result shows 
main failure forms by critical state which we want to know when using as 
mat, diaphragm wall, retaining wall, 
Keywords: Thick-plate; Stabilized Mesh-Free Method; Mindlin/Reissener 
plate theory; phần tử 5 bậc tự do; định lý cận trên. 
1. GIỚI THIỆU * 
Trong những thập niên gần đây việc xác 
định tải trọng giới hạn của công trình ngày càng 
đƣợc quan tâm L thuyết phân tích giới hạn 
ngày càng phát triển phù hợp với các l thuyết 
tấm khác nhau Trong phân tích giới hạn trƣờng 
chuyển vị hoặc trƣờng ứng suất sẽ đƣợc rời rạc 
sau đó định l cận trên hoặc định l cận dƣới 
đƣợc áp dụng để xác định tải trọng giới hạn 
Bên cạnh đó các phƣơng pháp số cũng 
không ngừng đƣợc phát triển và là 
công cụ đắc lực để nâng cao hiệu quả tính toán 
Một lớp phƣơng pháp số mới đƣợc phát triển 
trong thời gian gần đây là phƣơng pháp không 
lƣới (meshfree hay meshless) Gần đây nhiều 
phƣơng pháp không lƣới đƣợc phát triển nhƣ 
phƣơng pháp không lƣới Element Free Galerkin 
(EFG) không lƣới Local Petrov Galerkin 
(MLPG) không lƣới Radial Point Interpolation 
Method (RPIM) không lƣới Local Radial Point 
Interpolation Method (LRPIM) không lƣới 
* Khoa Xây dựng, Cao đẳng Xây dựng 2 
** Khoa Kiến trúc-Xây Dựng - Mỹ Thuật Ứng dụng, 
Đại Học Nguyễn Tất Thành 
Moving Kriging (MGK) Khác nhau cơ bản 
giữa các phƣơng pháp này là kỹ thuật nội suy 
có nhiều kỹ thuật nội suy đƣợc áp dụng nhƣ 
Kernel Partical Method, Moving Least Square 
Approximate, Partition of Unity, Kringing 
Interpolation 
Phƣơng pháp EFG là một phƣơng pháp 
không lƣới đƣợc phát triển bởi Belytchko et al., 
1994 Trong phƣơng pháp EFG xấp xỉ bình 
phƣơng cực tiểu MLS (Moving Least Square) 
đƣợc sử dụng để xây dựng hàm dạng phƣơng 
trình hệ thống đƣợc xây dựng thông qua dạng 
yếu Galerkin những ô nền đƣợc yêu cầu cho 
việc tính tích phân từng phần Khi sử dụng 
phƣơng pháp EFG để rời rạc trƣờng chuyển vị 
cho bài toán cận trên số lƣợng biến trong bài 
toán ít hơn nhiều so với khi rời rạc bằng FEM vì 
phƣơng pháp EFG chỉ yêu cầu một bậc tự do tại 
mỗi nút thay vì các bậc tự do của điểm Guass 
trong FEM Để đảm bảo tính chính xác cho lời 
giải khi sử dụng phƣơng pháp EFG tích phân 
nút ổn định (Stablised Confroming Nodal 
Intergration (SCNI)) đƣợc áp dụng để làm trơn 
biến dạng Khi đó tích phân đƣợc tính trực tiếp 
 ĐỊA KỸ THUẬT SỐ 3-2017 4 
tại các nút mà không sử dụng những điểm 
Gauss giúp giảm nhẹ chi phí tính toán 
Trong bài báo này phần tử EFG cho nút 5 
bậc tự do cho một nút đƣợc sử dụng Kết quả 
đạt đƣợc có cải thiện so với các phƣơng pháp 
khác sử dụng cho nút 3 bậc tự do 
2. CƠ SỞ LÝ THUYẾT 
2.1. Lý thuyết tấm Mindlin 5 bậc tự do 
L thuyết cắt bậc nhất (L thuyết tấm dày 
Mindlin-Reissner): 
Cùng xem xét miền thể tích trong 
2
R với 
mặt phẳng giữa tấm (mặt trung bình) 
Trƣờng chuyển vị theo l thuyết FSDT [5] 
gồm 5 bậc tự do nhƣ sau: 
0
0
0


, , , ,
, , , ,
, , ,
x
y
u x y z u x y z x y
v x y z v x y z x y
w x y z w x y
(
1) 
Biến dạng trong mặt phẳng đƣợc biểu hiện 
theo công thức 
0
   ε κ 
T
xx yy xy z (2) 
Với biến dạng màng và biến dạng cong 
0 0
 ε us 
 
1
2
  κ β βT 
(3) 
(4) 
Biến dạng cắt 
  ε βs w (5) 
2.2. Phƣơng pháp EFG 
Phƣơng pháp làm trơn biến dạng lần đầu tiên 
đƣợc trình bày bởi Chen et al (2000) và đƣợc 
hiệu chỉnh bằng cách sử dụng phép tích phân 
nút bởi Chen et al (2001): 
 φ , dΩ

h h
ij J ij J
J
ε x ε x x x x
(
6) 
trong đó hijε là giá trị đƣợc làm trơn của 
h
ijε 
tại nút J và υ là hàm phân phối (hàm trơn) và 
phải thỏa mãn những điểm sau (Chen et al 
2000; You et al., 2004): 
φ 0 φdΩ 1

J
vaø 
(7) 
Để đơn giản hàm υ đƣợc giả sử là những 
hàm nhỏ không đổi: 
1
, 
aφ , 
0, 
  
  
J
JJ
J
x
x x x
x
 (8) 
trong đó aJ là diện tích miền đại diện của nút J 
Thay phƣơng trình (8) vào (6) và áp dụng 
định l phân kì ta đƣợc: 
, ,
Ω
Γ
1 1
dΩ
2
1
 = d
2
J
J
h h h
ij J i j j i
J
h h
i j j i
J
u u
a
u n u n
a
 
ε x
(9) 
trong đó ΓJ là biên của miền Ω 
Với xấp xỉ bình phƣơng cực tiểu của trƣờng 
chuyển vị dạng trơn của biến dạng có thể đƣa ra 
nhƣ sau: 
ε x
x ε x x
ε x
h
xx J
h h h
J yy J m b J s
h
xy J
z 
ε B B d; B d (10) 
trong đó: T
1 1 1 1 1,..., , ,..., , ,..., , ,..., , ,..., n n n x xn y ynu u v v