Phân tích động học hệ ổn định đường ngắm

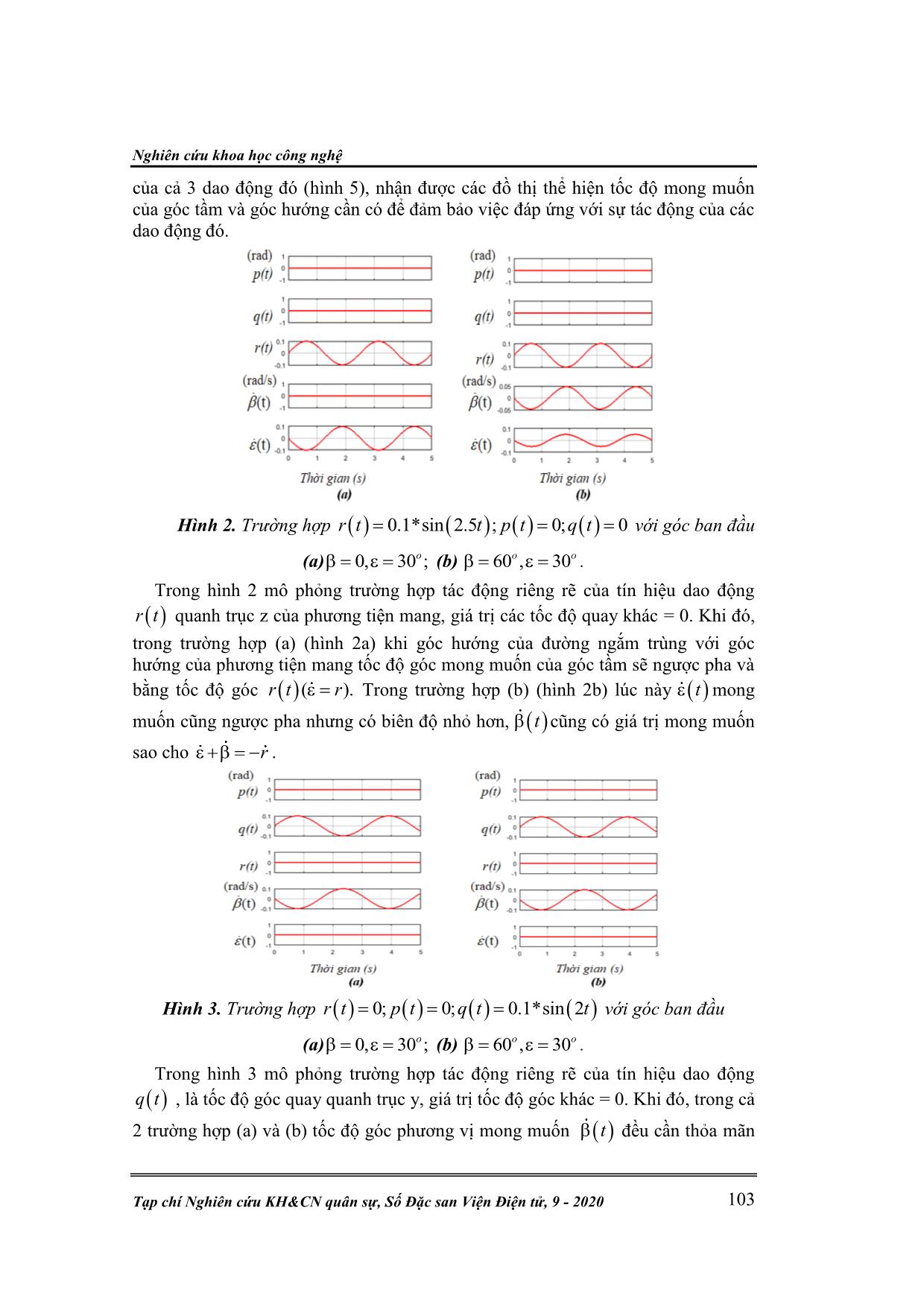
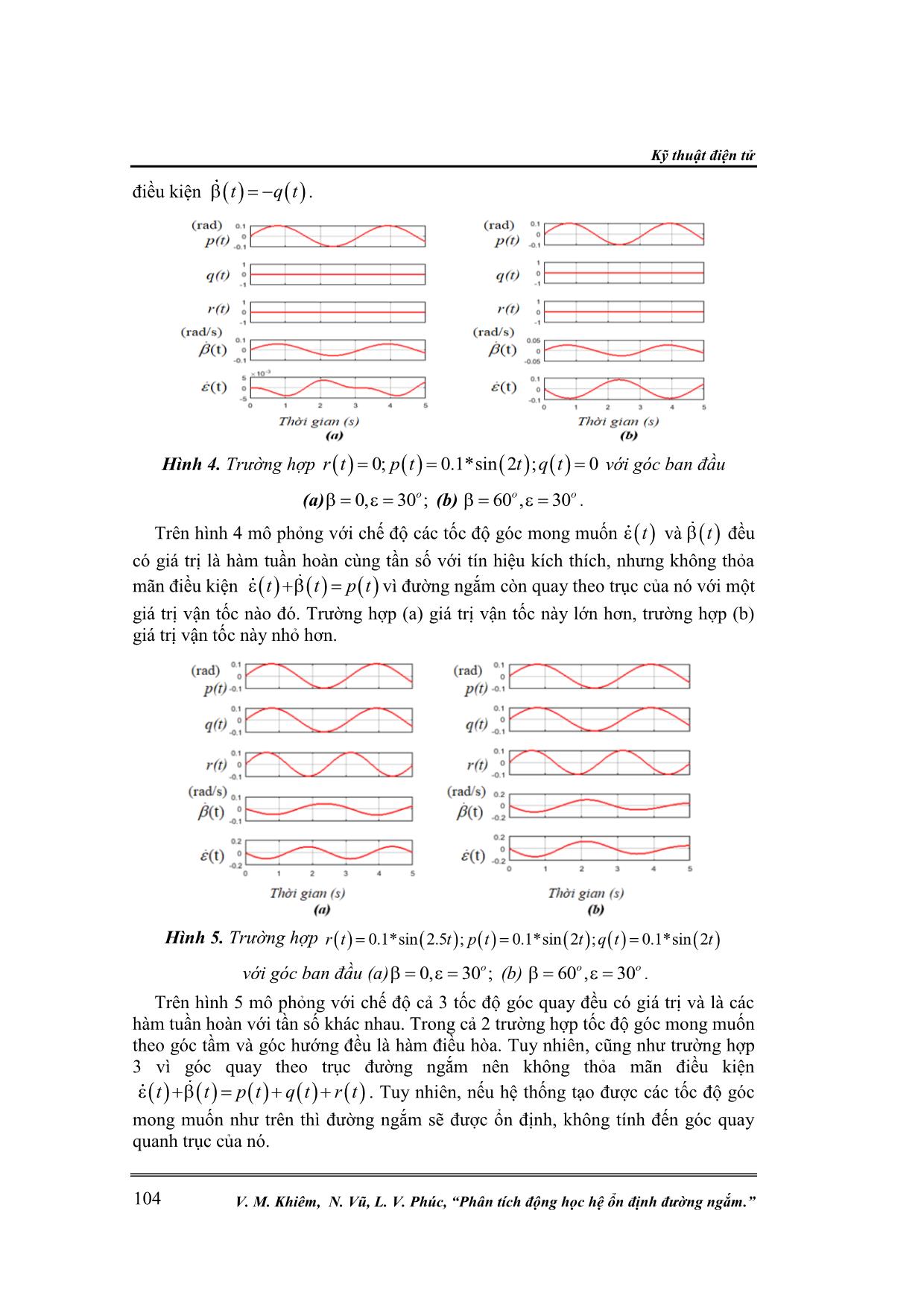
Kỹ thuật điện tử 
V. M. Khiêm, N. Vũ, L. V. Phúc, “Phân tích động học hệ ổn định đường ngắm.” 98 
PHÂN TÍCH ĐỘNG HỌC HỆ ỔN ĐỊNH ĐƯỜNG NGẮM 
Vũ Minh Khiêm1*, Nguyễn Vũ2, Lê Văn Phúc1 
Tóm tắt: Các hệ thống ổn định đường ngắm được sử dụng rộng rãi trong các hệ 
thống ra đa, anten vệ tinh và các hệ thống ngắm bắn trên các phượng tiện cơ động. 
Việc xây dựng hệ thống ổn định đường ngắm cần dựa trên động học của hệ thống. 
Báo cáo đề cập đến việc xây dựng các phương trình hình học và động học cho hệ 
thống ổn định đường ngắm 3 trục làm cơ sở tổng hợp hệ thống điều khiển. 
Từ khóa: Ổn định đường ngắm; Động học hệ gimbal; Mô hình động học 2D hệ gimbal. 
1. MỞ ĐẦU 
Trong các hệ thống trinh sát, phát hiện mục tiêu, điều khiển hỏa lực hay thông 
tin vệ tinh trên các phương tiện cơ động, hệ thống ổn định đường ngắm cho phép 
quan sát, bám sát mục tiêu cũng như tiêu diệt mục tiêu từ cự ly xa [1], hay đảm bảo 
chất lượng cho các hệ thống rada, laser hay thông tin vệ tinh [2]. Để điều khiển và 
ổn định đường ngắm cho các hệ thống quang học, một vài dạng gimbal tích hợp 
cùng các cảm biến quán tính được đề xuất [3]. Để thực hiện chức năng ổn định 
đường ngắm, thông thường hệ thống với gimbal 2 trục được sử dụng, trong đó, các 
cảm biến quán tính được đặt trong gimbal bên trong. Hai cảm biến tốc độ gyro 
được đặt trong gimbal để đo tốc độ góc của gimbal, cũng là tốc độ góc của đường 
ngắm trong không gian quán tính. Tín hiệu ra của gyro này được sử dụng để ổn 
định đường ngắm. Đây là phương pháp thông dụng và tiện lợi, nhưng do hạn chế 
về không gian nên các cảm biến gyro đo tốc độ góc bố trí trên gimbal thường là 
loại nhỏ, độ chính xác không cao. Để nâng cao chất lượng điều khiển, có thể trích 
tín hiệu từ các hệ thống dẫn đường độ chính xác cao, hay các cảm biến gyro có độ 
chính xác cao đặt trên phương tiện cơ động. Dưới đây sẽ trình bày động hình học 
của gimbal và phương pháp lấy tín hiệu từ cảm biến đặt trên phương tiện cơ động 
để điều khiển gimbal bảo đảm ổn định đường ngắm. 
2. ĐỘNG HÌNH HỌC CỦA HỆ GIMBAL 
Xem xét động hình học của hệ gimbal 2 trục, 1 trục hướng và 1 trục tầm. Để 
tính toán động hình học cho hệ gimbal này, dưới đây sẽ sử dụng hệ tọa độ sau: Hệ 
tọa độ quán tính I, hệ tọa độ gắn liền B, là hệ tọa độ gắn liền với phương tiện mang 
mà đế của bệ gimbal gắn chặt lên. Vì hệ gimbal có 2 trục nên dưới đây sẽ gọi là hệ 
pan-tilt. 
Hệ tọa độ Y gắn liền với trục phương vị và hệ tọa độ P gắn liền với trục tầm 
của hệ Pan-Tilt. Các hệ tọa độ liên kết với nhau như sau: Hệ tọa độ Y nhận được 
bằng cách quay hệ tọa độ B một góc β xung quanh trục Y (trục đứng), hệ tọa độ 
P nhận được bằng cách quay hệ tọa độ Y 1 góc ε quanh trục Z, hướng cần ổn 
định là trục OX. 
Các ma trận quay tương ứng với các hệ tọa độ và các phép quay trên như sau: 
0
0 1 0
0
Y
B
C S
C
S C
 
 
 (1) 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 99 
0
0
0 0 1
P
Y
C S
C S C
 
 
 (2) 
Trong đó, , , ,SC S C    ký hiệu thứ tự là cos ,sin ,cos ,sin    ; 
Y
BC ,
P
YC là ma 
trận quay từ hệ tọa độ B sang hệ tọa độ Y, và từ hệ tọa độ Y sang hệ tọa độ P. 
Trong bài toán ổn định thì các góc Ơle của hệ tọa độ B so với hệ tọa độ I không 
cần đưa vào. Tuy nhiên, các góc này phải đưa vào trong bài toán định vị. 
Giả sử trên phương tiện mang có các cảm biến gyro và đo được tốc độ góc của 
các trục của hệ tọa độ B so với hệ tọa độ quán tính I. 
 
TB
IB p q r (3) 
Ở đây, B
IB là tốc độ góc quay quán tính của hệ tọa độ B đo bởi hệ cảm biến 
quán tính gắn liền với hệ tọa độ B; p, q, r thứ tự là tốc độ góc của các trục x,y,z 
Tốc độ góc quán tính của hệ tọa độ Y đặt trong chính hệ đó ( Y
IY ) được xác định 
như sau: 
Y Y Y
IY IB BY   (4) 
Ở đó, Y
IB là tốc độ góc quán tính của hệ tọa độ B được đặt trong hệ tọa độ Y,
Y
BY là tốc độ góc của hệ tọa độ Y so với hệ tọa độ B và được đặt trong hệ tọa độ Y. 
Như vậy, ta có được: 
.Y Y BIB B IB
pC rS
C q
pS rC
 
 
  
 (5) 
0
0
Y
BY
  
 (6) 
Đặt (5) và (6) vào (4) nhận được: 
Y
Y
IY Y
Y
pC rS p
q q
pS rC r
 
 
   
 (7) 
Tốc độ góc quán tính của hệ tọa độ P đặt trong chính hệ đó được xác định như sau: 
P P Y
IP IY YP   (8) 
Với P
IP là tốc độ góc quán tính của hệ tọa độ Y được đặt trong hệ tọa độ P, 
P
YP là tốc độ góc của hệ P so với hệ Yvà được đặt trong hệ tọa độ P. 
Làm các phép triển khai các thành phần tương tự như (5) và (6) nhận được 
Kỹ thuật điện tử 
V. M. Khiêm, N. Vũ, L. V. Phúc, “Phân tích động học hệ ổn định đường ngắm.” 100 
Y Y P
P
IP Y Y P
Y P
p C q S p
q C p S q
r r
 
 
  
  
 (9) 
Đặt Yp Yq Yr trong (7) vào (9) nhận được: 
 PIP
C pC rS S q
C q S pC rS
pS rC
   
   
 
 
   
 
 (10) 
Để đường ngắm ổn định, không tính đến độ nghiêng của khung hình, điều kiện 
cần và đủ là: 
0
0
P
P
IP
p 
  
 (11) 
hay: 
pS rC
S pC rS qC
C
 
   

  
 
 (12) 
Biểu thức (12) cho thấy, khi  →±
2
 thì để ổn định đường ngắm, tốc độ góc của 
hệ tọa độ Y sẽ tiến tới ∞. Hệ thống tiến đến điểm kỳ dị. Đây là lý do trong một số 
trường hợp hệ Pan-Tilt không sử dụng để ổn định đường ngắm được, mà phải sử 
dụng hệ gimbal có số bậc tự do cao hơn. Tuy nhiên, vấn đề này sẽ không đề cập 
trong bài báo này. 
Giả sử  đủ nhỏ để hệ (12) không suy biến, khi đó các giá trị  , chính là các 
giá trị đặt: 
d
d
pS rC
S pC rS qC
C
 
   

  
 
 (13) 
Các giá trị này hoàn toàn được xác định khi các hệ truyền động đều có các cảm 
biến đo góc. 
3. ĐỘNG HỌC CỦA HỆ PAN-TILT 
Xem xét hệ thống như là vật cứng tuyệt đối với các trục gắn liền là x,y,z. Giả sử 
vật thể có mô men quán tính J và quay trong hệ tọa độ quán tính với tốc độ góc ω, 
khi đó [4]: 
 .H J  (14) 
.
dH
T H
dt
  (15) 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 101 
Với H là mô men quay của hệ; 
 T là tổng mô men bên ngoài tác động vào hệ. 
Áp dụng (14) và (15) cho các kênh tầm và kênh hướng của hệ Pan-Tilt. 
3.1. Đối với kênh tầm 
Mômen quay của kênh tầm: 
.p
. .q
.r
Px P
P
P P IP Py P
Pz P
J
H J J
J
  
 (16) 
Ở đây, P Px Py PzH diag J J J . 
Và phương trình động học kênh tầm được viết dưới dạng 
PP
IP P
dH
T H
dt
  (17) 
Do kênh tầm chỉ quay quanh trục Z nên phương trình (17) chỉ viết cho trục Z: 
 qp Pz P Py Px P PT J r J J p (18) 
Trong trường hợp hệ được thiết kế đối xứng 
Py PxJ J , khi đó, (18) trở thành: 
.p Pz PT J r 
 (19) 
Với Pr xác định trong (10) ở dạng: 
Pr pS rC   (20) 
Lấy đạo hàm Pr từ (20) ta nhận được: 
S CPr p pC r rS       
 (21) 
Đặt (21) vào (19) ta nhận được: 
 p PzT J p r S p r C     (22) 
Có thể viết lại thành: Pz p YBJ T T 
(23) 
Với YBT r p S p r C    (24) 
Là ảnh hưởng của chuyển động trong hệ tọa độ B và Y tới hệ tọa độ P. 
3.2. Đối với kênh hướng 
Mômen quay của kênh hướng được xác định như sau: 
T
Y P P
Y Y YP Y p IPH J C J   
p pp 0 p
q 0 q
r 0 0 1 r
Yx Y Px Y Y Py Y Y
Yx Y Px P
Yy Y Py P Yy Y Py Y Y Px Y Y
Yz Y Pz P
Yz Y Pz Y
J C J C q S S J q C p SJ C S J
J S C J J q C J q C p S S J p C q S
J J J r J r
     
 
       
  
 (25) 
Kỹ thuật điện tử 
V. M. Khiêm, N. Vũ, L. V. Phúc, “Phân tích động học hệ ổn định đường ngắm.” 102 
Ở đó, thành phần thứ hai của phương trình (25) là mô men quay (mô men động 
lượng) của hệ góc tầm (Pitch gimbal) chuyển tới hệ góc hướng. 
Phương trình mômen của hệ góc hướng sẽ là: 
.YYY IY Y
dH
T H
dt
  (26) 
Do hệ hướng chỉ quay xung quanh trục Y nên phương trình mô men (26) của 
trục này căn cứ vào (25) và (7) sẽ là: 
 2 2 qY Yy Y Py Px yT J q J C J S  
 2 2Yy Py Px PBT J C J S T   (27) 
Với PBT là ảnh hưởng của chuyển động của hệ tọa độ B và P tới hệ tọa độ Y. 
 Khi đó, ta được Yy Py Y PBJ J T T  . (28) 
4. MÔ PHỎNG XÁC ĐỊNH TỐC ĐỘ GÓC MONG MUỐN 
Để mô phỏng, đặt tốc độ góc của phương tiện mang:  p q r . 
Với 0.1sin(2 ); 0.1sin(2 ); 0.1sin(2.5 )p t t q t t r t t . 
Quá trình mô phỏng thử nghiệm các tín hiệu dao động trong các trường hợp có 
góc tầm 30o và góc hướng tại các điểm 0o và 60 .o 
Mô phỏng để xác định tốc độ góc tầm và góc hướng ,d d  theo thời gian, 
với giả thiết hệ thống điều khiển đảm bảo cho hệ thống luôn ổn định theo đúng 
giá trị đặt. 
Sơ đồ khối hệ thống mô phỏng trên Simulink: 
Hình 1. Sơ đồ khối hệ thống mô phỏng. 
Trước hết, đặt các tín hiệu dao động của phương tiện mang riêng rẽ theo từng 
kênh dao động , ,pr t q t t (hình 2, hình 3, hình 4) và mô phỏng sự tác động 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 103 
của cả 3 dao động đó (hình 5), nhận được các đồ thị thể hiện tốc độ mong muốn 
của góc tầm và góc hướng cần có để đảm bảo việc đáp ứng với sự tác động của các 
dao động đó. 
Hình 2. Trường hợp 0.1*sin 2.5 ; 0; 0r t t p t q t với góc ban đầu 
(a) 0, 30 ;o  (b) 60 , 30o o  . 
Trong hình 2 mô phỏng trường hợp tác động riêng rẽ của tín hiệu dao động 
 r t quanh trục z của phương tiện mang, giá trị các tốc độ quay khác = 0. Khi đó, 
trong trường hợp (a) (hình 2a) khi góc hướng của đường ngắm trùng với góc 
hướng của phương tiện mang tốc độ góc mong muốn của góc tầm sẽ ngược pha và 
bằng tốc độ góc ( ).r t r Trong trường hợp (b) (hình 2b) lúc này t mong 
muốn cũng ngược pha nhưng có biên độ nhỏ hơn, t cũng có giá trị mong muốn 
sao cho r  . 
Hình 3. Trường hợp 0; 0; 0.1*sin 2r t p t q t t với góc ban đầu 
(a) 0, 30 ;o  (b) 60 , 30o o  . 
Trong hình 3 mô phỏng trường hợp tác động riêng rẽ của tín hiệu dao động 
 q t , là tốc độ góc quay quanh trục y, giá trị tốc độ góc khác = 0. Khi đó, trong cả 
2 trường hợp (a) và (b) tốc độ góc phương vị mong muốn t đều cần thỏa mãn 
Kỹ thuật điện tử 
V. M. Khiêm, N. Vũ, L. V. Phúc, “Phân tích động học hệ ổn định đường ngắm.” 104 
điều kiện t q t . 
Hình 4. Trường hợp 0; 0.1*sin 2 ; 0r t p t t q t với góc ban đầu 
(a) 0, 30 ;o  (b) 60 , 30o o  . 
Trên hình 4 mô phỏng với chế độ các tốc độ góc mong muốn t và t đều 
có giá trị là hàm tuần hoàn cùng tần số với tín hiệu kích thích, nhưng không thỏa 
mãn điều kiện t t p t  vì đường ngắm còn quay theo trục của nó với một 
giá trị vận tốc nào đó. Trường hợp (a) giá trị vận tốc này lớn hơn, trường hợp (b) 
giá trị vận tốc này nhỏ hơn. 
Hình 5. Trường hợp 0.1*sin 2.5 ; 0.1*sin 2 ; 0.1*sin 2r t t p t t q t t 
 với góc ban đầu (a) 0, 30 ;o  (b) 60 , 30o o  . 
Trên hình 5 mô phỏng với chế độ cả 3 tốc độ góc quay đều có giá trị và là các 
hàm tuần hoàn với tần số khác nhau. Trong cả 2 trường hợp tốc độ góc mong muốn 
theo góc tầm và góc hướng đều là hàm điều hòa. Tuy nhiên, cũng như trường hợp 
3 vì góc quay theo trục đường ngắm nên không thỏa mãn điều kiện 
 t t p t q t r t  . Tuy nhiên, nếu hệ thống tạo được các tốc độ góc 
mong muốn như trên thì đường ngắm sẽ được ổn định, không tính đến góc quay 
quanh trục của nó. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 105 
5. KẾT LUẬN 
Hệ thống Pan-Tilt với cảm biến tốc độ góc đặt trên bệ cố định, hoàn toàn có khả 
năng cung cấp thông tin đầy đủ để hệ thống tự động điều khiển hoạt động, đảm bảo 
ổn định đường ngắm. Tuy nhiên, khi có sai số điều khiển, giá trị các góc của 
đường ngắm trong không gian quán tính sẽ trôi khỏi điểm ban đầu. Điều này đặt ra 
vấn đề bổ sung thêm các cảm biến để có thể xác định được độ trôi của đường 
ngắm, làm cơ sở thiết kế hệ thống ổn định hoạt động trong thời gian dài. Ngoài ra, 
khi góc tầm quá cao, hệ thống rơi vào điểm kỳ dị, mất khả năng điều khiển. Điều 
này đặt ra yêu cầu nghiên cứu bổ sung thêm một bậc tự do cho hệ thống gimbal 
đảm bảo khả năng hoạt động của hệ thống ổn định trong mọi điều kiện. Các vấn đề 
này cần được tiếp tục nghiên cứu và giải quyết. 
TÀI LIỆU THAM KHẢO 
[1]. 
J.M. Hilkert, “Stabilization, Pointing and Tracking System Technology 
Handbook”, Texas Instrument Incorporated, May 1991. 
[2]. J.M. Hilkert, “Inertially Stabilized Platform Technology: Concepts and 
Principles”, IEEE Control Systems Magazine, vol 28, February 2008. 
[3]. F. REIS, M., CARVALHO, G., NEVES, A., “ Dynamic Model and Line 
of Sight Control of a 3-DOF Inertial Stabilization Platform via Feedback 
Linearization" , IEEE American Control Conference 2018, June 2018. 
[4]. Michael K. Masten , “Inertially stabilized platforms for optical imaging 
systems”, IEEE Control Systems Magazine , Volume: 28, Feb. 2008. 
[5]. H.Goldstein, “Classical Mechanics”, Addison-Wesley, 2002. 
[6]. J. M. Hilkert, Gavin Kanga, K. K. “Line-of-sight kinematics and cor-rections 
for fast-steering mirrors used in precision pointing and tracking systems". 
Proceedings of SPIE - The International Society for Optical Engineering, v. 
9076, 2014. 
[7]. Wu-Sung Yao, Po-Wen Hsueh, Hsien-Tang Yeh,”Dynamic analysis and 
stabilizing control of three-axis spherical gimbal”,Vol 234, Issue 5, 2020. 
ABSTRACT 
KINEMATIC ANALYSIS OF LINE OF SIGHT STABILIZATION SYSTEMS 
Line of sight stabilization systems has many uses in radars, satellite 
communications and tracking system on moving vehicles. The design for line 
of sight stabilization system should be based on system kinematics. In this 
paper, building geometric anh kinematics equations of line of sight 
stabilization 3-axis as basic of control system design and some simulation 
results is presented. 
Keywords: Line of sight stabilization; Kinematic of 2D gimbal; Dynamic of gimbal. 
Nhận bài ngày 20 tháng 02 năm 2020 
Hoàn thiện ngày 29 tháng 7 năm 2020 
Chấp nhận đăng ngày 28 tháng 8 năm 2020 
Địa chỉ: 1Viện Tự động hóa KTQS, Viện KHCN quân sự; 
2Cục Khoa học quân sự. 
*
Email: vuminhkhiem@yahoo.com.