Optimized rational phase mask to extend the depth of field in imaging systems
In recent years, wavefront coding is well known as a powerful technique which
can be employed to extend the depth of field of an imaging system. Wavefront
coding is a hybrid imaging technique and it includes two parts: the optics and the
digital processing step. By placing a phase mask in the exit pupil plane, the
modulation transfer function (MTF) or the point spread function (PSF) reduces
sensitivity to defocus error. Then, middle images which are captured by a detector
are the same blurred images to defocus error and become sharp and clear after
using a simple deconvolution filter to decode them in the digital processing step.
Conversely, in traditional imaging systems, the aim of the optics is to result in an
imaging as sharp and clear as possible. After that, the image might be
postprocessed to reveal information that are relevant to a specific application.
However, the optimizations of the optics and the postprocessing are implemented
separately. Moreover, in comparison between the wavefront coding system and
traditional imaging system under the impact of defocus, the MTF of an wavefront
coding system is lower than that of traditional imaging system. It introduces no
zeros in the MTF of an wavefront coding system. Therefore, all frequencies can be
restored to near diffraction-limited performance.
In wavefront coding system, there are two parts which are designed together.
However, the most important part of wavefront coding system lies in the design of
suitable phase masks to obtain the defocus invariant characteristics. As a result,
many researchers keep focusing on the development of this technique in term of
phase masks. So far, many kinds of odd asymmetrical phase masks to increase the
depth extension, such as cubic phase mask [1], logarithmic phase mask [2-5],
exponential phase mask [6], sinusoidal phase mask, [7, 8], polynomial phase mask
[9], free-form phase mask [10], rational phase mask [11], tangent phase mask [12],
and high-order phase mask [13], have been reported. All these phase masks can
achieve the goal of the depth of field extension.

Trang 1

Trang 2
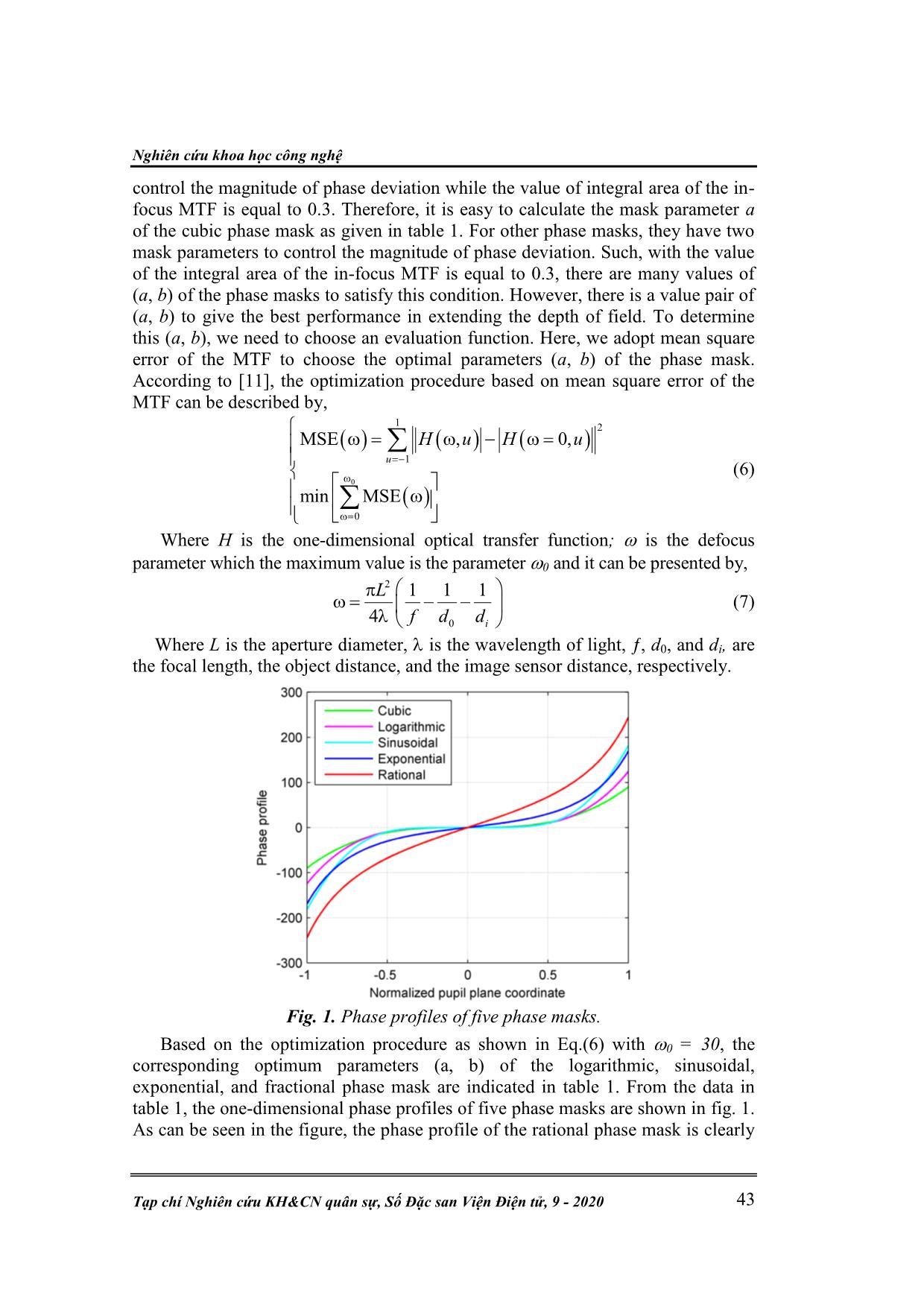
Trang 3

Trang 4
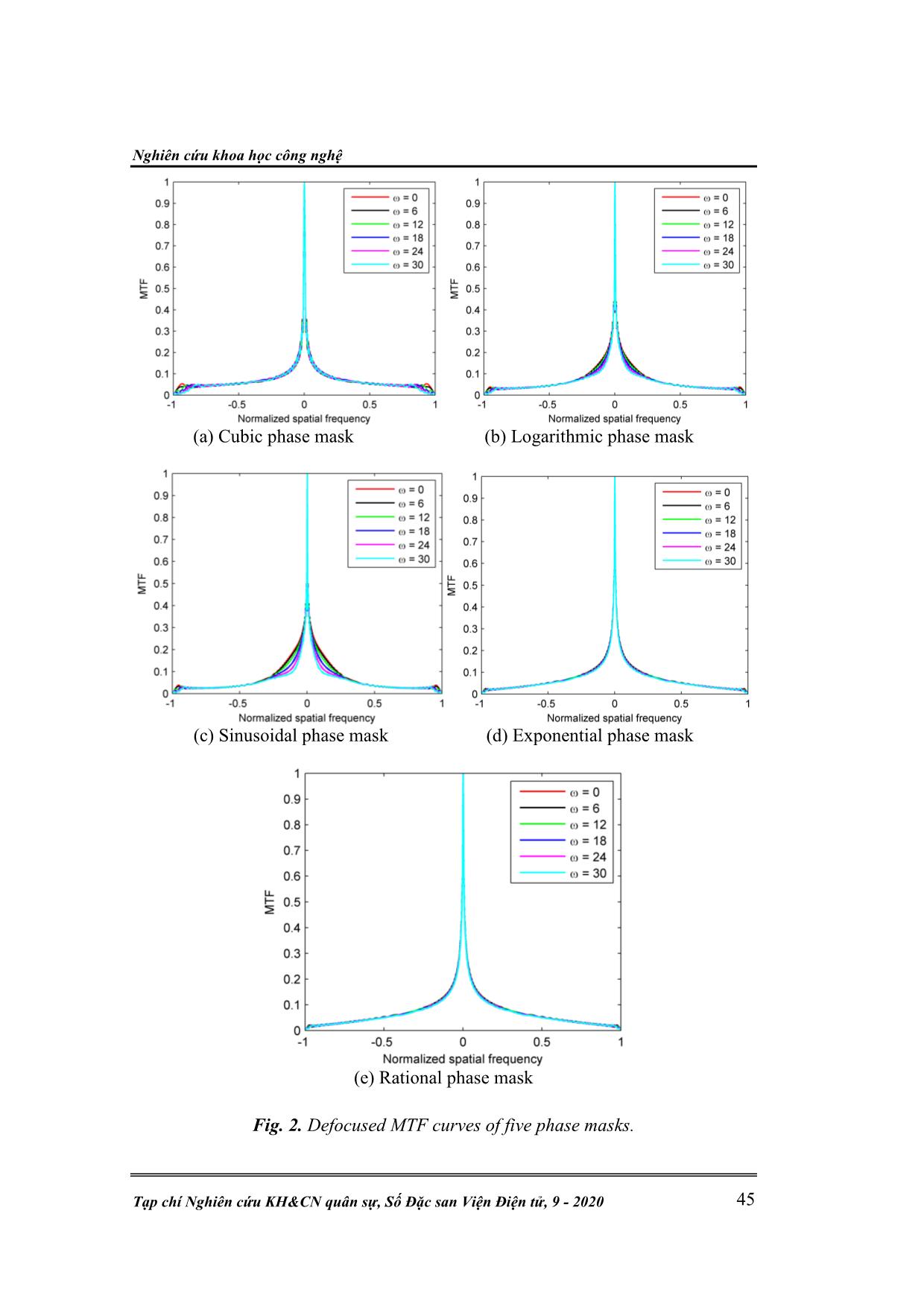
Trang 5
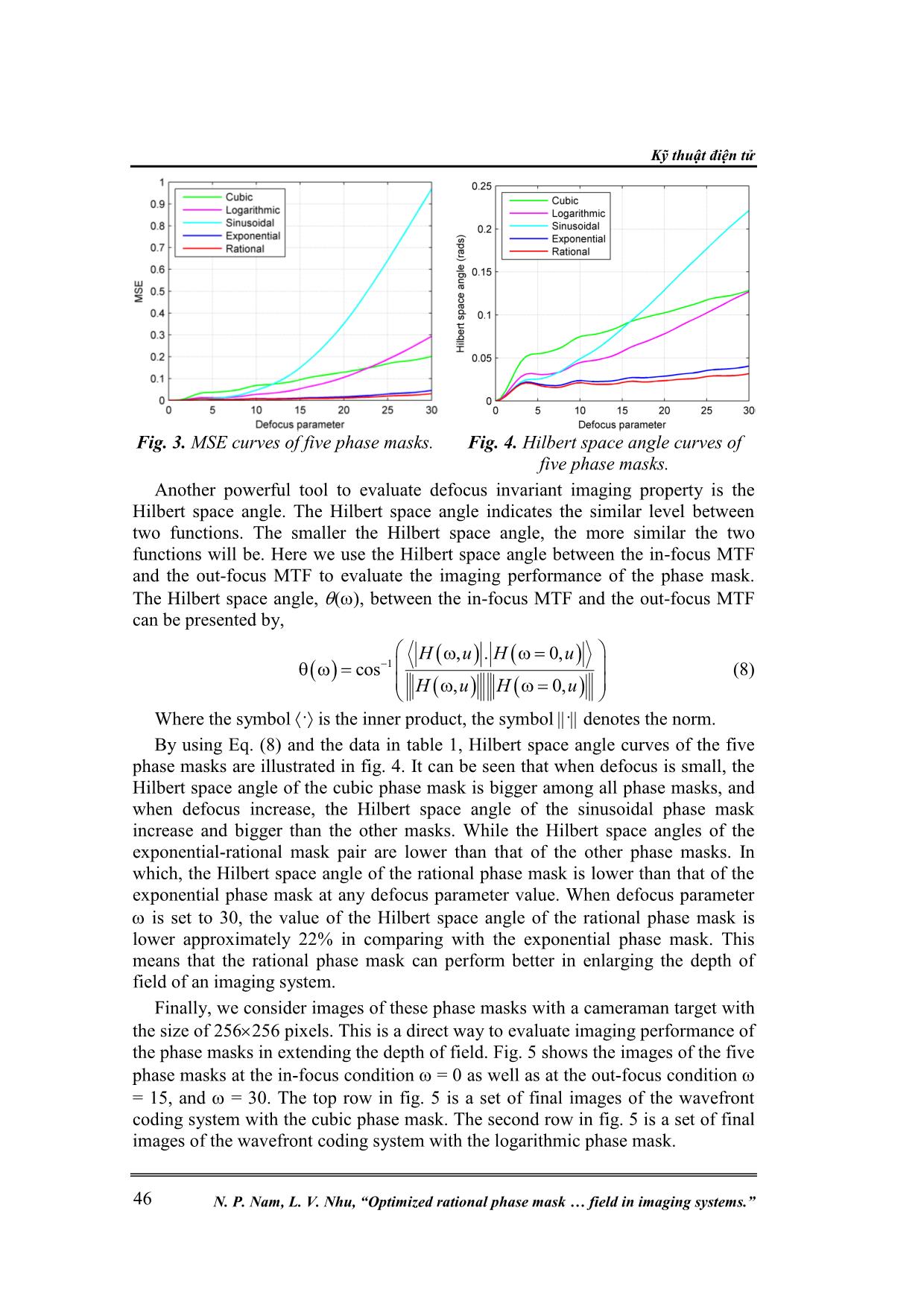
Trang 6

Trang 7

Trang 8

Trang 9
Tóm tắt nội dung tài liệu: Optimized rational phase mask to extend the depth of field in imaging systems

Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 41 OPTIMIZED RATIONAL PHASE MASK TO EXTEND THE DEPTH OF FIELD IN IMAGING SYSTEMS Nguyen Phuong Nam 1* , Le Van Nhu 2 Abstract: Wavefront coding technique includes the optics and the digital processing step to the final high-quality images. One of the most important parts of wavefront coding technique is the design of a suitable phase mask to obtain the defocus invariant characteristics. In this paper, we proposed a simple rational phase mask with two mask parameters to extend the depth of field. A series of performance comparison between the proposed phase mask with the cubic, logarithmic, sinusoidal, and exponential phase mask is presented. The simulation results demonstrated that the proposed phase mask is superior to other compared methods relating to imaging performance in extending the depth of field of an imaging system. Keywords: Wavefront coding; Phase mask; Depth of field. 1. INTRODUCTION In recent years, wavefront coding is well known as a powerful technique which can be employed to extend the depth of field of an imaging system. Wavefront coding is a hybrid imaging technique and it includes two parts: the optics and the digital processing step. By placing a phase mask in the exit pupil plane, the modulation transfer function (MTF) or the point spread function (PSF) reduces sensitivity to defocus error. Then, middle images which are captured by a detector are the same blurred images to defocus error and become sharp and clear after using a simple deconvolution filter to decode them in the digital processing step. Conversely, in traditional imaging systems, the aim of the optics is to result in an imaging as sharp and clear as possible. After that, the image might be postprocessed to reveal information that are relevant to a specific application. However, the optimizations of the optics and the postprocessing are implemented separately. Moreover, in comparison between the wavefront coding system and traditional imaging system under the impact of defocus, the MTF of an wavefront coding system is lower than that of traditional imaging system. It introduces no zeros in the MTF of an wavefront coding system. Therefore, all frequencies can be restored to near diffraction-limited performance. In wavefront coding system, there are two parts which are designed together. However, the most important part of wavefront coding system lies in the design of suitable phase masks to obtain the defocus invariant characteristics. As a result, many researchers keep focusing on the development of this technique in term of phase masks. So far, many kinds of odd asymmetrical phase masks to increase the depth extension, such as cubic phase mask [1], logarithmic phase mask [2-5], exponential phase mask [6], sinusoidal phase mask, [7, 8], polynomial phase mask [9], free-form phase mask [10], rational phase mask [11], tangent phase mask [12], and high-order phase mask [13], have been reported. All these phase masks can achieve the goal of the depth of field extension. Although many phase masks have been mentioned above, there are two main methods to research a phase mask. One is based on resolution analysis using the Kỹ thuật điện tử N. P. Nam, L. V. Nhu, “Optimized rational phase mask field in imaging systems.” 42 stationary phase approximation method, as in the cubic phase mask [1] by minimizing the variation of the optical transfer function to the defocus, or in the given logarithmic phase mask by making the point spread function insensitive to the defocus [2]. Other methods are based on the optimization of parameters of the phase mask. By using this method, many phase masks with high performance in extending the depth of field were presented, as in [3-13]. However, the second method should use an evaluation function. Some evaluation functions have been widely applied to optimize parameters of the phase mask, such as the Fisher information, the mean square error of the MTF or the PSF. With each evaluation function, two conditions should be considered. The first one, the magnitude of the MTF should big enough to make the digital processing easier. The second one, the optical transfer function (OTF) should be invariant enough to defocus. According to [1, 4, 6, 7], the cubic, the improved logarithmic, the exponential, and the sinusoidal phase mask can be given by Eqs.(1)-(4), respectively, as follows: 3 3,f x y ax ay (1) 4 4, sgn log sgn logf x y x ax x b y ay y b (2) 2 2, exp expf x y ax bx ay by (3) 4 4, sin sinf x y ax bx ay by (4) Where x and y are the pupil plane coordinates; both a and b denote the phase mask parameters to control the magnitude of phase deviation; sgn(·) describes the sign function which is defined as 1 for x 0 and -1 for x 0. The high performance of the rational phase mask is demonstrated in [11]. However, this rational phase mask has twenty-four mask parameters to control the magnitude of phase deviation. It is relatively complex. Hence, in this paper, the aim of work is to find a simple phase type of rational phase function to obtain the invariant modulation transfer function over a wide range of defocus. Based on using optimization method, and from trial and error, we propose a simple rational phase mask with two mask parameters to control the magnitude of the phase deviation. Nonetheless, this mask can obtain the high performance in extending the depth of field. The proposed rational phase mask can be presented by, 2 2, ax ay f x y b x b y (5) where these symbols in Eq. (5) have meaning the same as above, but b 1. 2. OPTIMIZATION OF PHASE MASK PARAMETERS To make performance comparison between five phase masks, these five masks should be determined under the same condition. Firstly, the integral areas of the in- focus MTF for the five phase masks are the same. This condition ensures that the phase masks have the same ability to transfer signal. In this paper, we choose the value of the integral area of the in-focus MTF for the five phase masks is equal 0.3. With this value, the digital processing can make certain to obtain the restored final high-quality images. For the cubic phase mask, it has only one mask parameter to Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 43 control the magnitude of phase deviation while the value of integral area of the in- focus MTF is equal to 0.3. Therefore, it is easy to calculate the mask parameter a of the cubic phase mask as given in table 1. For other phase masks, they have two mask parameters to control the magnitude of phase deviation. Such, with the value of the integral area of the in-focus MTF is equal to 0.3, there are many values of (a, b) of the phase masks to satisfy this condition. However, there is a value pair of (a, b) to give the best performance in extending the depth of field. To determine this (a, b), we need to choose an evaluation function. Here, we adopt mean square error of the MTF to choose the optimal parameters (a, b) of the phase mask. According to [11], the optimization procedure based on mean square error of the MTF can be described by, 0 1 2 1 0 MSE , 0, min MSE u H u H u (6) Where H is the one-dimensional optical transfer function; is the defocus parameter which the maximum value is the parameter 0 and it can be presented by, 2 0 1 1 1 4 i L f d d (7) Where L is the aperture diameter, is the wavelength of light, , d0, and di, are the focal length, the object distance, and the image sensor distance, respectively. Fig. 1. Phase profiles of five phase masks. Based on the optimization procedure as shown in Eq.(6) with 0 = 30, the corresponding optimum parameters (a, b) of the logarithmic, sinusoidal, exponential, and fractional phase mask are indicated in table 1. From the data in table 1, the one-dimensional phase profiles of five phase masks are shown in fig. 1. As can be seen in the figure, the phase profile of the rational phase mask is clearly Kỹ thuật điện tử N. P. Nam, L. V. Nhu, “Optimized rational phase mask field in imaging systems.” 44 separate to the other phase masks when the variation of height of the rational phase mask profile is faster than the other phase masks. Table 1. Optimum parameters of five phase masks. a b Cubic 89.85 Logarithmic 139.99 -3.43 Sinusoidal 189.94 1.87 Exponential 42.99 1.37 Rational 229.68 1.94 3. PERFORMANCE COMPARISON FOR PHASE MASKS With the data in table 1, we can illustrate defocused MTF curves of the five phase masks at the in-focus condition = 0 as well as at the out-focus condition, = 6, 12, 18, 24 and 30 as given in fig. 2. The defocused MTF curves of the cubic phase mask are indicated in fig. 2(a). The defocused MTF curves of the logarithmic phase mask are shown in fig. 2(b). The defocused MTF curves of the sinusoidal phase mask are given in fig. 2(c). Fig. 2(d) shows the defocused MTF curves of the exponential phase mask. The defocused MTF curves of the rational phase mask are presented in fig. 2(e). From fig. 2, it is clear that the defocused MTF curves of the five phase masks are less sensitive to defocus. However, the defocused MTF curves of the cubic, logarithmic, and sinusoidal phase mask are less invariant than that of the other phase masks because the defocused MTF curves of the cubic phase mask present a strong oscillations at high spatial frequency part, while the two logarithmic and sinusoidal phase masks have noticeable oscillations at low and high spatial frequency parts. The defocused MTF curves for the two exponential and rational phase masks have high stability. However, it can be seen that the defocused MTF curves of the rational phase mask is more invariant than that of the exponential phase mask. Therefore, the rational phase mask could perform better in extending the depth of field of an imaging system. Besides the defocused MTF, another approach to evaluate the defocus invariant characteristic of an imaging system with a phase mask is the mean square error of the MTF (MSE) as given in Eq. (6). The MSE reveals the stable level of the defocused MTF. The lower the MSE is, the higher invariant to defocus the phase mask. Fig. 2 shows that MSE curves of the five phase masks corresponding to their optimum parameters which are listed in table 1. From fig. 2, it is clear that the MSE of the sinusoidal phase mask is bigger among all phase masks, while the MSE of the exponential-rational mask pair is lower than that of the cubic- logarithmic mask pair. The MSE of the rational phase mask is lower than that of the exponential phase mask. The value of the MSE of the rational phase mask is lower approximately 32% in comparison with the exponential phase mask at the defocus parameter = 30. So the rational phase mask is less sensitive to defocus. Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 45 (a) Cubic phase mask (b) Logarithmic phase mask (c) Sinusoidal phase mask (d) Exponential phase mask (e) Rational phase mask Fig. 2. Defocused MTF curves of five phase masks. Kỹ thuật điện tử N. P. Nam, L. V. Nhu, “Optimized rational phase mask field in imaging systems.” 46 Fig. 3. MSE curves of five phase masks. Fig. 4. Hilbert space angle curves of five phase masks. Another powerful tool to evaluate defocus invariant imaging property is the Hilbert space angle. The Hilbert space angle indicates the similar level between two functions. The smaller the Hilbert space angle, the more similar the two functions will be. Here we use the Hilbert space angle between the in-focus MTF and the out-focus MTF to evaluate the imaging performance of the phase mask. The Hilbert space angle, (), between the in-focus MTF and the out-focus MTF can be presented by, 1 , . 0, cos , 0, H u H u H u H u (8) Where the symbol · is the inner product, the symbol · denotes the norm. By using Eq. (8) and the data in table 1, Hilbert space angle curves of the five phase masks are illustrated in fig. 4. It can be seen that when defocus is small, the Hilbert space angle of the cubic phase mask is bigger among all phase masks, and when defocus increase, the Hilbert space angle of the sinusoidal phase mask increase and bigger than the other masks. While the Hilbert space angles of the exponential-rational mask pair are lower than that of the other phase masks. In which, the Hilbert space angle of the rational phase mask is lower than that of the exponential phase mask at any defocus parameter value. When defocus parameter is set to 30, the value of the Hilbert space angle of the rational phase mask is lower approximately 22% in comparing with the exponential phase mask. This means that the rational phase mask can perform better in enlarging the depth of field of an imaging system. Finally, we consider images of these phase masks with a cameraman target with the size of 256 256 pixels. This is a direct way to evaluate imaging performance of the phase masks in extending the depth of field. Fig. 5 shows the images of the five phase masks at the in-focus condition = 0 as well as at the out-focus condition = 15, and = 30. The top row in fig. 5 is a set of final images of the wavefront coding system with the cubic phase mask. The second row in fig. 5 is a set of final images of the wavefront coding system with the logarithmic phase mask. Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 47 Fig. 5. Simulation images of cameraman target (rows: cubic, logarithmic, sinusoidal, exponential, and rational; columns: =0, = 15, and = 30). Kỹ thuật điện tử N. P. Nam, L. V. Nhu, “Optimized rational phase mask field in imaging systems.” 48 The third row in fig. 5 is a set of final images of the wavefront coding system with the sinusoidal phase mask. The fourth row in fig. 5 is a set of final images of the wavefront coding system with the exponential phase mask. The bottom row in fig. 5 is a set of final images of the wavefornt coding system with a rational phase mask. As can be seen in fig. 5, the image with the cubic phase mask is more degraded during the digital processing, such as artifacts on images, especially when defocus parameter is bigger. The image degradation of the cubic phase mask comes from the oscillations and the spatial frequency cutoff of its defocused MTF as shown in fig. 2 (a). The quality of restored final images from the logarithmic- sinusoidal mask pair is almost the same and is better than that of the cubic phase mask. Whereas the exponential-rational mask pair provide a better image quality among all phase masks. Additionally, the visual perception of the rational phase mask is likely better than that of the exponential phase mask. Hence, the rational phase mask could be better in extending the depth of field of an imaging system. 4. CONCLUSION In the paper, the simple rational phase mask to reduce the impact of defocus error in the modulation transfer function has proposed. Based on the evaluation of different methods such as: evaluation ways of the defocused MTF, the mean square error of the MTF, and Hilbert space angle between the in-focus MTF, the out-focus MTF and image restoration, it can be concluded that the proposed phase mask has remarkable improvement in imaging performance in extending the depth of field of an imaging system. Practically, it is feasible that a series of rational phase masks can be employed to enlarge the depth of field. Additionally, noise effect to image quality will be also investigated. This issue will be further studied in the future. REFERENCES [1]. E. R. Dowski, Jr. and W. T. Cathey, “Extended depth of field through wave- front coding,” Appl. Opt. 34, 1859-1866 (1995). [2]. S. S. Sherif, E. R. Dowski, and W. T. Cathey, “A logarithmic phase filter to extend the depth of field of incoherent hybrid imaging systems,” Proc. SPIE. 4471, 272 -279 (2001). [3]. H. Zhao and Y. Li, “Performance of an improved logarithmic phase mask with optimized parameters in a wavefront-coding system,” Appl. Opt. 49, 229-238 (2010). [4]. H. Zhao and Y. Li, “Optimized logarithmic phase masks used to generate defocus invariant modulation transfer function for wavefront coding system,” Opt. Lett. 35, 2630 -2632 (2010). [5]. H. Zhao, Q. Li and H. Feng, “Improved logarithmic phase mask to extend the depth of field of an incoherent imaging system,” Opt. Lett. 33, 1171-1173 (2008). [6]. Q. Yang, L. Liu, and J. Sun, “Optimized phase pupil masks for extended depth of field,” Opt. Commun. 272, 56-66 (2007). [7]. H. Zhao and Y. Li, “Optimized sinusoidal phase mask to extend the depth of field of an incoherent imaging system,” Opt. Lett. 35, 267-669 (2010). Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 49 [8]. J. Wang, J. Bu, M. Wang, Y. Yang and X. C. Yuan, “Improved sinusoidal phase plate to extend depth of field in incoherent hybrid imaging systems,” Opt. Lett. 37, 4534-4535 (2012). [9]. N. Caron and Y. Sheng, “Polynomial phase mask for extending depth-of-field optimized by simulated annealing,” Proc. SPIE 6832, 68321G-1-10 (2007). [10]. Y. Takahashi, and S. Komatsu, “Optimized free-form phase mask for extension of depth of field in wavefront-coded imaging,” Opt. Lett. 33, 1515- 1517 (2008). [11]. F. Zhou, G. Li, H. Zhang, and D. Wang, “Rational phase mask to extend the depth of field in optical-digital hybrid imaging systems,” Opt. Lett. 34, 380- 382 (2009). [12]. V. N. Le, Z. Fan, S. Chen, “Optimized asymmetrical tangent phase mask to obtain defocus invariant modulation transfer function in incoherent imaging system,” Opt. Lett. 39, 2171-2174 (2014). [13]. A. Sauceda and J. O eda-Casta n eda, “High focal depth with fractional- power wave fronts,” Opt. Lett. 29, 560-562 (2004). TÓM TẮT MẶT NẠ PHA HÀM PHÂN THỨC TỐI ƯU MỞ RỘNG ĐỘ SÂU TRƯỜNG TRONG HỆ THỐNG TẠO ẢNH Công nghệ mã hóa mặt sóng bao gồm các bước tạo ảnh quang học và quá trình xử lý số cho nhận ảnh chất lượng cao. Phần quan trọng nhất của công nghệ mã hóa mặt sóng nằm ở thiết kế mặt nạ pha phù hợp để nhận các đặt tính bất biến lệch tiêu. Ở bài báo này, chúng tôi đề xuất một mặt nạ pha hàm phân thức với hai tham số cho mở rộng độ sâu trường. Một loạt các so sánh được tính toán giữa mặt nạ pha đề xuất với các mặt nạ pha hàm bậc ba, hàm logarit, hàm sin, hàm mũ được trình bày. Các kết quả mô phỏng đã chứng minh rằng, mặt nạ pha đề xuất có khả năng cao cho mở rộng độ sâu trường của một hệ thống tạo ảnh. Keywords: Wavefront coding; Phase mask; Depth of field. Nhận bài ngày 26 tháng 3 năm 2020 Hoàn thiện ngày 28 tháng 7 năm 2020 Chấp nhận đăng ngày 28 tháng 8 năm 2020 Địa chỉ: 1Institute of Electronics, Academy of Military Science and Technology; 2 Le Quy Don Technical University. * Email: ngnamaus41@gmail.com.
File đính kèm:
 optimized_rational_phase_mask_to_extend_the_depth_of_field_i.pdf
optimized_rational_phase_mask_to_extend_the_depth_of_field_i.pdf

