Nghiên cứu xây dựng công thức bán thực nghiệm tính toán hệ số truyền sóng qua đê ngầm cọc có cấu tạo phức hợp

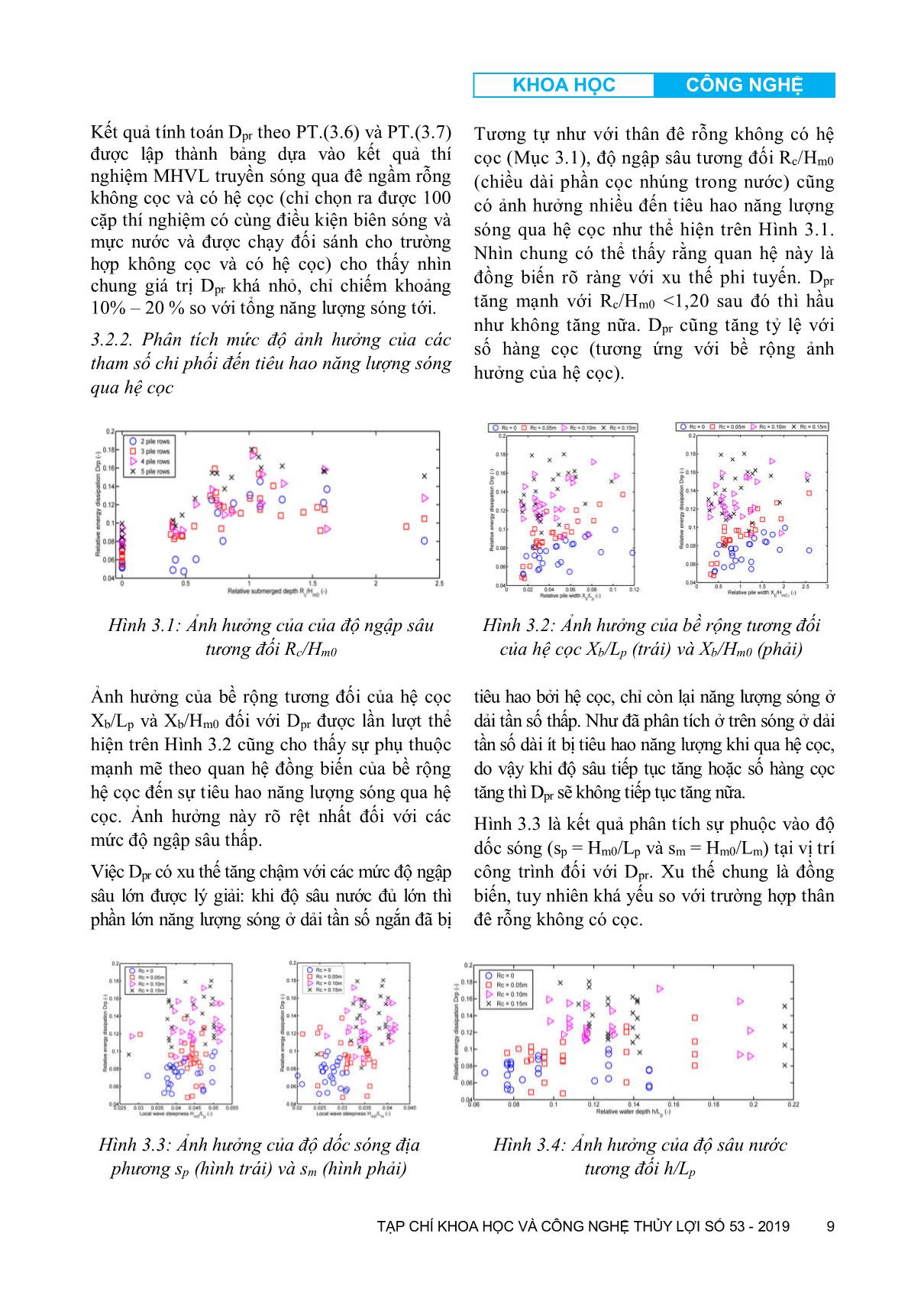
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 1
NGHIÊN CỨU XÂY DỰNG CÔNG THỨC BÁN THỰC NGHIỆM 
 TÍNH TOÁN HỆ SỐ TRUYỀN SÓNG QUA ĐÊ NGẦM CỌC CÓ 
CẤU TẠO PHỨC HỢP 
Nguyễn Anh Tiến 
Viện Kỹ thuật biển 
Thiều Quang Tuấn 
Trường Đại học Thủy lợi 
Tóm tắt: Bài báo trình bày phương pháp nghiêu cứu xây dựng công thức bán thực nghiệm tính 
toán hệ số truyền sóng qua đê ngầm cọc có cấu tạo phức hợp trên cơ sở lý thuyết là các phương 
trình cân bằng năng lượng của sóng ngẫu nhiên truyền vuông góc qua đê kết hợp với các nghiên 
cứu thực nghiệm trên mô hình vật lý thu nhỏ trong máng sóng thủy lực cho 2 dạng đê ngầm rỗng 
(không cọc) và đê ngầm rỗng có hệ cọc bên trên. Công thức bán thực nghiệm thể hiện rõ quá 
trình tương tác và cơ chế tiêu hao năng lượng sóng giữa hai bộ phận là thân đê rỗng và hệ cọc 
bên trên với sóng là độc lập với nhau, trong đó thành phần năng lượng sóng tiêu hao do thân đê 
rỗng (không có cọc) chịu sự chi phối chủ yếu của ba tham số chính là [độ sâu ngập nước tương 
đối của đỉnh đê (Rc/Hm0), bề rộng tương đối của đỉnh đê (B/Hm0), độ dốc sóng tại vị trí công 
trình (sm =Hm0/Lm)] và thành phần năng lượng sóng tiêu hao do hệ cọc bên trên chịu sự chi phối 
chủ yếu của hai tham số chính là [độ ngập sâu tương đối hay chiều dài phần cọc nhúng trong 
nước (Rc/Hm0) và bề rộng tương đối của hệ cọc (Xb/Lm)]. 
Từ khóa: công thức bán thực nghiệm, đê ngầm cọc phức hợp, đê ngầm dạng rỗng, hệ cọc giảm 
sóng, hệ số truyền sóng, mô hình vật lý, năng lượng sóng, tham số chi phối. 
Summary: This article proposes semi-empirical equations to estimate wave transmission 
coefficient through submerged complex with solid piles breakwater base on theories of energy 
conservation of perpendicular wave transmission incorporate with physical hydraulic 
experiments in wave flume apply on both types of submerged breakwater with and without piles. 
These equations are able to describe interactions and energy dissipation process for each 
element of this complex structure which are foundation block and pile rows. Energy dissipation 
process depends on three major factors which are [relative submerge depth (Rc/Hm0), relative 
crest width (B/Hm0), wave slope at construction location (sm =Hm0/Lm)] and wave energy 
dissipation process through piles rows is determined by two major factors [relative submerge 
depth or submerge length of piles (Rc/Hm0) and relative pile rows width (Xb/Lm)]. 
Keywords: semi-empirical equation, submerged complex with solid piles breakwater, permeable 
breakwater, piles wave dissipation, wave transmission coefficient, physical model, wave energy, 
definition factor. 
1. ĐẶT VẤN ĐỀ * 
Đê giảm sóng ngầm (ĐGS) là dạng công trình 
chủ động được nhiều nước phát triển trên thế 
giới như Mỹ, Nhật Bản, Pháp, Anh, Ý, tập 
Ngày nhận bài: 25/02/2019 
Ngày thông qua phản biện: 22/3/2019 
Ngày duyệt đăng: 26/3/2019 
trung nghiên cứu và ứng dụng để bảo vệ bờ 
biển do hiệu quả mang lại vượt trội so với các 
dạng công trình khác như mỏ hàn biển, kè 
biển,. Giải pháp này hiện nay được xem là 
đáp ứng được tiêu chí đa mục tiêu như giảm 
sóng chống sạt lở bảo vệ bờ biển, gây bồi tạo 
bãi, phục hồi hay hỗ trợ trồng lại rừng ngập 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 2
mặn bị xói lở, đồng thời giúp giảm thiểu tối đa 
các tác động tiêu cực đến môi trường tự nhiên 
sau khi xây dựng công trình [4][5]. 
Các nghiên cứu về ĐGS thường tập trung theo 
3 hướng chính là (i) nghiên cứu về kết cấu, (ii) 
nghiên cứu hiệu quả giảm sóng và (iii) nghiên 
cứu về hiệu quả gây bồi. Trong đó, nghiên cứu 
về hiệu quả giảm sóng của đê ngầm dạng đá 
đổ mái nghiêng là loại kết cấu mang tính 
truyền thống được quan tâm nghiên cứu nhiều 
nhất và cũng được sử dụng phổ biến nhất trên 
thế giới. Sau đó các nghiên cứu được mở rộng 
cho ĐGS dạng đá đổ phủ các khối dị hình như 
Tribar, Tetrapod, Dolos,. Các nghiên cứu 
gần đây có xu thế hướng đến sử dụng các dạng 
kết cấu mới phi truyền thống như đê trụ rỗng 
có lỗ tiêu sóng (hình bán nguyệt), cấu kiện L-
Block, cấu kiện AccropodeTM, cấu kiện 
AccropodeTM II, cấu kiện Core-LocTM, cấu 
kiện EcopodeTM,; dạng thân thiện với môi 
trường tự nhiên như dải ngầm nhân tạo 
(Artificial Reefball), kết cấu gờ ngầm P.E.P, 
kết cấu gờ ngầm WaveBlockTM, kết cấu gờ 
ngầm BeachSaverTM, kết cấu gờ ngầm Surger 
BreakerTM, kết cấu gờ ngầm BeachPrismTM, 
ống Geotube, túi địa kỹ thuật, hệ cọc giảm 
sóng (tiết diện tròn, vuông, chữ nhật, tam 
giác); hay dạng phi công trình như trồng cây 
ngập mặn [11]. 
Nghiên cứu chủ yếu được thực hiện thông qua 
các thí nghiệm mô hình vật lý thu nhỏ trong 
máng sóng thủy lực để xác lập mối quan hệ 
giữa các đặc trưng về thủy hải văn như (chiều 
cao sóng Hs, chu kỳ sóng Tp, độ sâu nước 
trước đê h, độ ngập đỉnh đê Rc) với các thông 
số đặc trưng hình học của đê như (bề rộng 
đỉnh đê B, chiều cao đê D, hệ số mái m) và cấu 
trúc vật liệu làm thân đê  ...  năng lượng sóng 
qua hệ cọc 
Tương tự như với thân đê rỗng không có hệ 
cọc (Mục 3.1), độ ngập sâu tương đối Rc/Hm0 
(chiều dài phần cọc nhúng trong nước) cũng 
có ảnh hưởng nhiều đến tiêu hao năng lượng 
sóng qua hệ cọc như thể hiện trên Hình 3.1. 
Nhìn chung có thể thấy rằng quan hệ này là 
đồng biến rõ ràng với xu thế phi tuyến. Dpr 
tăng mạnh với Rc/Hm0 <1,20 sau đó thì hầu 
như không tăng nữa. Dpr cũng tăng tỷ lệ với 
số hàng cọc (tương ứng với bề rộng ảnh 
hưởng của hệ cọc). 
Hình 3.1: Ảnh hưởng của của độ ngập sâu 
tương đối Rc/Hm0 
Hình 3.2: Ảnh hưởng của bề rộng tương đối 
của hệ cọc Xb/Lp (trái) và Xb/Hm0 (phải) 
Ảnh hưởng của bề rộng tương đối của hệ cọc 
Xb/Lp và Xb/Hm0 đối với Dpr được lần lượt thể 
hiện trên Hình 3.2 cũng cho thấy sự phụ thuộc 
mạnh mẽ theo quan hệ đồng biến của bề rộng 
hệ cọc đến sự tiêu hao năng lượng sóng qua hệ 
cọc. Ảnh hưởng này rõ rệt nhất đối với các 
mức độ ngập sâu thấp. 
Việc Dpr có xu thế tăng chậm với các mức độ ngập 
sâu lớn được lý giải: khi độ sâu nước đủ lớn thì 
phần lớn năng lượng sóng ở dải tần số ngắn đã bị 
tiêu hao bởi hệ cọc, chỉ còn lại năng lượng sóng ở 
dải tần số thấp. Như đã phân tích ở trên sóng ở dải 
tần số dài ít bị tiêu hao năng lượng khi qua hệ cọc, 
do vậy khi độ sâu tiếp tục tăng hoặc số hàng cọc 
tăng thì Dpr sẽ không tiếp tục tăng nữa. 
Hình 3.3 là kết quả phân tích sự phuộc vào độ 
dốc sóng (sp = Hm0/Lp và sm = Hm0/Lm) tại vị trí 
công trình đối với Dpr. Xu thế chung là đồng 
biến, tuy nhiên khá yếu so với trường hợp thân 
đê rỗng không có cọc. 
Hình 3.3: Ảnh hưởng của độ dốc sóng địa 
phương sp (hình trái) và sm (hình phải) 
Hình 3.4: Ảnh hưởng của độ sâu nước 
tương đối h/Lp 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 10
Các ảnh hưởng khác như độ sâu nước tương 
đối h/Lp và chỉ số vỡ Hm0/h đến Dpr được lần 
lượt trình bày trên các Hình 3.4 và 3.5 cho 
thấy các tham số này hầu như không có chi 
phối trực tiếp đến tiêu hao năng lượng sóng 
qua hệ cọc. 
Hình 3.5: Ảnh hưởng của chỉ số vỡ Hm0 /h 
Ngoài ra tiêu hao năng lượng sóng qua hệ cọc 
còn phụ thuộc vào mật độ cọc hay độ rỗng của 
đê ngầm cọc phức hợp (phụ thuộc khoảng cách 
giữa các cọc), đường kính cọc. Tuy nhiên trong 
thí nghiệm tham số này được giữ cố định do vậy 
không được xem xét một cách trực tiếp ở đây mà 
gián tiếp nằm trong các thông số khác được phân 
tích ở trên. 
3.2.3. Tiêu hao năng lượng sóng qua hệ cọc 
Với những phân tích tương quan nêu trên ở 
đây chúng ta sẽ xây dựng công thức thực 
nghiệm tính toán xác định năng lượng sóng bị 
tiêu hao bởi hệ cọc nằm phía trên thân đê rỗng. 
Một cách tương tự [9], chúng ta có phương 
trình tổng quát: 
D =  
R
H
,
X
L
 
(3.9) 
Dpr mang ý nghĩa là năng lượng sóng tiêu hao 
tương đối bởi hệ cọc so với tổng năng lượng 
sóng tới (Dpr còn có thể được hiểu là hiệu năng 
của hệ cọc Dpr <1). Như vậy Dpr phụ thuộc vào 
tổng thể tích phạm vi cản nước tương đối của 
hệ cọc so với toàn bộ thể tích khối nước dao 
động xét trong trong một chu kỳ sóng. Ngoài 
ra lưu ý khi Rc = 0 (mực nước ngang bằng thân 
đê rỗng) thì Dpr > 0 do một phần sóng vẫn 
truyền qua đỉnh đê và vẫn bị tiêu hao năng 
lượng bởi hệ cọc. 
Xuất phát từ những phân tích trên chúng ta có 
đề xuất tham số biểu diễn thể tích cản sóng 
tương đối của hệ cọc như sau: 
V =
V
V
=
(R + H). X
H. L
=
R + H
H
.
X
L
(3.10) 
trong đó: V là thể tích cản sóng tương đối của 
hệ cọc; Vp và Vw là thể tích phạm vi cản sóng 
của hệ cọc và tổng thể tích phần khối nước dao 
động xét trong một chu kỳ sóng. 
PT.(3.10) vẫn bảo toàn các tham số chi phối 
của của PT.(3.9). Hình 3.6 biểu diễn quan hệ 
giữa thể tích cản sóng tương đối của hệ cọc và 
Dpr, qua đó có thể thấy rằng tương tự như các 
phân tích tương quan ở phần trước Dpr có xu 
thế tăng khi V tăng, tức là khi độ ngập tương 
đối tăng hoặc bề rộng hệ cọc tăng. Khi V 
tăng đến một giới hạn nào đó thì Dpr không 
tăng nữa (lý do đã giải thích ở trên). Như vậy 
tương quan này tồn tại một số điều kiện biên 
như sau: có tiệm cận trên là Dpr, max và Dpr = 0 
khi không có hệ cọc (Xb = 0), và Dpr > 0 khi Rc 
= 0. Với những tính chất này và với đại lượng 
miêu tả hiệu năng (Dpr <1) thì hàm tanh(x) 
(với x <1) là một dạng hàm phù hợp. 
Sử dụng phương pháp hồi quy với bộ số liệu 
thí nghiệm chúng ta xây dựng được quan hệ 
đường hồi quy như sau (xem Hình 3.6), mức 
độ phù hợp cao R2 = 0,80. 
D
= 0,153 tanh 20,6
(R + H)
H
X
L
 
(3.11) 
Khi sử dụng Tp thay vì Tm-1,0 (Lp thay vì Lm) 
trong tính toán thì mức độ phù hợp với các số 
liệu thực nghiệm đạt được sẽ thấp hơn một 
chút (R2 = 0,71, xem Hình 3.7). Lúc này công 
thức xác định Dpr sẽ là: 
D
= 0,152 tanh 16,3
(R + H)
H
X
L
 
(3.12) 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 11
Hình 3.6: Đường hồi quy thực nghiệm xác 
định Dpr ~  (với Lm) (đê có hệ cọc) 
Hình 3.7: Đường hồi quy thực nghiệm xác định Dpr 
~  (với Lp) (đê có hệ cọc) 
3.3. Truyền sóng qua đê ngầm rỗng có hệ cọc 
Xuất phát từ PT.(2.1) và PT.(2.3) chúng ta 
thiết lập các phương trình cân bằng năng 
lượng sóng cho trường hợp đê ngầm rỗng 
không cọc và có hệ cọc bên trên như sau: 
- Khi đê ngầm rỗng không cọc: 
E = E
()
+ E
()
+ E
()
+ E
()
 (3.13) 
- Khi đê ngầm rỗng có hệ cọc bên trên: 
E = E
()
+ E
()
+ E
()
+ E
()
+ E
()
(3.14) 
trong đó: Et, Ed, Ep, Ef, và Er lần lượt là năng 
lượng của sóng phía sau đê, phần năng lượng 
tiêu hao bởi phần thân đê rỗng, bởi hệ cọc, ma 
sát và năng lượng sóng phản xạ lại. Etot là tổng 
năng lượng sóng (bao gồm cả sóng tới và sóng 
phản xạ trở lại từ công trình) Các chỉ số (0) và 
(p) tương ứng dùng để chỉ trường hợp đê 
không cọc và có hệ cọc. 
Giả thiết với cùng một tổng năng lượng sóng 
Etot, thì các thành phần năng lượng sóng bị tiêu 
hao bởi ma sát E
()
= E
()
 và thân đê E
()
=
E
()
 là như nhau trong cả hai trường hợp đê 
ngầm rỗng không cọc và có hệ cọc. Từ hai 
PT.(3.13) và PT.(3.14) ta có: 
E
()
− E
()
 + E
()
− E
()
 − E
()
= 0 
⇔
1
8
ρg(H,
()
− H,
()
) +
1
8
 ρgH,
 (C
()
− C
()
) −
DX
c
 = 0 
(3.15) 
với Cr (0 và p) là các hệ số phản xạ trong hai 
trường hợp đê không có cọc và có hệ cọc. 
PT.(3.15) có thể viết lại dưới dạng các hệ số 
truyền sóng (Kt= Hrms,t/Hrms,i) ở hai trường hợp 
bằng cách chia hai vế phương trình này cho năng 
lượng sóng tới đơn vị E = 1/8ρgH,
 ta có: 
⇔ (K
()
− K
()
) + (C
()
− C
()
) −
DX
1
8 ρgH,
 c
= 0 (3.16) 
Liên hệ PT.(3.16) với PT.(3.8) chúng ta có: 
⇔ (K
()
− K
()
) + (C
()
− C
()
) − D = 0 (3.17) 
Lưu ý: Chênh lệch năng lượng sóng phản xạ 
tương đối E
()
− E
()
/E = (C
()
− C
()
) 
có giá trị rất nhỏ và tỷ lệ thuận so với năng 
lượng sóng tiêu hao bởi thân đê có hệ cọc ví 
KHOA HỌC CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 12
dụ như trình bày trên Hình 3.8 có kết quả từ 
thực nghiệm. Do vậy ảnh hưởng chênh lệch về 
sóng phản xạ có thể được xét đến một cách 
gián tiếp thông qua Dpr với một hệ số điều 
chỉnh mô hình. 
Hình 3.8: Liên hệ giữa chênh lệch năng 
lượng sóng phản xạ tương đối và tiêu 
hao năng lượng do hệ cọc Dpr (đê có cọc) 
Hình 3.9: Hiệu chỉnh hệ số mô hình m 
với các số liệu thí nghiệm 
Từ PT.(3.17) chúng ta có thể đưa ra công thức 
bán thực nghiệm xác định hệ số truyền sóng 
qua đê rỗng có hệ cọc bên trên (hay kí hiệu 
khác là Kt) như sau: 
K = K
()
− . D 
 (3.18) 
trong đó: m là hệ số mô hình (theo lý thuyết 
thì m <1,0) được hiệu chỉnh với các số liệu thí 
nghiệm nhằm kể đến ảnh hưởng của sóng phản 
xạ và các sai lệch do các giả thiết đã nêu khác 
trong quá trình xây dựng công thức. 
Lưu ý: K
()
 là hệ số truyền sóng qua đê ngầm 
rỗng không cọc được xác định từ PT.(3.1) và 
Dpr là năng lượng sóng tương đối tiêu hao bởi 
hệ cọc được xác định theo PT.(3.11) hoặc 
PT.(3.12). Khi đê ngầm rỗng không cọc (Dpr = 
0) thì PT.(3.18) sẽ trở về PT.(3.1). 
Sử dụng các PT.(3.1), PT.(3.11) và PT.(3.18) 
cùng với bộ số liệu thí nghiệm cho trường hợp đê 
có cọc để xác định hệ số mô hình m (160 thí 
nghiệm). Kết quả trên Hình 3.9 cho thấy m = 0,94 
cho kết quả phù hợp tốt nhất với bộ số liệu thí 
nghiệm (R2 = 0,87). Hình 3.10 trình bày so sánh 
giữa kết quả tính toán Kt theo PT. (3.18) với hệ số 
mô hình m = 0,94 và bộ số liệu thí nghiệm.
Hình 3.10: So sánh kết quả tính toán hệ số 
truyền sóng với số liệu thực nghiệm cho trường 
hợp đê có hệ cọc (hệ số mô hình m = 0,94). 
Hình 3.11: Tổng hợp so sánh kết quả tính toán 
hệ số truyền sóng với toàn bộ số liệu thực 
nghiệm (đê không cọc và đê có hệ cọc). 
KHOA HỌC CÔNG NGHỆ 
 TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 13
Thay thế hệ số mô hình m = 0,94 vào 
PT.(3.18) ta có PT.(3.19) tổng quát như sau: 
K = K
()
− 0,94. D 
 (3.19) 
Sự phù hợp rất tốt của công thức bán kinh 
nghiệm PT.(3.19) với bộ số liệu thí nghiệm 
khẳng định tính đúng đắn của phương pháp và 
các giả thiết đưa ra trong quá trình xây dựng 
công thức. 
Sau cùng Hình 3.11 là so sánh tổng hợp giữa 
kết quả tính toán với tất cả các trường hợp có 
và không có hệ cọc (tổng số 260 thí nghiệm). 
4. KẾT LUẬN 
1. Bài báo giới thiệu dạng đê ngầm cọc phức 
hợp có kết cấu mới phi truyền thống lắp ghép 
linh hoạt bằng các cấu kiện đúc sẵn định hình 
để giảm sóng chống xói lở bảo vệ bờ biển 
(xem Hình 2.1). 
2. Theo số liệu đo đạc thực nghiệm đã thực 
hiện những đánh giá và phân tích độc lập về 
mức độ ảnh hưởng của các tham số chi phối 
đến quá trình tiêu hao năng lượng sóng làm 
suy giảm chiều cao sóng để từ đó xây dựng 
phương pháp tính toán truyền sóng qua đê 
trong trường hợp tổng quát. 
2.1. Truyền sóng qua thân đê rỗng không cọc 
chịu sự chi phối chủ yếu của ba tham số chính 
đó là: ảnh hưởng của độ sâu ngập nước tương 
đối của đỉnh đê Rc/Hm0, ảnh hưởng của bề rộng 
tương đối của đỉnh đê B/Hm0 và ảnh hưởng của 
tương tác sóng với mái đê thông qua giá trị độ 
dốc sóng tại vị trí công trình sm. 
2.2. Truyền sóng qua hệ cọc bên trên chịu sự 
chi phối chủ yếu của hai tham số chính đó là: 
ảnh hưởng của độ ngập sâu tương đối Rc/Hm0 
(chiều dài phần cọc nhúng trong nước) và ảnh 
hưởng của bề rộng tương đối của hệ cọc Xb/Lm 
(Xb là chiều rộng ảnh hưởng của số hàng cọc 
trên đỉnh đê ngầm xét theo phương truyền 
sóng, xác định bằng khoảng cách tim của 2 
hàng cọc biên ngoài cùng trên đỉnh đê theo 
phương truyền sóng). 
3. Xây dựng được ba công thức thực nghiệm 
độc lập, trong đó công thức tính toán thành 
phần năng lượng sóng tiêu hao do thân đê rỗng 
(không cọc) theo PT.(3.1) và hai công thức 
thực nghiệm tính toán thành phần năng lượng 
sóng tiêu hao bởi hệ cọc bên trên theo 
PT.(3.11) hay PT.(3.12). 
4. Xây dựng được công thức bán thực nghiệm 
tính toán hệ số truyền sóng qua đê ngầm rỗng 
có hệ cọc bên trên theo PT.(3.19) phản ảnh 
đầy đủ mức độ ảnh hưởng của các tham số chi 
phối đến hệ số truyền sóng Kt . 
PT.(3.19) được xây dựng có tính tổng quát 
trên cơ sở các tham số độc lập K
()
 xác định 
theo PT.(3.1) và D xác định theo PT.(3.11) 
hoặc PT.(3.12). Trường hợp đặc biệt khi đê 
không có cọc thì PT.(3.19) trở về PT.(3.1) 
tính toán hệ số truyền sóng qua thân đê rỗng 
(không có cọc). 
5. Thông qua việc so sánh tổng hợp giữa kết 
quả tính toán hệ số truyền sóng Kt theo 
PT.(3.19) và K
()
 theo PT.(3.1) với tổng số 
260 số liệu thực nghiệm trên mô hình vật lý 
trong máng sóng thủy lực về quá trình truyền 
sóng qua đê ngầm rỗng không cọc và có hệ 
cọc cho thấy sự phù hợp rất tốt giữa kết quả 
tính toán theo công thức với kết quả của bộ số 
liệu thí nghiệm. Điều này khẳng định tính 
đúng đắn của cơ sở lý thuyết, các lý luận và 
các giả thuyết khoa học đã được sử dụng trong 
quá trình nghiên cứu để xây dựng công thức 
trong trường hợp tổng quát. 
6. PT.(3.19) được lập có đầy đủ cơ sở khoa 
học, đảm bảo độ tin cậy và có khả năng ứng 
dụng vào thực tiễn để tính toán xác định hệ số 
truyền sóng cho dạng đê ngầm cọc phức hợp 
có kết cấu mới phi truyền thống. 
CHUYỂN GIAO CÔNG NGHỆ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ THỦY LỢI SỐ 53 - 2019 14
TÀI LIỆU THAM KHẢO 
[1] Cơ quan phát triển Pháp (AFD), Viện khoa học Thủy lợi Miền Nam (SIWRR) (2016-
2018). Nghiên cứu quá trình xói lở khu vực hạ lưu sông Mê Công và các biện pháp bảo vệ 
chống xói lở một cách bền vững cho vùng ven biển Gò Công và U Minh. Dự án vùng ven 
biển Đồng bằng sông Cửu Long (LMDCZ). 
[2] D’Angremond, K., Van der Meer, J.W., and de Jong, R.J., (1996). Wave transmission at 
low - crested breakwaters. Proceedings of the 25th Int. Conference of Coastal Engineering, 
Orlando, Florida, ASCE, 2418-2426. 
[3] Ferrant, V., (2007). Spectral analysis of wave transmission behind submerged 
breakwaters. PhD thesis, Italy. 
[4] Herbich, J., (1999). Offshore (Detached) Breakwaters. Hanbook of Coastal Engineering, 
Chapter 5. 
[5] Jonh R.Hsu, Takaaki Uda, Richard Silvester (1999). Shoreline Protection Methods - 
Japanese Exeperience. Hanbook of Coastal Engineering, Chapter 9. 
[6] Lê Đức Vĩnh, Nguyễn Anh Tiến, Lieou Kiến Chính (2018). Nghiên cứu chế độ sóng vùng 
biển từ mũi Cà Mau đến Kiên Giang. Tạp chí Khoa Học và Công Nghệ Thủy Lợi, Viện 
KHTL Việt Nam, Số 47 (9-2018), Trang 72-86. 
[7] Nguyễn Anh Tiến (2017). Hồ sơ sáng chế Đê ngầm giảm sóng liên kết gài răng lược lắp 
ghép chống xói lở bảo vệ bờ biển. Công báo sở hữu công nghiệp, Cục Sở hữu Trí tuệ, Tập 
A, Số 348, Trang 396. 
[8] Nguyễn Anh Tiến và nnk (2017). Nghiên cứu giải pháp hợp lý và công nghệ thích hợp 
phòng chống xói lở, ổn định bờ biển vùng đồng bằng sông Cửu Long, đoạn từ Mũi Cà Mau 
đến Hà Tiên. Đề tài độc lập cấp Nhà nước mã số ĐTĐL.CN-09/17, Viện Khoa học Thủy 
lợi Việt Nam, Hà Nội. 
[9] Nguyễn Anh Tiến, Trịnh công Dân, Lại Phước Quý, Thiều Quang Tuấn (2018). Nghiên 
cứu xây dựng phương pháp tính toán hệ số truyền sóng qua đê ngầm dạng rỗng bằng mô 
hình vật lý. Tạp chí Khoa Học và Công Nghệ Thủy Lợi, Viện KHTL Việt Nam, Số 46 (8-
2018), Trang 24-34. 
[10] Nguyễn Anh Tiến, Trịnh Công Dân, Thiều Quang Tuấn, Tô Văn Thanh (2018). Cơ sở 
khoa học xây dựng phương pháp tính toán hệ số truyền sóng qua đê ngầm cọc phức hợp. 
Tạp chí Khoa Học và Công Nghệ Thủy Lợi, Viện KHTL Việt Nam, Số 46 (8-2018), Trang 
81-87. 
[11] Nguyễn Viết Tiến (2015). Nghiên cứu hiệu quả của đê ngầm đến quá trình tiêu hao năng 
lượng sóng tác động vào bờ biển Việt Nam. Luận án Tiến sĩ kỹ thuật, Trường đại học Thủy 
lợi, Hà Nội. 
[12] Van der Meer, J.W., Briganti, R., Zanuttigh, B., Wang, B., (2005). Wave transmission and 
reflection at low-crested structures: design formulae, oblique wave attack and spectral 
change. Coastal Engineering, (52) 915-929.