Nghiên cứu, ứng dụng thuật toán thích nghi điều khiển chuyển động của robot trong không gian đề các
Đặt vấn đề
Sử dụng thuật toán điều khiển thích nghi
để điều khiển chuyển động robot trong không gian
khớp nhằm mục đích điều khiển góc quay của các
khớp (với các khớp quay) và chiều dài dịch chuyển
(đối với các khớp tịnh tiến) gọi chung là các biến
sao cho bám quỹ đạo đã đặt trước của các khớp khi
mà có các tác động từ sự thay đổi các tham số động
học của robot trong khi làm việc.
Trong thực tế và bằng thực nghiệm cho thấy,
điểm tác động cuối của cánh tay robot (đặt tại bàn
tay robot) được quy chiếu lên hệ trục tọa độ Oxyz
(hệ trục tọa độ đặt ở khớp đầu tiên của cánh tay
robot). Bài báo đưa ra ứng dụng thuật toán điều
khiển thích nghi để điều khiển chuyển động của
robot trong không gian Decac. Phương pháp điều
khiển này thay cho phương pháp điều khiển chuyển
động của robot trong không gian khớp để giảm sai
số tương đối khi quy chiếu hệ tọa độ đặt trên các
khớp lên hệ trục tọa độ gốc Oxyz

Trang 1

Trang 2
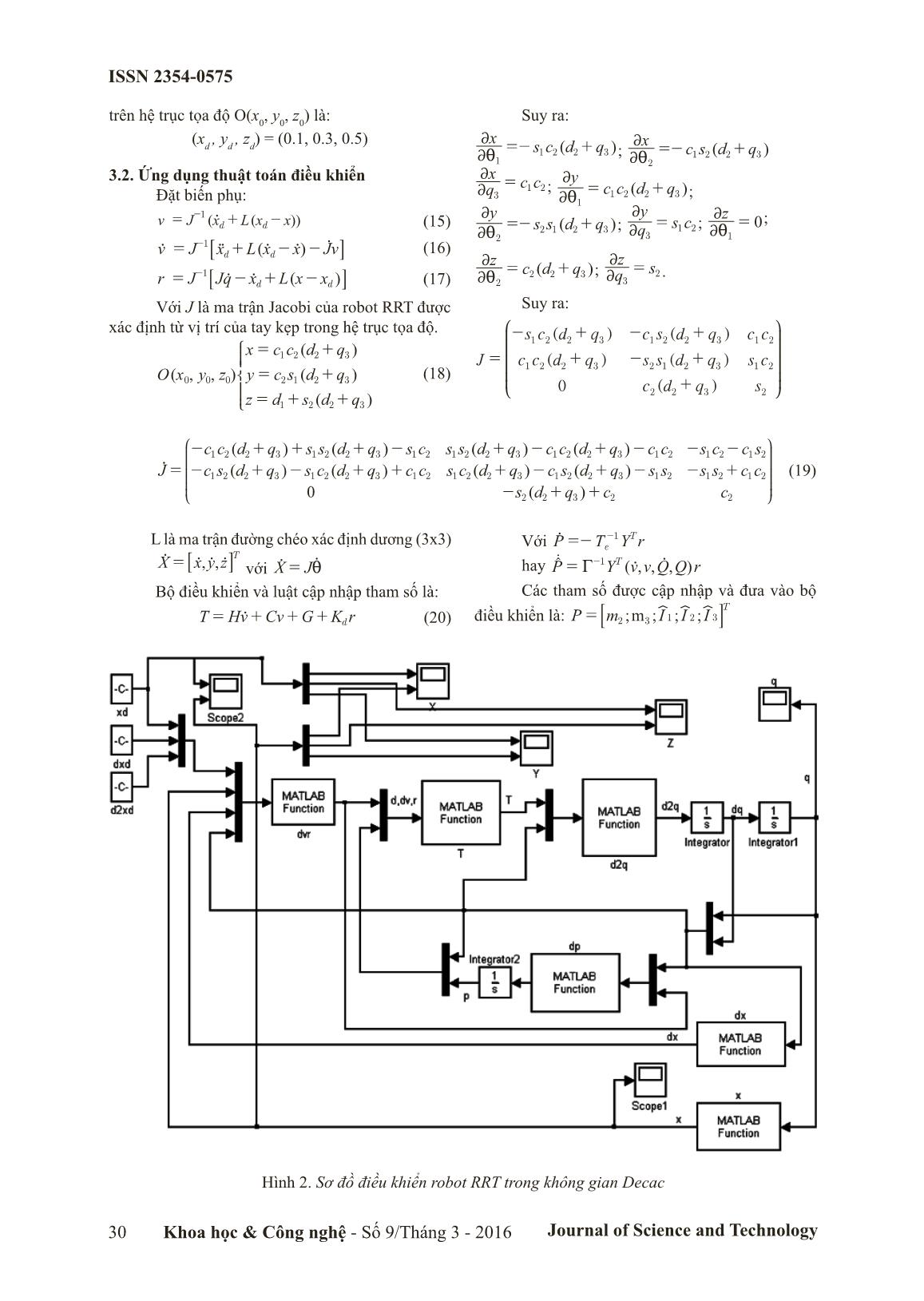
Trang 3

Trang 4

Trang 5
Tóm tắt nội dung tài liệu: Nghiên cứu, ứng dụng thuật toán thích nghi điều khiển chuyển động của robot trong không gian đề các

ISSN 2354-0575 Journal of Science and Technology28 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 NGHIÊN CỨU, ỨNG DỤNG THUẬT TOÁN THÍCH NGHI ĐIỀU KHIỂN CHUYỂN ĐỘNG CỦA ROBOT TRONG KHÔNG GIAN ĐỀ CÁC Đào Minh Tuấn, Nguyễn Thị Thúy, Nguyễn Thị Như Trường Đại học Sư phạm Kỹ thuật Hưng Yên Ngày nhận: 03/2/2016 Ngày xét duyệt: 09/3/2016 Tóm tắt: Để nâng cao chất lượng chuyển độngcủa robot công nghiệp, các bộ điều khiển sử dụng các thuật toán điều khiển như điều khiển trượt, PID bù trọng trường, tuyến tính hóa Tuy nhiên, trong một số điều kiện làm việc của robot công nghiệp, các tham số động học của robot thay đổi ví dụ như trọng lượng của vật mà cánh tay robot gắp, mô men quán tính của các khớp. Sự thay đổi này làm ảnh hưởng đến chất chuyển động, độ chính xác vị trí các khớp cũng như quỹ đạo chuyển động của robot. Bài báo này đề cập đến ứng dụng thuật toán điều khiển thích nghi điều khiển chuyển động của robot trực tiếp trong không gian Decac để hạn chế và loại bỏ sự ảnh hưởng đó. Từ khóa: Điều khiển robot, Điều khiển thích nghi, Điều khiển hệ thống có tham số không dừng. 1. Đặt vấn đề Sử dụng thuật toán điều khiển thích nghi để điều khiển chuyển động robot trong không gian khớp nhằm mục đích điều khiển góc quay của các khớp (với các khớp quay) và chiều dài dịch chuyển (đối với các khớp tịnh tiến) gọi chung là các biến sao cho bám quỹ đạo đã đặt trước của các khớp khi mà có các tác động từ sự thay đổi các tham số động học của robot trong khi làm việc. Trong thực tế và bằng thực nghiệm cho thấy, điểm tác động cuối của cánh tay robot (đặt tại bàn tay robot) được quy chiếu lên hệ trục tọa độ Oxyz (hệ trục tọa độ đặt ở khớp đầu tiên của cánh tay robot). Bài báo đưa ra ứng dụng thuật toán điều khiển thích nghi để điều khiển chuyển động của robot trong không gian Decac. Phương pháp điều khiển này thay cho phương pháp điều khiển chuyển động của robot trong không gian khớp để giảm sai số tương đối khi quy chiếu hệ tọa độ đặt trên các khớp lên hệ trục tọa độ gốc Oxyz. 2. Cơ sở lý thuyết 2.1. Xây dựng phương trình động lực học của robot 2.1.1. Môhình robot RRT Chuyển động của robot gồm 3 khớp. - Khớp 1: Chuyển động quay quanh trục Z 0 - Khớp 2: Chuyển động quay quanh trục Z 1 - Khớp 3: Chuyển động tịnh tiến theo trục Z2 Hình 1. Robot RRT Trong đó ,1 2i i là góc quay của khớp 1 và khớp 2; d 3 là chiều dài tịnh tiến của khớp 3. 2.1.2. Phương trình động lực robot Phương trình động lực học của cánh tay robot được xây dựng dưới dạng: ( ) ( , ) ( )M H Q Q V Q Q G Q= + +p o (1) Trong đó H, V, G lần lượt là các thành phần quán tính, tương hỗ và thành phần bù trọng trường thu được từ động học của robot. H I 4 m q s 1 4 q m s 1 d m s 1 d m q s 1 0 0 0 I I 4 m q 4 d m 4 d m d m q 0 0 0 4 m 1 3 3 2 2 2 2 2 2 2 2 2 2 3 2 2 2 3 3 2 2 1 2 2 3 2 2 2 2 2 2 3 2 3 3 3 = - - - - - - - + + + + + J L KKKKKKKKKKKK ^ ^ ^ ^ N P OOOOOOOOOOOO h h h h (2) ISSN 2354-0575 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 Journal of Science and Technology 29 V 4 m s c q q q 4 m q s 1 q q 2 d m s c q q 2d m c s q q d m s 1 q q 2d m s c q q q V m q q q 2 d m s c q q 2d m s c q q d m q q 2 m s c q q q 2d m s c q q q V d m q q 2 m q q q d m s 1 q q 2 m q s 1 q q 11 3 2 2 3 2 1 2 3 3 2 2 1 3 2 2 2 2 2 1 2 2 2 3 2 2 1 2 2 3 2 2 1 3 2 2 2 2 3 1 2 21 3 3 2 3 2 2 2 2 2 1 1 2 2 3 2 2 1 1 2 3 2 3 3 2 2 3 2 1 1 2 3 2 2 3 1 1 31 2 3 2 2 3 2 3 2 2 3 2 2 1 1 3 3 2 2 1 1 =- - - - - - - - = + + + + + = - + - + - o o o o o o o o o o o o o o o o o o o o o o o o ^ ^ ^ ^ h h h h (3) G 0 2 m c gq 2 d m c g d m c g 2 m s g 3 2 3 2 2 2 2 3 2 3 2 = + + R T SSSSSSSSSSSS V X WWWWWWWWWWWW (4) 2.2. Xây dựng thuật toán điều khiển thích nghi 2.2.1. Xây dựng thuật toán Xuất phát từ phương trình động lực học của robot (1) đã được xây dựng. Khi đặt một momen M vào các khác thì các khớp sẽ quay một góc là Q với T = [T 1 ; T2; .. Tn] ; Q = [q1; q2; .. qn] T là thành phần momen lấy từ bộ điều khiển, n là số bậc tự do của robot. Khi đó, gia tốc góc quay là: *Q H T V G1= - --p 6 @ (5) Khi cánh tay robot làm việc thì góc quay của các khớp, vận tốc các khớp và quán tính của các khớp thay đổi. Giả sử các tham số động học của hệ thống không biết lần lượt là thành phần khối lượng m i và thành phần quán tính là I i mà ta không biết. Ta phải ước lượng một giá trị của m i và I i . Momen hoặc lực cần thiết đưa vào các khớp được xác định là: ( ) ( , ) ( )M H Q v C Q Q v G Q K rD= + + +t o t o t (6) Trong đó: ( ) ( ) ( ) ( ) v q L q q v q L q q r q q L q q d d d d d d = - - = - - = - + - o o p o o o o Z [ \ ]]] ]]]] _ ` a bbb bbbb (7) q d là các giá trị góc đặt của các khớp. L là ma trận đường chéo xác định dương Dựa vào luật ước lượng từ phương trình động học ( ) ( ) ( , ) ( ) ( , , , ) M H Q Q H Q S Q Q Q G Q Y Q Q Q Q P 2 1 ( , )C Q Q = + + + = = p o o o p o o o > H1 2 344444444 44444444 (8) Với ma trận hồi quy ( , , , )Y Q Q Q Q Pp o o Trong đó: P = [m 1 ; ..m n ; I 1 ; ..I n ] Ta có luật cập nhập để tính Pto ( , , , )P Y v v Q Q rT1C= -to o o (9) Từ luật cập nhập đó, ta tính được các tham số ..... ..... m m I I n n 1 1 )X XU U Đặt ( ) ( ) ( , ) ( , ) H H Q H Q C C Q Q C Q Q G G G D D D = - = - = - t t o o t Z [ \ ]]] ]]]] (10) Thay vào phương trình (6) ta có ( ) ( ) ( ) ( ) H H v C C v G G K r HQ CQ G Q DD D D+ + + + + + = + += o p o (11) ( ) ( ) . .H v Q C v Q H v C v G K r ( , , , ) D Y V V Q Q P D D D- + - + + + =- D o p o o o o 1 2 3444444444 444444444 (12) Suy ra: ( , , , )Hr Cr Y V V Q Q P K rDD- + =-o o o (13) 2.2.2. Chứng minh thuật toán Chọn hàm Lyuapunov: ( )V r H Q r P P2 1 T TD CD= +6 @ (14) Trong đó, C là ma trận đường chéo xác định dương cấp n. Theo luật cập nhập thì: ( , , , )P Y v v Q Q rT1C= -to o o P P P P P"D D= - =t o to Lấy đạo hàm của P PTD CD ta được: ( )dt d P P P P P Y r P Y r r Y P T T T T T T T D CD D CD D CC D D = = = = = o o Nhân hai vế của phương trình (14) với rT ta được: ( )r H Q r r YDP r K r2 1 Y. T T T G r T D VT1 + =- - o ; E1 2 344 44 1 2 344 44 Trong đó: r K r V 0 0 0 0 T D " 2 2 2 1o Z [ \ ]]] ]]] Suy ra hệ ổn định theo tiêu chuẩn Lyapunov. 3. Kết quả ứng dụng thuật toán điều khiển cho robot RRT 3.1. Sơ đồ khối điều khiển robot RRT trong không gian Decac Sơ đồ mô tả như Hình 2. Giả sử vị trí ban đầu của tay kẹp robot RRT đang ở tọa độ x(0.768, 0.1560, 659) tương ứng với góc quay của khớp một và khớp 2 là (11.46o, 11.46o) và chiều dài thanh nối thứ ba là 0.3m. Đặt tọa độ vị trí tay kẹp robot mong muốn ISSN 2354-0575 Journal of Science and Technology30 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 trên hệ trục tọa độ O(x 0 , y 0 , z 0 ) là: (x d , y d , z d ) = (0.1, 0.3, 0.5) 3.2. Ứng dụng thuật toán điều khiển Đặt biến phụ: ( ( ))v J x L x x d d 1= + -- o (15) ( )v J x L x x Jv d d1= + - --o p o o o7 A (16) ( )r J Jq x L x x d d1= - + -- o o7 A (17) Với J là ma trận Jacobi của robot RRT được xác định từ vị trí của tay kẹp trong hệ trục tọa độ. ( , , ) ( ) ( ) ( ) O x y z x c c d q y c s d q z d s d q 0 0 0 1 2 2 3 2 1 2 3 1 2 2 3 = + = + = + + Z [ \ ]]] ]]]] (18) Suy ra: ( ) x s c d q 1 1 2 2 32 2 i =- + ; ( ) x c s d q 2 1 2 2 32 2 i =- + q x c c 3 1 22 2 = ; ( ) y c c d q 1 1 2 2 32 2 i = + ; ( ) y s s d q 2 2 1 2 32 2 i =- + ; q y s c 3 1 22 2 = ; z 0 12 2 i = ; ( ) z c d q 2 2 2 32 2 i = + ; q z s 3 22 2 = . Suy ra: ( ) ( ) ( ) ( ) ( ) J s c d q c c d q c s d q s s d q c d q c c s c s0 1 2 2 3 1 2 2 3 1 2 2 3 2 1 2 3 2 2 3 1 2 1 2 2 = - + + - + - + + J L KKKKKKK N P OOOOOOO ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) J c c d q s s d q s c c s d q s c d q c c s s d q c c d q c c s c d q c s d q s s s d q c s c c s s s c c c0 1 2 2 3 1 2 2 3 1 2 1 2 2 3 1 2 2 3 1 2 1 2 2 3 1 2 2 3 1 2 1 2 2 3 1 2 2 3 1 2 2 2 3 2 1 2 1 2 1 2 1 2 2 = - + + + - - + - + + + - + - + - + - - + + - - - +o J L KKKKKKK N P OOOOOOO (19) L là ma trận đường chéo xác định dương (3x3) , ,X x y z T=o o o o7 A với X Ji=o o Bộ điều khiển và luật cập nhập tham số là: T Hv Cv G K rd= + + +o (20) Với P T Y re T1=- -o hay ( , , , )P Y v v Q Q rT1C= -to o o Các tham số được cập nhập và đưa vào bộ điều khiển là: m; ; ; ;P m I I I T2 3 1 2 3= 8 BU U U Hình 2. Sơ đồ điều khiển robot RRT trong không gian Decac ISSN 2354-0575 Journal of Science and Technology31 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 Tài liệu tham khảo [1]. Nguyễn Mạnh Tiến, (2007), “Điều khiển Robot công nghiệp”, NXB KHKT, Hà Nội. [2]. Phạm Đăng Phước, (2006), “Robot công nghiệp”, NXB KHKT, Hà Nội. 3.3. Kết quả mô phỏng ứng dụng thuật toán cho robot RRT 3.3.1. Kết quả các đáp ứng của vị trí tay kẹp robot trong hệ trục tọa độ gốc Hình 3. Đáp ứng theo trục x Kd=[20 0 0; 0 20 0; 0 0 20] L=[10 0 0; 0 10 0; 0 0 10] Hình 4. Đáp ứng theo trục y Kd=[20 0 0; 0 20 0; 0 0 20] L=[10 0 0; 0 10 0; 0 0 10] Hình 5. Đáp ứng theo trục z Kd=[20 0 0; 0 20 0; 0 0 20] L=[10 0 0; 0 10 0; 0 0 10] Hình 6. Đáp ứng theo trục x, y, z Kd=[20 0 0; 0 20 0; 0 0 20] L=[10 0 0; 0 10 0; 0 0 10] 3.3.2. Đánh giá kết quả mô phỏng trên robot RRT Với kết quả mô phỏng thu được trong Hình 3, Hình 4, Hình 5, Hình 6 ta thấy - Tọa độ điểm tác động cuối của cánh tay máy bám theo tọa độ đặt trước (x d , y d , z d ) = (0.1, 0.3, 0.5) - Thời gian quá độ nhỏ (đều nhỏ hơn 0.5ms). - Độ quá điều chỉnh thấp. 4. Kết luận và đánh giá Bài báo trình bày tổng quan về ứng dụng thuật toán điều khiển thích nghi điều khiển chuyển động robot công nghiệp trong không gian Decac. Với kết quả thu được từ ứng dụng trên cánh tay robot RRT nhận thấy chất lượng điều khiển thu được khá tốt. Ưu điểm nổi bật của phương pháp này là hạn chế những ảnh hưởng của sự thay đổi các tham số động học của robot đến chất lượng chuyển động trong quá trình làm việc. Các tham số động học không cần xác định chính xác mà chỉ ước lượng một giá trị nào đó. Các tham số này sẽ được cập nhập thường xuyên bằng luật cập nhập tham số và được đưa vào bộ điều khiển. Điều này sẽ làm giảm sự ảnh hưởng của sự thay đổi các tham số động học của cánh tay robot trong quá trình làm việc. Ngoài ra, với thuật toán này có thể phát triển thêm ứng dụng mạng Neural trong việc nhận dạng sự thay đổi các tham số động học trong phương pháp này thì chất lượng điều khiển thu được sẽ tốt hơn. ISSN 2354-0575 Journal of Science and Technology32 Khoa học & Công nghệ - Số 9/Tháng 3 - 2016 [3]. Jean-Jacques, E.Slotine, Weiping Li, “On the Adaptive Control of RobotManipulator”, the international Journal of Robotics Research, 1987, page 147-157. [4]. Bernard Hodges, (1992), “Industrial Robotics”, Oxford Newnes. [5]. Prankl-Lewis, (2004), “Robot Manipulator Control Theory and Practice”, Marcel Dekker. [6]. Wesley E. Snyder, (1985), “Industrial Robots”, Computer Interfacing and Control, Prentice-Hall, New Jersey. RESEARCH, APPLY ADAPTIVE ALGORITHM TO CONTROL MOVEMENTS OF ROBOT MANIPULATOR IN DECAC SPACE Abstract: To improve the quality of industrial robot motion, the controller uses the control algorithm as sliding controller, PID offset gravity, exact linearization. However, the working conditions of industrial robots, the kinetic parameters such as changes in the weight of the robot arm to pick up objects, inertial torque changes affecting the motion of the robot. To mitigate and reduce the impact that the movement of the robot, using adaptive control algorithm with the aim to adapt with changes that kinetic parameters. Keywords: Robot control, Adaptive control, Control systems that have variability parameters.
File đính kèm:
 nghien_cuu_ung_dung_thuat_toan_thich_nghi_dieu_khien_chuyen.pdf
nghien_cuu_ung_dung_thuat_toan_thich_nghi_dieu_khien_chuyen.pdf

