Nghiên cứu tích hợp dẫn và điều khiển cho trực thăng không người lái
Máy bay trực thăng không người lái được
các nhà khoa học trong và ngoài nước hết
sức quan tâm. Giá trị và ứng dụng của nó
đã được khẳng định trên nhiều lĩnh vực
như quân sự, an ninh quốc phòng đến
phục vụ nghiên cứu khoa học, nông lâm
nghiệp, thương mại, vận chuyển, điện
ảnh. Vấn đề dẫn và điều khiển cho
TT-UAV liên tục được nghiên cứu phát
triển cả trong và ngoài nước, từ đơn giản
như điều khiển PID đến phức tạp như
logic mờ, mạng nơron, điều khiển tối ưu,
và điều khiển bền vững [3-4]. Tuy nhiên
vẫn cần tiếp tục nghiên cứu nhằm làm
phong phú thêm các thuật toán điều khiển
cho TT-UAV.
Máy bay trực thăng không người lái có
thể thực hiện các thao tác như bay lượn,
cất cánh và hạ cánh thẳng đứng. TT-UAV
là đối tượng có nhiều đầu ra nhiều đầu
vào, điều kiện bay phức tạp thay đổi liên
tục nên thiết kế hệ thống dẫn và điều
khiển cho TT-UAV là một công việc khó
khăn.

Trang 1

Trang 2

Trang 3

Trang 4
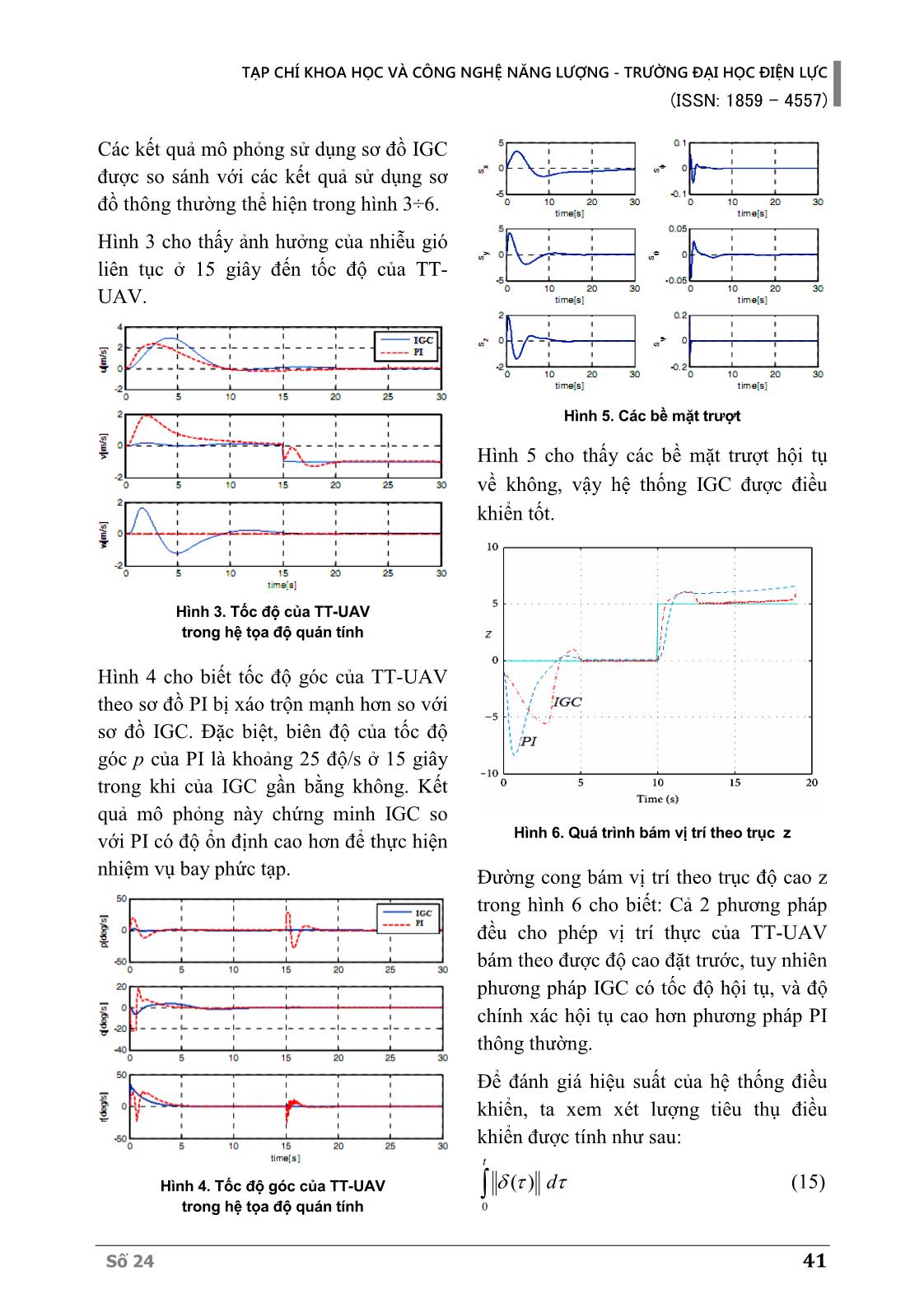
Trang 5

Trang 6

Trang 7

Trang 8
Tóm tắt nội dung tài liệu: Nghiên cứu tích hợp dẫn và điều khiển cho trực thăng không người lái

TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) Số 24 37 NGHIÊN CỨU TÍCH HỢP DẪN VÀ ĐIỀU KHIỂN CHO TRỰC THĂNG KHÔNG NGƯỜI LÁI RESEARCH ON INTEGRATED GUIDANCE AND CONTROL FOR UNMANNED HELICOPTER Đặng Tiến Trung1, Nguyễn Đức Việt2, Trần Xuân Tình2, Lê Ngọc Giang2* Trường Đại học Điện lực1, Học viện Phòng Không - Không quân2 Ngày nhận bài: 23/06/2020, Ngày chấp nhận đăng: 28/12/2020, Phản biện: PGS.TS. Nguyễn Quang Hoan Tóm tắt: Trong bài báo, luật dẫn và điều khiển tích hợp (IGC) được đề xuất cho máy bay trực thăng không người lái (TT-UAV). Trên cơ sở xem xét các đặc tính động của TT-UAV, tiến hành tổng hợp luật dẫn và ổn định tích hợp cho TT-UAV theo phương pháp điều khiển trượt. Các kết quả thu được chứng minh tính đúng đắn của phương pháp đề xuất, hệ thống làm việc ổn định, chính xác trong điều kiện có yếu tố bất định. Từ khóa: điều khiển phi tuyến, điều khiển tích hợp IGC, điều khiển trượt, trực thăng không người lái. Abstract: In this paper, the Integrated Guidance and Control (IGC) law is proposed for the Unmanned Helicopter (TT-UAV). On the basis of reviewing the dynamic characteristics of TT-UAV, the Integrated Guidance and Control law for TT-UAV by sliding mode control method has been conducted. The obtained results demonstrate the correctness of the proposed method, the system works stably and accurately under conditions of uncertainty. Keywords: nonlinear control, integrated guidance and control, sliding mode control, unmanned helicopter. 1. MỞ ĐẦU Máy bay trực thăng không người lái được các nhà khoa học trong và ngoài nước hết sức quan tâm. Giá trị và ứng dụng của nó đã được khẳng định trên nhiều lĩnh vực như quân sự, an ninh quốc phòng đến phục vụ nghiên cứu khoa học, nông lâm nghiệp, thương mại, vận chuyển, điện ảnh... Vấn đề dẫn và điều khiển cho TT-UAV liên tục được nghiên cứu phát triển cả trong và ngoài nước, từ đơn giản như điều khiển PID đến phức tạp như logic mờ, mạng nơron, điều khiển tối ưu, và điều khiển bền vững [3-4]. Tuy nhiên vẫn cần tiếp tục nghiên cứu nhằm làm phong phú thêm các thuật toán điều khiển cho TT-UAV. Máy bay trực thăng không người lái có thể thực hiện các thao tác như bay lượn, cất cánh và hạ cánh thẳng đứng. TT-UAV TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) 38 Số 24 là đối tượng có nhiều đầu ra nhiều đầu vào, điều kiện bay phức tạp thay đổi liên tục nên thiết kế hệ thống dẫn và điều khiển cho TT-UAV là một công việc khó khăn. Hệ thống điều khiển và dẫn của TT-UAV thường được thiết kế riêng biệt, vòng trong (vòng ổn định) có hằng số thời gian nhỏ hơn nhiều so với vòng ngoài (vòng dẫn Autopilots). Vòng ổn định bên trong sẽ nhận lệnh tạo ra từ vòng dẫn bên ngoài. Trong thiết kế của vòng dẫn, các đặc tính của bộ điều khiển không được xem xét trực tiếp, nên vòng dẫn có thể tạo ra các đầu vào điều khiển lớn đối với vòng ổn định, dễ gây ra sự mất ổn định của toàn bộ hệ thống. Vì lý do này, các tác giả đã tính toán tìm ra mô hình động học của TT-UAV phù hợp để tiến hành tổng hợp luật dẫn và ổn định tích hợp cho TT-UAV theo phương pháp điều khiển trượt. 2. MÔ HÌNH ĐỘNG HỌC CỦA TT-UAV Mô hình bài toán điều khiển: Theo [1] bộ điều khiển vòng trong được thiết kế để điều khiển các trạng thái nhanh bằng cách sử dụng đầu vào điều khiển u. Phương trình vi phân nhanh: M M M M x A x B u (1) Trong đó: T M T col lon lat tail x u v w p q r u (2) Vectơ trạng thái xM biểu thị các thành phần vận tốc (u, v, w) theo các trục X-Y-Z của hệ tọa độ đo, tốc độ góc (p, q, r) và các góc Euler (ø, θ, ψ) tương ứng. Vectơ đầu vào u biểu thị các tác động vào các cần điều khiển, gồm: δlat: góc quay cần điều khiển cyclic nghiêng, để tạo mômen làm cho thân máy bay nghiêng sang phải, sang trái theo chu kỳ một vòng quay (lateral cyclic); δlon: góc quay cần điều khiển cyclic dọc, để tạo mômen làm cho mũi máy bay hướng lên trên hoặc chúc xuống dưới theo chu kỳ một vòng quay (longitudinal cyclic); δtail: góc quay cần điều khiển collective cánh quạt đuôi, để thay đổi lực nâng của toàn bộ đĩa cánh quạt đuôi (tail rotor collective); δcol: góc cần điều khiển collective cánh quạt chính, để thay đổi lực nâng của toàn bộ đĩa cánh quạt chính (main rotor collecitve). Mô hình bài toán dẫn: Theo [1] bộ điều khiển vòng ngoài được thiết kế để điều khiển các trạng thái chậm. Phương trình vi phân chậm: M M M Mx A x B u (3) Xét quá trình bay của TT-UAV tiếp cận vị trí mong muốn như trong hình 1. Có hai hệ tọa độ: Hệ tọa độ quán tính (XI, YI, ZI) và hệ tọa độ đo (XB, YB, ZB). Các sai số dẫn trạng thái là: T G e e e e e ex x y z (4) TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) Số 24 39 Hình 1. TT-UAV tiếp cận vị trí mong muốn Trong đó, (xe, ye, ze) biểu thị sai số giữa vị trí thực tế (x, y, z) và vị trí mong muốn (xc, yc, zc) của TT-UAV. Nếu (x, y, z) và (xc, yc, zc) xác định trong hệ tọa độ quán tính, thì (xe, ye, ze) xác định trong hệ tọa độ đo. Tích hợp bài toán dẫn và điều khiển: Phương trình của hệ thống tích hợp cho cả 2 quá trình dẫn và điều khiển sẽ là phương trình vi phân cấp 2: ( , , , ) ( ) IGC IGC IGC c c IGC x f x x x x g x u (5) Trong đó, 6 1 6 4,f R g R Vectơ trạng thái của mô hình IGC: T M IGC T G x x x (6) Sơ đồ khối hệ thống tích hợp quá trình dẫn và điều khiển hiển thị trong hình 2. 3. THIẾT KẾ BỘ ĐIỀU KHIỂN TRONG CHẾ ĐỘ TRƯỢT Theo [2], bộ điều khiển trượt (SMC) được thiết kế để xây dựng các đầu vào điều khiển cho mô hình IGC. Bộ điều khiển trượt nổi tiếng là một phương pháp thiết kế điều khiển mạnh mẽ và phù hợp để xử lý các hệ thống phi tuyến với các sai số mô hình lớn, tham số không chắc chắn và nhiễu. SMC làm cho các sai số trạng thái dẫn hội tụ về giá trị 0. TT-UAV có g(.) của phương trình (5) là ma trận 6×4. Trong nghiên cứu này, phương pháp biến bù được áp dụng: Bằng cách bổ sung biến bù gs thành g và us thành u để tạo thành ma trận vuông, các đầu vào điều khiển có thể được xác định. Trong quá trình này, phương trình (5) có thể được viết lại như sau: ( , , , ) ( ) U IGC IGC IGC c c IGC a x f x x x x G x v (7) Trong đó, biến bù gs để tạo ma trận không khả nghịch G, và: , , , , , , c c c c c c c c c [ ]x y z u v w [ ]x y z u v w p q r , , , , , , , ,c c c c c c c c cx y z x y z x y z , ,r r rx y z Bộ điều khiển trượt (SMC) TT-UAV Bộ lọc bậc 2 Bộ truyền động Bộ tạo quỹ đạo Hình 2. Sơ đồ khối hệ thống tích hợp quá trình dẫn và điều khiển IY BY cX IZ IX X BX ( , , )e e e eX x y z Vị trí thực tế (x, y, z) Vị trí mong muốn ( , , z )c c cx y BZ TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) 40 Số 24 5 6 1 0 0 1 0 0 , 0 0 0 0 0 0 s s u g u u (8) 5 6 0 0 0 0 T s sv g u u u (9) Lưu ý rằng các biến bù u5 và u6 cần phải ước lượng. Bây giờ, chúng ta định nghĩa bề mặt trượt của bộ điều khiển SMC là: 1IGC IGCs x K x (10) Trong đó, K1 là một ma trận đường chéo với các phần tử dương. Dự kiến hệ thống IGC hoạt động trên bề mặt trượt của SMC, được định nghĩa là s = 0. Các đầu vào điều khiển được thiết kế bằng cách sử dụng hàm Lyapunov: 1 1 2 2 T TL s s v v (11) Trong đó, ˆv v v . Lưu ý rằng vˆ là giá trị ước lượng của v và ˆv v với giả định rằng v thay đổi chậm. Đạo hàm của hàm Lyapunov: 1 ˆ( ) ( ) T T T T a IGC L s s v v s f GU v K x v v (12) Theo định lý ổn định Lyapunov, các đầu vào điều khiển bổ sung được thiết kế để tạo ra đạo hàm thời gian của hàm Lyapunov dưới dạng bán xác định âm. Các đầu vào điều khiển được chọn là: 1 1 2ˆ sgn( ) a G U G f v K x K s (13) Trong đó, K2 là ma trận khuếch đại đầu vào (ma trận đường chéo với các phần tử dương). Bằng cách thế các đầu vào điều khiển bổ sung của phương trình (13) vào đạo hàm thời gian của hàm Lyapunov của phương trình (12), được: 2 2 ˆ ˆ( sgn( )) ( ) ˆ( ) T T T L s v v K s v v v s v K s (14) Cập nhật giá trị ước lượng vˆ : vˆ s (15) Đạo hàm của hàm Lyapunov: 2 0L K s (16) Do đạo hàm của Lyapunov là bán xác định âm, có thể kết luận rằng bề mặt trượt s=0 của phương trình (10) đạt được trong một thời gian hữu hạn. Điều này cho thấy luật dẫn có thể đạt được trong một thời gian hữu hạn. 4. MÔ PHỎNG Tiến hành mô phỏng sơ đồ điều khiển và dẫn tích hợp IGC, và so sánh với sơ đồ thông thường (điều khiển PI và dẫn PI). Mô phỏng được thực hiện bằng cách sử dụng MATLAB Simulink. Các tham số mô phỏng được chọn như sau: 2 1 2 9,81 m / s 0,2 0,2 1 1 10 10 10 0,2 0,2 1 1 10 10 10 g K diag K diag Trong mô phỏng, nhiệm vụ của TT-UAV bay từ điểm gốc (0, 0, 0) đến điểm mục tiêu (10, 10, 0), trong điều kiện có nhiễu gió liên tục thổi dọc theo trục Y trong hệ tọa độ đo với tốc độ 1 m/s tại 15 giây. TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) Số 24 41 Các kết quả mô phỏng sử dụng sơ đồ IGC được so sánh với các kết quả sử dụng sơ đồ thông thường thể hiện trong hình 3÷6. Hình 3 cho thấy ảnh hưởng của nhiễu gió liên tục ở 15 giây đến tốc độ của TT- UAV. Hình 3. Tốc độ của TT-UAV trong hệ tọa độ quán tính Hình 4 cho biết tốc độ góc của TT-UAV theo sơ đồ PI bị xáo trộn mạnh hơn so với sơ đồ IGC. Đặc biệt, biên độ của tốc độ góc p của PI là khoảng 25 độ/s ở 15 giây trong khi của IGC gần bằng không. Kết quả mô phỏng này chứng minh IGC so với PI có độ ổn định cao hơn để thực hiện nhiệm vụ bay phức tạp. Hình 4. Tốc độ góc của TT-UAV trong hệ tọa độ quán tính Hình 5. Các bề mặt trượt Hình 5 cho thấy các bề mặt trượt hội tụ về không, vậy hệ thống IGC được điều khiển tốt. Hình 6. Quá trình bám vị trí theo trục z Đường cong bám vị trí theo trục độ cao z trong hình 6 cho biết: Cả 2 phương pháp đều cho phép vị trí thực của TT-UAV bám theo được độ cao đặt trước, tuy nhiên phương pháp IGC có tốc độ hội tụ, và độ chính xác hội tụ cao hơn phương pháp PI thông thường. Để đánh giá hiệu suất của hệ thống điều khiển, ta xem xét lượng tiêu thụ điều khiển được tính như sau: 0 ( ) t d (15) TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) 42 Số 24 Lượng tiêu thụ điều khiển hay còn gọi là hàm chi phí, đây là một hàm chỉ tiêu chất lượng điều khiển. Mong muốn với mỗi lượng điều khiển đầu vào thì hệ thống tiêu thụ năng lượng ở mức tối thiểu. Lượng tiêu thụ điều khiển của 2 sơ đồ PI và IGC ứng với các đầu vào điều khiển được thống kê trong bảng so sánh hiệu suất 2 sơ đồ khi có nhiễu gió liên tục. Bảng thống kê cho thấy sơ đồ PI có lượng tiêu thụ điều khiển đầu vào gấp nhiều lần so với sơ đồ IGC. Vậy sơ đồ IGC đã cải thiện hiệu suất của TT-UAV. Bảng so sánh hiệu suất 2 sơ đồ khi có nhiễu gió liên tục Đầu vào điều khiển JIGC JPI Tỷ lệ col 0,07 0,01 7:1 lon 0,10 0,15 1:1,5 cot 0,02 0,21 1:10,5 Đầu vào điều khiển JIGC JPI Tỷ lệ tail 0,02 0,12 1:6 Tổng 0,21 0,49 1:2,3 5. KẾT LUẬN Bài báo đề xuất áp dụng tích hợp hệ thống dẫn và điều khiển cho TT-UAV. Bộ điều khiển chế độ trượt được bổ sung với các biến bù được sử dụng để thiết kế hệ thống IGC. Kết quả mô phỏng cho thấy sơ đồ IGC đề xuất cho hiệu suất tốt hơn so với phương pháp thông thường. Sơ đồ IGC cung cấp phản ứng nhanh, mạnh mẽ đối với nhiễu bên ngoài và lượng tiêu thụ điều khiển đầu vào nhỏ. Kết quả nghiên cứu này là tiền đề để nhóm tác giả tiến hành hiện thực hóa tổng hợp luật dẫn và ổn định tích hợp cho TT- UAV theo phương pháp điều khiển trượt. TÀI LIỆU THAM KHẢO [1] Pedro V.M. Simplicio, "Helicopter Nonlinear Flight Control: An Acceleration Measurements-based Approach using Incremental Nonlinear Dynamic Inversion", Master of Science Thesis, Faculty of Aerospace Engineering, Delft University of Technology, August 23, 2011. [2] Lee, D., Kim, H., Sastry, S., “Feedback Linearization vs. Adaptive Sliding Mode Control for a Quadrotor Helicopter”, International Journal of Control, Automation, and Systems, Vol. 7, No. 3, 2009, pp. 419-428. [3] V.G. Nair, M.V. Dileep, and V.I. George, “Aircraft Yaw Control System Using LQR and Fuzzy Logic Controller,” International Journal of Computer Applications, vol. 45, no. 9, pp. 25–30, 2012. [4] H. Yan, X. Wang, B. Yu, H. Ji, “Adaptive Integrated Guidance and Control based on Backstepping and Input-to-State Stability,” Asian Journal of Control, vol. 16, no. 2, pp. 602–608, 2014. TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) Số 24 43 Giới thiệu tác giả: Tác giả Đặng Tiến Trung tốt nghiệp đại học chuyên ngành điện - tự động hóa tại Trường Đại học Bách khoa Hà Nội năm 2004; nhận bằng Tiến sĩ năm 2019 tại Học viện Kỹ thuật quân sự. Tác giả hiện là giảng viên Khoa Kỹ thuật điện, Trường Đại học Điện lực. Lĩnh vực nghiên cứu: ứng dụng các giải pháp điều khiển hiện đại trong hệ thống điện. Tác giả Trần Xuân Tình tốt nghiệp đại học chuyên ngành điện tử, nhận bằng Thạc sĩ chuyên ngành tự động hóa năm 2013. Tác giả hiện là giảng viên Bộ môn Kỹ thuật điện, Học viện Phòng không - Không quân. Lĩnh vực nghiên cứu: ứng dụng các giải pháp điều khiển hiện đại trong hệ truyền động điện. Tác giả Lê Ngọc Giang nhận bằng Thạc sĩ chuyên ngành tự động hóa và điều khiển các thiết bị bay năm 2010 tại Học viện Kỹ thuật quân sự, nhận bằng Tiến sĩ chuyên ngành hệ thống điện và tự động hóa năm 2015 tại Đại học Vũ Hán, Trung Quốc. Tác giả hiện là Chủ nhiệm Bộ môn Đo lường, Học viện Phòng không - Không quân. Lĩnh vực nghiên cứu: thiết kế hệ thống điều khiển tự động cho các thiết bị bay và hệ thống năng lượng gió. Tác giả Nguyễn Đức Việt nhận bằng Thạc sĩ chuyên ngành kỹ thuật điều khiển và tự động hóa năm 2019 tại Học viện Kỹ thuật quân sự. Hiện nay, tác giả là giảng viên Bộ môn Kỹ thuật điện, Học viện Phòng không - Không quân. Lĩnh vực nghiên cứu: thiết kế các hệ thống đo lường và điều khiển. TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC (ISSN: 1859 - 4557) 44 Số 24
File đính kèm:
 nghien_cuu_tich_hop_dan_va_dieu_khien_cho_truc_thang_khong_n.pdf
nghien_cuu_tich_hop_dan_va_dieu_khien_cho_truc_thang_khong_n.pdf

