Nghiên cứu khả năng áp dụng công thức kinh nghiệm để tính toán mức độ xói lở bờ sông ở đồng bằng sông Cửu Long – Thí điểm tại đoạn xói lở bờ sông Hậu ở Long Xuyên, tỉnh An Giang

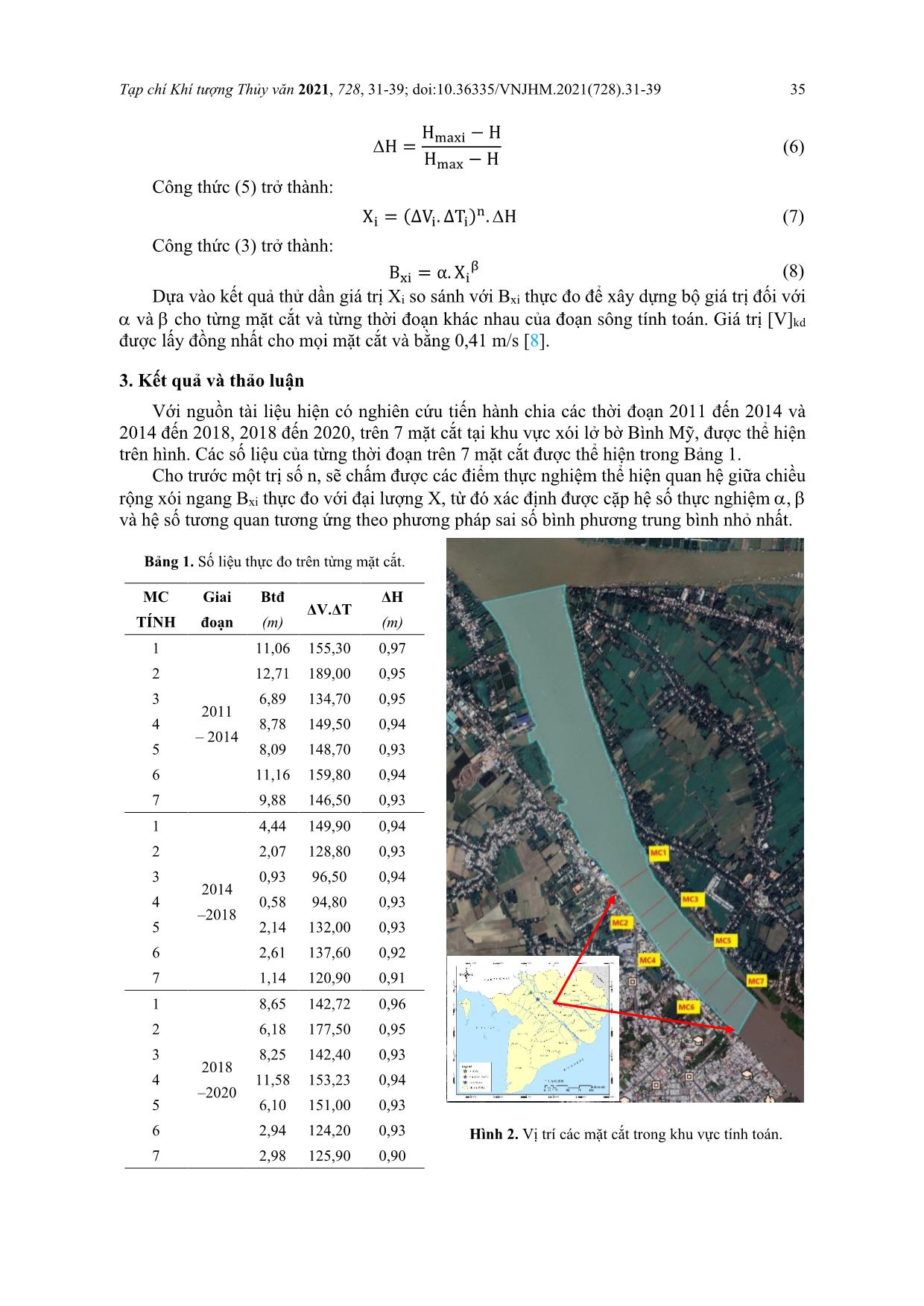
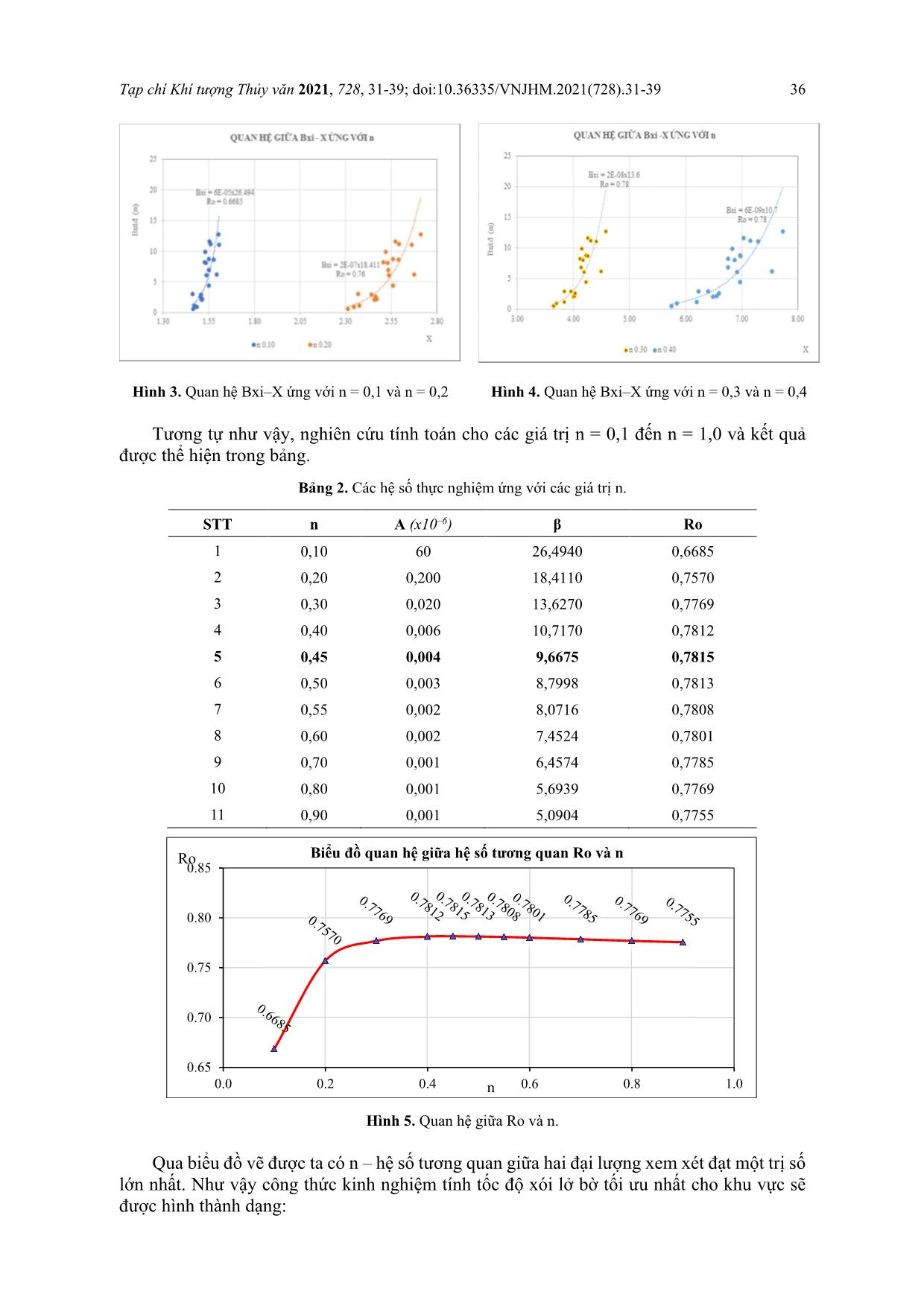
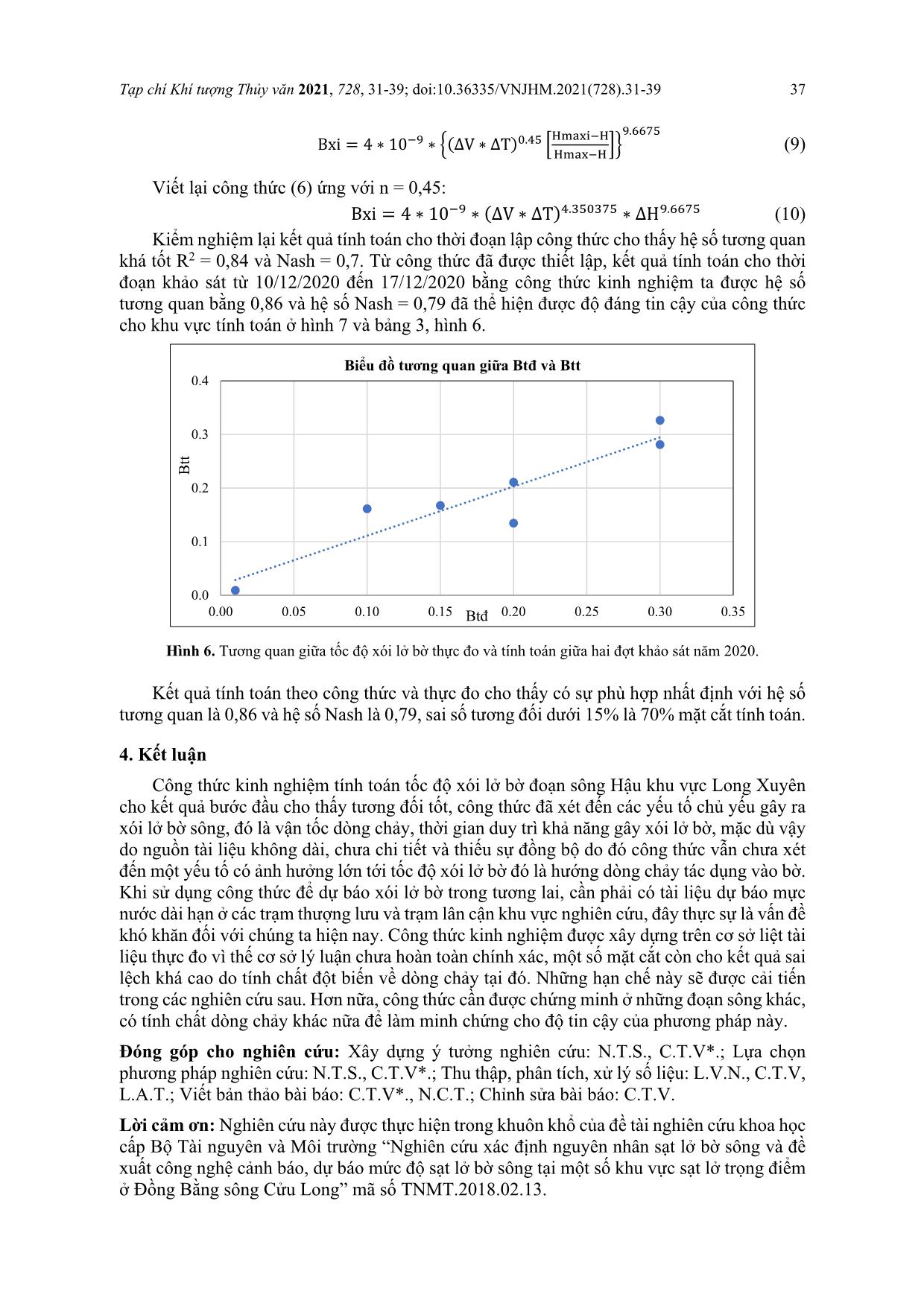
 Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39  
Bài báo khoa học 
Nghiên cứu khả năng áp dụng công thức kinh nghiệm để tính 
toán mức độ xói lở bờ sông ở đồng bằng sông Cửu Long – Thí 
điểm tại đoạn xói lở bờ sông Hậu ở Long Xuyên, tỉnh An Giang 
Cấn Thu Văn1*, Nguyễn Thanh Sơn2, Ngô Chí Tuấn2, Lưu Văn Ninh3, Cấn Thế Việt4, 
Lục Anh Tuấn1 
1 Trường Đại học Tài nguyên và Môi trường TP.HCM, 236B Lê Văn Sỹ, phường 1, quận 
Tân Bình, TP.HCM; ctvan@hcmunre.edu.vn; lucanhtuan1103@gmail.com 
2 Trường Đại học Khoa học Tự nhiên–ĐHQGHN, 334 Nguyễn Trãi, Thanh Xuân, Hà Nội; 
sonnt.vnu.hus.edu.vn; ngochituan@gmail.com 
3 Đài Khí tượng Thủy văn tỉnh An Giang, 64 Tôn Đức Thắng, thành phố Long Xuyên, tỉnh 
An Giang; luuninhtv@gmail.com 
4 Viện Môi trường Thủy lợi–Đại học Thủy lợi, số 02 Trường Sa, phường 17, quận Bình 
Thạnh, TP.HCM; theviet8387@gmail.com 
*Tác giả liên hệ: ctvan@hcmunre.edu.vn; Tel.: +84–983738347 
Ban Biên tập nhận bài: 12/4/2021; Ngày phản biện xong: 8/6/2021; Ngày đăng bài: 
25/8/2021 
Tóm tắt: Đồng bằng sông Cửu Long (ĐBSCL) là nơi sinh sống của gần 20 triệu người và là 
vùng canh tác nông nghiệp lớn nhất nước ta. Trong bối cảnh biến đổi khí hậu ngày một rõ rệt 
cùng với sự can thiệp quá mức của con người vào thiên nhiên, hiện tượng sạt lở bờ sông và 
đã và đang là mối đe dọa đến cuộc sống của người dân nơi đây. Ở ĐBSCL hiện có 406 đoạn 
sạt lở, với tổng chiều dài 891 km, trong đó An Giang được đánh giá là một trong những địa 
phương bị ảnh hưởng nghiêm trọng nhất do sạt lở bờ sông. Hiện có nhiều phương pháp được 
sử dụng để đánh giá, dự báo mức độ sạt lở bờ sông ở những khu vực cụ thể, như là: phương 
pháp phân tích tài liệu thực đo; mô hình vật lý; mô hình toán; công thức kinh nghiệm. Trong 
nghiên cứu này sử dụng công thức kinh nghiệm để tính toán thử nghiệm mức độ sạt lở cho 
đoạn sông Hậu ở thành phố Long Xuyên, tỉnh An Giang. Kết quả tính toán theo công thức 
cho thấy có sự phù hợp nhất định vớ kết quả thực đo, với hệ số tương quan là 0,86 và hệ số 
Nash là 0,79, sai số tương đối dưới 15% là 70% mặt cắt tính toán. Điều này bước đầu đã cho 
thấy khả năng có thể áp dụng công thức để thiết lập hệ số và tính toán cho các vùng khác 
thuộc bờ sông Hậu và ĐBSCL. 
Từ khóa: Xói lở bờ sông; ĐBSCL; Công thức kinh nghiệm tính xói lở bờ. 
1. Đặt vấn đề 
Đồng bằng sông Cửu Long (ĐBSCL) thuộc hạ lưu sông Mê Công giữ vai trò quan trọng 
trong phát triển kinh tế, nhất là kinh tế nông nghiệp, thủy sản đối với cả nước, chiếm 55% sản 
lượng lúa, 90% sản lượng gạo xuất khẩu. ĐBSCL với hơn 700 km bờ biển, chiếm 70% diện 
tích nuôi trồng thủy sản, ... Tuy nhiên, do ở cuối nguồn nước và trong bối cảnh biến đổi khí 
hậu, lại chịu hậu quả của các công trình thủy điện phía thượng lưu nên ĐBSCL thường xuyên 
phải đối mặt với nguy cơ: suy giảm và thay đổi dòng chảy, suy giảm lượng phù sa từ thượng 
lưu xuống hạ lưu, suy giảm khả năng điều tiết nguồn nước giữa mùa mưa và mùa khô sẽ gây 
nên những tai biến bất thường như: hạn hán, lũ lụt, xâm nhập mặn, ô nhiễm nguồn nước, nước 
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 32 
biển dâng, đặc biệt là hiện tượng xói mòn, sạt lở nghiêm trọng trong những năm gần đây 
[1]. 
Hình 1. Bản đồ khu vực ĐBSCL [2]. 
Bồi lắng, xói lở là một quá trình tự nhiên và xảy ra một cách liên tục ở hầu hết tất cả các 
con sông trên lục địa. Tuy nhiên, quá trình này, đặc biệt là sạt lở bờ sông, trở nên đáng quan 
tâm là khi nó gây ra thiệt hại về đất đai, tài nguyên, tài sản của con người. Xói lở là một quá 
trình tương tác đất nước xảy ra thường xuyên nên trong suốt thời gian qua rất nhiều nhà khoa 
học trên thế giới đã tập trung nghiên cứu hiện tượng bồi lắng, sạt lở của các dòng sông, đặc 
biệt là các con sông lớn [3]. Hướng nghiên cứu thứ nhất là địa mạo học sông ngòi, chuyên 
nghiên cứu về sự biến động hình dạng của con sông theo thời gian và không gian. Những sự 
thay đổi này có thể là về: kích thước, hình dạng, thành phần vật liệu đáy, độ đốc, hình dạng 
trên mặt bằng [4]. Hướng thứ hai, các nhà khoa học quan tâm tới là sự hiểu biết các cơ chế: 
sạt lở; vận chuyển và bồi lắng của bùn cát do dòng chảy trong sông, từ đó phát triển các 
phương pháp dự đoán các quá trình diễn biến lòng sông. Đây là tiếp cận theo hướng thủy 
thạch động lực học sông ngòi [5]. 
Đặc biệt trong những thập kỷ gần đây, sự ra đời của hệ thống máy tính tốc độ cao và rất 
nhiều đóng góp của các nhà khoa học khác trên thế giới, các phương trình mô tả sự vận động 
phức tạp của các con sông và trầm tích đã được giải quyết để phát triển các phương pháp tính 
toán cao trình đáy sông trong dòng chảy không đều. Đồng thời, các nghiên cứu bằng mô hình 
trong phòng thí nghiệm kết hợp với các số liệu đo đạc ngoài hiện trường cũng đã và đang 
được thu thập để nghiên cứu một số vấn đề chưa được làm sáng tỏ về mặt lý luận. Ngày nay, 
với sự phát triển mạnh mẽ của khoa học kỹ thuật, các nhà khoa học trên th ... a bờ sông. 
Theo Pôpôp trong [23–24], cũng đề cập tới ba yếu tố chính nêu trên trong công thức kinh 
nghiệm tính tốc độ xói lở bờ sông của mình: 
B =
α. F
L. T

H − H
H − H


 (2) 
Trong đó Bxi là tốc độ xói lở ngang (m/năm) tại mặt cắt i; F là diện tích khối đất bờ bị xói 
lở trong khoảng thời gian T năm (m2); L là chiều dài đường bờ sạt lở của từng giai đoạn (m); 
T là thời gian xói lở (năm); Hmaxi là độ sâu lớn nhất tại mặt cắt tính toán thứ i (m); Hmax là độ 
sâu lớn nhất của đoạn xói lở nghiên cứu (m); H là độ sâu ổn định (tại mặt cắt quá độ) (m); , 
 là các hệ số thực nghiệm. 
Nhìn chung các công thức kinh nghiệm của các tác giả nêu trên đều có khả năng áp dụng 
tính tốc độ xói lở bờ sông Cửu Long, khi các hệ số thực nghiệm được xác định từ tài liệu thực 
đo tại vị trí xem xét. Tuy vậy khi áp dụng những công thức này vào các vị trí cụ thể sẽ có sai 
số cao và các công thức chưa đề cập tới khả năng và thời gian duy trì khả năng của dòng chảy 
gây ra xói lở bờ sông. 
Khảo sát thực tế cho thấy đại lượng 


 trong công thức PôPốp quan hệ khá chặt chẽ với 
tích số giữa khả năng và thời gian duy trì khả năng của dòng chảy gây xói lở. Bởi vậy, trong 
nghiên cứu này đã thay đại lượng 


 trong (2) bằng đại lượng Vi, Ti [8]. 
Như vậy công thức kinh nghiệm được đề xuất có dạng: 
B = α. (∆V. ∆T)
. 
H − H
H − H


 (3) 
Trong đó ∆ =  − []; Vi là số gia vận tốc, biểu thị khả năng dòng chảy gây xói 
lòng dẫn tại mặt cắt thứ i; Vi là vận tốc trung bình tại mặt cắt thứ i (m/s); [V]kd là vận tốc khởi 
động của vật liệu cấu tạo lòng dẫn; Ti là thời gian duy trì vận tốc dòng chảy có vận tốc lớn 
hơn vận tốc khởi động của vật liệu cấu tạo lòng dẫn tại mặt cắt thứ i; , ,  là các hệ số thực 
nghiệm, được xác định trên cơ sở tài liệu thực đo nhiều năm. 
Công thức (3), bao hàm 3 hệ số thực nghiệm cần xác định , , , với cách tính thông 
thường khó khăn để tính toán, vì thế công thức sẽ được viết dưới một dạng khác: 
B = α. (∆V. ∆T)
. 
H − H
H − H


 (4) 
Trong đó n =


 Với cách viết biểu thức dưới dạng (4), hai hệ số thực nghiệm ,  sẽ 
được xác định theo phương pháp sai số bình phương trung bình nhỏ nhất khi n cho trước. 
Ứng với mỗi trị số n cho trước sẽ xác định được hệ số tương quan giữa chiều rộng xói 
ngang Bxi tính toán trong các giai đoạn tính: 
X = (∆V. ∆T)
. 


 (5) 
Hai hệ số thực nghiệm cần xác định là hai hệ số tương ứng với trường hợp hệ số tương 
quan lớn nhất. Thiết lập công thức tính xói lở cho khu vực ở Long Xuyên, An Giang: 
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 35 
 H =
H − H
H − H
 (6) 
Công thức (5) trở thành: 
X = (∆V. ∆T)
. H (7) 
Công thức (3) trở thành: 
B = α. X
 (8) 
Dựa vào kết quả thử dần giá trị Xi so sánh với Bxi thực đo để xây dựng bộ giá trị đối với 
 và  cho từng mặt cắt và từng thời đoạn khác nhau của đoạn sông tính toán. Giá trị [V]kd 
được lấy đồng nhất cho mọi mặt cắt và bằng 0,41 m/s [8]. 
3. Kết quả và thảo luận 
Với nguồn tài liệu hiện có nghiên cứu tiến hành chia các thời đoạn 2011 đến 2014 và 
2014 đến 2018, 2018 đến 2020, trên 7 mặt cắt tại khu vực xói lở bờ Bình Mỹ, được thể hiện 
trên hình. Các số liệu của từng thời đoạn trên 7 mặt cắt được thể hiện trong Bảng 1. 
Cho trước một trị số n, sẽ chấm được các điểm thực nghiệm thể hiện quan hệ giữa chiều 
rộng xói ngang Bxi thực đo với đại lượng X, từ đó xác định được cặp hệ số thực nghiệm ,  
và hệ số tương quan tương ứng theo phương pháp sai số bình phương trung bình nhỏ nhất. 
Bảng 1. Số liệu thực đo trên từng mặt cắt. 
MC 
TÍNH 
Giai 
đoạn 
Btđ 
(m) 
ΔV.ΔT 
ΔH 
(m) 
1 
2011 
– 2014 
11,06 155,30 0,97 
2 12,71 189,00 0,95 
3 6,89 134,70 0,95 
4 8,78 149,50 0,94 
5 8,09 148,70 0,93 
6 11,16 159,80 0,94 
7 9,88 146,50 0,93 
1 
2014 
–2018 
4,44 149,90 0,94 
2 2,07 128,80 0,93 
3 0,93 96,50 0,94 
4 0,58 94,80 0,93 
5 2,14 132,00 0,93 
6 2,61 137,60 0,92 
7 1,14 120,90 0,91 
1 
2018 
–2020 
8,65 142,72 0,96 
2 6,18 177,50 0,95 
3 8,25 142,40 0,93 
4 11,58 153,23 0,94 
5 6,10 151,00 0,93 
6 2,94 124,20 0,93 
7 2,98 125,90 0,90 
Hình 2. Vị trí các mặt cắt trong khu vực tính toán. 
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 36 
Hình 3. Quan hệ Bxi–X ứng với n = 0,1 và n = 0,2 Hình 4. Quan hệ Bxi–X ứng với n = 0,3 và n = 0,4 
Tương tự như vậy, nghiên cứu tính toán cho các giá trị n = 0,1 đến n = 1,0 và kết quả 
được thể hiện trong bảng. 
Bảng 2. Các hệ số thực nghiệm ứng với các giá trị n. 
STT n Α (x10–6) β Ro 
1 0,10 60 26,4940 0,6685 
2 0,20 0,200 18,4110 0,7570 
3 0,30 0,020 13,6270 0,7769 
4 0,40 0,006 10,7170 0,7812 
5 0,45 0,004 9,6675 0,7815 
6 0,50 0,003 8,7998 0,7813 
7 0,55 0,002 8,0716 0,7808 
8 0,60 0,002 7,4524 0,7801 
9 0,70 0,001 6,4574 0,7785 
10 0,80 0,001 5,6939 0,7769 
11 0,90 0,001 5,0904 0,7755 
Hình 5. Quan hệ giữa Ro và n. 
Qua biểu đồ vẽ được ta có n – hệ số tương quan giữa hai đại lượng xem xét đạt một trị số 
lớn nhất. Như vậy công thức kinh nghiệm tính tốc độ xói lở bờ tối ưu nhất cho khu vực sẽ 
được hình thành dạng: 
0.65
0.70
0.75
0.80
0.85
0.0 0.2 0.4 0.6 0.8 1.0
Ro
n
Biểu đồ quan hệ giữa hệ số tương quan Ro và n
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 37 
Bxi = 4 ∗ 10 ∗ (∆V ∗ ∆T). 



.
 (9) 
Viết lại công thức (6) ứng với n = 0,45: 
Bxi = 4 ∗ 10 ∗ (∆V ∗ ∆T). ∗ ∆H. (10) 
Kiểm nghiệm lại kết quả tính toán cho thời đoạn lập công thức cho thấy hệ số tương quan 
khá tốt R2 = 0,84 và Nash = 0,7. Từ công thức đã được thiết lập, kết quả tính toán cho thời 
đoạn khảo sát từ 10/12/2020 đến 17/12/2020 bằng công thức kinh nghiệm ta được hệ số 
tương quan bằng 0,86 và hệ số Nash = 0,79 đã thể hiện được độ đáng tin cậy của công thức 
cho khu vực tính toán ở hình 7 và bảng 3, hình 6. 
Hình 6. Tương quan giữa tốc độ xói lở bờ thực đo và tính toán giữa hai đợt khảo sát năm 2020. 
Kết quả tính toán theo công thức và thực đo cho thấy có sự phù hợp nhất định với hệ số 
tương quan là 0,86 và hệ số Nash là 0,79, sai số tương đối dưới 15% là 70% mặt cắt tính toán. 
4. Kết luận 
Công thức kinh nghiệm tính toán tốc độ xói lở bờ đoạn sông Hậu khu vực Long Xuyên 
cho kết quả bước đầu cho thấy tương đối tốt, công thức đã xét đến các yếu tố chủ yếu gây ra 
xói lở bờ sông, đó là vận tốc dòng chảy, thời gian duy trì khả năng gây xói lở bờ, mặc dù vậy 
do nguồn tài liệu không dài, chưa chi tiết và thiếu sự đồng bộ do đó công thức vẫn chưa xét 
đến một yếu tố có ảnh hưởng lớn tới tốc độ xói lở bờ đó là hướng dòng chảy tác dụng vào bờ. 
Khi sử dụng công thức để dự báo xói lở bờ trong tương lai, cần phải có tài liệu dự báo mực 
nước dài hạn ở các trạm thượng lưu và trạm lân cận khu vực nghiên cứu, đây thực sự là vấn đề 
khó khăn đối với chúng ta hiện nay. Công thức kinh nghiệm được xây dựng trên cơ sở liệt tài 
liệu thực đo vì thế cơ sở lý luận chưa hoàn toàn chính xác, một số mặt cắt còn cho kết quả sai 
lệch khá cao do tính chất đột biến về dòng chảy tại đó. Những hạn chế này sẽ được cải tiến 
trong các nghiên cứu sau. Hơn nữa, công thức cần được chứng minh ở những đoạn sông khác, 
có tính chất dòng chảy khác nữa để làm minh chứng cho độ tin cậy của phương pháp này. 
Đóng góp cho nghiên cứu: Xây dựng ý tưởng nghiên cứu: N.T.S., C.T.V*.; Lựa chọn 
phương pháp nghiên cứu: N.T.S., C.T.V*.; Thu thập, phân tích, xử lý số liệu: L.V.N., C.T.V, 
L.A.T.; Viết bản thảo bài báo: C.T.V*., N.C.T.; Chỉnh sửa bài báo: C.T.V. 
Lời cảm ơn: Nghiên cứu này được thực hiện trong khuôn khổ của đề tài nghiên cứu khoa học 
cấp Bộ Tài nguyên và Môi trường “Nghiên cứu xác định nguyên nhân sạt lở bờ sông và đề 
xuất công nghệ cảnh báo, dự báo mức độ sạt lở bờ sông tại một số khu vực sạt lở trọng điểm 
ở Đồng Bằng sông Cửu Long” mã số TNMT.2018.02.13. 
0.0
0.1
0.2
0.3
0.4
0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35
B
tt
Btđ
Biểu đồ tương quan giữa Btđ và Btt
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 38 
Lời cam đoan: Tập thể tác giả cam đoan bài báo này là công trình nghiên cứu của tập thể tác 
giả, chưa được công bố ở đâu, không được sao chép từ những nghiên cứu trước đây, không có 
sự tranh chấp lợi ích trong nhóm tác giả. 
Tài liệu tham khảo 
1. Van, C.T.; Duong, P.T.T.; Nga, Đ.T.; Ninh, L.V. Study on assessing the impact of 
climate change (temperature and rainfall) on rice yield in the Long Xuyen 
Quadrangle region (LXQR) – Vietnam. VN J. Hydrometeorol. 2021, 7, 20–31. 
doi:10.36335/VNJHM.2021(7).20–31. 
2. Viện Khoa học Thủy lợi Miền Nam, Đánh giá kết quả thực hiện “Định hướng Chiến 
lược phát triển Thủy lợi Việt Nam” giai đoạn 2009 đến 2015 Vùng Đồng bằng sông 
Cửu Long. Báo cáo Dự án Rừng và Đồng bằng Việt Nam, 2016. 
3. Bravard, J.P.; Petit, F. Geomorphology of Streams and Rivers. Encycl. Inland 
Waters 2009, 387–395. https://doi.org/10.1016/B978-012370626-3.00043-0. 
4. Ian Reid, James C Bathurst, Paul Carling, Des E Walling, 1997, book: Applied 
fluvial geomorphology for river engineering and management, Chapter Sediment 
erosion, transport, and deposition, (pp.95-135), John Wiley and Sons 
5. Simon, A.; Collison, A.J.C. Quantifying the mechanical and hydrologic effects of 
riparian vegetation on streambank stability. Earth Surf. Processes Landforms 2002, 
27, 527–546. 
6. Winterbottom, S.J.; Gilvear, D.J. A GIS-based approach to mapping probabilities of 
river bank erosion: regulated river Tummel, Scotland. Regul. Rivers: Res. Manage.
 2000, 16, 127–140. 
7. Blazejewski, R.; Pilarczyk, K.W.; Przedwojski, B. River Training Techniques: 
Fundamentals, Design and Applications, Rotterdam, 1995. 
8. Hùng, L.M. Nghiên cứu dự báo xói lở, bồi lắng lòng dẫn và đề xuất các biện pháp 
phòng chống cho hệ thống sông đồng bằng sông Cửu Long. Báo cáo tổng hợp đề tài 
KC08–15/01–05, 2004. 
9. Stephen, H.S.; Jia, Y. Simulation of sediment transport and channel morphology 
change in large river systems us–china workshop on advanced computational 
modelling in hydroscience & engineering, September 19–21, Oxford, Mississippi, 
USA, 2002. 
10. Wu, W.M. CCHE2D Sediment Transport Model. Technical Report No. NCCHE–
TR–2001– 3, National Center for Computational Hydroscience and Engineering, 
The University of Mississippi, 2001. 
11. Springer, G.S.; Rowe, H.D.; Hardt, B.; Cociana, F.G.; Edwards, R.L.; Cheng, H. 
Climate driven changes in river channel morphology and base level during the 
holocene and late pleistocene of Southeastern West Virginia. J. Cave Karst Stud. 
2009, 71(2), 121–129. 
12. Rosgen, D.L. A practical method of computing streambank erosion rate. Proceedings 
of the Seventh Federal Interagency Sedimentation Conference 2001, 2, 9–15. 
13. Nga, T.N.Q.; Thuận, L.T.; Hoài, H.C.; Bảy, N.T. Nghiên cứu ứng dụng mô hình toán 
và công thức kinh nghiệm đánh giá sự phát triển của hố xói sâu hạ lưu sông Hậu và 
sông Vàm Nao. Tạp chí Khí tượng Thủy văn 2020, 5, 1–10. 
14. Hùng, L.M.; Hoằng, T.B.; Khang, N.D.; Anh, T.T. Kết quả ứng dụng mô hình 
SWAT trong tính toán xói lở bề mặt lưu vực hạ lưu sông Mekong. Tạp chí Khoa học 
và Công nghệ Thủy lợi 2012, 12, 25–32. 
15. Hùng, L.M.; Ngọc, Đ.T.B. Công thức kinh nghiệm tính tốc độ xói lở bờ đoạn sông 
Tiền khu vực Thường Phước, tỉnh Đồng Tháp. Tạp chí Nông nghiệp và Phát triển 
nông thôn 2004, 06, 787-796. 
Tạp chí Khí tượng Thủy văn 2021, 728, 31-39; doi:10.36335/VNJHM.2021(728).31-39 39 
16. Giáp, N.Đ.; Hậu, L.P. Xây dựng công thức kinh nghiệm tính toán hiệu quả bồi lắng 
của hệ thống đảo chiều hoàn lưu trên sông Dinh tại Phan Rang. 
17. Hải, H.Q.; Trinh, V.T.M. Tương quan xói lở – Bồi tụ một số khu vực lòng sông Tiền, 
sông Hậu. Tạp chí các khoa học về Trái đất 2011, 33(1), 37–44. 
18. Dinh Cong San, “Research on river bed erosion and sedimentation prediction by 
MIKE21C model at Tan Chau-Hong Ngu area, in the Mekong River”, Proceedings 
of the International Symposium on Sustainable Development in the Mekong River 
basin, 2005, 188-195. 
19. Hoàng, T.P.; Hùng, P.T. Mối quan hệ giữa khai thác cát với biến động bờ sông Tiền 
tại tỉnh Đồng Tháp. J. Sci. 2016, 12(4), 92–103. 
20. Ninh, L.V. Nghiên cứu xây dựng cơ sở dữ liệu khí tượng thủy văn tỉnh An Giang 
trong bối cảnh biến đổi khí hậu. Báo cáo tổng hợp đề tài KHCN cấp tỉnh, 2018. 
21. Ninh, L.V.; Giám, N.M. Đặc điểm khí hậu An Gang. Tạp chí Khí tượng Thủy văn 
2017, 648, 18–26. 
22. Ibad–Zade Iu. A., Kiacbeili T. H. Biến hình lòng sông, Baku, 1966. 
23. Hùng, L.M.; Sản, Đ.C. Xói lở bờ sông Cửu Long và giải pháp phòng tránh cho các 
khu vực trọng điểm, Nhà xuất bản Nông nghiệp, 2002. 
Study on the applicability of empirical formulas to calculate 
riverbank erosion in the Mekong Delta – Pilot at Hau River bank 
in Long Xuyen, An Giang Province 
Can Thu Van1*, Nguyen Thanh Son2, Ngo Chi Tuan2, Luu Van Ninh3, Can The Viet4, 
Luc Anh Tuan1 
1 HCMC University of Natural Resources and Environment, 236B Le Van Sy, ward 1, Tan 
Binh district, HCM city; ctvan@hcmunre.edu.vn; lucanhtuan1103@gmail.com 
2 Hanoi University of Science–VNU, 334 Nguyen Trai, Thanh Xuan, Ha Noi; 
sonnt.vnu.hus.edu.vn; ngochituan@gmail.com 
3 Hydro–Meteorology Center of An Giang Province, 64 Ton Duc Thang, Long Xuyen city, 
An Giang province; luuninhtv@gmail.com 
4 Environment and Water resources Institute–Thuyloi University, 02 Truong Sa, ward 17, 
Binh Thanh district, HCM city; theviet8387@gmail.com 
Abstract: The Mekong Delta is home to nearly 20 million people and is the largest 
agricultural area in Vietnam. Climate change is increasingly fierce and complex, along with 
excessive human intervention in nature, which are the causes of riverbank erosion and have 
been and are a threat to the lives of people here. The aggregated data shows that there are 
406 landslide sections in the Mekong Delta, with a total length of 891 km, of which An 
Giang is assessed as one of the localities most severely affected by riverbank erosion. There 
are many methods used to assess and predict riverbank erosion in specific areas, such as: 
analysis of measured data; physical model; mathematical model; experience formula. This 
study use empirical formula to calculate the erosion level for Hau river bank in Long Xuyen 
city, An Giang Province. The calculation results according to the formula and the actual 
measurements show that there is a certain agreement with the correlation coefficient of 0.86 
and the Nash coefficient of 0.79, relative error less than 15% is 70% of calculated cross–
section. Such results, initially showed the possibility of applying the formula to set up 
coefficients and calculate for other regions of the Hau River and Mekong Delta. 
Keywords: Riverbank erosion; Mekong Delta; Empirical formula for calculating bank 
erosion.