Nghiên cứu dự báo và đánh giá ảnh hưởng của khoảng tĩnh không đối với các công trình biển nổi có kể đến hiệu ứng phi tuyến bậc hai của tải trọng sóng

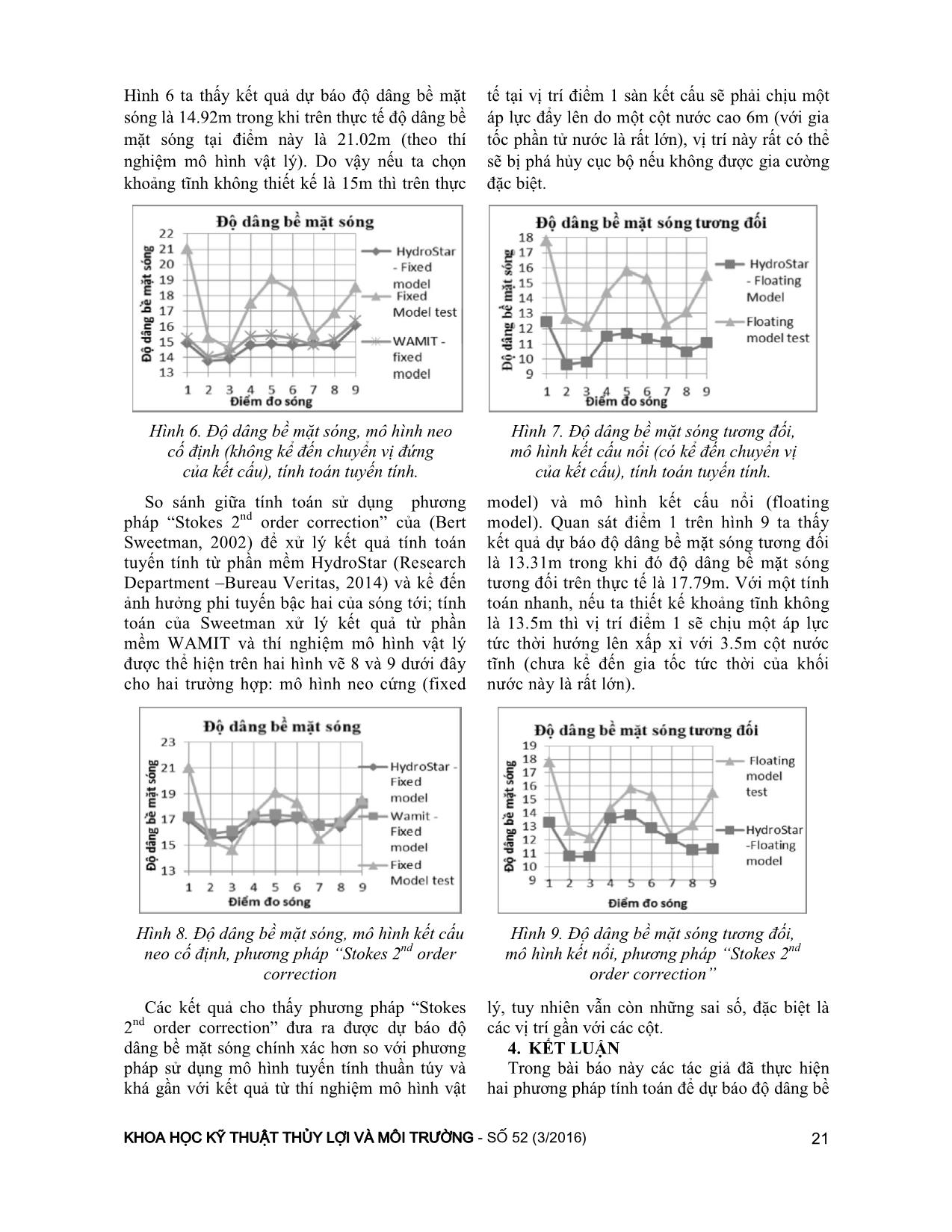
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016) 16 
BÀI BÁO KHOA HỌC 
NGHIÊN CỨU DỰ BÁO VÀ ĐÁNH GIÁ ẢNH HƯỞNG 
CỦA KHOẢNG TĨNH KHÔNG ĐỐI VỚI CÁC CÔNG TRÌNH BIỂN NỔI 
CÓ KỂ ĐẾN HIỆU ỨNG PHI TUYẾN BẬC HAI CỦA TẢI TRỌNG SÓNG 
Phạm Hiền Hậu1, Phạm Hồng Đức1 
Tóm tắt: Các phương pháp tính toán dự báo khoảng tĩnh không và ảnh hưởng của nó đối với các 
công trình biển nổi trong các tiêu chuẩn quy phạm hiện nay chủ yếu dựa vào các mô hình tuyến tính 
còn bộc lộ nhiều sai số và chưa cho những kết quả dự báo tin cậy. 
Trong bài báo này nhóm tác giả đã nghiên cứu dự báo và đánh giá ảnh hưởng của khoảng tĩnh 
không đối với các công trình biển nổi (Semi-submmersible, TLP,) bằng cách thực hiện tính toán 
tuyến tính trong miền tần số sử dụng phần mềm HydroStar (Research Department –Bureau Veritas, 
2014) và áp dụng phương pháp “Stokes 2nd order correction” đề xuất bởi (Bert Sweetman, 2002) là 
một phương pháp hiệu chỉnh kể đến ảnh hưởng của những hiệu ứng phi tuyến bậc hai. Mô hình 
Hermite đề xuất bởi (Winterstein, 1994) cũng được ứng dụng để xác định cực trị của các phản ứng 
phi tuyến bậc hai. 
Các kết quả tính toán đã được so sánh với tính toán của (Bert Sweetman, 2002) và thí nghiệm mô 
hình vật lý giàn Veslefrikk B thực hiện bởi MARINTEK Trondheim, Norway (1995). 
Từ khoá: Khoảng tĩnh không, độ dâng bề mặt sóng, HydroStar, WAMIT, Semi-submersible, TLP, 
hàm truyền bậc nhất, hàm truyền bậc hai, mô hình vật lý, mô hình Hermite. 
1. GIỚI THIỆU 
Trong  thiết  kế  các  công  trình  biển  nổi  như 
giàn  khoan  bán  chìm  (Semi-submersible),  giàn 
neo  đứng  (TLP),  việc  xác  định  khoảng  tĩnh 
không  là  hết  sức  phức  tạp  và  gây  nhiều  khó 
khăn cho người thiết kế vì đây là một giá trị rất 
nhạy cảm, ảnh hưởng trực tiếp đến ổn định, khả 
năng  mang  tải  và  các  yêu  cầu  chức  năng  của 
công trình. Cụ thể, một sự lựa chọn khoảng tĩnh 
không  nhỏ  có  thể  đặt  kết  cấu  nổi  trong  một 
trạng thái chịu tải trọng tác động của sóng biển 
lớn hơn,  làm  tăng  lực căng  trong hệ  thống dây 
neo, làm ngưng trệ hoạt động khoan... Mặt khác, 
một sự  lựa chọn khoảng  tĩnh không  lớn sẽ  làm 
tăng đáng kể giá thành kết cấu, giảm ổn định và 
khả  năng  mang  tải,  đồng  thời  ảnh  hưởng  đến 
những  yêu  cầu  khác  như  các  chuyển  vị  và  gia 
tốc của kết cấu. 
Hình 1. Shell Mars TLP trước và sau khi bị hư hại bởi bão Katrina (Photo: Wikipedia) 
Trước  thực  trạng nhiều1công  trình bị  hư hại 
1 Khoa Xây dựng Công trình biển & Dầu Khí, Trường 
Đại học Xây dựng. 
bởi  những  con  sóng  cực  hạn,  những  giải  pháp 
cho vấn đề về khoảng  tĩnh không  trở nên khẩn 
cấp  và  cần  thiết  hơn  bao  giờ  hết.  Giàn  Mars, 
một  giàn  khoan  và  khai  thác  dạng  neo  đứng 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016)  17
(TLP) (Hình 1) là một ví dụ. Hoạt động ở độ sâu 
896m ở khu vực vịnh Mexico, giàn Mars đã bị 
hư hại  lớn  trên sàn  thượng  tầng bởi những con 
sóng  bất  thường  trong  cơn  bão  Katrina.  Cùng 
với  giàn  Mars,  tổng  cộng  113  giàn  khác  đã  bị 
phá hủy hoặc hư hại nặng bởi những con  sóng 
trong  cơn  bão  Katrina  &  Rita.  Trong  các  quy 
trình thiết kế hiện hành, mô hình vật  lý thường 
là bắt buộc để đánh giá yêu cầu về khoảng tĩnh 
không cho các giàn Semi-submersible hoặc TLP 
xây  dựng  mới  trong  trường  hợp  không  có  dữ 
liệu  tham khảo  từ bất cứ một công  trình  tương 
tự nào  đã được xây dựng  trước đó. Tuy nhiên, 
việc thực hiện mô hình vật lý này là rất tốn kém 
và  chỉ  có  thể  được  thực  hiện  ở  giai  đoạn  cuối 
cùng của thiết kế. Chính vì vậy, một công cụ dự 
báo nhanh yêu cầu về khoảng tĩnh không là rất 
cần  thiết  trong  giai  đoạn  thiết  kế  cơ  sở,  góp 
phần  quan  trọng  làm  tăng  tính  cạnh  tranh  của 
thiết kế. Hơn nữa từ các kết quả dự báo đó, có 
thể  thiết kế gia cường cho kết cấu tại các vị  trí 
có  thể xuất hiện   khoảng tĩnh không  âm, tránh 
hư hại đến các kết cấu sàn thượng tầng. 
Các  phương  pháp  hiện  tại  để  mô  hình  hóa 
chuyển  vị  và  dự  báo  khoảng  tĩnh  không  cho 
giàn  bán  chìm  chủ  yếu  dựa  vào  các  phương 
pháp đơn giản hóa sử dụng các  tính toán nhiễu 
xạ và bức xạ bậc nhất cộng thêm một số dư dự 
trữ an toàn để kể đến tính không chính xác của 
phân  tích  tuyến  tính.  Phương  pháp  của  (Saeid 
Kazemi  và  Atilla  Incecik,  2005)  mang  tên 
“phương  pháp  phần  tử  biên  trực  tiếp  –  direct 
BEM” xem nguồn phi  tuyến chính nằm ở sóng 
tới,  trong khi các hiệu ứng nhiễu xạ và bức xạ 
bậc 2 được bỏ qua. Phương pháp này đã đưa ra 
một mô phỏng rất  tốt giá  trị khuếch đại của bề 
mặt  sóng  (nguyên  nhân  làm  giảm  khoảng  tĩnh 
không của công trình) trong trường hợp độ dốc 
của  sóng  tới  là  nhỏ,  khoảng  1/40.  Tuy  nhiên, 
trong những trạng thái biển khắc nghiệt (khi  độ 
dốc  của  sóng  rất  lớn)  phương  pháp  này  tỏ  ra 
không  chính  xác  và  thường  không  hữu  dụng 
trong dự báo khoảng tĩnh không và tác động củ ... 2. Các bước nghiên cứu để xác định 
khoảng tĩnh không đối với công trình biển nổi 
2.2. Cơ sở lý thuyết áp dụng trong dự báo 
khoảng tĩnh không của công trình biển nổi 
Giả thiết rằng kết cấu nổi dao động với biên 
độ  nhỏ  dưới  sự  tác  động  của  sóng  tới  là  sóng 
ngẫu nhiên (tập hợp của N con sóng đơn Airy) 
với  giả  thiết  độ  sâu  nước  vô  hạn  (bỏ  qua  ảnh 
hưởng của đáy). Trong lý thuyết nhiễu xạ tuyến 
tính, bài toán giá trị biên tổng quát có thể giả sử 
là tổ hợp tuyến tính của các bài toán sau: 
(i) Sóng  tới đập vào kết cấu nổi  (được  giữ 
đứng yên – bỏ qua các chuyển vị của kết cấu) sẽ 
bị nhiễu xạ do ảnh hưởng của sự có mặt của kết 
cấu. Bài toán này được gọi là bài toán nhiễu xạ. 
(ii) Kết  cấu  nổi  được  cho  dao  động  cưỡng 
bức  trong  môi  trường  nước  lặng    (không  có 
sóng  tới)  và  gây  ra  trường  sóng  bức  xạ  xung 
quanh  kết  cấu.  Bài  toán  này  được  gọi  là  bài 
toán bức xạ. 
Giả  sử  chất  lỏng nghiên cứu  là chất  lỏng  lý 
tưởng có chuyển động không xoáy, thế vận tốc 
tổng thể của dòng chất lỏng ở độ sâu nước vô 
hạn có thể viết dưới dạng hàm số phụ thuộc vào 
thời gian,  : 
 , , I D Rx y z         (2.1) 
Trong đó  I , D , R  tương ứng là hàm thế 
của sóng tới, sóng nhiễu xạ và bức xạ. 
Hình 3. Định nghĩa khoảng tĩnh không 
Khoảng  tĩnh  không  tức  thời  tại  một  điểm  - 
 t được  xác  định  bằng  khoảng  cách  giữa  vị 
trí của điểm đó tại đáy của sàn công tác so với 
độ  dâng  bề  mặt  sóng  cục  bộ  t   là  một  đại 
lượng ngẫu nhiên thay đổi theo thời gian.  
 0 0ver relt t t t       (2.2) 
0 - Khoảng  tĩnh không  trong điều kiện mặt 
nước tĩnh; 
 ver t - Chuyển vị theo phương đứng của sàn;                  
 er 3 4 5y sin sinv t x t     (2.3) 
 rel t - Độ dâng bề mặt sóng tương đối 
 rel vert t t         (2.4) 
Các  dạng  dao  động  của  một  công  trình  nổi 
bao gồm: 
- 1 , 2   , 3   :  tương ứng là 3 chuyển vị  tịnh 
tiến theo các phương x, y ,z; 
- 4 , 5 , 6 : 3 chuyển vị xoay quanh các trục 
x, y ,z. 
Độ dâng bề mặt sóng  t  với sự có mặt kết 
cấu nổi là tổng hợp của các thành phần sóng tới 
 I t ,  sóng  nhiễu  xạ  D t   và  sóng  bức  xạ 
 R t  theo phương trình (2.5): 
 I D Rt t t t                (2.5) 
Trong khi đó các thành phần sóng lại là tổng 
hợp của các thành phần bậc nhất và bậc hai: 
 1 2t t t                      (2.6) 
 1 1, 1, 1,I D Rt t t t            (2.7) 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016)  19
 2 2, 2, 2,I D Rt t t t          (2.8) 
Trong  các  tính  toán  sử dụng  mô  hình  tuyến 
tính chỉ các thành phần sóng bậc nhất được tính 
đến như trong phương trình (2.7). 
Đối với  tính  toán bậc  hai  đầy đủ,  tất  cả  các 
thành phần sóng bậc nhất và bậc hai được  tính 
đến như trong phương trình (2.6).  
Phương  pháp  “Stokes  2nd  ordre  correction” 
đề  xuất  bởi  (Bert  Sweetman,  2002)  là  một 
phương  pháp  lai  giữa  phương  pháp  tính  toán 
tuyến  tính  và  tính  toán  bậc  hai  đầy  đủ.  Ở  đây 
các  thành phần  sóng  tới,  sóng nhiễu xạ và bức 
xạ bậc nhất được  tính toán bằng phần mềm số, 
thành phần bậc hai của sóng tới sẽ được tính đến 
bằng  cách  sử  dụng hàm  truyền bậc  hai  theo  lý 
thuyết sóng Stokes, thành phần sóng nhiễu xạ và 
bức xạ bậc hai được bỏ qua. Khi đó độ dâng bề 
mặt sóng là tổng hợp của: 
 1, 1, 1, 2,I D R It t t t t      (2.9) 
 (1)1
1
Re k
n
i t
k k
k
t q A H e 
  ;  
 2, 2 2I t t t      (2.10) & (2.11) 
 ( )(2 )2
1 1
Re k l
n n
i t
k l kl
k l
t q A A H e   
   (2.12)  
 ( )(2 )2
1 1
Re k l
n n
i t
k l kl
k l
t q A A H e   
  (2.13) 
Trong đó:  
 1
kH   là  hàm  truyền  bậc  nhất  của  phản  ứng 
độ dâng bề mặt sóng xác định bằng phần mềm 
HydroStar  (Research  Department  –  Bureau 
Veritas, 2014). 
 2
klH
và 
 2
klH
  là hàm  truyền bậc hai  tần 
số  cao  và  tần  số  thấp  được  tính  toán  theo  lý 
thuyết Stokes bậc hai. 
Theo (Bernard Molin, 2002) với q=1/2: 
2 2
2 1
2
k l
klH
g
  ;
2 2
2 1
2
k l
klH
g
  
               (2.14) & (2.15) 
2.3. Xác định cực trị độ dâng bề mặt sóng 
a. Cực trị của phản ứng tuyến tính 
Kì vọng của cực trị (Mean maximum) của quá 
trình  chuẩn  (Gaussian  process)  u(t)  được  xác 
định theo (Bert Sweetman, 2002) bởi biểu thức: 
 max
0.577
2 ln
2 ln
E u N
N
         (2.16) 
Kì vọng của cực trị của phản ứng độ dâng bề 
mặt sóng (thành phần bậc nhất): 
 
11,max max
[ ]E E u                    (2.17) 
Trong  đó:  N:  số  chu  trình  trong  một  trạng 
thái biển  (3 – 6 giờ); 
1
 - Độ  lệch chuẩn của 
độ dâng bề mặt sóng (thành phần bậc nhất). 
b. Cực trị của phản ứng phi tuyến 
Cực trị của phản ứng phi tuyến bậc hai được 
xác  định  bằng  mô  hình  Hermite  đề  xuất  bởi 
(Winterstein,  1994).  Mô hình  Hermite  được  sử 
dụng để chuyển một quá trình ngẫu nhiên chuẩn 
(Gaussian)  bất  kì  thành  một  quá  trình  ngẫu 
nhiên  thực  tế  (phi  tuyến)  mà  chỉ  dựa  vào  4 
moment thống kê đầu tiên: giá trị trung bình, độ 
lệch chuẩn, độ bất đối xứng và độ nhọn. Nhóm 
tác  giả  đã  ứng  dụng  mô  hình  Hermite  và  lập 
trình trên chương trình Matlab để giải quyết bài 
toán xác định cực trị của phản ứng phi tuyến bậc 
hai (bổ sung vào tính toán tuyến tính bằng phần 
mềm  HydroStar).  Phản  ứng  phi  tuyến  (non-
Gaussian) ở đây là độ
dâng bề mặt sóng  t có 
quan  hệ  hàm  số  với  một  quá  trình  chuẩn 
(Gaussian process) u(t) như sau đây: 
2 3
3 4( ) [ ( 1) ( 3 )]H Hg u m k u c u c u u    (2.18) 
Trong đó:  m - giá trị trung bình;   - độ lệch 
chuẩn 
Trường  hợp  quá  trình  phi  tuyến  có  độ  lệch 
nhỏ so với quá trình chuẩn: 
3 3 / 6Hc ; 4 4( 3) / 24Hc  (2.19) & (2.20) 
Trường  hợp  quá  trình  phi  tuyến  có  độ  lệch 
lớn so với quá trình chuẩn: 
2
3 33
3
4
1 0.015 0.2
6 1 0.2( 3)
Hc
; 
0.8
41 0.12
3
4 40
4
1.43
1
3
Hc c
 (2.21) & (2.22) 
 
1/3
4
40
1 1.25( 3 1
10
c
; 
2 2
3 41 2 6H Hk c c              (2.23) & (2.24) 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016) 20 
3 -  độ  bất  đối  xứng  (skewness);  4 -  độ 
nhọn (kurtosis) 
Bốn  moment  thống  kê  này  được  tính  toán 
bằng cách giải bài toán trị riêng, vector riêng. 
Người ta đã chứng minh được rằng chỉ cần 4 
moment thống kê đầu tiên, không hơn là đủ để 
nắm  bắt  được  tính  chất  phi  tuyến  của  cực  trị 
(Winterstein,  1994).  Giả  thiết  rằng  sự  biến  đổi 
theo phương  trình (2.18)  là đúng với mọi điểm 
thời gian bao gồm cả điểm cực trị, ta có: 
 max max[ ] ( )E g E u             (2.25) 
3. SO SÁNH KẾT QUẢ TÍNH TOÁN 
VỚI THÍ NGHIỆM MÔ HÌNH VẬT LÝ 
3.1. Số liệu mô hình vật lý và mô hình hóa 
bằng HydroStar 
Mô hình được xây dựng với tỉ lệ 1:45 so với 
kích thước thực tế giàn bán chìm Veslefrikk B, 
mô hình được đặt trong bể thử
sóng tại Marintek 
với mô hình tạo sóng ngẫu nhiên. 
Hình 4. Mặt bằng và vị trí các ống đo sóng giàn 
bán chìm Veslefrikk B (Bert Sweetman, 2002) 
Hình 5. Mô hình HydroStar 
Bảng 1. Các thông số về giàn bán chìm 
Veslefrikk B (Bert Sweetman, 2002) 
Kích thước chi tiết giàn 
Chiều dài tổng thể (LOA)  107.5 m 
Khoảng cách các cột (dọc)  68 m 
Khoảng cách các cột (ngang)  67 m 
Chiều dài tiết diện cột  12.50 m 
Chiều rộng tiết diện cột  12.50 m 
Chiều rộng tiết pontoon  14.25 m 
Chiều cao pontoon  9.50 m 
Trạng thái làm việc của công trình 
Mớn nước, D  23 m 
Lượng chiếm nước  40692 T 
Khoảng  tĩnh  không  trong  điều 
kiện mặt nước tĩnh  17.50 m 
Trọng tâm quán tính   24.13 m 
Bán  kính  xoay  (lắc  ngang  - 
Pitch)  33.76 m 
Bán kính xoay (lắc dọc - Roll)  34.26 m 
Chiều cao khuynh tâm (GM)  2.36 m 
Độ sâu nước   175 m 
Bảng 2. Các thông số của phổ sóng áp dụng 
trong thí nghiệm (Bert Sweetman, 2002) 
Thông số phổ sóng 
Hs (m)  14 m 
Tp (s)  13.5 s 
Gamma  3 
Phổ sóng  JONSWAP 
Độ dốc của sóng  1./20 
3.2. So sánh các kết quả tính toán 
Kết  quả  so  sánh  giữa  tính  toán  tuyến  tính 
bằng phần mềm HydroStar, phần mềm WAMIT 
(tính  toán  của  Sweetman)  và  thí  nghiệm  mô 
hình vật lý được thể hiện trên hai hình vẽ 6 và 7 
dưới đây cho hai trường hợp mô hình: mô hình 
neo cứng (fixed model) – kết cấu được giữ đứng 
yên do đó không kể đến các chuyển vị của kết 
cấu  và  mô  hình  kết  cấu  nổi  (floating  model)  – 
có  kể  đến  các  chuyển  vị  của  kết  cấu.  So  sánh 
cho  thấy  tính  toán  tuyến  tính  bằng  hai  phần 
mềm  số  HydroStar  và  WAMIT  cho  kết  quả 
tương  tự  nhau  và  đều  cho  kết  quả  dự  báo  độ 
dâng  bề  mặt  sóng  nhỏ  hơn  đáng  kể  so  với  thí 
nghiệm  mô  hình  vật  lý.  Quan  sát  điểm  1  trên 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016)  21
Hình 6  ta  thấy kết quả dự báo độ dâng bề mặt 
sóng là 14.92m trong khi trên thực tế độ dâng bề 
mặt  sóng  tại  điểm  này  là  21.02m  (theo  thí 
nghiệm  mô  hình  vật  lý).  Do  vậy  nếu  ta  chọn 
khoảng tĩnh không thiết kế là 15m thì trên thực 
tế tại vị trí điểm 1 sàn kết cấu sẽ phải chịu một 
áp lực đẩy lên do một cột nước cao 6m (với gia 
tốc phần tử nước là rất lớn), vị trí này rất có thể 
sẽ bị phá hủy cục bộ nếu không được gia cường 
đặc biệt. 
Hình 6. Độ dâng bề mặt sóng, mô hình neo 
cố định (không kể đến chuyển vị đứng 
của kết cấu), tính toán tuyến tính. 
Hình 7. Độ dâng bề mặt sóng tương đối, 
mô hình kết cấu nổi (có kể đến chuyển vị 
của kết cấu), tính toán tuyến tính. 
So  sánh  giữa  tính  toán  sử  dụng    phương 
pháp  “Stokes  2nd  order  correction”  của  (Bert 
Sweetman,  2002)  để  xử  lý  kết  quả  tính  toán 
tuyến  tính  từ phần mềm HydroStar  (Research 
Department –Bureau Veritas, 2014) và kể đến 
ảnh hưởng phi tuyến bậc hai của sóng tới; tính 
toán  của  Sweetman  xử  lý  kết  quả  từ  phần 
mềm  WAMIT  và  thí  nghiệm  mô  hình  vật  lý 
được thể hiện trên hai hình vẽ 8 và 9 dưới đây 
cho hai  trường hợp: mô hình neo cứng  (fixed 
model)  và  mô  hình  kết  cấu  nổi  (floating 
model).  Quan  sát  điểm  1  trên  hình  9  ta  thấy 
kết quả dự báo độ dâng bề mặt sóng tương đối 
là  13.31m  trong  khi  đó  độ  dâng  bề  mặt  sóng 
tương đối trên thực tế là 17.79m. Với một tính 
toán nhanh, nếu ta thiết kế khoảng tĩnh không 
là  13.5m  thì  vị  trí  điểm 1  sẽ  chịu  một  áp  lực 
tức  thời  hướng  lên  xấp  xỉ  với  3.5m  cột  nước 
tĩnh  (chưa  kể  đến  gia  tốc  tức  thời  của  khối 
nước này là rất lớn). 
Hình 8. Độ dâng bề mặt sóng, mô hình kết cấu 
neo cố định, phương pháp “Stokes 2nd order 
correction 
Hình 9. Độ dâng bề mặt sóng tương đối, 
mô hình kết nổi, phương pháp “Stokes 2nd 
order correction” 
Các  kết  quả  cho  thấy  phương  pháp  “Stokes 
2nd  order  correction”  đưa  ra  được  dự  báo  độ 
dâng bề mặt sóng chính xác hơn so với phương 
pháp  sử dụng mô hình  tuyến  tính  thuần  túy và 
khá gần với kết quả  từ thí nghiệm mô hình vật 
lý,  tuy nhiên  vẫn còn những  sai  số,  đặc  biệt  là 
các vị trí gần với các cột. 
4. KẾT LUẬN 
Trong  bài  báo  này  các  tác  giả  đã  thực  hiện 
hai phương pháp tính toán để dự báo độ dâng bề 
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 52 (3/2016) 22 
mặt sóng và ảnh hưởng của khoảng tĩnh không 
đối  với  an  toàn  của  các  công  trình  biển  nổi: 
phương pháp tính toán bằng mô hình tuyến tính 
thuần  túy  bằng  sử  dụng  phần  mềm  HydroStar 
(Research  Department  –Bureau  Veritas,  2014) 
và  phương  pháp  “Stokes  2nd  order  correction” 
đề  xuất  bởi  Bert  Sweetman  (Bert  Sweetman, 
2002).  Mô  hình  Hermite  đề  xuất  bởi 
(Winterstein,  1994)  được  áp  dụng  để  xác  định 
cực trị của bài toán phi tuyến. Các kết quả một 
lần nữa khẳng định mô hình tính toán tuyến tính 
thuần  túy  là  chưa  phù hợp  đối  với  những  điều 
kiện biển khắc nghiệt khi tính chất phi tuyến của 
sóng là đáng kể (ở đây độ dốc của sóng là 5%). 
Kết quả tính toán theo phương pháp “Stokes 2nd 
order  correction”  của  Bert  Sweetman  cho  dự 
báo độ dâng bề mặt sóng tốt hơn tính toán tuyến 
tính  thuần  túy  và  khá  gần  với  thí  nghiệm  mô 
hình vật lý. Tuy nhiên phương pháp này vẫn còn 
một  số  hạn  chế:  chưa  kể  đến  ảnh  hưởng  phi 
tuyến của các thành phần sóng nhiễu xạ, bức xạ; 
chưa  kể  đến  ảnh  hưởng của  hiệu  ứng  sóng  leo 
tại các vị trí gần các cột; chưa kể đến ảnh hưởng 
phi  tuyến do độ cứng của hệ dây neo. Các hạn 
chế này sẽ được các  tác giả  tập trung làm sáng 
tỏ trong những nghiên cứu tiếp theo. 
TÀI LIỆU THAM KHẢO 
Research Department – Bureau Veritas, (2014), HydroStar manual. 
Bert  Sweetman,  Steven  R.  Winterstein  and  Trond  Stokka  Meling  (2002),  Air gap prediction from 
second-order diffraction and Stokes theory, Vol 12, No. 3, September 2002, Intl. Offshore Polar Eng. 
Bernard Molin, (2002), Hydrodynamic des structures offshore, Edition Technip. 
Bert Sweetman, (2001), Airgap analysis of floating structures subject to random seas: prediction of 
extremes using diffraction analysis versus model test results. 
Bert  Sweetman  (2002),  Practical airgap prediction for offshore structures,  Preprint  submitted  to 
Elsevier Science. 
Steven  R.  Winterstein,  Todd  C.  Ude,  and  Gudmund  Kleiven,  (1994),  Springing and slow-drift 
responses: predicted extremes and fatigue vs. simulation. 
Saeid Kazemi, Atilla Incecik (2005), Numerical prediction of air ap response of floating offshore 
structures using direct boundary element method, “Proceeding of 24th International Conference on 
Offshore Machanics and Arctic Engineering (OMAE2005). 
Abstract: 
ESTIMATION OF AIRGAP’S IMPACTS ON FLOATING STRUCTURES TAKING 
INTO ACCOUNT OF SECOND ORDER NON-LINEAR CORRECTIONS 
Actual standard methods of predicting airgap demands for floating structures in early design stages 
which are mostly based on linear models still yield uncertainties and lack required reliability. 
This paper presents a research on the prediction of airgap responses and its impacts on floating 
structures (Semi-submersible, TLP) based on the first order analysis in frequency domain using 
HydroStar (Research Department –Bureau Veritas, 2014). The “Stokes 2nd order correction” 
method proposed by (Bert Sweetman, 2002) is applied as a correction method to consider second-
order non-linear behaviors. The Hermite model of Steven R. (Winterstein, 1994) is also applied by 
programming in Matlab to determine the extreme values of second order responses (in addition to 
the conservative linear analysis by HydroStar software). 
All of the results are compared with Bert Sweetman’s results (Bert Sweetman, 2002) and the model 
test data of the Veslefrikk B Semi-submersible by MARINTEK Trondheim, Norway (1995). 
Keyword: Airgap, wave  elevations,  Semi-submersible,  TLP,  HydroStar,  WAMIT,  linear  transfer 
functions, quadratic transfer functions, model test, the Hermite model. 
BBT nhận bài: 26/11/2015 
Phản biện xong: 02/3/2016