Nghiên cứu đánh giá chất lượng và độ phức tạp một số thuật toán giải mã cho mã Polar

Kỹ thuật điện tử 
N. A. Hào, N. V. Phê, T. M. Hà, “ Nghiên cứu đánh giá chất lượng  cho mã POLAR.” 220 
NGHIÊN CỨU ĐÁNH GIÁ CHẤT LƯỢNG VÀ ĐỘ PHỨC TẠP 
MỘT SỐ THUẬT TOÁN GIẢI MÃ CHO MÃ POLAR 
Nguyễn Anh Hào1*, Nguyễn Văn Phê1, Trần Mạnh Hà2 
Tóm tắt: Bài báo phân tích giải pháp ứng dụng mã sửa lỗi Polar cho các hệ 
thống thông tin truyền dẫn số nói chung và định hướng phát triển ứng dụng cho hệ 
thống truyền dẫn số dung lượng cao hiện nay. Trong đó, phân tích và đánh giá chất 
lượng hai thuật toán giải mã, thuật toán gốc SC (Successive Calcelation Algorithm) 
và thuật toán mới SQ (Sequential Decoding Algorithm) trên kênh AWGN và điều 
chế là 4-QAM. Kết quả mô phỏng cho thấy, thuật toán giải mã SQ chất lượng tốt 
hơn đáng kể so với thuật toán SC, tuy nhiên phải trả giá bằng độ phức tạp tính toán. 
Từ khóa: Polar; SC; SQ; AWGN; QAM; FPGA. 
1. GIỚI THIỆU 
Năm 2016, Huawei công bố họ đã đạt được tốc độ là 27 Gbps trên các thiết bị 
5G nhờ ứng dụng mã Polar. Đây là một mốc quan trọng thể hiện khả năng ứng 
dụng mạnh mẽ của mã Polar trong việc giải quyết vấn đề tăng lưu lượng truyền 
thông cho các thiết bị thông tin hiện nay và cũng cho thấy cuộc chạy đua quyết liệt 
nhằm phát triển ứng dụng mã Polar cho các hệ thống truyền dẫn hiện đại. Rất 
nhiều các nghiên cứu gần đây cũng đã chứng minh rằng, mã Polar mang lại hiệu 
suất sử dụng phổ gấp 2-3 lần cho các hệ thống truyền dẫn. Về mặt mã hóa, mã 
Polar có thể tối ưu hóa lưu lượng kênh tiệm cận giới hạn Shannon. Đồng thời, nó 
cho phép giải mã với độ phức tạp tuyến tính, có nghĩa là độ trễ do xử lý ước lượng 
được. Phần còn lại của bài báo được bố cục như sau: Mục 2.1 giới thiệu tổng quan 
về mã Polar; Mục 2.2 và 2.3 phân tích 2 thuật toán giải mã SC và SQ cho mã 
Polar; Mục 2.4 đánh giá độ phức tạp; Mục 3 trình bày kết quả mô phỏng đánh giá 
chất lượng sửa lỗi 2 thuật toán trên cuối cùng là phần kết luận và đề xuất. 
2. NỘI DUNG 
 2.1. Tổng quan về mã Polar 
+
=
+
=
+
=
+
=
+
=
+
=
+
=
+
=
+
=
+
=
+
=
+
=
u0
u1
u2
u3
u4
u5
u6
u7
c0
c1
c2
c3
c4
c5
c6
c7
Hình 1. Lưới mã hóa, n = 8. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 221 
Mã Polar (n = 2
m
, k) là mã khối tuyến tính sinh bởi ma trận sinh 
m
mA F
 , với 
ma trận F là nhân biến đổi phân cực, ký hiệu m có nghĩa là m lần phép nhân ma 
trận Kronecker với chính nó. Nhân biến đổi phân cực là nhân Arikan 
1 0
1 1
F
. 
Như vậy, vecto mã cực 1
0
nc thu được là kết quả của phép phân ma trận 
1 1
0 0 ,
n n
mc u A
 với 10 0 1 1, ,...,
n
nu u u u
 , ui = 0, ,i với {0,1,..., 1}n là bộ 
n – k chỉ số của bit đóng băng. Các bit còn lại của vecto bit thông tin 1
0
nu được 
dùng để truyền dữ liệu. Quá trình mã hóa Polar được trình bày trên hình 1. 
2.2. Thuật toán giải mã loại trừ tuần tự cho mã Polar 
Để giải mã Polar, trong [1] tác giả đề xuất thuật toán loại trừ tuần tự SC 
(Successive Calcelation Algorithm). Thuật toán này thực hiện giải mã từng bit một 
cách tuần tự từ bit đầu tiên cho tới bit cuối cùng của mã khối, ngoài ra, quá trình 
giải mã mỗi bit sử dụng thông tin về tất cả các bit trước nó. Giả sử rằng, vector bit 
1
0
nu được truyền đi. Ở đầu thu, do bị nhiễu nên ta thu được tín hiệu 10
ny . Việc giải 
mã được thực hiện dựa trên đánh giá 
1 1
0 0,
1 1
0 0
: 0
arg max | :
n n
n n
u u
P u y
 
 1 10 0
0,1
arg max , | , 
0, ..
i
i n
i
u
i
P u u y i
u
i
 (1) 
Hình 2 mô tả quá trình tính toán giá trị tỉ lệ hợp lý LR (Likelihood Ratio) cho mỗi 
bit thu, một bước quan trọng trong thuật toán giải mã SC. Để giảm độ phức tạp tính 
toán, trong [2] đề xuất sử dụng logarit tỉ lệ hợp lý LLR (Log-Likelihood Ratio). 
Q
P
Q
P
Q
P
Q
P
Q
Q
P
P
Q
Q
P
P
Q
Q
Q
Q
P
P
P
P
y0
y1
y2
y3
y4
y5
y6
y7
Dec
Dec
Dec
Dec
Dec
Dec
Dec
Dec
0u
1u
2u
3u
4u
5u
6u
7u 
Hình 2. Lưới giải mã SC, n = 8. 
Như vậy, trong lưới giải mã sử dụng LLR dạng Ll,i, với l – Số cột trong lưới, 
 0,...,l m , i – Số hàng trong lưới, 0,..., 1i n . Khi đó, 10, 0 ,
n
iL y
 với 10
ny –
Vecto LLR đầu vào bộ giải mã, còn trên cơ sở ,m iL đưa ra quyết định về giá trị bit 
thứ i là iu . 
Kỹ thuật điện tử 
N. A. Hào, N. V. Phê, T. M. Hà, “ Nghiên cứu đánh giá chất lượng  cho mã POLAR.” 222 
Chúng ta định nghĩa pha giải mã  là tổng hợp các tính toán cần thiết để thu 
được mỗi giá trị mới , 0,..., 1 .u n  Khi đó, giá trị Ll,i được tính toán truy hồi 
và được cập nhật lại tại mỗi pha mới trong các khối. Các khối này được thể hiện 
trên hình 2 là khối P và Q. Dữ liệu đầu vào và đầu ra của các khối này được thể 
hiện trên hình 3. 
Q
P
PS
Ll-1,i-1
Ll-1,i
Ll,i
Ll-1,i
Ll-1,i+1
Ll,i
Hình 3. Các giá trị đầu vào và đầu ra của các khối P, Q. 
Các khối này tính toán các giá trị theo các công thức sau (trong trường hợp với LLR): 
 1, 1, 1 1, 1 1, 1, 1, sgn sgn , 1 max , ;l i l i l i l l i l iQ L L L L i L L (2) 
 1, 1, 1 1, 1, 1, , 1 ,S
P
S l i l i l i l iP P L L L L (3) 
với PS là giá trị tổng từng phần, được tính bằng cách cộng theo modulo 2 tất cả các 
bit đã được giải mã ở những pha trước. 
Quá trình giải mã bằng thuật toán SC có thể được biểu diễn dưới dạng cây như 
trong hình 4. Tại mỗi pha của quá trình giải mã, phụ thuộc vào quyết định cứng về 
giá trị bit đã được truyền đi mà lựa chọn một trong 2 nhánh. Xác định đường giải 
mã là một quá trình xác định các nhánh trên sơ đồ cây với số lượng bằng . 
0 1
0
0 0
0
0 0
1
1
1
11 1
Pha:
0
1
2
... ... ... ... ... ... ... ... 
Hình 4. Sơ đồ cây với các nhánh của thuật toán SC. 
Tiếp theo, ta sử dụng thuật ngữ “đường” tương đương với vector quyết định cứng 
của thuật toán giải mã. Trong hình 4, đường in đậm tương đương với vector 010. Rõ 
ràng là tại pha có bit đóng bằng thì không có sự phân nhánh trong sơ đồ cây. 
2.3. Thuật toán giải mã tuần tự với thứ tự ưu tiên SQ 
Trong [3] đề xuất thuật toán giải mã tuần tự sử dụng việc loại trừ một cách tuần 
tự với thứ tự ưu tiên SQ. Thông số cơ bản của thuật toán này là kích thước danh 
sách L (Khi L = 1 thuật toán này chính là thuật toán SC). 
Ý tưởng của thuật toán SQ dựa trên ý tưởng của thuật toán Successive 
Cancellation List Decoding – SCL) [4]. Thuật toán lưu L đường, mỗi đường có thể 
nối dài tiếp. Đồng thời thuật toán SQ tính xác suất các đường là lời giải của việc 
giải mã. Các đường với xác suất nhỏ nhất sẽ không được tiếp tục. Điều này dẫn 
đến giảm độ phức tạp của thuật toán trong khi khả năng kháng nhiễu hầu như 
không giảm. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 223 
Thuật toán giải mã SQ dùng một hàng ưu tiên PQ (Priority Queue) để lưu các 
đường cùng với các nhân (xác suất các đường là lời giải) tương ứng. Một PQ là 
một cấu trúc dữ liệu bao gồm các bộ dữ liệu (M, 1
0v
 ), với 1 1
0 0( , )
nM M v y là 
nhân của đường 1
0v
 , thuật toán xử lý cấu trúc dữ liệu bao gồm các bước sau [3]: 
1 - Đặt bộ dữ liệu vào ngăn xếp PQ; 
2 - Tách lấy một bộ dữ liệu (M, 1
0v
 ) với giá trị M lớn nhất; 
3 - Xóa một bộ dữ liệu với giá trị M nhỏ nhất khỏi ngăn xếp PQ. 
Ngoài ra, chúng ta đưa vào khái niệm bộ đếm số lần xử lý tại các pha 10
nt , số 
lần xử lý tại mỗi pha lớn nhất là D. Khi đó, thuật toán giải mã SQ cho mã phân cực 
có thể mô hình hóa như sau: 
1. Đặt vào PQ gốc của cây với nhân 0. Cho 10 0
nt ; 
2. Rút từ PQ bộ dữ liệu chứa 10v
 với giá trị của nhân lớn nhất. Cho 1t t  ; 
3. Nếu ,n trả về mã 10 ,
n
mv A
 thuật toán kết thúc; 
4. Nếu số bộ dữ liệu đang lưu trong ngăn xếp lớn hơn L, xóa từ ngăn xếp bộ dữ 
liệu với giá trị nhân nhỏ nhất; 
5. Tính toán các nhân 10 0, nM v y của các mã mở rộng có thể 0v sau đó đặt 
chúng vào ngăn xếp PQ; 
6. Nếu ,t D xóa từ PQ tất cả cá c bộ dữ liệu 
1
0 ,
jv j  ; 
7. Quay trở lại bước 2. 
Mỗi chu kỳ xử lý từ bước 2-7 chúng ta sẽ gọi là một lần lặp của thuật toán. Hàm 
nhân có thể có nhiều dạng, một trong số đó là biến thể của metric Fano như sau: 
1
1 1 1 1
0 0 , 0 0
0
, | , ,n i nm i i
i
M u y L u y u

   
  (5) 
 0, sgn 1
,
, otherwise
u
L
L u
L

 (6) 
với giá   – Hàm bù, giá trị của nó được tính toán trước. 
2.4. Phân tích độ phức tạp các thuật toán 
Thuật toán SC không đòi hỏi phải tính toán quá nhiều với độ phức tạp tính toán 
là O(nlogn). Nhưng thuật toán này có nhược điểm là nó không giải mã theo khả 
năng lớn nhất. Đồng thời thuật toán SC có độ trễ tính toán lớn do quá trình tính 
toán là tuần tự, và tăng theo chiều dài của mã. Trong khi đó, độ phức tạp của thuật 
toán SQ là O(Lnlogn). Đồng thời kết quả mô phỏng cho thấy rằng, khi tỉ lệ tín/tạp 
SNR lớn thì độ phức tạp của thuật toán SQ tiệm cận tới O(nlogn). Thuật toán SQ 
giải mã theo dấu hiệu khả năng lớn nhất nên khả năng kháng nhiễu tốt hơn hẳn so 
với thuật toán SC. 
Kỹ thuật điện tử 
N. A. Hào, N. V. Phê, T. M. Hà, “ Nghiên cứu đánh giá chất lượng  cho mã POLAR.” 224 
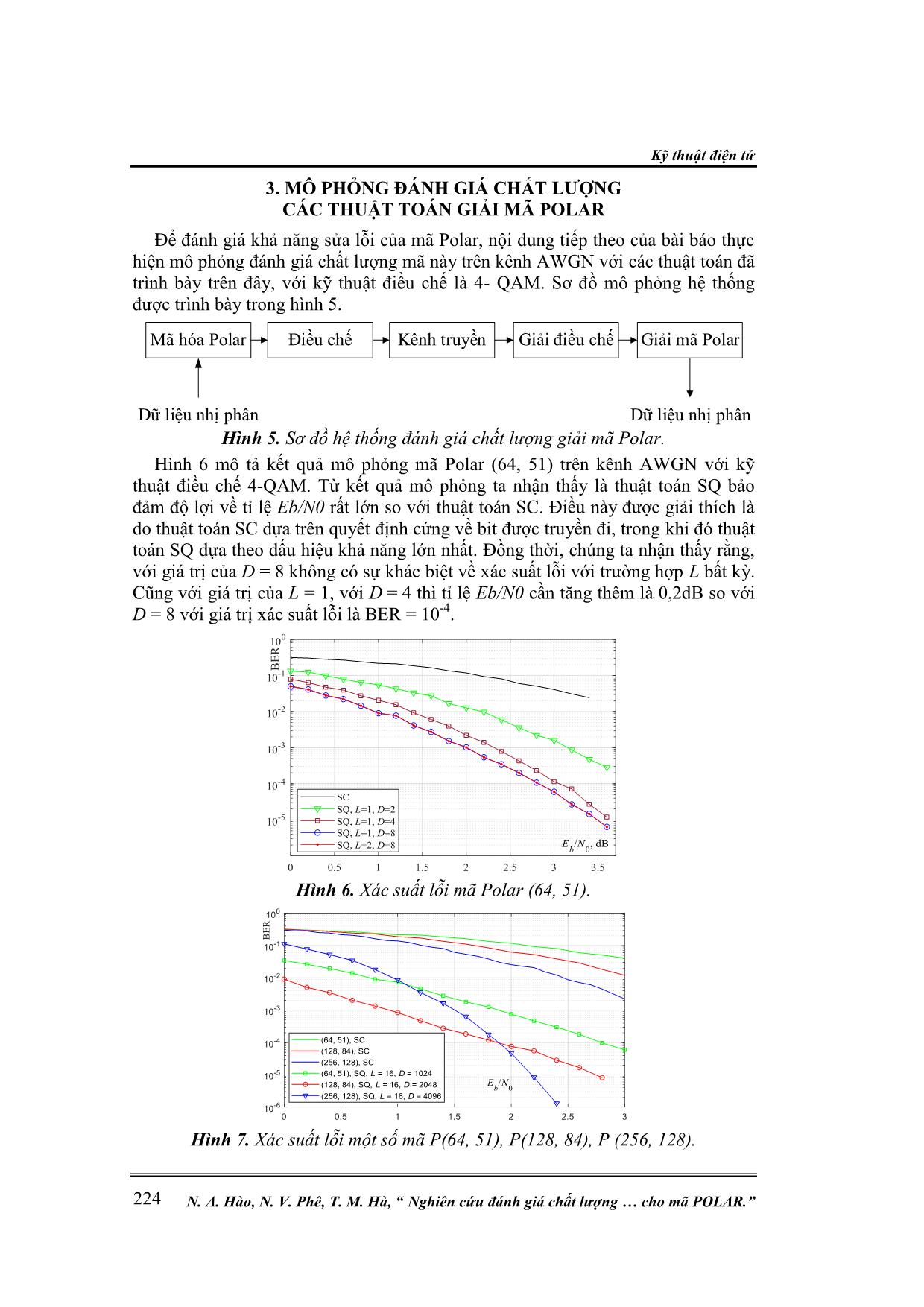
3. MÔ PHỎNG ĐÁNH GIÁ CHẤT LƯỢNG 
CÁC THUẬT TOÁN GIẢI MÃ POLAR 
Để đánh giá khả năng sửa lỗi của mã Polar, nội dung tiếp theo của bài báo thực 
hiện mô phỏng đánh giá chất lượng mã này trên kênh AWGN với các thuật toán đã 
trình bày trên đây, với kỹ thuật điều chế là 4- QAM. Sơ đồ mô phỏng hệ thống 
được trình bày trong hình 5. 
Mã hóa Polar Điều chế Kênh truyền Giải điều chế Giải mã Polar
Dữ liệu nhị phân Dữ liệu nhị phân
Hình 5. Sơ đồ hệ thống đánh giá chất lượng giải mã Polar. 
Hình 6 mô tả kết quả mô phỏng mã Polar (64, 51) trên kênh AWGN với kỹ 
thuật điều chế 4-QAM. Từ kết quả mô phỏng ta nhận thấy là thuật toán SQ bảo 
đảm độ lợi về tỉ lệ Eb/N0 rất lớn so với thuật toán SC. Điều này được giải thích là 
do thuật toán SC dựa trên quyết định cứng về bit được truyền đi, trong khi đó thuật 
toán SQ dựa theo dấu hiệu khả năng lớn nhất. Đồng thời, chúng ta nhận thấy rằng, 
với giá trị của D = 8 không có sự khác biệt về xác suất lỗi với trường hợp L bất kỳ. 
Cũng với giá trị của L = 1, với D = 4 thì tỉ lệ Eb/N0 cần tăng thêm là 0,2dB so với 
D = 8 với giá trị xác suất lỗi là BER = 10-4. 
Hình 6. Xác suất lỗi mã Polar (64, 51). 
Hình 7. Xác suất lỗi một số mã P(64, 51), P(128, 84), P (256, 128). 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 225 
Hình 7 biểu thị so sánh xác suất lỗi của các mã phân cực (64, 51); (128, 84); 
(256, 128) với L = 32 và D = Ln. Với các ứng dụng trên thực tế, độ phức tạp của 
thuật toán chỉ phụ thuộc vào chiều dài mã khối n và số lần xử lý tại mỗi pha L. Kích 
thức ngăn xếp D thực tế chỉ là kích thước của bộ nhớ. Từ kết quả mô phỏng ta nhận 
thấy với L = 32 thì xu hướng giảm về tỉ lệ tín hiệu/nhiễu tiếp tục được duy trì. 
4. KẾT LUẬN VÀ ĐỀ XUẤT 
Một nghiên cứu trước đây đã sử dụng mã Polar để mã hóa khung dữ liệu MELP 
đã mang lại độ lợi mã hóa đến 0,8 dB ở vùng Eb/N0 cao (khoảng 7dB) so với mã 
Hamming (7,4), với độ phức tạp chấp nhận được [5]. Kết quả lần này càng khẳng 
định lợi ích tăng hiệu suất phổ một cách rõ ràng của mã Polar. 
Thuật toán SC cân bằng giữa độ phức tạp và hiệu suất sửa lỗi, có thể phát triển 
ứng dụng cho các hệ thống truyền dẫn lưu lượng nhỏ và vừa. Đặc biệt là ứng dụng 
cho hệ thống truyền dẫn số có yêu cầu kháng nhiễu thấp. Thuật toán SQ có độ 
phức tạp tính toán cao, có nhớ nhưng hiệu suất và khả năng kháng nhiễu vượt trội 
hơn hẳn. Vì vậy, hoàn toàn có thể phát triển ứng dụng cho các hệ thống đường trục 
chính như viba số, VISAT, hoặc các hệ thống thông tin di động 4G, 5G. 
Về độ phức tạp của thuật toán là O(Lnlogn) so với O(nlogn) của SC, nếu có thể 
giải quyết bằng xây dựng kiến trúc xử lý song song L kênh dựa trên giải pháp 
FPGA thì độ phức tạp tính toán về lý thuyết chỉ ngang bằng với giải thuật SC. 
Thuật toán SCL (Successive Calcelation List Algorithm) nêu ra ở [4] và là cơ sở 
cho thuật toán SQ đã được thực hiện trên cơ sở giải pháp FPGA ở [6]. Tại đây, độ 
trễ xử lý ước lượng được là: 
Bảng 1. Độ trễ (Latency) cho N=1024, P=14 và L=4. 
 LPU 
LL Precision List Size LUTs Latency (ns) 
8 
2 144 3.52 
4 360 3.98 
8 976 4.16 
16 2976 4.30 
32 12096 4.76 
16 
2 312 3.66 
4 760 4.11 
8 2032 4.30 
16 6112 4.46 
32 24512 4.91 
Như vậy, với việc thiết kế phần mềm và xây dựng phần cứng hệ thống trên cơ 
sở công nghệ FPGA, phối hợp DSP (Digital signal processor) để kiến trúc xử lý 
song song và tối ưu bộ mã hóa và giải mã bằng công nghệ trí tuệ nhân tạo (AI 
Tech), độ trễ của SQ có thể còn thấp hơn nhiều lần so với kết quả trên. Đồng thời, 
hướng phát triển này sẽ cải thiện tối đa hiệu suất mã và đưa lưu lượng tiệm cận đến 
lưu lượng kênh truyền dẫn theo lý thuyết Shannon. 
Kỹ thuật điện tử 
N. A. Hào, N. V. Phê, T. M. Hà, “ Nghiên cứu đánh giá chất lượng  cho mã POLAR.” 226 
TÀI LIỆU THAM KHẢO 
[1]. E. Arikan, “Channel polarization: A method for constructing capacity 
achieving codes for symmetric binary-input memoryless channels,” IEEE 
Transactions on Information Theory, vol. 55, no. 7, pp. 3051–3073, July 2009. 
[2]. C. Leroux, A. J. Raymond, G. Sarkis, and W. J. Gross, “A semi-parallel 
successive-cancellation decoder for polar codes,” IEEE Trans. Signal 
Process., vol. 61, no. 2, pp. 289–299, Jan. 2013. 
[3]. V. Miloslavkaya, P. Trifonov, “Sequential Decoding of Polar Codes,” IEEE 
Communications Letters, vol. 18, no. 2, july 2014. 
[4]. Tal and A. Vardy, “List decoding of polar codes,” IEEE Transactions On 
Information Theory, vol. 61, no. 5, pp. 2213–2226, May 2015. 
[5]. Nguyễn Anh Hào và Phạm Xuân Nghĩa, “Ứng dụng mã cực (Polar) trong mã 
hóa tiếng nói tốc độ thấp theo chuẩn MELP”, REV- ECIT 2018. 
[6]. Altug Sural, “An FPGA implementation of successive cancellation list 
decoding for polar codes”, January 2016. 
ABSTRACT 
THE EVALUATION OF PERFORMANCE AND COMPUTATIONAL 
COMPLEXITY OF DECODING ALGORITHMS FOR POLAR CODE 
In this paper, the application of the Polar code for digital communication 
systems in general is analysed and its potential application for the high-
capacity modern digital communication systems in particular is suggested. 
In this paper, two algorithms: the original Successive Cancelation Algorithm 
and the developed Sequential Decoding Algorithm are analysed and 
evaluated on AWGN channel and 4-QAM signal. The simulation results show 
that the AQ decoding algorithm performs better than the SC algorithm, but 
the performance comes with high computational complexity. 
Keywords: Polar; SC; SQ; AWGN; QAM; FPGA. 
Nhận bài ngày 18 tháng 3 năm 2020 
Hoàn thiện ngày 20 tháng 8 năm 2020 
Chấp nhận đăng ngày 28 tháng 8 năm 2020 
Địa chỉ: 1Trung tâm Kỹ thuật thông tin công nghệ cao; 
2
Viện Điện tử, số 17 Hoàng Sâm, Nghĩa Đô, Cầu Giấy, Hà Nội. 
*Email: hao6379@gmail.com.