Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet
Tóm tắt: Thông tin trực quan được truyền tải dưới dạng hình ảnh kỹ thuật số đang trở
thành một phương thức truyền thông chính, tuy nhiên, các hình ảnh trong quá trình nhận,
mã hóa và truyền đi thường bị hỏng hoặc rung mờ do nhiễu và phương pháp chụp ảnh. Để
cải thiện chất lượng hình ảnh, một số kỹ thuật đã được đề xuất như biến đổi Wavelet rời
rạc, biến đổi Wavelet phức cây kép, các bộ lọc truyền thống,. Tuy nhiên, vẫn chưa thể
đem lại hiệu quả cao do vẫn tồn tại nhiễu cao, cho kết quả hình ảnh không tốt, chưa tối ưu
về độ phức tạp tính toán, mức tiêu thụ bộ nhớ và tốc độ xử lý. Trong khuôn khổ nội dung
bài báo này, chúng tôi đề xuất sử dụng phương pháp dựa trên biến đổi Curvelet để nâng
cao chất lượng ảnh.
Từ khóa: Biến đổi Curvelet; Khử nhiễu ảnh; Biến đổi Wavelet cây kép phức.
1. MỞ ĐẦU
Hình ảnh thường có nhiễu và nó không dễ dàng loại bỏ trong quá trình xử lý hình ảnh. Theo
đặc trưng ảnh thực tế, tính chất thống kê nhiễu và quy luật phân bố phổ tần số, người ta đã phát
triển nhiều phương pháp khử nhiễu, chúng được chia tương đối thành trường không gian và
trường biến đổi như phương pháp trung bình vùng lân cận, biến đổi Wavelet,. Các phương pháp
này nhìn chung có một vấn đề nan giải, đó là độ mịn nhiễu, lưu giữ thông tin chi tiết và rìa ảnh.
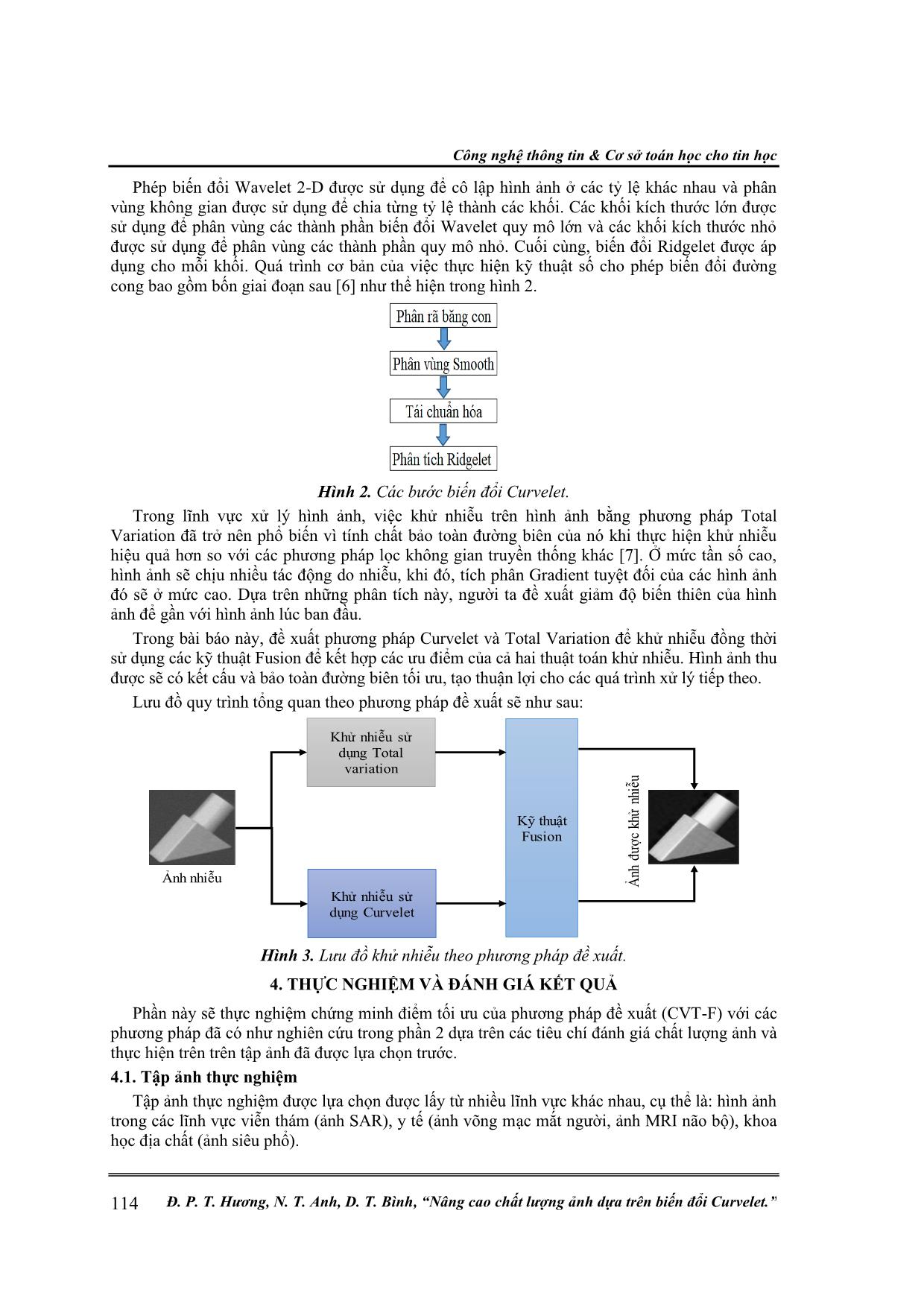
Trong những năm gần đây, một loại biến đổi đa cấp mới dựa trên biến đổi Wavelet - biến đổi
Curvelet đã phát triển nhanh chóng (E.J.Candes, 1999). Các yếu tố cấu trúc của phép biến đổi
Curvelet bao gồm các tham số về kích thước, vị trí và nhiều hơn nữa là tham số định hướng cho
phép nó có đặc tính định hướng tốt. Theo đó, phép biến đổi Curvelet ưu việt hơn Wavelet cũng
như một số phương pháp truyền thống khác trong việc biểu thị đường biên hình ảnh, chẳng hạn
như đặc trưng hình học của đường cong và đường bao, đã thu được kết quả nghiên cứu tốt trong
việc xử lý hình ảnh. Bài báo này đưa ra một phương pháp cải tiến dựa trên phép biến đổi
Curvelet sử dụng kỹ thuật Fusion để hợp nhất ảnh xử lý với phương pháp biến phân toàn phần
(Total Variation) [7].

Trang 1

Trang 2
Trang 3

Trang 4
Trang 5
Trang 6

Trang 7
Tóm tắt nội dung tài liệu: Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet

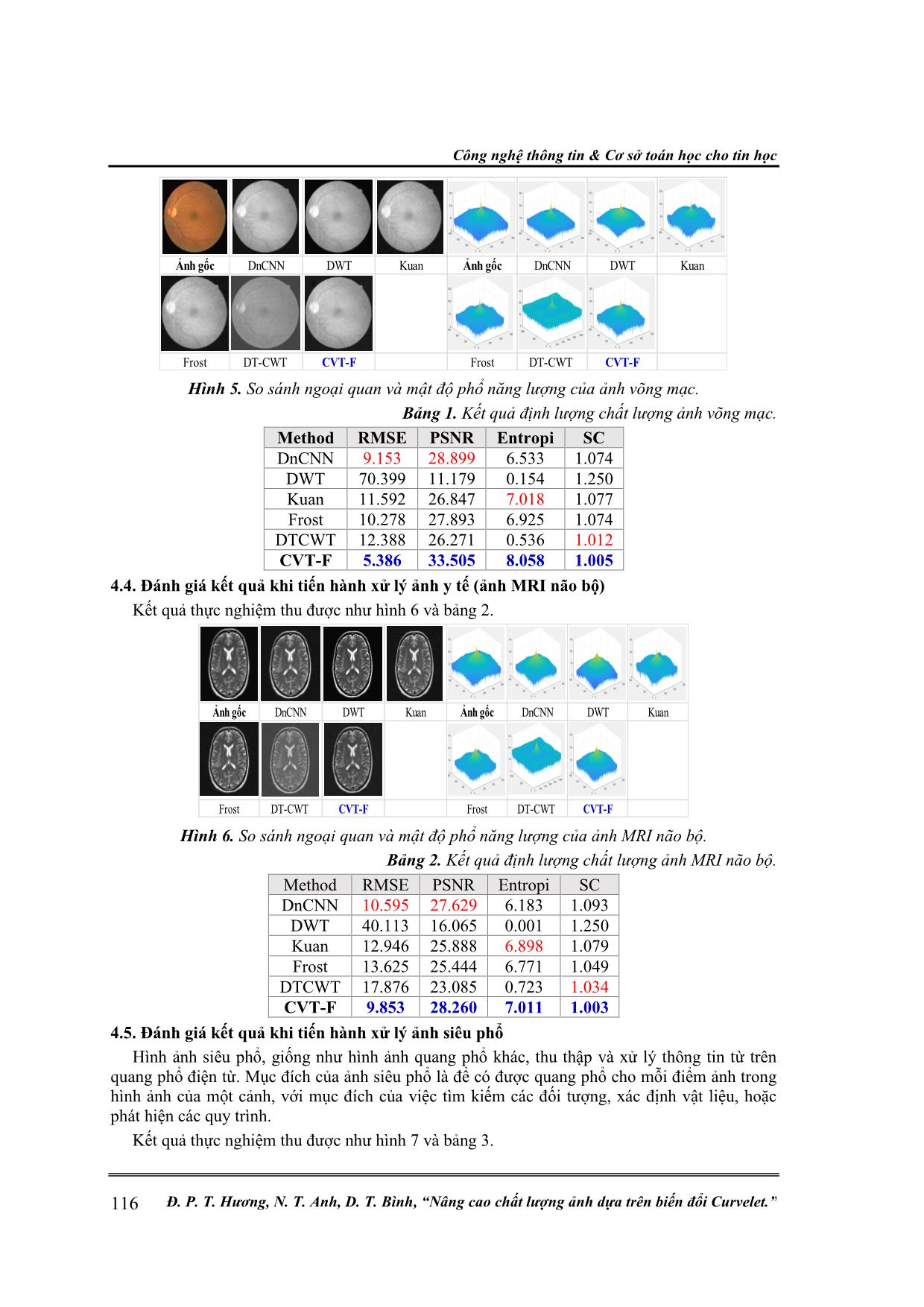
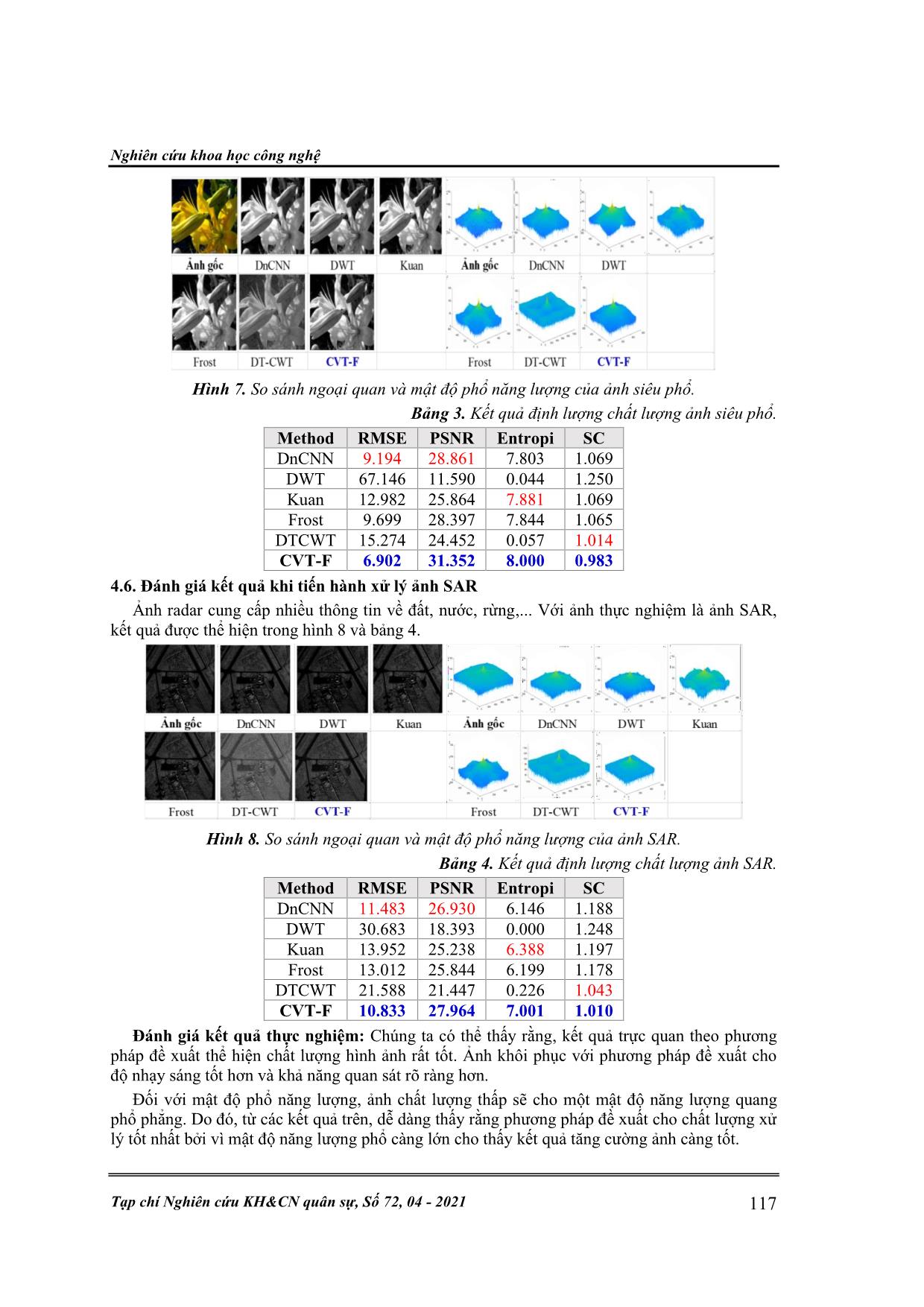
Công nghệ thông tin & Cơ sở toán học cho tin học 112 Đ. P. T. Hương, N. T. Anh, D. T. Bình, “Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet.” NÂNG CAO CHẤT LƯỢNG ẢNH DỰA TRÊN BIẾN ĐỔI CURVELET Đặng Phan Thu Hương1, Nguyễn Thúy Anh2, Doãn Thanh Bình3* Tóm tắt: Thông tin trực quan được truyền tải dưới dạng hình ảnh kỹ thuật số đang trở thành một phương thức truyền thông chính, tuy nhiên, các hình ảnh trong quá trình nhận, mã hóa và truyền đi thường bị hỏng hoặc rung mờ do nhiễu và phương pháp chụp ảnh. Để cải thiện chất lượng hình ảnh, một số kỹ thuật đã được đề xuất như biến đổi Wavelet rời rạc, biến đổi Wavelet phức cây kép, các bộ lọc truyền thống,... Tuy nhiên, vẫn chưa thể đem lại hiệu quả cao do vẫn tồn tại nhiễu cao, cho kết quả hình ảnh không tốt, chưa tối ưu về độ phức tạp tính toán, mức tiêu thụ bộ nhớ và tốc độ xử lý. Trong khuôn khổ nội dung bài báo này, chúng tôi đề xuất sử dụng phương pháp dựa trên biến đổi Curvelet để nâng cao chất lượng ảnh. Từ khóa: Biến đổi Curvelet; Khử nhiễu ảnh; Biến đổi Wavelet cây kép phức. 1. MỞ ĐẦU Hình ảnh thường có nhiễu và nó không dễ dàng loại bỏ trong quá trình xử lý hình ảnh. Theo đặc trưng ảnh thực tế, tính chất thống kê nhiễu và quy luật phân bố phổ tần số, người ta đã phát triển nhiều phương pháp khử nhiễu, chúng được chia tương đối thành trường không gian và trường biến đổi như phương pháp trung bình vùng lân cận, biến đổi Wavelet,... Các phương pháp này nhìn chung có một vấn đề nan giải, đó là độ mịn nhiễu, lưu giữ thông tin chi tiết và rìa ảnh. Trong những năm gần đây, một loại biến đổi đa cấp mới dựa trên biến đổi Wavelet - biến đổi Curvelet đã phát triển nhanh chóng (E.J.Candes, 1999). Các yếu tố cấu trúc của phép biến đổi Curvelet bao gồm các tham số về kích thước, vị trí và nhiều hơn nữa là tham số định hướng cho phép nó có đặc tính định hướng tốt. Theo đó, phép biến đổi Curvelet ưu việt hơn Wavelet cũng như một số phương pháp truyền thống khác trong việc biểu thị đường biên hình ảnh, chẳng hạn như đặc trưng hình học của đường cong và đường bao, đã thu được kết quả nghiên cứu tốt trong việc xử lý hình ảnh. Bài báo này đưa ra một phương pháp cải tiến dựa trên phép biến đổi Curvelet sử dụng kỹ thuật Fusion để hợp nhất ảnh xử lý với phương pháp biến phân toàn phần (Total Variation) [7]. 2. CÁC NGHIÊN CỨU LIÊN QUAN Trong thực tế, đã có một số giải pháp nhằm nâng cao chất lượng ảnh được nghiên cứu và áp dụng như: Biến đổi Wavelet rời rạc (DWT- Discrete Wavelet Transform), Biến đổi Wavelet phức hợp cây kép (DTCWT), sử dụng mạng nơ ron được huấn luyện (DnCNN), sử dụng bộ lọc Kuan và phương pháp sử dụng bộ lọc Frost. 2.1. Phương pháp dựa vào biến đổi Wavelet rời rạc (DWT) Biến đổi Wavelet có thuộc tính đa tỷ lệ, cục bộ hóa tần số thời gian tốt. Do đó, kỹ thuật bộ lọc dựa trên Wavelet được sử dụng rộng rãi trong việc giảm nhiễu hình ảnh. Tuy nhiên, hiệu quả của các Wavelet hai chiều (2-D) tiêu chuẩn bị giới hạn bởi tính đẳng hướng trong không gian và thiếu tính bất biến dịch chuyển của các hàm cơ sở của chúng [1]. 2.2. Phương pháp dựa vào biến đổi Wavelet phức hợp cây kép (DTCWT) Đối với phương pháp dựa trên biến đổi Wavelet rời rạc, chỉ với một sự thay đổi nhỏ trong tín hiệu đầu vào có thể gây ra các hệ số Wavelet đầu ra rất khác nhau. Đây là hạn chế chính của Wavelet trong nhận dạng mẫu. Một cách để khắc phục điều này là thực hiện phép biến đổi Wavelet mà không có số thập phân. Hạn chế của phương pháp này là nó không hiệu quả về mặt tính toán, đặc biệt là trong nhiều chiều. Kingsbury đã giới thiệu một loại biến đổi Wavelet mới, được gọi là biến đổi Wavelet phức hợp cây kép, thể hiện tính chất bất biến dịch chuyển gần đúng Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 113 và độ phân giải gốc được cải thiện. Sự thành công của phép biến đổi là do việc sử dụng các bộ lọc trong không gian (a,b). Ông đề xuất một độ trễ đơn giản của một mẫu giữa các bộ lọc cấp 1 trong mỗi không gian, sau đó, sử dụng các bộ lọc pha tuyến tính độ dài chẵn và lẻ thay thế [2]. 2.3. Phương pháp mạng nơ ron được huấn luyện (DnCNN) Một phương pháp được sử dụng để loại bỏ nhiễu là sử dụng mạng DnCNN được huấn luyện nhằm loại bỏ nhiễu Gaussian. Loại bỏ nhiễu với mạng được huấn luyện có những hạn chế sau [3]: - Loại bỏ nhiễu chỉ hoạt động với hình ảnh đơn kênh 2-D; - Mạng chỉ nhận dạng nhiễu Gaussian, với một phạm vi độ lệch chuẩn hạn chế. Hình 1. Quy trình khử nhiễu DnCNN. 2.4. Phương pháp sử dụng bộ lọc Kuan [5] Kuan thực hiện lọc không gian trên từng pixel riêng lẻ bằng cách sử dụng các giá trị mức xám trong một cửa sổ hình vuông bao quanh mỗi pixel. Kích thước của bộ lọc phải là số lẻ và có thể từ 3x3 đến 11x11 pixel. Tất cả các pixel đều được lọc. Để lọc các pixel nằm gần các đường biên của hình ảnh, các pixel đường biên được sao chép để cung cấp đủ dữ liệu. Giá trị cấp xám R thu được cho pixel được làm mịn là: R = CP * W + I * (1-W) Trong đó, Cu = 1/NLOOK, Ci = VAR/I, W = (1-Cu / Ci)/(1 + Cu), I = Mức xám trung bình trong cửa sổ bộ lọc, CP = pixel trung tâm trong cửa sổ bộ lọc, VAR = Phương sai trong cửa sổ bộ lọc, NLOOK = Số lần hiển thị. 2.5. Phương pháp sử dụng bộ lọc Frost [4] Nguyên lý hoạt động của bộ lọc này là xác định bộ lọc đối xứng tròn với tập hợp các giá trị trọng số M cho mỗi pixel: M = exp (- A * T) Trong đó, A = DAMP * (V/I2), T là giá trị tuyệt đối của khoảng cách pixel từ pixel trung tâm đến các điểm lân cận của nó trong cửa sổ bộ lọc, DAMP là hệ số làm giảm hàm mũ, V là phương sai của mức xám trong cửa sổ bộ lọc, I2 là bình phương của mức xám trung bình trong cửa sổ bộ lọc, giá trị cấp xám R thu được cho pixel được làm mịn là: R = (P1 * M1 + P2 * M2 + ... + Pn * Mn)/(M1 + M2 + ... + Mn) Trong đó, P1, ..., Pn là mức xám của mỗi pixel trong cửa sổ bộ lọc và M1, ..., Mn là trọng số cho mỗi pixel. 3. PHƯƠNG PHÁP ĐỀ XUẤT DỰA TRÊN BIẾN ĐỔI CURVELET (CVT-F) Dựa trên nghiên cứu các phương ở phần 2, nhóm tác giả đã tiến hành xây dựng phương pháp nâng cao chất lượng hình ảnh dựa trên phép biến đổi Curvelet. Cụ thể: Công nghệ thông tin & Cơ sở toán học cho tin học 114 Đ. P. T. Hương, N. T. Anh, D. T. Bình, “Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet.” Phép biến đổi Wavelet 2-D được sử dụng để cô lập hình ảnh ở các tỷ lệ khác nhau và phân vùng không gian được sử dụng để chia từng tỷ lệ thành các khối. Các khối kích thước lớn được sử dụng để phân vùng các thành phần biến đổi Wavelet quy mô lớn và các khối kích thước nhỏ được sử dụng để phân vùng các thành phần quy mô nhỏ. Cuối cùng, biến đổi Ridgelet được áp dụng cho mỗi khối. Quá trình cơ bản của việc thực hiện kỹ thuật số cho phép biến đổi đường cong bao gồm bốn giai đoạn sau [6] như thể hiện trong hình 2. Hình 2. Các bước biến đổi Curvelet. Trong lĩnh vực xử lý hình ảnh, việc khử nhiễu trên hình ảnh bằng phương pháp Total Variation đã trở nên phổ biến vì tính chất bảo toàn đường biên của nó khi thực hiện khử nhiễu hiệu quả hơn so với các phương pháp lọc không gian truyền thống khác [7]. Ở mức tần số cao, hình ảnh sẽ chịu nhiều tác động do nhiễu, khi đó, tích phân Gradient tuyệt đối của các hình ảnh đó sẽ ở mức cao. Dựa trên những phân tích này, người ta đề xuất giảm độ biến thiên của hình ảnh để gần với hình ảnh lúc ban đầu. Trong bài báo này, đề xuất phương pháp Curvelet và Total Variation để khử nhiễu đồng thời sử dụng các kỹ thuật Fusion để kết hợp các ưu điểm của cả hai thuật toán khử nhiễu. Hình ảnh thu được sẽ có kết cấu và bảo toàn đường biên tối ưu, tạo thuận lợi cho các quá trình xử lý tiếp theo. Lưu đồ quy trình tổng quan theo phương pháp đề xuất sẽ như sau: Hình 3. Lưu đồ khử nhiễu theo phương pháp đề xuất. 4. THỰC NGHIỆM VÀ ĐÁNH GIÁ KẾT QUẢ Phần này sẽ thực nghiệm chứng minh điểm tối ưu của phương pháp đề xuất (CVT-F) với các phương pháp đã có như nghiên cứu trong phần 2 dựa trên các tiêu chí đánh giá chất lượng ảnh và thực hiện trên trên tập ảnh đã được lựa chọn trước. 4.1. Tập ảnh thực nghiệm Tập ảnh thực nghiệm được lựa chọn được lấy từ nhiều lĩnh vực khác nhau, cụ thể là: hình ảnh trong các lĩnh vực viễn thám (ảnh SAR), y tế (ảnh võng mạc mắt người, ảnh MRI não bộ), khoa học địa chất (ảnh siêu phổ). Ảnh nhiễu Khử nhiễu sử dụng Total variation Khử nhiễu sử dụng Curvelet Kỹ thuật Fusion Ả nh đư ợ c kh ử n hi ễu Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 115 Hình 4. Tập ảnh thực nghiệm. 4.2. Các thông số đánh giá chất lượng hình ảnh Trong khuôn khổ nội dung bài báo, các tham số được sử dụng để đánh giá chất lượng hình ảnh là: Entropi, sai số toàn phương trung bình RMSE, tỷ số tín hiệu cực đại trên nhiễu PSNR, đánh giá cấu trúc ảnh SC (Structural Content). Entropi được tính toán theo công thức: Trong đó, k là số lượng các mức xám và pk là xác suất được kết hợp với mức xám k. Thông số RMSE được tính toán: Trong đó, i và j biểu thị vị trí không gian của pixel. M và N là kích thước của ảnh. Tỷ số tín hiệu trên nhiễu cực đại PSNR được tính toán theo công thức: Trong đó, I(i,j) là ảnh gốc, F(i,j) là ảnh hợp nhất (Fused Image) và MxN là kích thước ảnh I. Thông số đánh giá cấu trúc ảnh SC, được tính toán: Trong đó, f(i,j) là ảnh gốc, f’(i,j) là ảnh hợp nhất (fused image) và MxN là kích thước ảnh f. 4.3. Đánh giá kết quả khi tiến hành xử lý ảnh y tế (ảnh võng mạc) Tiến hành thực nghiệm, ta thu được kết quả hình ảnh trực quan, mật độ phổ năng lượng của ảnh võng mạc (như hình 5) và các thông số đánh giá chất lượng hình ảnh khi sử dụng các phương pháp đã nghiên cứu với phương pháp đề xuất (như bảng 1). log( )k k k H p p= − 2 ( , ) ( , )R i j F i j RMSE MN − = ( ) 2 10 2 1 10l g n PSNR o MSE − = 2 1 1 ( , ) ( , )M N i j I i j F i j MSE M N= = − = 2 1 1 2 ' 1 1 ( , ) ( , ) M N i j M N i j f i j SC f i j = = = = = Công nghệ thông tin & Cơ sở toán học cho tin học 116 Đ. P. T. Hương, N. T. Anh, D. T. Bình, “Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet.” Hình 5. So sánh ngoại quan và mật độ phổ năng lượng của ảnh võng mạc. Bảng 1. Kết quả định lượng chất lượng ảnh võng mạc. Method RMSE PSNR Entropi SC DnCNN 9.153 28.899 6.533 1.074 DWT 70.399 11.179 0.154 1.250 Kuan 11.592 26.847 7.018 1.077 Frost 10.278 27.893 6.925 1.074 DTCWT 12.388 26.271 0.536 1.012 CVT-F 5.386 33.505 8.058 1.005 4.4. Đánh giá kết quả khi tiến hành xử lý ảnh y tế (ảnh MRI não bộ) Kết quả thực nghiệm thu được như hình 6 và bảng 2. Hình 6. So sánh ngoại quan và mật độ phổ năng lượng của ảnh MRI não bộ. Bảng 2. Kết quả định lượng chất lượng ảnh MRI não bộ. Method RMSE PSNR Entropi SC DnCNN 10.595 27.629 6.183 1.093 DWT 40.113 16.065 0.001 1.250 Kuan 12.946 25.888 6.898 1.079 Frost 13.625 25.444 6.771 1.049 DTCWT 17.876 23.085 0.723 1.034 CVT-F 9.853 28.260 7.011 1.003 4.5. Đánh giá kết quả khi tiến hành xử lý ảnh siêu phổ Hình ảnh siêu phổ, giống như hình ảnh quang phổ khác, thu thập và xử lý thông tin từ trên quang phổ điện từ. Mục đích của ảnh siêu phổ là để có được quang phổ cho mỗi điểm ảnh trong hình ảnh của một cảnh, với mục đích của việc tìm kiếm các đối tượng, xác định vật liệu, hoặc phát hiện các quy trình. Kết quả thực nghiệm thu được như hình 7 và bảng 3. Ảnh gốc DnCNN DWT Kuan Ảnh gốc DnCNN DWT Kuan Frost DT-CWT CVT-F Frost DT-CWT CVT-F Ảnh gốc DnCNN DWT Kuan Ảnh gốc DnCNN DWT Kuan Frost DT-CWT CVT-F Frost DT-CWT CVT-F Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 117 Hình 7. So sánh ngoại quan và mật độ phổ năng lượng của ảnh siêu phổ. Bảng 3. Kết quả định lượng chất lượng ảnh siêu phổ. Method RMSE PSNR Entropi SC DnCNN 9.194 28.861 7.803 1.069 DWT 67.146 11.590 0.044 1.250 Kuan 12.982 25.864 7.881 1.069 Frost 9.699 28.397 7.844 1.065 DTCWT 15.274 24.452 0.057 1.014 CVT-F 6.902 31.352 8.000 0.983 4.6. Đánh giá kết quả khi tiến hành xử lý ảnh SAR Ảnh radar cung cấp nhiều thông tin về đất, nước, rừng,... Với ảnh thực nghiệm là ảnh SAR, kết quả được thể hiện trong hình 8 và bảng 4. Hình 8. So sánh ngoại quan và mật độ phổ năng lượng của ảnh SAR. Bảng 4. Kết quả định lượng chất lượng ảnh SAR. Method RMSE PSNR Entropi SC DnCNN 11.483 26.930 6.146 1.188 DWT 30.683 18.393 0.000 1.248 Kuan 13.952 25.238 6.388 1.197 Frost 13.012 25.844 6.199 1.178 DTCWT 21.588 21.447 0.226 1.043 CVT-F 10.833 27.964 7.001 1.010 Đánh giá kết quả thực nghiệm: Chúng ta có thể thấy rằng, kết quả trực quan theo phương pháp đề xuất thể hiện chất lượng hình ảnh rất tốt. Ảnh khôi phục với phương pháp đề xuất cho độ nhạy sáng tốt hơn và khả năng quan sát rõ ràng hơn. Đối với mật độ phổ năng lượng, ảnh chất lượng thấp sẽ cho một mật độ năng lượng quang phổ phẳng. Do đó, từ các kết quả trên, dễ dàng thấy rằng phương pháp đề xuất cho chất lượng xử lý tốt nhất bởi vì mật độ năng lượng phổ càng lớn cho thấy kết quả tăng cường ảnh càng tốt. Công nghệ thông tin & Cơ sở toán học cho tin học 118 Đ. P. T. Hương, N. T. Anh, D. T. Bình, “Nâng cao chất lượng ảnh dựa trên biến đổi Curvelet.” Đối với các tham số đánh giá chất lượng ảnh đã lựa chọn, kết quả thực nghiệm đã chỉ ra rằng phương pháp đề xuất đã cho chất lượng hình ảnh tốt hơn so với các phương pháp khác, cụ thể: RMSE càng nhỏ càng tốt, PSNR càng lớn càng tốt, Entropi càng lớn càng tốt, và SC càng nhỏ càng tốt. 4. KẾT LUẬN Trong bài báo này, phương pháp đề xuất thu được kết quả có hiệu suất tốt về các thông số RMSE, PSNR, Entropi, SC, đồng thời, thời gian thực thi thực tế rất nhanh so với các phương pháp được giới thiệu, thậm chí so với một phương pháp tiên tiến của mạng nơ ron DnCNN nó cũng cho thấy khả năng xử lý tốt hơn. Curvelet là phương pháp ngày càng được ứng dụng rộng rãi trong thực tế. Trong tương lai các nghiên cứu tiếp theo sẽ tiếp tục cải tiến, tạo ra các phương pháp lai dựa trên Curvelet để tăng cường hơn nữa chất lượng xử lý và bổ sung thêm sự lựa chọn phong phú về giải pháp cho các lĩnh vực liên quan. TÀI LIỆU THAM KHẢO [1]. Mallat, S. (1989), “A theory for multiresolution signal decomposition: the wavelet representation,” IEEE Pattern Anal. and Machine Intell., vol. 11, no. 7, pp. 674–693. [2]. J. Jennifer Ranjani and S. J. Thiruvengadam, “Dual-Tree Complex Wavelet Transform Based SAR Despeckling Using Interscale Dependence” IEEE Transactions On Geoscience And Remote Sensing, vol. 48, no. 6, June 2010. [3]. C. Dong, C. C. Loy, and X. Tang. “Accelerating the super-resolution convolutional neural network”. In ECCV, pages 391–407, 2016. 3. [4]. V. S. Frost, J. A. Stiles, K. S. Shanmugan, J. C. Holtzman. “A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise”. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 4, no. 2, pp. 157,166, 1982. [5]. J. N. Ellinas, T. Mandadelis, and A. Tzortzis, “The statistical modeling of wavelet coefficients as a tool for image de-noising,” in Proceedings of the 2nd International Conference on Information Technology and Quality, 2005. [6]. C. Patvardan, A.K.Verma, C.VLakshmi, "Denoising of Document Images using Discrete Curvelet Transform for OCR Applications" International Journal of Computer Applications 2012. [7]. Yang Wang and Haomin Zhou, “Total Variation Wavelet-Based Medical Image Denoising”, International Journal of Biomedical Imaging, Hindawi Publication, Volume 2006 Article ID89095, pages 1-6, 2006. ABSTRACT IMAGE QUALITY ENHANCEMENT BASED ON CURVELET Visual information transmitted in a digital image is becoming a major means of communication, but the images that are received, encoded and transmitted are often damaged by noise or vibration. Several techniques have been proposed to improve image quality, such as discrete Wavelet transform, dual-tree complex Wavelet transform, traditional filters, pretrained denoising convolutional neural network, etc. However, it can still not bring high efficiency due to high noise, computational complexity, memory consumption, and processing speed. In this article, we propose to use Curvelet transform to improve image quality. Keywords: Curvelet Transforms; Image Denoising; Dual Tree Complex Wavelet Transform. Nhận bài ngày 19 tháng 11 năm 2020 Hoàn thiện ngày 01 tháng 3 năm 2021 Chấp nhận đăng ngày 12 tháng 4 năm 2021 Địa chỉ: 1Trường Lao động xã hội; 2Trường Đại học Bách Khoa Hà Nội; 3Trường Đại học Điện lực. *Email: Binhdt@epu.edu.vn.
File đính kèm:
 nang_cao_chat_luong_anh_dua_tren_bien_doi_curvelet.pdf
nang_cao_chat_luong_anh_dua_tren_bien_doi_curvelet.pdf

