Mô hình thuật phóng trong của hệ súng phóng lựu có tính đến thuốc phóng cháy không hoàn toàn trong buồng cao áp

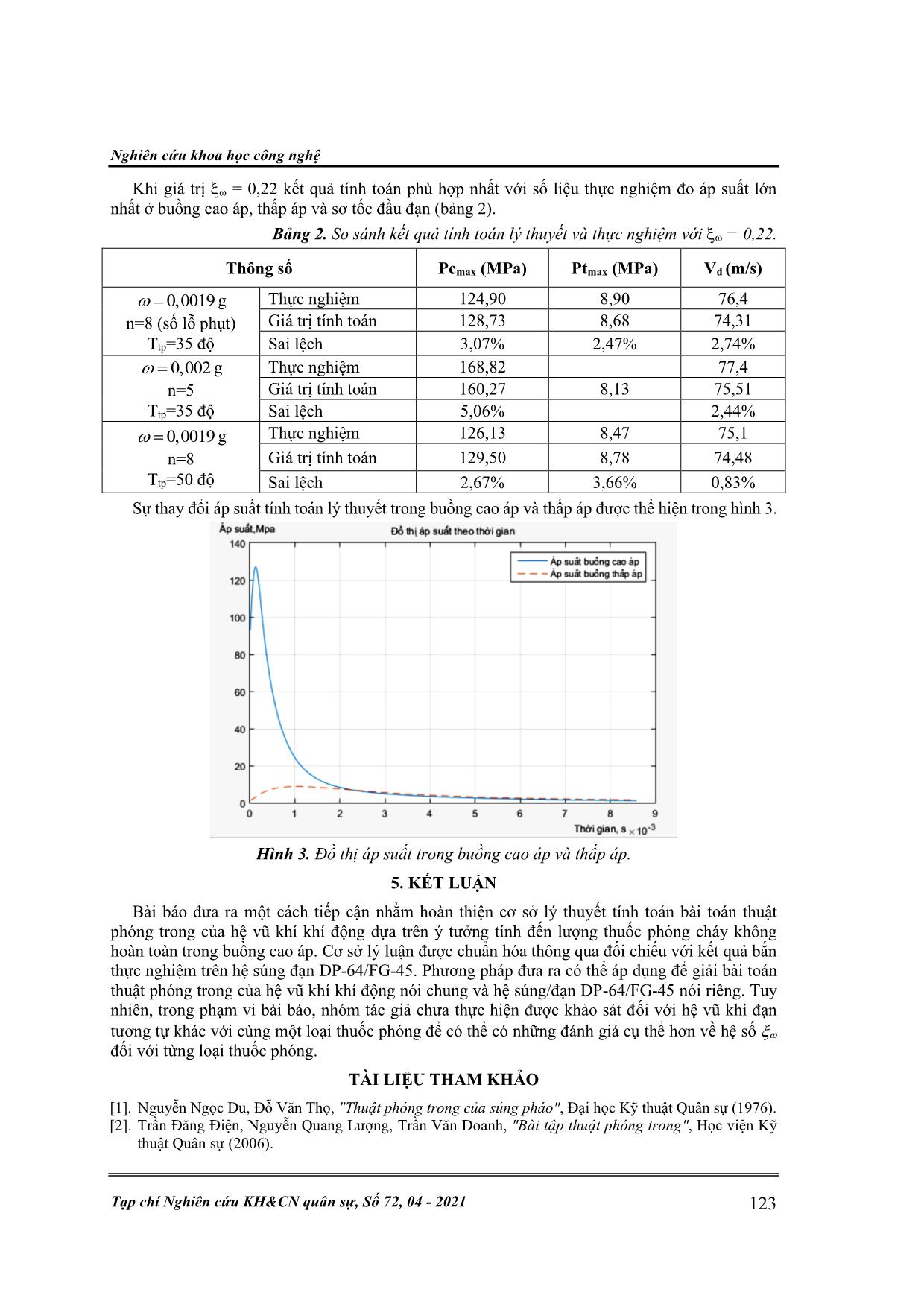
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 119 
MÔ HÌNH THUẬT PHÓNG TRONG CỦA HỆ SÚNG PHÓNG LỰU 
CÓ TÍNH ĐẾN THUỐC PHÓNG CHÁY KHÔNG HOÀN TOÀN 
TRONG BUỒNG CAO ÁP 
Nguyễn Hanh Hoàn1*, Trần Đức Việt2, Ninh Đức Sinh2 
Phan Văn Tuấn3, Nguyễn Thanh Điền3, Nguyễn Văn Quân3 
Mô hình thuật phóng hai buồng cao-thấp áp được sử dụng rộng rãi trong các hệ súng 
phóng lựu với giả thiết thuốc phóng cháy hoàn toàn trong buồng cao áp. Tuy nhiên, thực 
tế sẽ có một lượng thuốc phóng cháy không hoàn toàn trong buồng cao áp, bị phụt ra và 
tiếp tục cháy trong buồng thấp áp nên giả thiết trên sẽ dẫn tới sai số tính toán và phải hiệu 
chỉnh bằng các hệ số khớp. Do vậy, bài báo này đề xuất mô hình thuật phóng hệ súng 
phóng lựu trong đó có kể đến hiện tượng dòng hỗn hợp phụt từ buồng cao áp sang buồng 
thấp áp là dòng hai pha gồm khí thuốc và các hạt thuốc phóng chưa cháy hết, các hạt 
thuốc này tiếp tục cháy trong buồng thấp áp. Mục đích đưa ra mô hình nhằm hoàn thiện 
hơn cơ sở lý thuyết và đa dạng hóa cách tiếp cận khi giải bài toán thuật phóng trong của 
hệ súng phóng lựu. Tính toán và thử nghiệm đối với hệ súng DP-64 và đạn FG-45 cho hệ 
số không cháy của thuốc phóng trong buồng cao áp là 0,22. 
Từ khóa: Thuật phóng trong; Vũ khí khí động; Súng phóng lựu. 
1. ĐẶT VẤN ĐỀ 
Quá trình thuật phóng trong của hệ vũ khí khí động (có hai buồng cao áp/thấp áp) bao gồm 
các hiện tượng vật lý cơ bản: sự cháy và tạo khí của thuốc phóng trong buồng cao áp; phụt khí từ 
buồng cao áp sang buồng thấp áp; chuyển động của đầu đạn trong nòng. Hiện nay, khi giải bài 
toán thuật phóng trong của hệ súng phóng lựu, chúng ta đều tiếp cận theo hướng giả thiết rằng 
thuốc phóng cháy hoàn toàn trong buồng cao áp, các sai số được hiệu chỉnh thông qua hai hệ số 
khớp cơ bản: kể đến lượng thuốc phóng cháy không hoàn toàn trong buồng cao áp thông qua hệ 
số giảm lực thuốc phóng , khi đó lực thuốc phóng được tính theo biểu thức [1,2]: f=.fo với  < 
1 và hệ số kể đến tổn thất năng lượng trong quá trình phụt khí qua lỗ 2 < 1. Với cách giải quyết 
này, hệ phương trình toán học mô tả quá trình thuật phóng trong của súng phóng lựu có buồng 
cao-thấp áp như sau [1]: 
c
k
pdz
dt I
= (1) 
2(1 2 3 )
d dz
z z
dt dt

  = + + (2) 
2 0. . ( )
. .
t c t
c
K S p pd
dt f

 
−
= (3) 
(1 ). ( 1). .c c
c
d d
k
d dt dt
dt
 
 

 
− − −
=
−
 (4) 
Wc = W0c - (1-). ( ). .

  

− − (5) 
pc = 
. . .( )c
c
f
W
   −
 (6) 
( . ). . . .c t d
t
d dv
k K v
d dt dt
dt

  


− −
= (7) 
Cơ kỹ thuật & Cơ khí động lực 
 120 N. H. Hoàn, , N. V. Quân, “Mô hình thuật phóng trong của hệ súng  buồng cao áp.” 
Wt = W0t - .. + S.l (8) 
pt = 
. . . t
t
f
W

 (9) 
. .
.
tS p gdv
dt q
= (10) 
dl
v
dt
= (11) 
Với (1), (2) là các phương trình mô tả quá trình cháy và tạo khí của thuốc phóng; (3) là 
phương trình phụt khí qua loa phụt; (4), (7) là các phương trình năng lượng; (5), (6), (8), (9) là 
các phương trình trạng thái; (10), (11) là các phương trình chuyển động của đạn. 
Trong đó: 
z là bề dày cháy tương đối của thuốc phóng; 
pc, pt lần lượt là áp suất khí thuốc trong buồng cao áp và buồng thấp áp; 
Ik là xung lượng toàn phần của áp suất khí thuốc; 
, ,  là các đặc trưng hình hạng của thuốc phóng; 
 là lượng thuốc phóng đã cháy tương đối; 
 là lượng phụt khí tương đối; 
1
1 .
c
a
b


= −
+
 là nhiệt độ tương đối của khí thuốc trong buồng cao áp, với a=0,3; b =5,0; 
τt là nhiệt độ tương đối trong buồng thấp áp; 
K0 = 
1
2( 1)2
. .
1
k
k
g k
k
+
− 
+ 
 với k là số mũ đoạn nhiệt; 
Kd = 
.
. .
q
f g


 là hệ số tăng nặng với θ = k-1; 
f là lực thuốc phóng; 
ω là khối lượng thuốc phóng; 
α là lượng cộng tích; 
St, S lần lượt là tiết diện cửa ra của loa phụt và tiết diện ngang lòng nòng; 
 là hệ số tính công thứ yếu; 
Wc, Wt lần lượt là thể tích của khí thuốc sinh ra trong buồng cao áp và buồng thấp áp; 
W0c, W0t lần lượt là thể tích tự do buồng cao áp và buồng thấp áp. 
Việc sử dụng các hệ số phù hợp  và 2 đã được hiện thực hóa và chứng minh tính đúng đắn 
thông qua sự so sánh giữa đường cong lý thuyết và thực nghiệm. Tuy nhiên, nhằm hoàn thiện 
hơn cơ sở lý thuyết tính toán và đa dạng hóa cách thức tiếp cận ta có thể xây dựng mô hình toán 
học quá trình thuật phóng trong có kể đến hiện tượng thuốc phóng cháy không hoàn toàn trong 
buồng cao áp. 
2. MÔ HÌNH LÝ THUYẾT 
Để giải quyết bài toán theo hướng này, ta giả thiết rằng có một phần thuốc phóng không cháy 
trong buồng cao áp, bị chảy theo dòng sản phẩm khí ra rồi cháy trong buồng thấp áp, được tính 
bằng biểu thức: 2=.o, trong đó, o là tổng khối lượng thuốc phóng, 0 < < 1 ta gọi là hệ số 
không cháy của thuốc phóng. Do áp suất trong buồng thấp áp nhỏ nên số thuốc phóng này sẽ 
không cháy theo quy luật tuyến tính một số hạng (phương trình (1) mà sẽ cháy theo quy luật hàm 
số mũ, phương trình biểu diễn quy luật cháy của lượng thuốc phóng này là [1-3]: 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 121 
2 t
k
pdz
dt I

= (1’) 
Phương trình (1’) khác so với (1) ở chỗ: áp suất lúc này là trong buồng thấp áp chỉ khoảng vài 
MPa, do vậy, quy luật cháy có dạng hàm số mũ, số mũ quy luật cháy  phụ thuộc vào tính chất, 
nhiệt độ ban đầu của thuốc phóng và được tra cứu theo áp suất trong nòng pt [1]. 
Theo hướng tiếp cận này, các hiện tượng thuật phóng diễn ra bao gồm: quá trình cháy tạo khí 
của thuốc phóng trong buồng cao áp; sự chảy của sản phẩm cháy và thuốc phóng từ buồng cao 
áp ra buồng thấp áp; sự cháy và tạo khí của thuốc phóng trong buồng thấp áp; chuyển động của 
đầu đạn. Như vậy, buồng thấp áp ngoài việc được bổ sung sản phẩm khí từ buồng cao áp còn 
được tăng cường sản phẩm cháy do lượng thuốc phóng 2 cháy liên tục tạo ra. Hệ phương trình 
toán học mô tả các hiện tượng thuật phóng trong diễn ra sẽ bao gồm: 
1. Toàn bộ các phương trình từ (1) đến (6), chỉ khác ở chỗ lượng thuốc phóng khi này sẽ là 
phần thuốc cháy hoàn toàn trong buồng cao áp: 1 = (1-).o; 
2. Bổ sung các phương trình biểu diễn sự cháy, sinh khí của phần thuốc phóng trong buồng 
thấp áp: 
2 t
k
pdz
dt I

= (1’) 
22 2
2 2(1 2 3 )
d dz
z z
dt dt

  = + + (2’) 
3. Các phương trình (7, 8, 9) sẽ thay đổi do kể đến phần khí thuốc sinh ra bởi sự cháy của 
thuốc phóng trong buồng cao áp, cụ thể: 
2
2
(1 ) ( . ). . . .t c t d
t
d d dv
k K v
d dt dt dt
dt
 
   

 
− + − −
=
+
 (7’) 
Wt = W0t - .o ((1-).+ .2) + S.l (8’) 
pt = 2
. ((1 ). . ).o t
t
f
W
      − + (9’) 
Để chính xác hóa hệ số không cháy hết của thuốc phóng, ta tiến hành giải bài toán với các giá 
trị  khác nhau rồi so sánh với kết quả thực nghiệm. 
3. THỰC NGHIỆM 
3.1. Súng và đạn thử nghiệm 
Nhóm tác giả đã tiến hành bắn thử nghiệm trên súng phóng lựu chống người nhái DP-64, đạn 
chống người nhái FG-45, lấy số liệu và so sánh với kết quả tính toán lý thuyết để chuẩn xác hóa 
giá trị . 
Hình 1. Súng DP-64 và đạn FG-45 chống người nhái [4]. 
Cơ kỹ thuật & Cơ khí động lực 
 122 N. H. Hoàn, , N. V. Quân, “Mô hình thuật phóng trong của hệ súng  buồng cao áp.” 
Bảng 1. Các thông số thuật phóng cơ bản của hệ súng DP-64 và đạn FG-45 [4]. 
Thông số Giá trị 
Cỡ đạn (nòng), mm 45 
Khối lượng phần bay, kg 0,5 
Sơ tốc, m/s 74 
Thuốc phóng Thuốc phóng cầu C-K59 
Đường kính tiết diện tới hạn của loa phụt, mm 2,5 
Số lượng lỗ phụt 8 
Các hệ số tổn hao 2 = 0,78; ω = 0,22 
Quãng đường đạn chuyển động trong nòng, mm l =415 
Thể tích buồng đốt cao áp ban đầu, mm3 8877 
Thể tích buồng thấp áp ban đầu, mm3 144166 
Trọng lượng thuốc phóng, kG 1,82 x 10-3 
3.2. Thiết bị đo 
- Đo áp suất lớn nhất trong buồng thấp áp bằng Cruse và trụ đồng Φ6x9,8 dự áp 50 kG/cm2; 
- Đo áp suất buồng cao áp bằng piezo 6215 Kistler và thiết bị đo thuật phóng BA04SE; 
- Đo sơ tốc đo bằng bia quang B462 và thiết bị đo BA04SE. 
3.3. Bố trí thử nghiệm 
Sơ đồ bố trí thử nghiệm tại hầm bắn như trong hình 2 [4]. 
Hình 2. Bố trí thử nghiệm đo áp suất trong buồng cao-thấp áp và sơ tốc. 
4. KẾT QUẢ TÍNH TOÁN, THỬ NGHIỆM 
Giải hệ phương trình vi phân trên bằng phần mềm Matlab trên cơ sở thuật toán Rungge - 
Kutta với các giá trị thay đổi của  trong khoảng 0 < < 1. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 123 
Khi giá trị  = 0,22 kết quả tính toán phù hợp nhất với số liệu thực nghiệm đo áp suất lớn 
nhất ở buồng cao áp, thấp áp và sơ tốc đầu đạn (bảng 2). 
Bảng 2. So sánh kết quả tính toán lý thuyết và thực nghiệm với  = 0,22. 
Thông số Pcmax (MPa) Ptmax (MPa) Vd (m/s) 
0,0019 = g 
n=8 (số lỗ phụt) 
Ttp=35 độ 
Thực nghiệm 124,90 8,90 76,4 
Giá trị tính toán 128,73 8,68 74,31 
Sai lệch 3,07% 2,47% 2,74% 
0,002 = g 
n=5 
Ttp=35 độ 
Thực nghiệm 168,82 77,4 
Giá trị tính toán 160,27 8,13 75,51 
Sai lệch 5,06% 2,44% 
0,0019 = g 
n=8 
Ttp=50 độ 
Thực nghiệm 126,13 8,47 75,1 
Giá trị tính toán 129,50 8,78 74,48 
Sai lệch 2,67% 3,66% 0,83% 
Sự thay đổi áp suất tính toán lý thuyết trong buồng cao áp và thấp áp được thể hiện trong hình 3. 
Hình 3. Đồ thị áp suất trong buồng cao áp và thấp áp. 
5. KẾT LUẬN 
Bài báo đưa ra một cách tiếp cận nhằm hoàn thiện cơ sở lý thuyết tính toán bài toán thuật 
phóng trong của hệ vũ khí khí động dựa trên ý tưởng tính đến lượng thuốc phóng cháy không 
hoàn toàn trong buồng cao áp. Cơ sở lý luận được chuẩn hóa thông qua đối chiếu với kết quả bắn 
thực nghiệm trên hệ súng đạn DP-64/FG-45. Phương pháp đưa ra có thể áp dụng để giải bài toán 
thuật phóng trong của hệ vũ khí khí động nói chung và hệ súng/đạn DP-64/FG-45 nói riêng. Tuy 
nhiên, trong phạm vi bài báo, nhóm tác giả chưa thực hiện được khảo sát đối với hệ vũ khí đạn 
tương tự khác với cùng một loại thuốc phóng để có thể có những đánh giá cụ thể hơn về hệ số  
đối với từng loại thuốc phóng. 
TÀI LIỆU THAM KHẢO 
[1]. Nguyễn Ngọc Du, Đỗ Văn Thọ, "Thuật phóng trong của súng pháo", Đại học Kỹ thuật Quân sự (1976). 
[2]. Trần Đăng Điện, Nguyễn Quang Lượng, Trần Văn Doanh, "Bài tập thuật phóng trong", Học viện Kỹ 
thuật Quân sự (2006). 
Cơ kỹ thuật & Cơ khí động lực 
 124 N. H. Hoàn, , N. V. Quân, “Mô hình thuật phóng trong của hệ súng  buồng cao áp.” 
[3]. Ngô Văn Giao, "Tính chất thuốc phóng và nhiên liệu tên lửa", NXB Quân đội nhân dân (2005). 
[4]. Viện Vũ khí, “Hồ sơ đề tài súng và đạn lựu phóng chống người nhái,” (2020). 
ABSTRACT 
THE INTERIOR BALLISTICS MODEL OF THE GRENADE LAUNCHER SYSTEM 
WITH THE PHENOMENON OF PROPELLANT POWDER BURNING INCOMPLETELY 
IN HIGH-PRESSURE CHAMBER 
 The model of Interior ballistics with high-low pressure chambers is used popularly in 
the grenade launchers with the assumption: Propellant powder completely burning into 
gases. However, the reality is there’s a bit of Propellant powder burning incompletely in a 
high-pressure chamber and flow through one or more nozzles (orifices) in the low-
pressure chamber and keep burning. Therefore, the above assumption will lead to 
calculation errors and must be corrected by matching coefficients. This article proposes a 
grenade launch system model, which includes the phenomenon of jet-outflow from a high-
pressure chamber to a low-pressure chamber is a two-phase flow of gas and incomplete 
burning particles; these particles continue to burn in the low-pressure chamber. The 
purpose of the model is to improve the theoretical basis and diversify the approach when 
solving the Interior ballistics of grenade launchers. Calculation and testing for the system 
of DP-64 gun and FG-45 ammunition for the incomplete burning coefficient of the 
Propellant in the high-pressure chamber is 0,22. 
Keywords: The interior ballistics; Dynamic weapons; The grenade launchers. 
 Nhận bài ngày 29 tháng 7 năm 2020 
Hoàn thiện ngày 01 tháng 3 năm 2021 
Chấp nhận đăng ngày 12 tháng 3 năm 2021 
Địa chỉ: 1Viện Tên lửa/Viện KHCNQS; 
2Viện Vũ khí/Tổng cục CNQP; 
3Học viện KTQS. 
*Email: hanhhoanvtl@gmail.com.