Kỹ thuật chỉ dẫn cho giải thuật tiến hóa đa mục tiêu sử dụng mô hình đại diện
Tóm tắt: Trong thực tế, có nhiều bài toán đa mục tiêu (Multi-objective problems -
MOPs) khó, nếu giải bằng phương pháp thông thường, kể cả sử dụng giải thuật tiến hóa,
vẫn gặp phải nhiều thách thức như: hàm mục tiêu khó mô hình hóa, chi phí tính toán lớn,
tài nguyên tính toán có hạn, Ý tưởng chung để giải quyết các bài toán khó này là làm
đơn giản hóa, tách ra thành các bài toán con. Có hai phương pháp phổ biến để thực hiện
ý tưởng đó là mô phỏng và sử dụng mô hình xấp xỉ. Trong đó, mô hình xấp xỉ, còn gọi là
mô hình đại diện (surrogate model), sử dụng hàm đại diện thay thế cho hàm mục tiêu gốc
tỏ ra khá hiệu quả, dễ thực hiện, phù hợp với các bài toán thực tế.
Giải thuật tiến hóa đa mục tiêu (Multi-objective evolutionary algorithms - MOEAs) sử
dụng mô hình đại diện đang được nhiều nhà nghiên cứu quan tâm. Việc duy trì sự cân
bằng giữa khả năng thăm dò (exploration) và khai thác (exploitation) trong quá trình tiến
hóa cũng như cân bằng giữa chất lượng hội tụ (convergence) và đa dạng (diversity) của
quần thể giải pháp là vấn đề nghiên cứu hết sức cần thiết nhằm nâng cao chất lượng, duy
trì tính bền vững của giải thuật. Bài báo tập trung đánh giá một số yếu tố tác động đến
chất lượng, hiệu quả của giải thuật, đồng thời phân tích kỹ thuật chỉ dẫn, tác động của các
tham số điều khiển quá trình tiến hóa. Từ đó, đề xuất các kỹ thuật chỉ dẫn để nâng cao
chất lượng giải thuật thông qua các cơ chế thích ứng, quá trình tiến hóa tự điều chỉnh.
Thông qua thử nghiệm với các bài toán mẫu tiêu biểu, sử dụng các độ đo phổ biến, kết
quả đã chứng minh tính hiệu quả của các kỹ thuật chỉ dẫn, góp phần tạo ra những phiên
bản giải thuật mới giải quyết tốt hơn các bài toán khó.

Trang 1

Trang 2

Trang 3

Trang 4
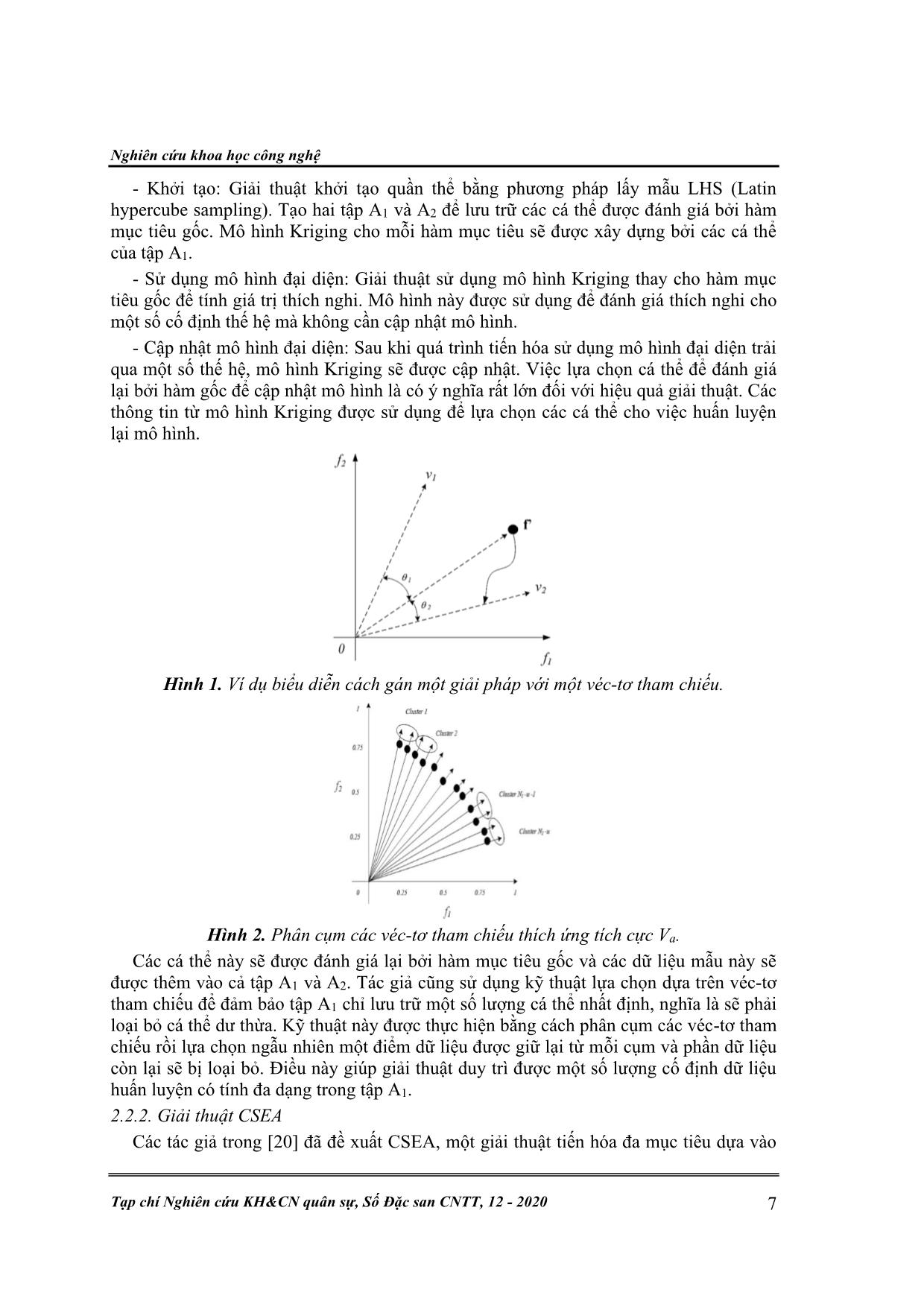
Trang 5

Trang 6
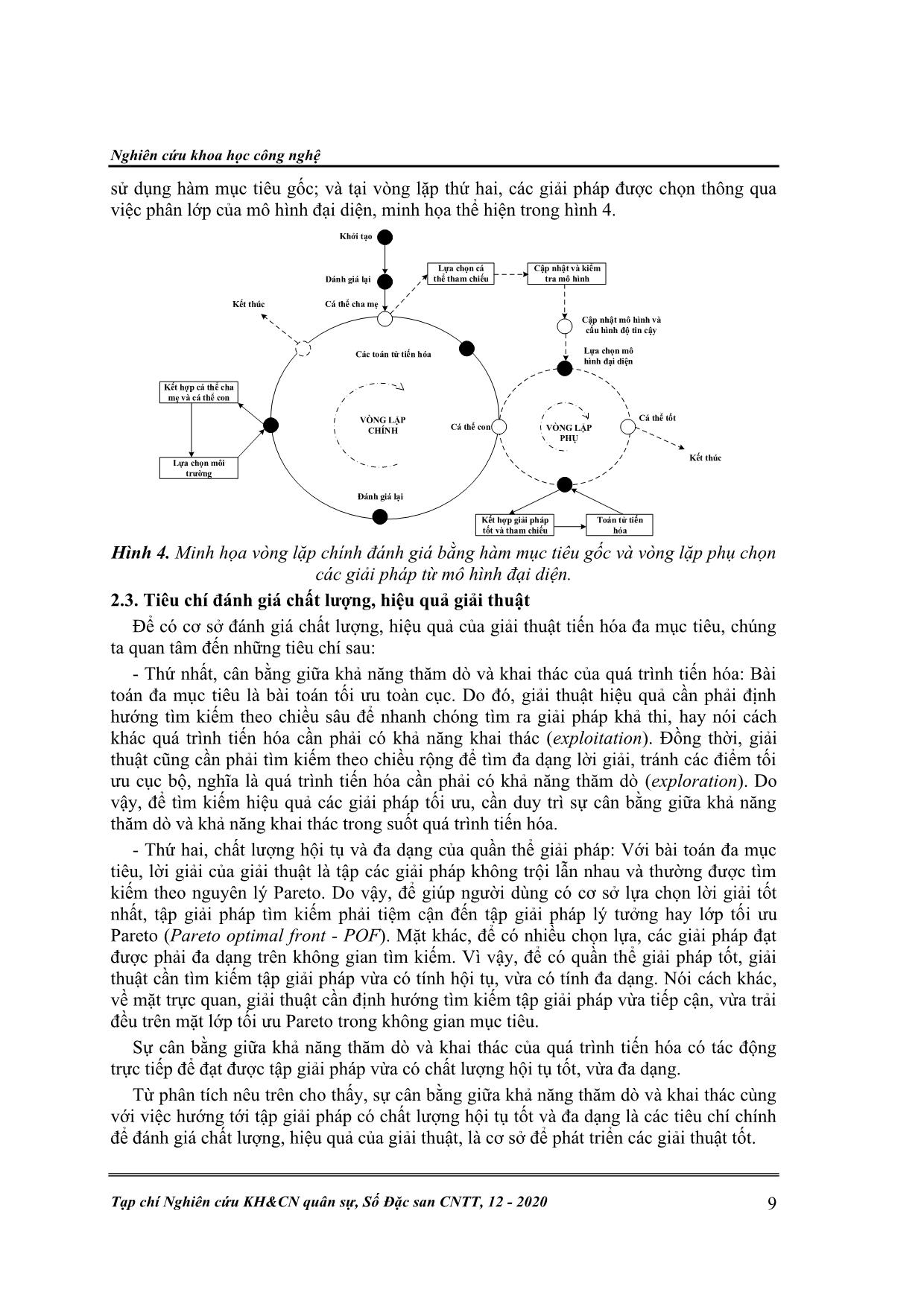
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Kỹ thuật chỉ dẫn cho giải thuật tiến hóa đa mục tiêu sử dụng mô hình đại diện

Nghiên cứu khoa học công nghệ
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 3
KỸ THUẬT CHỈ DẪN CHO GIẢI THUẬT TIẾN HÓA ĐA MỤC TIÊU
SỬ DỤNG MÔ HÌNH ĐẠI DIỆN
Nguyễn Đức Định1*, Nguyễn Long2, Thái Trung Kiên1
Tóm tắt: Trong thực tế, có nhiều bài toán đa mục tiêu (Multi-objective problems -
MOPs) khó, nếu giải bằng phương pháp thông thường, kể cả sử dụng giải thuật tiến hóa,
vẫn gặp phải nhiều thách thức như: hàm mục tiêu khó mô hình hóa, chi phí tính toán lớn,
tài nguyên tính toán có hạn, Ý tưởng chung để giải quyết các bài toán khó này là làm
đơn giản hóa, tách ra thành các bài toán con. Có hai phương pháp phổ biến để thực hiện
ý tưởng đó là mô phỏng và sử dụng mô hình xấp xỉ. Trong đó, mô hình xấp xỉ, còn gọi là
mô hình đại diện (surrogate model), sử dụng hàm đại diện thay thế cho hàm mục tiêu gốc
tỏ ra khá hiệu quả, dễ thực hiện, phù hợp với các bài toán thực tế.
Giải thuật tiến hóa đa mục tiêu (Multi-objective evolutionary algorithms - MOEAs) sử
dụng mô hình đại diện đang được nhiều nhà nghiên cứu quan tâm. Việc duy trì sự cân
bằng giữa khả năng thăm dò (exploration) và khai thác (exploitation) trong quá trình tiến
hóa cũng như cân bằng giữa chất lượng hội tụ (convergence) và đa dạng (diversity) của
quần thể giải pháp là vấn đề nghiên cứu hết sức cần thiết nhằm nâng cao chất lượng, duy
trì tính bền vững của giải thuật. Bài báo tập trung đánh giá một số yếu tố tác động đến
chất lượng, hiệu quả của giải thuật, đồng thời phân tích kỹ thuật chỉ dẫn, tác động của các
tham số điều khiển quá trình tiến hóa. Từ đó, đề xuất các kỹ thuật chỉ dẫn để nâng cao
chất lượng giải thuật thông qua các cơ chế thích ứng, quá trình tiến hóa tự điều chỉnh.
Thông qua thử nghiệm với các bài toán mẫu tiêu biểu, sử dụng các độ đo phổ biến, kết
quả đã chứng minh tính hiệu quả của các kỹ thuật chỉ dẫn, góp phần tạo ra những phiên
bản giải thuật mới giải quyết tốt hơn các bài toán khó.
Từ khóa: Kỹ thuật chỉ dẫn; Mô hình đại diện; Kriging; Giải thuật tiến hóa đa mục tiêu.
1. ĐẶT VẤN ĐỀ
Các bài toán tối ưu trong thực tế thường có nhiều mục tiêu xung đột với nhau. Bài
toán đòi hỏi tìm kiếm các giải pháp tối ưu cho các mục tiêu một cách đồng thời. Bài toán
đó được định nghĩa là bài toán tối ưu đa mục tiêu hay bài toán đa mục tiêu và được biểu
diễn như sau [10]:
minimize {f1(x), f2(x),, fk(x)} x S (1)
Trong đó: k (≥ 2) là số mục tiêu, fi : Rn → R là hàm mục tiêu (i =1, 2,, k).
Véc-tơ các hàm mục tiêu được ký hiệu là f(x) = (f1(x), f2(x),, fk(x))T. Véc-tơ biến hay
véc-tơ quyết định được ký hiệu là x = (x1, x2,, xn)T thuộc vùng (tập hợp) khả thi S, là
không gian con của không gian biến Rn (không gian quyết định). Thuật ngữ “minimize”
có nghĩa là tất cả các hàm mục tiêu được cực tiểu hóa đồng thời. Nếu không có sự xung
đột giữa các hàm mục tiêu, thì một giải pháp có thể tìm được thỏa mãn mọi hàm mục tiêu
là tối ưu. Trong trường hợp này, không cần đến một phương pháp đặc biệt nào để giải
quyết. Để tránh trường hợp tầm thường này, giả sử rằng, không tồn tại một giải pháp tối
ưu cho tất cả các mục tiêu, có nghĩa là các hàm mục tiêu ít nhất xung đột nhau một phần.
Bài toán đa mục tiêu thường có hai hoặc ba mục tiêu, nhưng trong thực tế có nhiều
bài toán phức tạp với các đặc điểm như: nhiều mục tiêu, không gian tìm kiếm lớn, hàm
mục tiêu khó, do đó, độ phức tạp tính toán lớn, thậm chí là “hộp đen” không mô hình
hóa được về toán học. Các bài toán mang đặc điểm đó được xếp vào lớp bài toán đa mục
tiêu khó, chi phí lớn (bài toán đa mục tiêu khó).
Công nghệ thông tin
4 N. Đ. Định, N. Long, T. T. Kiên, “Kỹ thuật chỉ dẫn cho giải thuật mô hình đại diện.”
Với bài toán đa mục tiêu thông thường, giải thuật tiến hóa khá phù hợp, hiệu quả và
được gọi là giải thuật tiến hóa đa mục tiêu. Giải thuật có nhiều ưu điểm như: Làm việc
trên quần thể, sử dụng cơ chế tiến hóa, làm việc theo cơ chế ngẫu nhiên, xấp xỉ, nên có
thể giải được hầu hết các bài toán, kể cả bài toán không khả vi. Tuy vậy, với lớp bài toán
đa mục tiêu khó, giải thuật gặp nhiều khó khăn.
Để giải các bài toán đa mục tiêu khó, chúng ta có thể sử dụng một số phương pháp
phổ biến như: mô phỏng, phân hoạch, sử dụng mô hình xấp xỉ. Trong phương pháp mô
phỏng, với các kỹ thuật máy tính, không gian tìm kiếm được biểu diễn trực quan và
người dùng sẽ quan sát, lựa chọn một hoặc nhiều giải pháp tối ưu. Phương pháp này có
ưu điểm là trực quan và vai trò của người dùng rất quan trọng, có tính quyết định. Tuy
vậy, để sử dụng phương pháp này đòi hỏi nhiều chi phí và kiến thức chuyên gia của
người dùng. Trong phương pháp phân hoạch, bài toán được phân chia thành các bài toán
con, đơn giản hơn. Các bài toán con được giải đồng thời để tạo ra tập giải pháp tối ưu.
Phương pháp này tương đối hiệu quả, nhưng có nhiều bài toán, việc phân hoạch thành
các bài toán con là rất khó, thậm chí không thể phân hoạch. Còn phương pháp sử dụng
mô hình xấp xỉ (mô hình đại diện) với các kỹ th ... 0,0004 0,0004 0,0003
DTLZ8
M-CSEA 0,0527 0,0153 0,0153 0,0153 0,0153 0,0153 0,0153 0,0153 0,0153 0,0153
CSEA 0,0586 0,0173 0,0173 0,0173 0,0173 0,0173 0,0173 0,0173 0,0173 0,0173
Công nghệ thông tin
18 N. Đ. Định, N. Long, T. T. Kiên, “Kỹ thuật chỉ dẫn cho giải thuật mô hình đại diện.”
Các hình 6, 7 biểu diễn quá trình tìm kiếm giải pháp của các giải thuật đề xuất so sánh
với các giải thuật gốc.
- So sánh quá trình tối ưu của giải thuật đề xuất M-K-RVEA và giải thuật gốc K-
RVEA thể hiện tại hình 6.
Hình 6. Quá trình tối ưu của M-K-RVEA và K-RVEA với bài toán DTLZ1.
- So sánh quá trình tối ưu của giải thuật đề xuất M-CSEA và giải thuật gốc CSEA thể
hiện tại hình 7.
Hình 7. Quá trình tối ưu của M-CSEA và CSEA với bài toán DTLZ8.
Qua các kết quả thử nghiệm, chúng tôi có nhận xét như sau:
Với giải thuật M-K-RVEA, so sánh kết quả thử nghiệm với giải thuật gốc K-RVEA
thấy rằng M-K-RVEA sử dụng kỹ thuật chỉ dẫn, tự động điều chỉnh tham số đã duy trì
được sự cân bằng tốt hơn giữa tính hội tụ và đa dạng của quần thể giải pháp. Cụ thể là ở
những thế hệ đầu, kết quả tốt hơn với các bài toán DTLZ1, DTLZ3, DTLZ4, DTLZ5,
DTLZ8 trên GD và DTLZ1, DTLZ3, DTLZ4, DTLZ5, DTLZ7, DTLZ9 trên IGD. Ở các
thế hệ liền sau đó, M-K-RVEA tốt hơn với các bài toán DTLZ1, DTLZ3, DTLZ4,
DTLZ5, DTLZ8, và có kết quả tương tự K-RVEA với bài toán DTLZ2 trên GD. Trên
IGD, giải thuật M-K-RVEA cũng đạt kết quả tốt hơn với các bài toán DTLZ1, DTLZ3,
DTLZ4, DTLZ5, DTLZ6, DTLZ8, DTLZ9. Ở các thế hệ cuối, M-K-RVEA đạt kết quả
tốt hơn với các bài toán DTLZ1, DTLZ3, DTLZ4, DTLZ5, DTLZ6, DTLZ8, DTLZ9
Nghiên cứu khoa học công nghệ
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 19
trên GD và DTLZ1, DTLZ4, DTLZ5, DTLZ8, DTLZ9 trên IGD. Trong một số ít trường
hợp khác, M-K-RVEA có kết quả tương tự hoặc kém không đáng kể so với K-RVEA.
Nói chung, thông qua kết quả thử nghiệm cho thấy, việc đề xuất kỹ thuật chỉ dẫn gắn
với tự động điều chỉnh tham số đã nâng cao hiệu quả của các giải thuật tiến hóa đa mục
tiêu sử dụng hàm đại diện nói chung và sử dụng mô hình Kriging nói riêng. Kết quả sử
dụng cơ chế tự động điều chỉnh tham số đã minh chứng cho giả thuyết về ảnh hưởng của
các yếu tố tiến trình thời gian, chất lượng hội tụ hiện tại của quần thể và đặc điểm của
bài toán đối với việc đảm bảo cả chất lượng hội tụ và đa dạng của quần thể, thông qua
việc duy trì cân bằng giữa khả năng thăm dò và khai thác của quá trình tiến hóa. Hiệu
quả của kỹ thuật chỉ dẫn tự động tại các giai đoạn tiến hóa còn phụ thuộc vào chất lượng
và hiệu quả ở giai đoạn trước, điều đó chứng tỏ rằng cần có sự điều chỉnh kịp thời để duy
trì sự cân bằng giữa thăm dò và khai thác. Tuy vậy, một số ít trường hợp kết quả của K-
RVEA tốt hơn M-K-RVEA (dù chỉ tốt hơn một chút) cũng đặt ra cho chúng ta một vài
vấn đề như sự ổn định, tính ngẫu nhiên.
Với giải thuật M-CSEA, so sánh kết quả thử nghiệm với giải thuật gốc CSEA thấy
rằng, M-CSEA sử dụng kỹ thuật chỉ dẫn với chiến lược lựa chọn số lượng cụm linh hoạt
khi lấy dữ liệu mẫu để huấn luyện, giải thuật đã tạo nên sự cân bằng tốt hơn giữa chất
lượng hội tụ và đa dạng. Cụ thể, ở những thế hệ đầu, giải thuật đạt kết quả tốt hơn với
các bài toán DTLZ1, DTLZ2, DTLZ3, DTLZ6, DTLZ8 trên GD và DTLZ1, DTLZ3,
DTLZ4, DTLZ6, DTLZ7, DTLZ8 trên IGD. Ở các thế hệ liền sau đó, M-CSEA đạt kết
quả tốt hơn với các bài toán DTLZ2, DTLZ3, DTLZ6, DTLZ7, DTLZ8 trên GD. Trên
IGD, giải thuật cũng tốt hơn với các bài toán DTLZ1, DTLZ3, DTLZ4, DTLZ6, DTLZ7,
DTLZ8. Ở các thế hệ cuối, M-CSEA đạt kết quả tốt hơn với các bài toán DTLZ1,
DTLZ2, DTLZ3, DTLZ5, DTLZ6, DTLZ7, DTLZ8 trên GD và DTLZ1, DTLZ2,
DTLZ3, DTLZ6, DTLZ7, DTLZ8 trên IGD.
Qua kết quả thử nghiệm cho thấy, việc đề xuất sử dụng kỹ thuật chỉ dẫn tự động với
chiến lược lựa chọn từ số cụm dữ liệu linh hoạt đã giúp nâng cao hiệu quả của giải thuật
tiến hóa đa mục tiêu sử dụng mô hình Kriging. Tương tự như M-K-RVEA, kết quả thử
nghiệm của M-CSEA đã minh chứng cho giả thuyết về tác động của tiến trình thời gian,
chất lượng hội tụ hiện tại của quần thể và đặc điểm của bài toán tới việc duy trì cân bằng
giữa khả năng thăm dò và khai thác để đảm bảo quần thể vừa có tính hội tụ, vừa đa dạng.
Và cũng cần phải điều chỉnh kịp thời tại các giai đoạn tiến hóa để duy trì sự cân bằng
giữa thăm dò và khai thác.
Đối với các giải thuật sử dụng kỹ thuật chỉ dẫn điều chỉnh tham số thông qua tương
tác, đặt tên là iK-RVEA và iCSEA tương ứng với các giải thuật gốc K-RVEA và CSEA,
sẽ có một bước tương tác với người dùng được thêm vào vòng lặp qua các thế hệ. Ở bước
tương tác này, giao diện hiển thị các thông tin tham chiếu như: giá trị hiện tại của các
tham số chung (số thế hệ, số lần đánh giá), tham số wmax, K (tương ứng của K-RVEA và
CSEA), biểu đồ thay đổi các độ đo GD, IGD từ thế hệ đầu đến hiện tại. Giao diện tương
tác cho phép người dùng nhập các giá trị mới của các tham số. Người dùng không nhất
thiết phải tương tác tại mỗi thế hệ mà chỉ tương tác khi muốn kiểm tra và xem xét để điều
chỉnh tham số. Trong các thử nghiệm, chúng tôi tiến hành tương tác 5 lần với mỗi giải
thuật và quan sát sự thay đổi của các độ đo GD, IGD cùng với các giai đoạn của quá trình
tiến hóa. Bằng kiến thức chuyên gia để điều chỉnh giá trị các tham số trong các giải thuật
Công nghệ thông tin
20 N. Đ. Định, N. Long, T. T. Kiên, “Kỹ thuật chỉ dẫn cho giải thuật mô hình đại diện.”
iK-RVEA và iCSEA, quá trình tiến hóa đã có những biến đổi tích cực, bổ sung đầy đủ
hơn cho kỹ thuật chỉ dẫn nhằm nâng cao hiệu quả giải thuật. Thật vậy, thông qua tương
tác, việc điều chỉnh các tham số quan trọng như thời điểm cập nhật mô hình, số lượng
mẫu các cụm dùng để phân lớp, giúp cho các giải thuật có chất lượng tốt hơn. Kết quả
của sự tương tác với người dùng chính là các yếu tố ảnh hưởng đến chất lượng của giải
thuật (số thế hệ đã trải qua, số lần đánh giá, tính hội tụ và đa dạng của quần thể hiện tại,
đặc điểm của các bài toán). Các kết quả của sự tương tác cùng với sự điều chỉnh tự động
tham số đã tạo nên kỹ thuật chỉ dẫn hiệu quả cho các giải thuật tiến hóa đa mục tiêu sử
dụng mô hình đại diện có ý nghĩa quan trọng đối với việc giải quyết các bài toán thực tế.
6. KẾT LUẬN
Giải các bài toán khó bằng giải thuật tiến hóa đa mục tiêu sử dụng mô hình đại diện là
lựa chọn hiệu quả, được các nhà nghiên cứu quan tâm. Đã có nhiều công bố giải quyết
hiệu quả các bài toán khó. Tuy nhiên, các chiến lược cập nhật mô hình đại diện, lựa chọn
dữ liệu mẫu để huấn luyện mô hình, vẫn còn chưa được đánh giá kỹ, nhất là sự ảnh
hưởng đến việc duy trì cân bằng giữa khả năng thăm dò và khai thác của quá trình tiến
hóa, cải thiện chất lượng hội tụ và đa dạng của quần thể, là hai yếu tố quan trọng quyết
định chất lượng của giải thuật. Trên cơ sở phân tích các điều kiện trong quá trình tiến
hóa, chúng tôi đã đề xuất kỹ thuật chỉ dẫn để có chiến lược cập nhật mô hình và lựa chọn
dữ liệu mẫu linh hoạt, hiệu quả hơn.
Kết quả thử nghiệm đã minh chứng cho giả thuyết và khẳng định tính hiệu quả của kỹ
thuật chỉ dẫn, nhất là sự kết hợp phương pháp tự động điều chỉnh tham số với điều chỉnh
tham số thông qua tương tác người dùng trong quá trình tiến hóa. Bài báo cũng đưa ra
khuyến nghị sử dụng để bảo đảm tính bền vững, kết quả hội tụ và đa dạng trong giải
quyết các bài toán đa mục tiêu khó trong thực tế.
TÀI LIỆU THAM KHẢO
[1]. Seongim Choi, Juan J Alonso, and Hyoung S Chung, "Design of a low-boom supersonic
business jet using evolutionary algorithms and an adaptive unstructured mesh method",
AIAA paper, 1758:2004, 2004.
[2]. Michael TM Emmerich, Kyriakos C Giannakoglou, Boris Naujoks, "Single-and
multiobjective evolutionary optimization assisted by Gaussian random field metamodels",
IEEE Transactions on Evolutionary Computation, 10(4):421-439, 2006.
[3]. Chariklia A Georgopoulou and Kyriakos C Giannakoglou, "Multi-objective metamodel-
assisted memetic algorithms", In Multi-Objective Memetic Algorithms, pages 153-181.
Springer, 2009.
[4]. Tushar Goel, Rajkumar Vaidyanathan, Raphael T Haftka, Wei Shyy, Nestor V Queipo,
and Kevin Tucker, "Response surface approximation of Pareto optimal front in multi-
objective optimization", Computer methods in applied mechanics and engineering, 196(4-
6):879-893, 2007.
[5]. Rolland L Hardy, "Multi-quadric equations of topography and other irregular surfaces",
Journal of geophysical research, 76(8):1905-1915, 1971.
[6]. Afzal Husain and Kwang-Yong Kim, "Enhanced multi-objective optimization of a micro-
channel heat sink through evolutionary algorithm coupled with multiple surrogate models",
Applied Thermal Engineering, 30(13):1683-1691, 2010.
[7]. Amitay Isaacs, Tapabrata Ray, and Warren Smith, "An evolutionary algorithm with
spatially distributed surrogates for multi-objective optimization", In Australian Conference
Nghiên cứu khoa học công nghệ
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 21
on Artificial Life, pages 257-268. Springer, 2007.
[8]. Xingtao Liao, Qing Li, Xujing Yang, Weigang Zhang, and Wei Li, "Multi-objective
optimization for crash safety design of vehicles using stepwise regression model",
Structural and multidisciplinary optimization, 35(6):561-569, 2008.
[9]. Saul Zapotecas Martinez and C. A Coello Coello, "A memetic algorithm with non gradient-
based local search assisted by a meta-model", In International Conference on Parallel
Problem, Solving from Nature, pages 576-585. Springer, 2010.
[10]. K. Miettinen, "Nonlinear multi-objective optimization", Kluwer Academic Publishers,
Boston, USA, 1999.
[11]. Alfredo Arias Montano, Carlos A Coello Coello, and Efren Mezura-Montes, "MODE-
LD+SS: A novel differential evolution algorithm incorporating local dominance and scalar
selection mechanisms for multi-objective optimization", In Evolutionary Computation
(CEC), 2010 IEEE Congress on, pages 1-8. IEEE, 2010.
[12]. Martin Pilát and Roman Neruda, "Lamm-mma: Multi-objective memetic algorithm with
local aggregate meta-model", In Proceedings of the 13th annual conference companion on
Genetic and evolutionary computation, pages 79-80. ACM, 2011.
[13]. Martin Pilat and Roman Neruda, "An evolutionary strategy for surrogate-based
multiobjective optimization", In Evolutionary Computation (CEC), 2012 IEEE Congress
on, pages 1-7. IEEE, 2012.
[14]. Martin Piláat and Roman Neruda, "Aggregate meta-models for evolutionary multi-objective
and many-objective optimization", Neurocomputing, 116:392-402, 2013.
[15]. D. C. Montgomery R. H. Myers and C. M. Anderson-Cook, "Response surface
methodology: Process and product optimization using designed experiments", Wiley New
York, 2009.
[16]. Vladimir Vapnik, "Statistical learning theory. 1998, volume 3", Wiley, New York, 1998.
[17]. Ivan Voutchkov and AJ Keane, "Multi-objective optimization using surrogates", 2006.
[18]. Saul Zapotecas Martinez and Carlos A Coello Coello, "MOEA/D assisted by RBF networks
for expensive multi-objective optimization problems", In Proceedings of the 15th annual
conference on Genetic and evolutionary computation, pages 1405-1412. ACM, 2013.
[19]. D.A.V. Veldhuizen, "Multi-objective evolutionary algorithms: Classifications, analyses, and
new innovation", PhD thesis, Department of Electrical Engineering and Computer
Engineering, Airforce Institue of Technology, Ohio, 1999.
[20]. Linqiang Pan, Cheng He, Ye Tian, Handing Wang, Xingyi Zhang, and Yaochu Jin, "A
classification-based surrogate-assisted evolutionary algorithm for expensive many-objective
optimization", IEEE Transactions on Evolutionary Computation, 23(1):74-88, 2018.
[21]. Ran Cheng, Yaochu Jin, Markus Olhofer, and Bernhard Sendhoff, "A reference vector
guided evolutionary algorithm for many-objective optimization", 20(5):773-791, 2016.
[22]. T Chugh, Y Jin, K Miettinen, J Hakanen, and K Sindhya, "K-RVEA: A Kriging-assisted
evolutionary algorithm for many-objective optimization", Scientific Computing no.B, 2, 2016.
[23]. Kalyanmoy Deb, Lothar Thiele, Macro Laumanns, Eckart Zitzler, "Scalable test problems
for evolutionary multi-objective optimization", In: Evolutionary multiobjective
optimization, Springer, London, 2005. p. 105-145.
[24]. A. Diaz-Manriquez, G. Toscano, J. Barron-Zambrano, E. Tello-Leal, "A review of
surrogate assisted multi-objective evolutionary algorithms", Computational Intelligence
and Neuroscience Volume 2016, Hindawi.
[25]. I. Voutchkov, A. Keane, "Multi-objective optimization using surrogates", Computational
Intelligence in Optimization, ALO 7, pp. 155-175, 2010.
[26]. Hussein, Rayan, and Kalyanmoy Deb, "A generative kriging surrogate model for
constrained and unconstrained multi-objective optimization", Proceedings of the Genetic
Công nghệ thông tin
22 N. Đ. Định, N. Long, T. T. Kiên, “Kỹ thuật chỉ dẫn cho giải thuật mô hình đại diện.”
and Evolutionary Computation Conference 2016.
[27]. Dammak, Khalil, and Abdelkhalak El Hami. "Multi-objective reliability based design
optimization using Kriging surrogate model for cementless hip prosthesis", Computer
Methods in Biomechanics and Biomedical Engineering (2020): 1-14.
ABSTRACT
GUIDANCE TECHNIQUES FOR SURROGATE ASSISTED MULTI-OBJECTIVE
EVOLUTIONARY ALGORITHMS
Solving difficult and high cost problems (expensive problems) by using surrogate
model in multi-objective evolutionary algorithm is an effective choice and is interested by
many researchers. Algorithms have been published that effectively solve expensive
problems. However, the strategy in updating the surrogate model, selecting sample data to
train the model, etc. has not been thoroughly evaluated, especially affecting the ability to
keep the balance of exploration and exploitation. Quality of convergence and diversity,
they are important factors determine the quality of a multi-objective optimization
algorithm. On the basis of analyzing the conditions in the search process, the guidance
technique based on the assessed value at different times to have a strategy for updating the
model and selecting sample data more flexible and efficient has been proposed.
Through the test results, the comparation, it has demonstrated the explanation and
affirmed the effectiveness of guidance techniques, especially combining automatic guide
and user interaction in the search process. The publication also recommends using to
create sustainability, convergence and diversity results in solving expensive problems in
the real world.
Keywords: Guidance technique; Surrogate model; Kriging; MOEAs.
Nhận bài ngày 30 tháng 09 năm 2020
Hoàn thiện ngày 10 tháng 12 năm 2020
Chấp nhận đăng ngày 15 tháng 12 năm 2020
Địa chỉ: 1Viện Công nghệ thông tin/Viện KH-CN quân sự;
2Khoa Chỉ huy tham mưu/Học viện Quốc phòng.
*Email: nddinh76@gmail.com.
File đính kèm:
 ky_thuat_chi_dan_cho_giai_thuat_tien_hoa_da_muc_tieu_su_dung.pdf
ky_thuat_chi_dan_cho_giai_thuat_tien_hoa_da_muc_tieu_su_dung.pdf

