Khảo sát thông số chuyển vị từ tín hiệu cảm biến đo gia tốc kết cấu dầm nhịp giản đơn

TAÏP CHÍ PHAÙT TRIEÅN KH&CN, TAÄP 18, SOÁ K8- 2015 
 Trang 111 
Khảo sát thông số chuyển vị từ tín hiệu cảm 
biến đo gia tốc kết cấu dầm nhịp giản đơn 
 Nguyễn Công Đức 
 Trần Văn Một 
 Phan Công Bàn 
 Dương Lê Trường 
Trường Đại học Xây dựng Miền Trung, Thành phố Tuy Hòa, Tỉnh Phú Yên 
TÓM TẮT 
Nghiên cứu này trình bày phương pháp 
phân tích tín hiệu từ cảm biến đo gia tốc dao 
động kết cấu công trình xây dựng có nhịp 
giản đơn để thu được thông số chuyển vị 
phục vụ cho công tác đánh giá khả năng chịu 
tải trọng của công trình. Phương pháp tích 
phân số tín hiệu cảm biến đo gia tốc dao 
động kết hợp sử dụng các bộ lọc thông thấp 
và thông cao, ứng dụng kỹ thuật wavelet 
trong xử lý nhiễu của tín hiệu và nén dữ liệu 
từ các cảm biến đo chuyên dùng. Phương 
pháp đạo hàm số tín hiệu cảm biến đo 
chuyển vị loại biến áp vi sai biến đổi tuyến 
tính (LVDT) để dự đoán đáp ứng dao động 
kết cấu công trình. Phương pháp thực 
nghiệm đo thông số dao động và chuyển vị 
trên dầm liên kết giản đơn, số liệu thực 
nghiệm đo trên kết cấu công trình xây dựng 
thực tế chịu tác dụng tải trọng động được 
dùng để phân tích. 
Từ khóa: Đo dao động; Phân tích phổ tần số dao động, Cảm biến đo gia tốc dao động, 
Cảm biến đo chuyển vị LVDT, tích phân số tín hiệu cảm biến gia tốc, đạo hàm số tín hiệu chuyển 
vị. 
1. ĐẶT VẤN ĐỀ 
Trong những năm gần đây, việc đánh giá 
kiểm định kết cấu công trình xây dựng mới, 
chuẩn đoán và giám sát các hư hỏng và vết nứt 
của những kết cấu công trình xây dựng cũ tương 
đối phổ biến ở nước ta. Các thông số đo đạc như 
biến dạng, chuyển vị và dao động tích hợp trong 
các thiết bị điện tử có kết nối với máy tính thông 
qua phần mềm xử lý rất linh hoạt. Nguyên lý đo 
biến dạng bề mặt của kết cấu bê tông cốt thép, kết 
cấu thép tương đối đơn giản là chỉ việc dán các lá 
đo điện trở phù hợp lên các bề mặt cần đo hay sử 
dụng các bộ chuyển đổi đo biến dạng khác. 
Tương tự đối với thông số dao động ta có thể sử 
dụng cảm biến đo gia tốc dao động gắn trên bề 
mặt kết cấu cần đo bằng cách sử dụng keo dán 
chuyên dùng. 
Tuy nhiên với thông số chuyển vị phức tạp 
hơn nhiều, để sử dụng loại cảm biến đo chuyển 
vị loại biến áp vi sai biến đổi tuyến tính (Linear 
Variable Displacement Transducer viết tắt là 
LVDT) cần phải chuẩn bị một điểm tựa cố định 
và chắc chắn. Vấn đề này chỉ có thể thực hiện 
trong một vài trường hợp như: kết cấu nhịp cầu 
trên bờ (điểm tựa cố định là mặt đất), kết cấu 
móng cọc công trình (điểm tựa cũng là mặt đất). 
Khi kết cấu công trình vượt nhịp lớn nằm trên 
những địa hình mà việc lắp đặt hệ dàn giáo khó 
khăn để phục vụ công tác kiểm định thử tải. Kết 
cấu nhịp cầu vượt sông chỉ có thể lắp đặt hệ dàn 
SCIENCE & TECHNOLOGY DEVELOPMENT, Vol 18, No.K8- 2015 
Page 112 
giáo treo và hầu như khó có thể tìm được một 
điểm tựa cố định để khảo sát thông số chuyển vị 
của kết cấu dưới tác dụng tải trọng tĩnh và động. 
(a) 
(b) 
(b) 
Hình 1. Các cảm biến đo dao động và chuyển vị gắn 
trên kết cấu công trình cầu nhịp gần bờ và nhịp giữa 
song (a) Cầu Hùng Vương, Phú Yên; (b) Cầu Ông 
Cộ, Bình Dương 
Công tác lắp dựng hệ dàn giáo cho toàn bộ 
không gian bên dưới nhịp cầu trên bờ để gắn các 
cảm biến đo biến dạng, chuyển vị và dao động 
một nhịp gần bờ (Cầu Hùng Vương, Phú Yên) 
trên hình 1.a, tùy theo số điểm đo (biến dạng, 
chuyển vị và dao động) và số lượng dầm trên một 
nhịp có thể bố trí số lượng dàn giáo cho phù hợp. 
Công việc này tương đối phức tạp và gây tốn kém 
không cần thiết khi thực hiện công tác kiểm định. 
Số lượng điểm đo càng nhiều mức độ đánh giá 
càng chính xác và mức độ tin cậy càng cao. 
Tuy nhiên, công tác thử tải đối với nhịp nằm 
ở giữa sông đôi khi nằm trên cao việc tìm điểm 
cố định lắp hệ dàn giáo tương đối khó khăn và 
ảnh hưởng đến tiến độ thử tải. Phương án thay thế 
là lắp hệ dàn giáo treo để gắn cảm biến đo biến 
dạng và đo dao động một nhịp giữa sông (Cầu 
Ông Cộ, Bình Dương) trên hình 1.b. Điểm cố 
định trong trường hợp này chỉ có thể là 2 trụ của 
nhịp thử tải, nếu đặt vấn đề là sử dụng 2 điểm tựa 
cố định này để gắn cảm biến LVDT đo chuyển vị 
thì mức độ chính xác của số liệu đo, có thể nói 
rằng không đáng tin cậy vì mố và trục cũng có 
chuyển vị đứng, ngang và dọc. Công tác đánh giá 
thử tải, kiểm định công trình cầu gần như cũng 
phải khảo sát các thông số biến dạng, chuyển vị 
và dao động mố trụ cầu. 
Một số giải pháp thay thế để khắc phục vấn 
đề khó khăn này, tùy thuộc vào phương án thử 
tải, hình dạng kết cấu cũng như vị trí của kết cấu 
công trình có thể sử dụng các loại thiết bị khác 
như: sử dụng cảm biến lazer, máy kinh vĩ, máy 
toàn đạc. Các loại thiết bị này cũng có một hạn 
chế nhất định đó là mức độ chính xác, sai số, tính 
linh động chưa cao nên việc sử dụng cho công tác 
kiểm định thử tải chưa nhiều. 
Nghiên cứu này đề xuất phương pháp sử 
dụng dữ liệu cảm biến đo gia tốc dao động để vừa 
có thể phân tích thông số chuyển vị và vừa phâ ... c chủ 
yếu về vấn đề phân tích phổ tần số của cảm biến 
đo gia tốc dao động, từ đó tính tần số dao động 
riêng và cưỡng bức. Thông số chuyển vị thu được 
từ cảm biến đo chuyển vị LVDT khá phổ biến 
trong công tác kiểm định kết cấu công trình cầu 
theo tiêu chuẩn 22TCN 243:1998. Thí nghiệm 
thử động biến dạng lớn (Pile Driving Analyzer 
viết tắt là PDA) cho các loại cọc. Thiết bị PDA 
này sử dụng cảm biến đo gia tốc dao động để tính 
toán vận tốc và chuyển vị dựa trên thuật toán 
wavelet, từ đó đánh giá chất lượng cọc và khả 
năng chịu tải trọng theo tiêu chuẩn ASTM 
D4945-08 và TCVN 9395:2012. 
2. PHƯƠNG PHÁP TÍCH PHÂN SỐ TÍN 
HIỆU CẢM BIẾN GIA TỐC 
a. Phương pháp tích phân số dữ liệu gia tốc 
dựa vào thuật toán Trapezoidal 
Giả sử hàm tín hiệu gia tốc là một hàm theo 
thời gian, khi đó chúng ta có mối liên hệ giữa 
chuyển vị ( )x t , vận tốc ( )v t , gia tốc ( )a t được 
biểu diễn dưới dạng mối quan hệ giữa chuyển vị 
và gia tốc như sau: 
2 2
1 1
( ) ( ) 
t t t t
t t t t
x t a t dt dt
 (1) 
Tuy nhiên dữ liệu tín hiệu trong nghiên cứu 
này là một tập dữ liệu rời rạc với N mẫu dữ liệu 
đo nên việc tích phân số cần rời rạc hóa như sau, 
[3]: 
 11 1. ;2
 1,2,3,...,
i i
i i i i
a a
v v t t
i N
 (2) 
Tương tự như vậy khi tích phân rời rạc dữ 
liệu tín hiệu vận tốc thành đáp ứng chuyển vị, [3]: 
 11 1 ;2
 1,2,3,...,
i i
i i i i
v v
x x t t
i N
 (3) 
b. Phương pháp tích phân số tín hiệu gia tốc 
dựa vào phép biến đổi FFT 
Giả thiết tín hiệu của cảm biến đo gia tốc dao 
động là một hàm theo thời gian khi đó ta có mối 
liện hệ giữa gia tốc, vận tốc và chuyển vị theo 
phân tích tần số (FFT) như sau: 
Hàm chuyển vị : 
2( ) ( ) iftx t X f e df 
 (4) 
Hàm vận tốc: 
2( ) ( ) ( ) iftv t x t X f e df 
  (5) 
Hàm gia tốc: 
2( ) ( ) ( ) ifta t x t X f e df 
  (6) 
Từ (4) và (5), thiết lập mối liên hệ giữa 
chuyển vị là nguyên hàm bậc hai của gia tốc: 
SCIENCE & TECHNOLOGY DEVELOPMENT, Vol 18, No.K8- 2015 
Page 114 
2
2
2
( ) ( )
 ( ) 
 ( ) 
 2 ( ) 
ift
ift
ift
dx t x t
dt
d X f e df
dt
dX f e df
dt
dif X f e df
dt
 



(7) 
Đối chiếu (7) với (6), ta có: 
( ) 2 ( )X f if X f   
Hay: 
( ) ( )( )
2
X f X fX f
if i 
  (8) 
trong đó: f là dải tần số (Hz) của tín hiệu 
mở rộng từ 0f đến f ; f  2 - 
tần số )/( srad ; )( fX là biến đổi Fourier 
của hàm )(tx . 
c. Phương pháp biến đổi wavelet trong xử lý 
nhiễu tín hiệu 
Biến đổi wavelet thuận hàm liên tục, [9]: 
1( , ) ( ) 
 {0}, 
R
t bC a b s t dt
aa
a R b R

 (9) 
trong đó: ( , )C a b là các hệ số biến đổi 
wavelet liên tục; (t)s là hàm tín hiệu liên tục 
theo thời gian t (tín hiệu gia tốc hay tín hiệu 
chuyển vị);  là hàm phân tích wavelet; a là hệ 
số co dãn; b là hệ số dịch chuyển. 
Biến đổi wavelet thuận dữ liệu rời rạc, [9]: 
2
1( , ) ( ) 
 2 , 2 , ( , )
R
j j
t bC a b s t dt
aa
a b k j k Z

 (10) 
trong đó: ( , )C a b là các hệ số biến đổi 
wavelet rời rạc; (t)s là hàm tín hiệu dữ liệu rời 
rạc theo thời gian t (dữ liệu tín hiệu gia tốc hay 
tín hiệu chuyển vị);  là hàm phân tích wavelet. 
Biến đổi wavelet ngược hàm liên tục , [9]: 
2
1 1 db( ) ( , )
RR
t b das t C a b
K a aa

(11) 
với K là hệ số phụ thuộc vào hàm phân tích 
wavelet  . 
Biến đổi wavelet ngược hàm rời rạc, [9]: 
,( ) ( , ) ( )j k
j Z k Z
s t C j k t
   (12) 
d. Quy trình tích phân số tín hiệu cảm biến 
đo gia tốc dao động và vi phân số tín hiệu cảm 
biến đo chuyển vị 
Quy trình sử dụng thuật toán biến đổi 
wavelet rời rạc thuận cho tín hiệu cảm biến đo gia 
tốc dao động và tín hiệu cảm biến đo chuyển vị, 
từ đây tích phân số tín hiệu gia tốc hình 2.a và vi 
phân số tín hiệu chuyển vị hình 2.b. Tín hiệu cảm 
biến đo gia tốc dao động và tín hiệu gia tốc từ 
việc vi phân số tín hiệu đo chuyển vị LVDT sẽ 
được phân tích phổ tần số để kiểm tra kết quả tần 
số dao động riêng và dao động cưỡng bức từ đó 
kiểm tra mức độ hội tụ kết quả, làm cơ sở cho 
việc đánh giá phép tích phân cũng như vi phân 
số. 
Nghiên cứu này phân tích dữ liệu từ cảm 
biến đo gia tốc dao động và cảm biến đo chuyển 
vị LVDT thực nghiệm. Nhóm nghiên cứu sử 
dụng họ wavelet là Daubechies (db), một số họ 
wavelet khác cũng cho kết quả tương đối hiệu 
quả, tuy nhiên họ “db” cho kết quả khả quan hơn 
khi xét về mặt biên độ chuyển vị, biên độ dao 
động và ứng xử cơ học khi kết cấu chịu tác dụng 
của tải trọng di động. 
TAÏP CHÍ PHAÙT TRIEÅN KH&CN, TAÄP 18, SOÁ K8- 2015 
 Trang 115 
(a) 
(b) 
Hình 2. Biến đổi wavelet rời rạc tín hiệu cảm biến đo gia tốc và tính hiệu cảm biến đo chuyển vị. 
(a) Tích phân số tín hiệu gia tốc thành chuyển vị; (b) Vi phân số tín hiệu chuyển vị thành gia tốc; 
cA là viết tắt của từ “approximation coefficients” là thành phần xấp xỉ; cD là viết tắt của từ “details coefficients” 
là thành phần chi tiết. 
3. PHÂN TÍCH KẾT QUẢ THỰC NGHIỆM 
(a) 
(b) 
Hình 3. Mô hình thí nghiệm gắn cảm biến đo chuyển vị và đo gia tốc dao động 
(a) Các thiết bị đo sử dụng trong thí nghiệm; (b) Mô hình dầm thép tựa đơn 2 đầu chịu tác dụng tải trọng di 
chuyển (l=1320mm; m=2kg; h=13mm, b=27mm ,t=2mm, v=100mm/s; g=9.81m/s2). Các thiết bị thí nghiệm 
gồm: (1) Bộ thiết bị thu và phát tín hiệu đo truyền vào máy tính; (2) Cảm biến đo gia tốc dao động; (3) Động 
cơ kéo tải trọng di động công suất nhỏ; (4) Cảm biến đo chuyển vị LVDT; (5) Bộ chất tải di động được kéo 
nhờ động cơ; (6) Hệ gối tựa cố định; (7) Dầm thép trong thí nghiệm. 
Tích phaân soá
Tín hieäu
chuyeån vò (cA)
Tín hieäu
chuyeån vò (cD)
Tích phaân soá
Tích phaân soáTích phaân soá
Bieán ñoåi
wavelet rôøi
raïc thuaän
Tín hieäu
gia toác
Boä loïc
thoâng thaáp
Boä loïc
thoâng cao
Tín hieäu
gia toác (cA)
Tín hieäu
gia toác (cD)
Tín hieäu
vaän toác (cA)
Tín hieäu
vaän toác (cD)
Tín hieäu
chuyeån vò
Boä loïc
thoâng thaáp
Boä loïc
thoâng cao
Tín hieäu
chuyeån vò(cA)
Tín hieäu
chuyeån vò(cD)
Tín hieäu
vaän toác (cA)
Tín hieäu
vaän toác (cD)
Vi phaân soá
Tín hieäu
gia toác (cA)
Tín hieäu
gia toác (cD)
Vi phaân soá
Vi phaân soáVi phaân soá
Bieán ñoåi
wavelet rôøi
raïc thuaän
l
m=G/g
l/2
l/4
v
h
b
t
A2
27
2
LV
98
04
A2
26
7
LV
35
52
SCIENCE & TECHNOLOGY DEVELOPMENT, Vol 18, No.K8- 2015 
Page 116 
Thí nghiệm dầm liên kết giản đơn chịu tải 
trọng di động sử dụng các cảm biến đo chuyển vị 
(mã số cảm biến: LV9804 và LV3552); cảm biến 
đo gia tốc dao động (mã số cảm biến A2272 và 
A2267) gắn ở vị trí giữa nhịp ứng với dao động 
của dạng dao động riêng thứ 1, và gắn ở vị trí 1/4 
nhịp ứng với dao động của dạng dao động riêng 
thứ 2. Hệ thống thiết bị thu nhận tín hiệu STS-
WiFi (của hãng BDI, Mỹ) và phần mềm thu nhận 
tín hiệu đo WinSTS3 (Phòng Thí nghiệm chuyên 
ngành xây dựng, Trường ĐHXD Miền Trung: 
LAS-XD 162) được sử dụng để tiến hành thí 
nghiệm đo trên hình 3.a và mô hình dầm gắn các 
cảm biến đo tại các vị trí trên hình 3.b. 
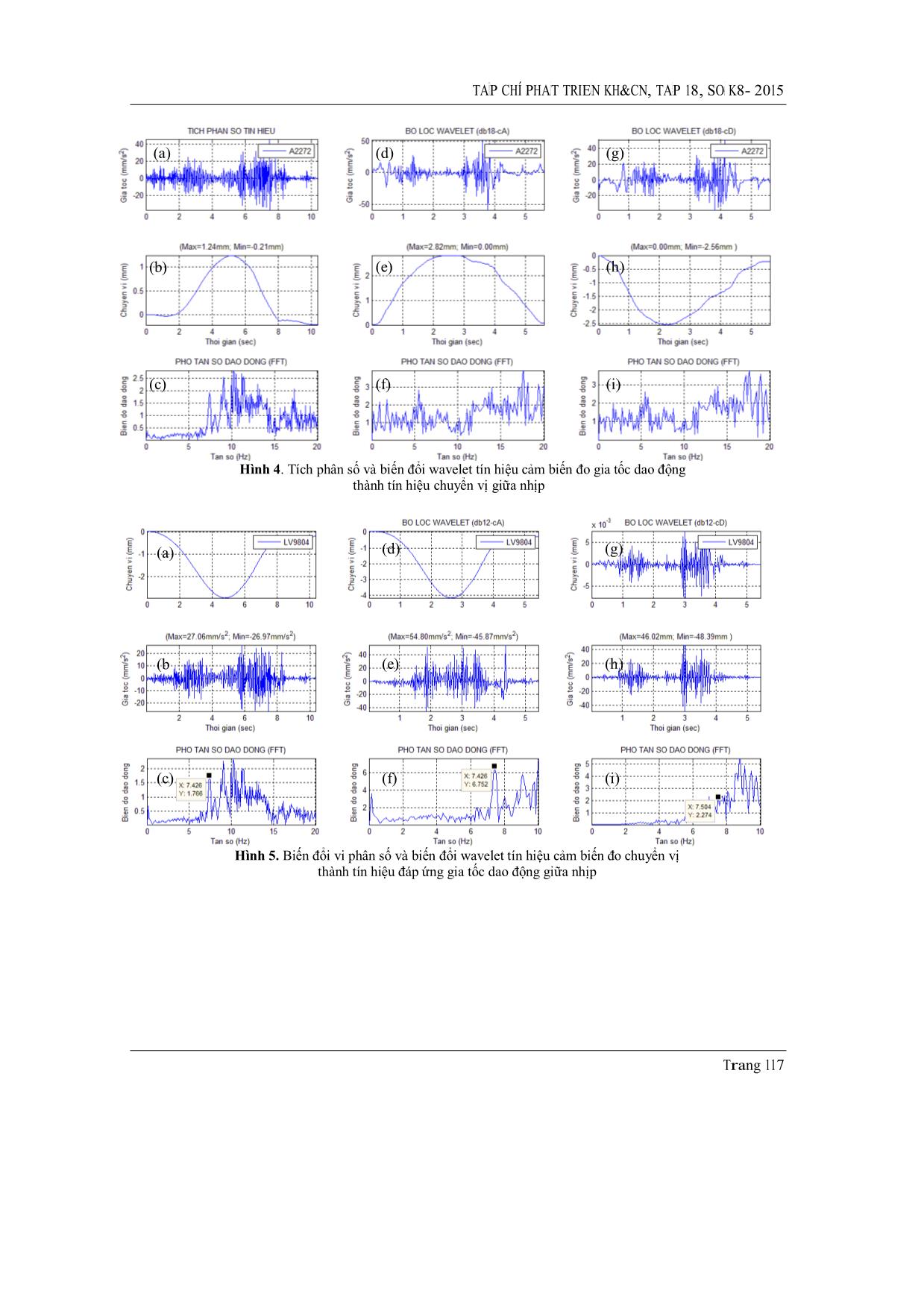
Đồ thị tín hiệu từ cảm biến đo gia tốc dao 
động A2272 hình 4.a. Phương pháp tích phân số 
tín hiệu cảm biến đo gia tốc theo quy trình thông 
thường với chuyển vị và vận tốc ban đầu bằng 
không trên hình 4.b với giá trị biên độ là 1.24mm. 
Hình 4.d và 4.e là kết quả từ việc lọc tín hiệu bằng 
cách sử dụng biến đổi wavelet họ db18 với hệ số 
cA, biên độ chuyển vị sau khi phân tích là 
2.82mm. Phân tích wavelet họ db18 với hệ số cD 
của tín hiệu cảm biến đo gia tốc này có biên độ 
chuyển vị là -2.56mm trên hình 4.h, với kết quả 
này có thể nhận xét về mặt trực quan ứng xử kết 
cấu dưới tác dụng của tải trọng động và so sánh 
với kết quả thực nghiệm từ cảm biến đo chuyển 
vị LV9804 là -2.94mm. Các hình 4.c, 4.f và 4.i là 
các đồ thị phân tích phổ tần số dao động cưỡng 
bức và dao động riêng tương ứng với các đồ thị 
tín hiệu đo gia tốc ở các cột tương ứng. 
Kết quả phân tích wavelet đã lọc bỏ những 
dải tần số nhiễu do nhiều nguyên nhân như: gối 
tựa, ma sát giữa xe tạo tải trọng động và dầm khi 
xe chạy. Đồ thị của cảm biến đo chuyển vị thực 
nghiệm và đồ thị tín hiệu chuyển vị từ việc biến 
đổi wavelet và tích phân số cho thấy kết quả 
tương đối tin cậy về mặt ứng xử cơ học khi dầm 
thép nhịp giản đơn chịu tác dụng tải trọng di 
động. Nghiên cứu này đã sử dụng nhiều bộ lọc 
khác nhau như: bộ lọc thông thấp, bộ lọc thông 
cao, bộ lọc dải tần số, và một số bộ lọc phổ biến 
khác để loại bỏ nhiễu nhưng không hiệu quả. 
Biến đổi wavelet thực hiện đối với tín hiệu cảm 
biến đo gia tốc cho kết quả tương đối khả quan và 
có nhiều tiềm năng ứng dụng đối với vấn đề 
nghiên cứu này. Kết quả phân tích wavelet họ db 
có khả năng ứng dụng cho vấn đề này, chủ yếu 
với họ từ db10 trở lên, với họ db thấp khả năng 
phân tích kết quả còn nhiều hạn chế. 
Hình 5.a là đồ thị tín hiệu cảm biến đo 
chuyển vị LV9804. Biến đổi tín hiệu đo chuyển 
vị này được kết quả hình 5.d và thực hiện phép vi 
phân số tín hiệu của cảm biến đo chuyển vị thành 
thành tín hiệu đo gia tốc dao động. Đồ thị này có 
biên độ lớn nhất +54.80mm/s2 và nhỏ nhất là -
45.87mm/s2, trên hình 5.e và hình 5.f là kết quả 
phân tích phổ tần số dao động. Đồ thị hình 5.g là 
phân tích nhiễu tín hiệu của cảm biến đo chuyển 
vị và đồ thị phân tích phổ tần số tín hiệu này trên 
hình 5.i. Biến đổi wavelet với họ db12 với các hệ 
số cA cho kết quả về biên dộ dao động so với kết 
quả thực nghiệm từ cảm biến đo gia tốc A2272 
trên hình 4.a. 
TAÏP CHÍ PHAÙT TRIEÅN KH&CN, TAÄP 18, SOÁ K8- 2015 
 Trang 117 
Hình 4. Tích phân số và biến đổi wavelet tín hiệu cảm biến đo gia tốc dao động 
thành tín hiệu chuyển vị giữa nhịp 
Hình 5. Biến đổi vi phân số và biến đổi wavelet tín hiệu cảm biến đo chuyển vị 
thành tín hiệu đáp ứng gia tốc dao động giữa nhịp 
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
(a) 
(b
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
SCIENCE & TECHNOLOGY DEVELOPMENT, Vol 18, No.K8- 2015 
Page 118 
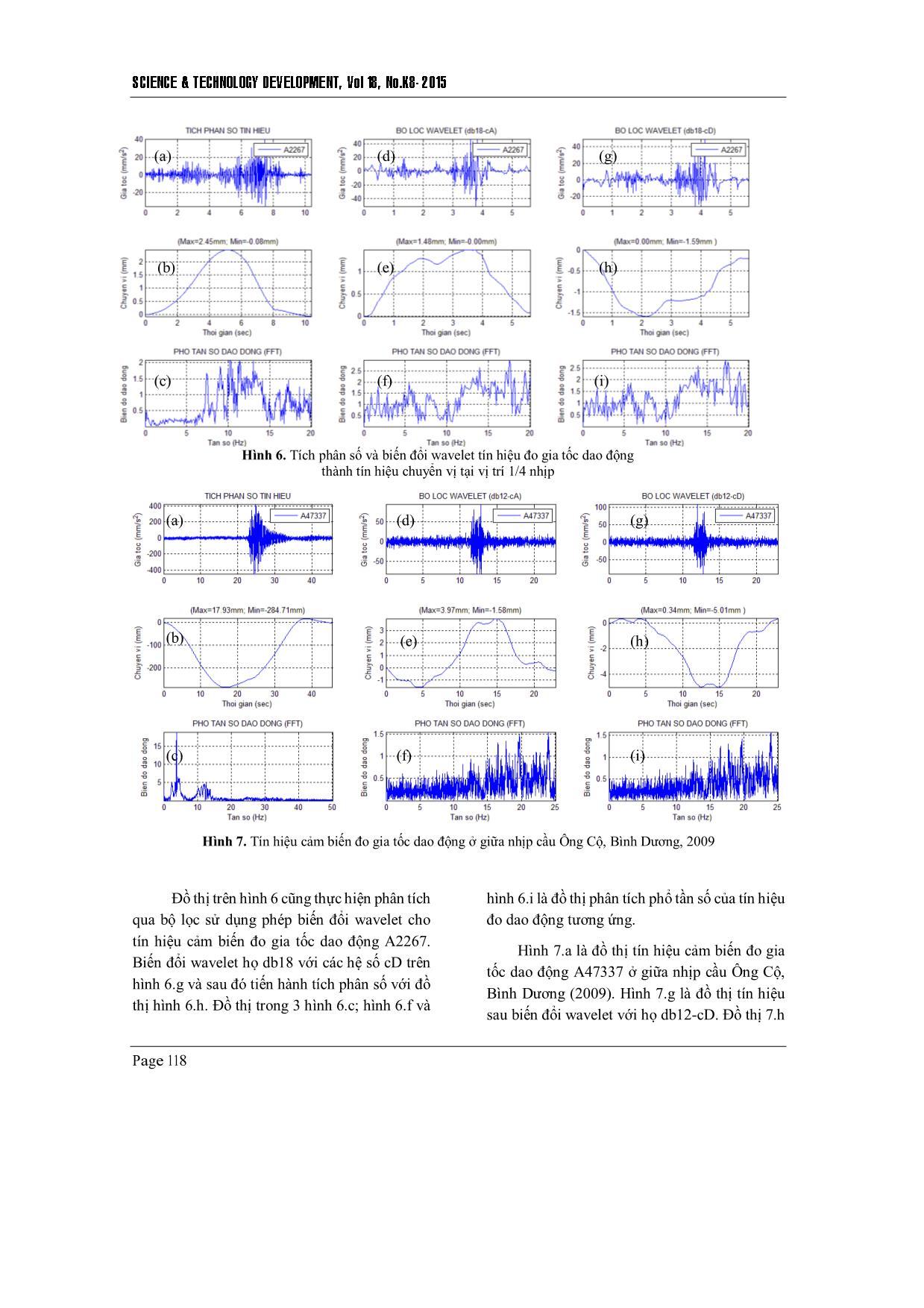
Hình 6. Tích phân số và biến đổi wavelet tín hiệu đo gia tốc dao động 
thành tín hiệu chuyển vị tại vị trí 1/4 nhịp 
Hình 7. Tín hiệu cảm biến đo gia tốc dao động ở giữa nhịp cầu Ông Cộ, Bình Dương, 2009 
 Đồ thị trên hình 6 cũng thực hiện phân tích 
qua bộ lọc sử dụng phép biến đổi wavelet cho 
tín hiệu cảm biến đo gia tốc dao động A2267. 
Biến đổi wavelet họ db18 với các hệ số cD trên 
hình 6.g và sau đó tiến hành tích phân số với đồ 
thị hình 6.h. Đồ thị trong 3 hình 6.c; hình 6.f và 
hình 6.i là đồ thị phân tích phổ tần số của tín hiệu 
đo dao động tương ứng. 
Hình 7.a là đồ thị tín hiệu cảm biến đo gia 
tốc dao động A47337 ở giữa nhịp cầu Ông Cộ, 
Bình Dương (2009). Hình 7.g là đồ thị tín hiệu 
sau biến đổi wavelet với họ db12-cD. Đồ thị 7.h 
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
(h) 
(i) 
TAÏP CHÍ PHAÙT TRIEÅN KH&CN, TAÄP 18, SOÁ K8- 2015 
 Trang 119 
là kết quả sau khi tích phân số tín hiệu cảm biến 
đo dao động thành tín hiệu chuyển vị, kết quả 
chuyển vị là -5.01mm. 
4. KẾT LUẬN 
Phương pháp phân tích wavelet và xử lý 
tích phân số tín hiệu từ cảm biến đo gia tốc dao 
động để từ đó phân tích thông số chuyển vị 
thông qua bộ hiệu chỉnh này. Đây là một thông 
số quan trọng trong việc đánh giá khả năng chịu 
tải của kết cấu công trình. Kết quả từ việc đo 
thông số chuyển vị và dao động sử dụng các loại 
cảm biến chuyên dùng qua đó làm cơ sở so sánh 
và phân tích. Phương pháp thực nghiệm của mô 
hình đã trình bày và từ đồ thị tín hiệu đo theo 
thời gian cho thấy việc phân tích tín hiệu chuyển 
vị từ tín hiệu cảm biến đo gia tốc dao động là 
hoàn toàn khả thi và có thể thực hiện được. Tuy 
nhiên không phải loại tải trọng động nào hay bất 
kỳ phương pháp thử động nào cũng có thể thực 
hiện công việc này thành công, nghiên cứu chỉ 
thực hiện trong không gian hẹp đó là các tải 
trọng động di chuyển trên kết cấu nhịp giản đơn 
có thể dầm thép hoặc dầm bê tông cốt thép dự 
ứng lực. Tải trọng tác dụng này có thể kiểm soát 
chứ không phải là tải trọng ngẫu nhiên, và vận 
tốc của tải trọng di động là luôn luôn không đổi 
trong suốt quá trình chạy trên kết cấu dầm mô 
hình cần thử nghiệm. Nghiên cứu tiếp tục triển 
khai cho các vấn đề như tải trọng động ngẫu 
nhiên và các loại kết cấu khác nhau sẽ được thí 
nghiệm trong những nghiên cứu tiếp theo. 
An experimental investigation of the 
displacement response on acceleration 
signal of single-span steel beam 
 Nguyen Cong Duc 
 Tran Van Mot 
 Phan Cong Ban 
 Duong Le Truong 
MienTrung University of Civil Engineering 
ABSTRACT 
The displacement responses can be 
obtained by numerical double intergration of 
accelerometer sensors which are used to 
measure vibration of the single-span steel 
beam. Application of wavelet transform to 
analyze acceleration and displacement 
signals, in which the beam is subjected to 
live-load. In the research, the results from 
the experimental displacements are 
presented and compared to the estimated 
displacements. 
Keywords: displacement sensor, accelerometer, vibration analysis, fast fourier transform, 
wavelet transform, frequency spectrum. 
SCIENCE & TECHNOLOGY DEVELOPMENT, Vol 18, No.K8- 2015 
Page 120 
TÀI LIỆU THAM KHẢO 
[1]. D.M. Boore, Effect of baseline corrections 
on displacements and response spectra for 
several recordings of the 1999 Chi-Chi, 
Taiwan, earthquake, Bulletin of the 
Seismological Society of America 91 (2001) 
1199–1211. 
[2]. Sangbo Han ,Retrieving the time history of 
displacement from measured acceleration 
signal, KSME International Journal, 
Volume 17, Issue 2 , pp 197-206 (2003). 
[3]. Ki-Tae Park, Sang-Hyo Kim, Heung-Suk 
Park, Kyu-Wan Lee. The Determination of 
Bridge Displayment Using Measured 
Acceleration, Engineering Structures 27 
(2005) 371-378. 
[4]. X. Meng, A.H. Dodson, G.W. Roberts. 
Detecting Bridge Dynamics with GPS and 
Triaxial Accelerometers, Engineering 
Structures 29 (2007) 3178-3184. 
[5]. Yoshimi OHTA , Omer AYDAN. An 
Integration Technique for Ground 
Displayment from Acceleration Records 
and its Application to Actual Earthquake 
Records, Journal of The School of Marine 
Science and Technology, Tokai Univesity, 
Vol5, No2, pp.1-12, 2007. 
[6]. Jin-Hak Yi, Soojin Cho, Ki-young Koo, 
Chung-Nang Yun, Jeong-Tae Kim, Chang-
Geun Lee, Won-Tae Lee. Bridge using 
Ambient Acceleration Measurements, 
Smart Structures and System, Vol.3, No.3 
(2007) 281-298. 
[7]. M. Gindy, R. Vaccaro, H.A. Nassif, State-
space approach for deriving bridge 
displacement from acceleration, Computer-
Aided Civil and Infrastructure Engineering 
23 (2008) 281–290 
[8]. Junhee Kim , Kiyoung Kim, Hoon Sohn, 
Autonomous dynamic displacement 
estimation from data fusion of acceleration 
and intermittent displacement 
measurements, Mechanical Systems and 
Signal Processing 42 (2014) 194–205. 
[9]. Daubechies, I., Ten lectures on wavelets, 
CBMS-NSF conference series in applied 
mathematics. SIAM Ed (1992).