Khảo sát động lực học hệ robot - Vũ khí trên cơ sở cơ học hệ nhiều vật

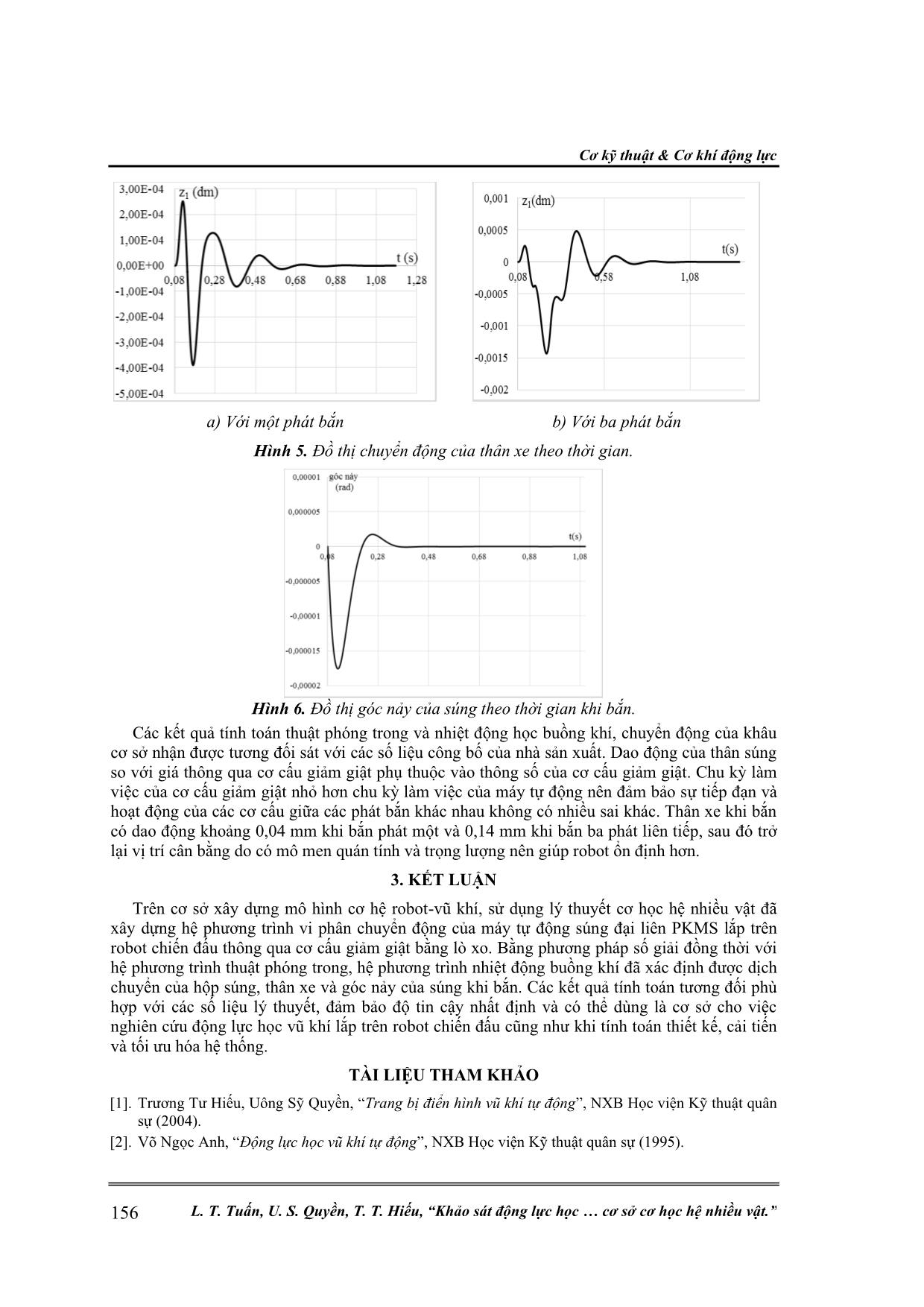
Cơ kỹ thuật & Cơ khí động lực 
 150 L. T. Tuấn, U. S. Quyền, T. T. Hiếu, “Khảo sát động lực học  cơ sở cơ học hệ nhiều vật.” 
KHẢO SÁT ĐỘNG LỰC HỌC HỆ ROBOT-VŨ KHÍ 
TRÊN CƠ SỞ CƠ HỌC HỆ NHIỀU VẬT 
Lại Thanh Tuấn*, Uông Sỹ Quyền, Trương Tư Hiếu 
Tóm tắt: Bài báo trình bày mô hình tính toán và khảo sát động lực học hệ robot-vũ khí 
trên cơ sở cơ học hệ nhiều vật. Phần robot gồm thân xe, giá súng, cơ cấu dẫn động và các 
bánh xe. Phần vũ khí là súng đại liên PKMS được liên kết với giá súng thông qua bộ phận 
định hướng chuyển động súng và lò xo giảm giật. Các kết quả nhận được cho phép đánh 
giá tính ổn định của cơ hệ robot-vũ khí, đồng thời làm cơ sở cho việc tính toán thiết kế, 
lắp đặt, bố trí các cơ cấu bộ phận để đảm bảo tính tối ưu của cơ hệ. 
Từ khóa: Robot chiến đấu; Động lực học; Súng đại liên PKMS; Ổn định. 
1. ĐẶT VẤN ĐỀ 
Ngày nay, cùng với những thành tựu đạt được trong lĩnh vực khoa học, công nghệ quân sự đặt 
ra những yêu cầu nghiên cứu các phương án chiến đấu tối ưu, cho phép giảm thiểu tối đa sự hiện 
diện trực tiếp của con người trên chiến trường. Việc lắp đặt súng tự động lên robot chiến đấu là 
một xu hướng nhằm thực hiện các nhiệm vụ đảm bảo cho người chiến sĩ được an toàn trong các 
không gian tác chiến đặc biệt. Tuy nhiên, sự kết hợp này phải tuân thủ các yêu cầu chiến kỹ thuật 
khắt khe, trong đó có yêu cầu về tính ổn định và đặc biệt là độ chính xác bắn của vũ khí. Vì vậy, 
việc khảo sát động lực học của hệ robot-vũ khí trong tác chiến là cơ sở quan trọng để xây dựng 
các tham số kết cấu của robot khi thiết kế nhằm thỏa mãn các nhiệm vụ thực tế đặt ra. 
2. XÂY DỰNG MÔ HÌNH TÍNH TOÁN VÀ KHẢO SÁT 
ĐỘNG LỰC HỌC HỆ ROBOT-VŨ KHÍ 
2.1. Xây dựng mô hình tính toán hệ robot chiến đấu-vũ khí 
Cơ hệ gồm hai phần: phần robot và phần vũ khí. Mô hình khảo sát được xây dựng dựa trên 
các giả thuyết: robot đứng yên trên mặt phẳng nằm ngang khi bắn; trừ các lò xo là các phần tử 
đàn hồi các vật còn lại được xem là các vật rắn tuyệt đối; không tính đến động năng và ảnh 
hưởng của bộ phận dẫn tiến; cơ cấu tầm-hướng được khóa cứng trong quá trình bắn và các liên 
kết được xem là lý tưởng, không có khe hở. Mô hình khảo sát (hình 1) gồm các vật: thân xe 
(khối lượng 1m , khối tâm tại 1O ), giá súng (khối lượng 2m , khối tâm 2O ), hộp súng (khối lượng 
3m , khối tâm 3O ), bệ khóa nòng (khối lượng 4m , khối tâm 4O ) và các khâu làm việc của máy tự 
động: cơ cấu tiếp đạn (khối lượng tdm ) và cơ cấu khóa nòng (khối lượng knm ) có dịch chuyển 
phụ thuộc vào chuyển động của khâu cơ sở. 
Để khảo sát ta sử dụng các hệ tọa độ: hệ tọa độ cố định 0 0 0 0O x y z gắn với trọng tâm xe trước 
khi bắn; các hệ tọa độ động 1 1 1 1O x y z gắn với thân xe, 2 2 2 2O x y z gắn với giá súng, 3 3 3 3O x y z gắn 
với hộp súng, 4 4 4 4O x y z gắn với bệ khóa nòng. Hướng của các trục tọa độ thể hiện như trên hình 
1. Các hệ tọa độ động kn kn kn knO x y z và td td td tdO x y z gắn với trọng tâm ban đầu của cơ cấu khóa 
nòng và cơ cấu tiếp đạn, có trục Ox song song với phương chuyển động của chúng, trục Oy 
hoặc Oz song song với trục tương ứng trên hệ 2O , trục còn lại hợp thành tam diện thuận. Với 
mục đích khảo sát dao động khi bắn của súng khi lắp trên robot, để đơn giản tính toán mà vẫn 
đảm bảo độ chính xác cơ hệ được khảo sát với các bậc tự do (tọa độ suy rộng): dịch chuyển tịnh 
tiến của trọng tâm xe 1q theo phương 1 1O x , dịch chuyển quay của hộp súng 2q quanh trục 2 2O z , 
dịch chuyển tịnh tiến của trọng tâm hộp súng 3q so với giá súng theo phương 3 3O x , dịch chuyển 
tịnh tiến của trọng tâm bệ khóa nòng 4q so với hộp súng theo phương 4 4O x . 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 151 
Hình 1. Mô hình cơ hệ robot-vũ khí. 
Hệ phương trình vi phân mô tả chuyển động của cơ hệ robot-vũ khí sử dụng phương pháp 
Lagrange có dạng: 
( ) ( )
j
j j
T Td
Q
dt q t q t
 
  
− = 
   
, 4j  (1) 
Trong đó: T - Tổng động năng cơ hệ; jq - Các tọa độ suy rộng; jQ - Các lực suy rộng tác 
dụng lên thân xe, giá súng, hộp súng, bệ khóa nòng. 
Để xác định lực của áp suất khí thuốc tác dụng trong lòng nòng ta giải bài toán thuật phóng 
trong, sử dụng hệ phương trình vi phân: 
 
1 3 1 3 2
2 3
2 3
2 3 3
; ; ;
(1 2 ) (1 ) ;
1
(1 2 ) ;
1 1
(1 2 ) (1 ) .
k
c
b b d
k
k
p b b d t
k
dv pS dl dz p
v
dt m dt dt I
d p
z G G
dt I
dw p
z sv
dt I
dp p
f Kp z KpSV K G G K p
dt w I
    

    
 
   

 
    

= = = 
= + − − − 
 −
 = + +
  − = − + − − + − −   
 (2) 
Áp suất khí thuốc trong buồng khí được xác định bởi hệ phương trình nhiệt động trong buồng 
khí dựa trên các quá trình cơ bản của khí động lực học: 
( ); ;
1
( ) .
b b
i b bk i b
b
b b b b i
b
d d
G G XS
dt dt
dp
kRTG kRT kp w
dt w
 
 

= − = 
 = − −
 (3) 
Bằng phương pháp số, giải đồng thời hệ các phương trình vi phân dao động (1) của hệ robot-
vũ khí, hệ các phương trình vi phân thuật phóng trong (2) và hệ các phương trình nhiệt động 
buồng khí sẽ cho phép ta nhận được các quy luật chuyển động của hệ khi bắn. Sơ đồ khối mô tả 
tính toán máy tự động kiểu trích khí thể hiện trên hình 2. 
Cơ kỹ thuật & Cơ khí động lực 
 152 L. T. Tuấn, U. S. Quyền, T. T. Hiếu, “Khảo sát động lực học  cơ sở cơ học hệ nhiều vật.” 
Hình 2. Sơ đồ khối mở rộng tính toán máy tự động kiểu trích khí. 
1 - Các điều kiện ban đầu; 2 - Xác định các lực tác dụng lên khâu cơ sở; 
3 - Xác định giá trị lực cản; 4 - Xác định giá trị Ki và ηi; 5,6 - Xác định các hệ số ξi; 
7 - Xét điều kiện xảy ra va chạm; 8 - Tính biến thiên tốc độ do va chạm; 
9 - Phân tích điều kiện kết thúc tính toán; 10 - Ghi kết quả; 11 - Dừng tính toán. 
2.2. Xác định động năng cơ hệ, công khả dĩ và các lực suy rộng 
Động năng của cơ hệ được xác định là tổng động năng của các vật: 
1 2 3 4 kn tdT T T T T T T = + + + + + (4) 
Trong đó: 
+ 1 1 1 1
1
2
TT R m R= - Động năng của thân xe; 
+ ( )2 32 2 2 2 0 2 0
1
2
T T TT R m R A I A = + - Động năng của giá súng; 
+ ( )3 33 3 3 3 0 3 0
1
2
T T TT R m R A I A = + , ( )4 44 4 4 4 0 4 0
1
2
T T TT R m R A I A = + - Động năng của hộp 
súng và bệ khóa nòng; 
+ ( )0 0
1
2
T T kn knT
kn kn kn kn knT R m R A I A = + , ( )0 0
1
2
T T td tdT
td td td td tdT R m R A I A = + - Động năng 
của cơ cấu khóa nòng và tiếp đạn. 
Ở đây: 
+ 1R , 2R , 3R , 4R , knR , tdR , 1m , 2m , 3m , 4m , knm , tdm - Thứ tự là véc tơ trọng tâm trong hệ 
tọa độ cố định 0O và ma trận khối lượng tương ứng của thân xe, giá súng, hộp súng, bệ khóa, cơ 
cấu khóa nòng và cơ cấu tiếp đạn; 
+ - Vận tốc góc quay của hộp súng trong mặt phẳng bắn; 
+ 2I , 3I , 4I , knI , tdI - Ten xơ quán tính của giá súng đối với hệ trục 2O , hộp súng đối với 
hệ trục 3O , bệ khóa nòng với hệ trục 4O , cơ cấu khóa nòng và cơ cấu tiếp đạn với hệ trục 
3
3 0 3 3
kn kn
kn iR R A U A U = + + và tdO . 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 153 
+  1 1 0 0
T
R q= ; 
+ 2 22 1 0 1R R A U= + ; 
+ 3 33 2 0 2R R A U= + ; 
+ 4 44 3 0 3R R A U= + ; 
+  30 20 0
T
A q = ; 
+ 33 0 3 3
kn kn
kn iR R A U A U = + + ; 
+ 33 0 3 3
td td
td iR R A U A U = + + ; 
+  21 21 21 21
T
U a b c= ; 
+  32 32 3 32 32
T
U a q b c= + ; 
+  43 43 4 43 43
T
U a q b c= + ; 
+  0 0
T
kn knU q= ; 
+  0 0
T
td tdU q= 
2
0A , 
3
0A , 
4
0A , 0
knA ; 
+ 0
knA - Các ma trận chuyển từ các hệ trục tọa độ 2O , 3O , 4O , knO , tdO về hệ trục tọa độ cố 
định 0O ; 
+ 21U , 
3
2U , 
4
3U , 3
knU , 3
tdU - Tương ứng là các véc tơ gốc 2O trong hệ trục 1O , véc tơ gốc 3O 
trong hệ trục 2O , véc tơ gốc 4O trong hệ trục 3O , véc tơ trọng tâm khóa nòng và tiếp đạn trong 
hệ tọa độ 3O : 
2 2
0 1A A= ; 
3 2 3
0 0 2.A A A= ; 
4 3
0 0A A= ; 
3
0 0 3
kn knA A A= ; 30 0 3
td tdA A A= ; 
+ 21A , 
3
2A , 3
knA , 3
tdA là các ma trận quay từ các hệ trục tọa độ 2O về 1O , từ hệ trục 3O về 
2O , từ hệ trục knO và tdO về 3O : 
2 2
2 3 ( )
1 2 3
2 2
1 0 0 cos 0 sin cos 0 sin
0 1 0 ; 0 1 0 ; 0 1 0
0 0 1 sin 0 cos sin 0 cos
kn td
q q
A A A
q q
= = = 
 − − 
; 
+ - Góc lệch của hướng chuyển động khâu khóa nòng hoặc tiếp đạn so với một trong các 
trục của hệ trục 3O . 
Tổng công khả dĩ của các lực suy rộng được tính theo công thức: 
4
lg
1
lx bk bxk td ph
k
W WP WF WG WP WP WF WF WF        
=
= + + + + + + + 
 (5) 
Trong đó : WP , lxWF , WG , lgWP , bkWP , bxkWF ( 1..4k = ), tdWF , phWF lần lượt 
là công khả dĩ của trọng lực, lực của lò xo đẩy về, lực của cơ cấu giảm giật, lực khí thuốc, lực 
của áp suất khí thuốc trong buồng khí tác dụng lên súng, lực đàn hồi của các bánh xe, lực cản 
băng đạn và lực cản phụ của máy tự động. 
Ở đây: 
+ 
4
1
i td kn
i
WP WP WP WP   
=
= + + ; 
+ Ti i izWP P R = ( 1..4i = ); 
Cơ kỹ thuật & Cơ khí động lực 
 154 L. T. Tuấn, U. S. Quyền, T. T. Hiếu, “Khảo sát động lực học  cơ sở cơ học hệ nhiều vật.” 
+ Tkn kn knzWP P R = ; 
+ Ttd td tdzWP P R = ; 
+ 
4
1
iz
iz j
jj
R
R q
q
 
=

=

 ; 
+ 
4
1
knz
knz j
jj
R
R q
q
 
=

=

 ; 
+ 
4
1
tdz
tdz j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của trọng tâm thân xe, giá súng, hộp súng, bệ khóa 
nòng, cơ cấu khóa nòng và cơ cấu tiếp đạn; 
+ ( )3 4lx lx lx lxWF F R R  = − − ; 
+ ( )4 40 4lxF K f q= + - Lực nén của lò xo đẩy về; 
+ 
34
3
1
lx
lx j
jj
R
R q
q
 
=

=

 và 
44
4
1
lx
lx j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của các điểm đặt lực trên hộp 
súng và bệ khóa nòng; 
+ 40f - Độ nén lò xo tương ứng vị trí 4 40q q= ; 
+ 3ggWG F R = ; 
+ 30 3( )gg ggF K f q= − - Lực nén của lò xo giảm giật; 
+ 
4
3
3
1
j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của thân súng; 
+ 30f - Độ nén ban đầu tương ứng vị trí cân bằng trước khi bắn ; 
+ 
lglg lg
T
PWP P R = ; 
+ lgP - Lực áp suất khí thuốc được tính theo hệ phương trình thuật phóng trong; 
+ 
lg
lg
4
1
P
P j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của điểm đặt lực lgP ; 
+ ( )3 4
bk bk
T
bk bk P PWP P R R  = − ; 
+ bkP - Lực áp suất khí thuốc trong buồng khí được xác định theo hệ phương trình nhiệt động 
buồng khí; 
+ 
34
3
1
bk
bk
P
P j
jj
R
R q
q
 
=

=

 , 
44
4
1
bk
bk
P
P j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của các điểm đặt lực bkP 
trong hệ tọa độ động 3O và 4O ; 
+ bxk bxk bxkWF F R = ; 
+ 10 1bxk z bxkF A F= 
- Lực tác dụng tại bánh xe k; 
+ 
4
1
bxk
bxk j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của điểm đặt lực bxkF ; 
+ 10zA - Ma trận quay quanh trục Oz từ hệ trục 1O về hệ trục 0O ; 
+ 1bxkF - Lực tác dụng tại bánh xe k trong hệ trục 1O ; 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 155 
+ Ttd td FtdWF F R = ; 
+ td bF K V n g = + - Lực cản băng đạn; 
+ 
4
1
Ftd
Ftd j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của điểm đặt lực cản băng đạn ; 
+ ( )3 4Tph ph ph phWF F R R  = − − ; 
+ phF - Lực cản phụ của máy tự động gồm: lực cản tống đạn, lực cản rút đạn và rút vỏ đạn, 
lực ma sát trên các đường trượt; 
+ 
34
3
1
ph
ph j
jj
R
R q
q
 
=

=

 , 
44
4
1
ph
ph j
jj
R
R q
q
 
=

=

 - Di chuyển khả dĩ của điểm đặt lực cản phụ 
trên hộp súng trong hệ tọa độ 3O và của bệ khóa nòng trong hệ tọa độ 4O . 
2.3. Giải bài toán động lực học cơ hệ robot-vũ khí 
Hệ phương trình vi phân để giải bài toán động lực học của cơ hệ gồm: hệ phương trình vi 
phân mô tả chuyển động của cơ hệ; hệ phương trình vi phân thuật phóng trong của súng đại liên 
PKMS và hệ phương trình nhiệt động buồng khí. Các số liệu đầu vào để giải bài toán thuật 
phóng trong và bài toán nhiệt động buồng khí của súng PKMS được lấy theo tài liệu [1]. Các số 
liệu đầu vào của cơ hệ robot-vũ khí được lấy từ các số liệu mô phỏng mô hình trên phần mềm đồ 
họa AutoDesk Inventor 2018: 1 1000P = N; 2 200P = N; 3 75.5P = N; 4 8.6P = N; 0.75tdP = N; 
1.47knP = N; 1 1.667xxJ = kg.m
2; 1 2.833yyJ = kg.m
2; 1 3.234zzJ = kg.m
2; 2 0.018xxJ = kg.m
2; 
2 0.018yyJ = kg.m
2; 2 0.014zzJ = kg.m
2; 3 0.01xxJ = kg.m
2; 3 0.27yyJ = kg.m
2; . . kg.m2; 
4 0.00014xxJ = kg.m
2; 4 0.009yyJ = kg.m
2; 4 0.008zzJ = kg.m
2; 
7325.10tdxx tdyy tdzzJ J J
−= = = 
kg.m2; 
8926.10knxx knyy knzzJ J J
−= = = kg.m2. Độ cứng của lò xo giảm xóc: 800gxK = N/m; độ 
cứng lò xo giảm giật: Kgg = 300ggK = N/m; độ cứng của lò xo đẩy về: 4 4K = N/m. Tọa độ 
trọng tâm các vật được xác định theo phần mềm mô phỏng cơ hệ. 
Sử dụng phần mềm Maple 18 để giải đồng thời các hệ phương trình của bài toán động lực 
học, ta nhận được quy luật áp suất khí thuốc, quy luật chuyển động của đạn, quy luật áp suất 
buồng khí, quy luật chuyển động của máy tự động và quy luật chuyển động của cơ hệ. Dưới đây 
dẫn ra các đồ thị: đồ thị áp suất thuật phóng trong của súng (hình 3); đồ thị mô tả chuyển động 
của khâu cơ sở theo thời gian (hình 4); đồ thị chuyển động của thân xe theo thời gian tương ứng 
với một phát bắn (hình 5a), với ba phát bắn (hình 5b) và đồ thị góc nảy thân xe theo thời gian khi 
bắn (hình 6). 
Hình 3. Đồ thị áp suất thuật phóng trong và 
áp suất buồng khí. 
Hình 4. Đồ thị mô tả chuyển động của 
khâu cơ sở theo thời gian. 
Cơ kỹ thuật & Cơ khí động lực 
 156 L. T. Tuấn, U. S. Quyền, T. T. Hiếu, “Khảo sát động lực học  cơ sở cơ học hệ nhiều vật.” 
a) Với một phát bắn b) Với ba phát bắn 
Hình 5. Đồ thị chuyển động của thân xe theo thời gian. 
Hình 6. Đồ thị góc nảy của súng theo thời gian khi bắn. 
Các kết quả tính toán thuật phóng trong và nhiệt động học buồng khí, chuyển động của khâu 
cơ sở nhận được tương đối sát với các số liệu công bố của nhà sản xuất. Dao động của thân súng 
so với giá thông qua cơ cấu giảm giật phụ thuộc vào thông số của cơ cấu giảm giật. Chu kỳ làm 
việc của cơ cấu giảm giật nhỏ hơn chu kỳ làm việc của máy tự động nên đảm bảo sự tiếp đạn và 
hoạt động của các cơ cấu giữa các phát bắn khác nhau không có nhiều sai khác. Thân xe khi bắn 
có dao động khoảng 0,04 mm khi bắn phát một và 0,14 mm khi bắn ba phát liên tiếp, sau đó trở 
lại vị trí cân bằng do có mô men quán tính và trọng lượng nên giúp robot ổn định hơn. 
3. KẾT LUẬN 
Trên cơ sở xây dựng mô hình cơ hệ robot-vũ khí, sử dụng lý thuyết cơ học hệ nhiều vật đã 
xây dựng hệ phương trình vi phân chuyển động của máy tự động súng đại liên PKMS lắp trên 
robot chiến đấu thông qua cơ cấu giảm giật bằng lò xo. Bằng phương pháp số giải đồng thời với 
hệ phương trình thuật phóng trong, hệ phương trình nhiệt động buồng khí đã xác định được dịch 
chuyển của hộp súng, thân xe và góc nảy của súng khi bắn. Các kết quả tính toán tương đối phù 
hợp với các số liệu lý thuyết, đảm bảo độ tin cậy nhất định và có thể dùng là cơ sở cho việc 
nghiên cứu động lực học vũ khí lắp trên robot chiến đấu cũng như khi tính toán thiết kế, cải tiến 
và tối ưu hóa hệ thống. 
TÀI LIỆU THAM KHẢO 
[1]. Trương Tư Hiếu, Uông Sỹ Quyền, “Trang bị điển hình vũ khí tự động”, NXB Học viện Kỹ thuật quân 
sự (2004). 
[2]. Võ Ngọc Anh, “Động lực học vũ khí tự động”, NXB Học viện Kỹ thuật quân sự (1995). 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 157 
[3]. Phạm Huy Chương, “Giáo trình cơ sở kết cấu và tính toán thiết kế máy tự động”, NXB Học viện Kỹ 
thuật quân sự (1998). 
[4]. “Hướng dẫn sử dụng súng PKMS”, Cục quân khí, Tổng cục Kỹ thuật. 
[5]. J. Wittenburg, “Động lực học hệ vật rắn” (Người dịch: GS TSKH Nguyễn Đông Anh), NXB Xây 
dựng (2000). 
ABSTRACT 
THE SURVEY OF DYNAMICS OF ROBOT-WEAPON SYSTEM 
BASED ON OF MECHANICS OF MULTIBODY SYSTEM 
The article presents a model for calculating and surveying dynamics of the robot-
weapon system based on of mechanics of the multibody system. The robot consists of the 
vehicle body, the gun rack, transmission structure and the wheels. The weapon is a 
machine gun PKMS, which is attached to the gun rack by the orientation bar and reduces 
shock springs. The results of the calculating allowed the assessment of the stability of the 
robot-weapon system and used as the basis for calculating for design, installation and 
arrangement of components with the optimization of the system. 
Keywords: Combat robot; Dynamics; Machine gun PKMS; Stability. 
Nhận bài ngày 17 tháng 01 năm 2021 
Hoàn thiện ngày 04 tháng 3 năm 2021 
Chấp nhận đăng ngày 12 tháng 4 năm 2021 
Địa chỉ: Bộ môn Vũ khí - Khoa Vũ khí - Học viện Kỹ thuật quân sự. 
*Email: thanhtuan711@gmail.com.