Giáo trình Robot công nghiệp - Chương 8: Thiết kế quỹ đạo robot

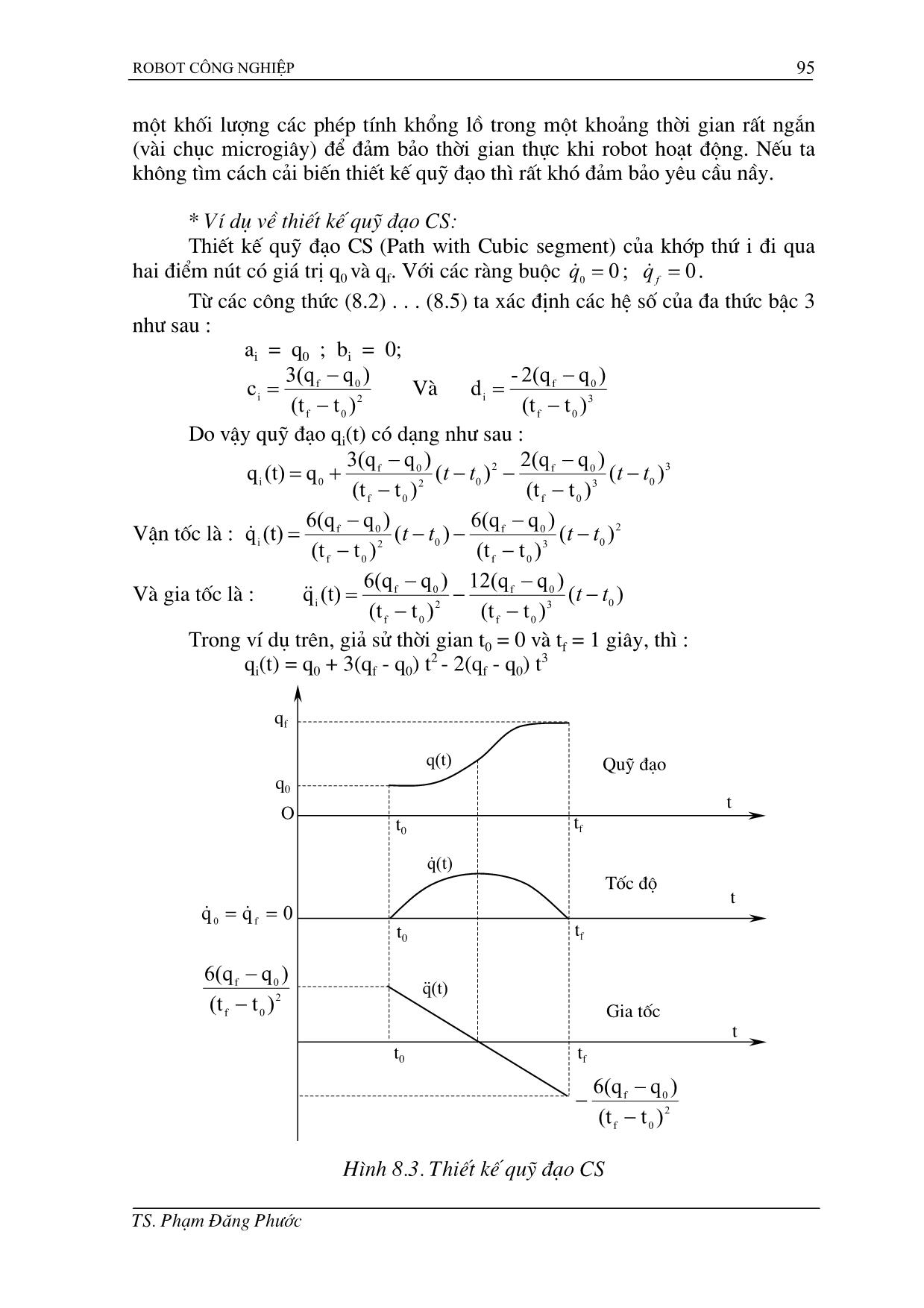
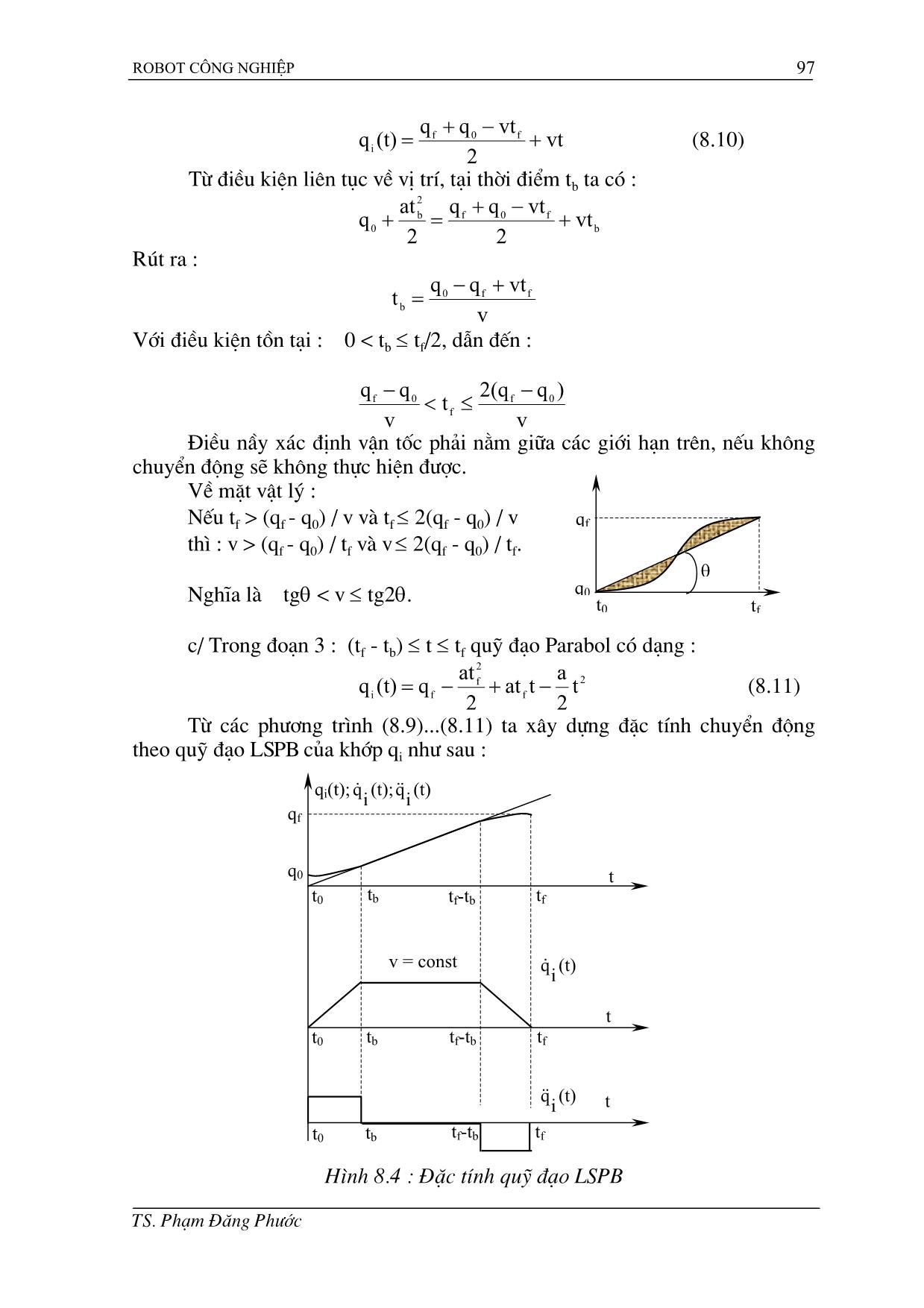
Robot công nghiệp 
92
Ch−ơng VIII 
Thiết kế quĩ đạo robot. 
(Trajectory Planing) 
Trong các ứng dụng công nghiệp của robot, ta th−ờng gặp hai tr−ờng 
hợp sau : 
Tr−ờng hợp 1 : Khâu chấp hành cuối của robot chỉ cần đạt đ−ợc vị trí và 
h−ớng tại các điểm nút (điểm tựa : Knot point). Đây chính là ph−ơng pháp 
điều khiển điểm (PTP). Tại đó, bàn tay robot thực hiện các thao tác cầm nắm 
đối t−ợng hoặc buông nhả đối t−ợng. Đây là tr−ờng hợp của các robot thực 
hiện công việc vận chuyển và trao đổi phôi liệu trong một hệ thống tự động 
linh hoạt robot hoá. Bàn tay robot không trực tiếp tham gia vào các nguyên 
công công nghệ nh− hàn, cắt kim loại ... Các điểm nút là mục tiêu quan trọng 
nhất, còn dạng đ−ờng đi tới các điểm nút là vấn đề thứ yếu. Trong tr−ờng hợp 
nầy Robot th−ờng đ−ợc lập trình bằng ph−ơng pháp dạy học (Teach and 
playback mode). Trong tr−ờng hợp nầy không cần tính toán ph−ơng trình động 
học hoặc động học ng−ợc robot, chuyển động mong muốn đ−ợc ghi lại nh− 
một tập hợp các góc khớp (thực tế là tập hợp các giá trị mã hoá của biến khớp) 
để robot thực hiện lại (Playback) khi làm việc. 
Tr−ờng hợp 2 : Khâu chấp hành cuối của robot phải xác định đ−ờng đi 
qua các điểm nút theo thời gian thực. Đó là tr−ờng hợp các tay máy trực tiếp 
thực hiện các nguyên công công nghệ nh− sơn, hàn, cắt kim loại ... Vấn đề 
thiết kế quỹ đạo cho các robot trong tr−ờng hợp nầy là rất quan trọng. Nó 
quyết định trực tiếp chất l−ợng thực hiện các nguyên công công nghệ mà robot 
đảm nhận. Trong ch−ơng nầy, chúng ta đề cập đến bài toán thiết kế quỹ đạo 
với một số quỹ đạo điển hình. Các quỹ đạo nầy không chỉ có ý nghĩa trong 
tr−ờng hợp ứng dụng thứ hai mà nó bao hàm một ý nghĩa chung cho mọi 
robot, vì ngay cả tr−ờng hợp đơn giản nh− các robot thuộc ứng dụng thứ nhất 
cũng thực hiện những chuyển động quỹ đạo cơ bản mà chúng ta sẽ nghiên cứu 
d−ới đây. 
8.1. Các khái niệm về quỹ đạo robot : 
 Để xác định đ−ợc đ−ờng đi mong muốn của robot theo thời gian, quỹ 
đạo có thể đ−ợc tính toán thiết kế trong một hệ toạ độ truyền thống Oxyz 
(Cartesian Space) hoặc thiết kế trong không gian biến khớp (không gian 
tr−ờng vectơ các toạ độ suy rộng của robot), chẳng hạn với robot 6 bậc tự do 
thì . [ TX ,.,,, 654321 θθθθθθ= ] Thiết kế quỹ đạo ở đây đ−ợc hiểu là xác định qui 
luật chuyển động của các biến khớp để điều khiển chuyển động của từng khớp 
và tổng hợp thành chuyển động chung của robot theo một quỹ đạo đã đ−ợc 
xác định. 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
93
 Quỹ đạo cần thiết kế nhất thiết phải đi qua một số điểm nút cho tr−ớc (ít 
nhất là điểm đầu và điểm cuối). Ngoài các điểm nút chính, ta còn có thể chọn 
thêm các điểm nút phụ gọi là điểm dẫn h−ớng (via point) để tránh các ch−ớng 
ngại vật. 
Khi thiết kế quỹ đạo trong không gian biến khớp, tại mỗi điểm nút phải 
xác định giá trị của các biến khớp bằng ph−ơng pháp tính toán động học 
ng−ợc. Thời gian yêu cầu của mỗi đoạn quỹ đạo (giữa 2 điểm nút) là giống 
nhau cho tất cả các khớp vì vậy yêu cầu tất cả các khớp phải đạt đến điểm nút 
đồng thời. Ngoài việc yêu cầu thời gian phải giống nhau cho các khớp, việc 
xác định các hàm quỹ đạo của mỗi biến khớp không phụ thuộc vào các hàm 
của các khớp khác. Vì vậy việc thiết kế quỹ đạo trong không gian biến khớp 
đơn giản và dễ tính toán hơn khi mô tả trong hệ toạ độ Đềcác. 
Quỹ đạo thiết kế phải đảm bảo các điều kiện liên tục (continous 
conditions) bao gồm : 
 + Liên tục về vị trí (Position) 
 + Liên tục về tốc độ (Velocity) 
 + Liên tục về gia tốc (Acceleration). 
qi(t2)...
x(t) 
t
xo 
xf-1
x1 
x2 
xf 
tf tf-1t2 t1 to 
Các điểm nút
Hình 8.1. Tính liên tục của quỹ đạo robot. 
 Để thiết kế quỹ đạo robot, ng−ời ta th−ờng dùng ph−ơng pháp xấp xỉ 
các đa thức bậc n, các quĩ đạo th−ờng gặp là : 
 + Quĩ đạo CS (Cubic Segment) : T−ơng đ−ơng đa thức bậc 3; 
 + Quỹ đạo LS (linear Segment) : T−ơng đ−ơng đa thức bậc 1; 
 + Quỹ đạo LSPB (Linear Segment with Parabolic Blend) : Phối hợp đa 
thức bậc 2 với đa thức bậc 1. 
Đoạn thẳng
q0 q2
q1
Đ−ờng cong bậc 2
qf 
Hình 8.2 : Quỹ đạo LSPB 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
94
+ Quỹ đạo BBPB (Bang Bang Parabolic Blend) : là tr−ờng hợp đặc biệt 
của quỹ đạo LSPB khi đoạn tuyến tính thu về bằng 0 và xuất hiện điểm 
uốn. 
Hình 8.2 : Quỹ đạo BBPB 
 Nếu cho tr−ớc nhiều điểm nút, ta có thể áp dụng nhiều dạng quỹ đạo cơ 
bản khác nhau cho một biến khớp. 
8.2. Quỹ đạo đa thức bậc 3 : 
Khi thiết kế quỹ đạo robot theo đa thức bậc 3 qua các điểm nút, mỗi 
đoạn quỹ đạo giữa hai điểm nút sẽ đ−ợc biểu diễn bằng một ph−ơng trình bậc 
3 riêng biệt. Quỹ đạo đa thức bậc 3 đảm bảo sự liên tục của đạo hàm bậc nhất 
và bậc hai tại các điểm nút. 
 Tại thời điểm tk ≤ t ≤ tk+1, quỹ đạo xấp xỉ đa thức bậc 3 của biến khớp 
thứ i là qi(t) có dạng : 
qi(t) = ai + bi(t - tk) + ci(t - tk)
2 + di(t - tk)
3 (8.1) 
Với các ràng buộc : 
 qi(tk) = qk và kki q )(tq && = 
qi(tk+1) = qk+1 và 1k1ki q )(tq ++ = && 
 Từ (8.1) ta thấy : t = tk → ai = qk (8.2) 
q0 
qf 
Bậc 3
tk+1tk 
qk 
qk+1
t 
qi(t)
 Lấy đạo hàm của (8.1) theo t, ta có : 
2
kikiii )t(t3d)t(t2cb(t)q −+−+=& 
 Tại : t = tk → (8.3) ki q b &=
 Tại t = ti+1 ta có hai tham số : 
2
k
k1kkk1k
i δt
δt )qq(2)q3(qc ++ +−−= && (8.4) 
3
k
k1kkk1k
i δt
 )q 2(qδt )qq(d −−+= ++ && (8.5) 
Trong đó : k1kk t t δt −= + 
 Các ph−ơng trình (8.4) và (8.5) nhận đ−ợc khi giải (8.1) ... (8.3). 
Tính liên tục của vận tốc là sự đảm bảo cho quỹ đạo không gấp khúc, 
giật cục, gây sốc trong quá trình hoạt động của robot. Vận tốc và gia tốc tại 
điểm cuối của một đoạn đ−ờng cong bậc 3 chính bằng vận tốc và gia tốc của 
đoạn cong bậc 3 tiếp theo. 
 Cần chú ý rằng khi thiết kế quỹ đạo trong không gian Đề cát, để điều 
khiển đ−ợc robot, ở mỗi thời điểm đều phải tìm đ−ợc nghiệm của bài toán 
động học ng−ợc. Vì vậy yêu cầu "não bộ" của robot (máy tính) phải thực hiện 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
95
một khối l−ợng các phép tính khổng lồ trong một khoảng thời gian rất ngắn 
(vài chục microgiây) để đảm bảo thời gian thực khi robot hoạt động. Nếu ta 
không tìm cách cải biến thiết kế quỹ đạo thì rất khó đảm bảo yêu cầu nầy. 
 * Ví dụ về thiết kế quỹ đạo CS: 
 Thiết kế quỹ đạo CS (Path with Cubic segment) của khớp thứ i đi qua 
hai điểm nút có giá trị q0 và qf. Với các ràng buộc 0 ; 00 == fqq && . 
 Từ các công thức (8.2) . . . (8.5) ta xác định các hệ số của đa thức bậc 3 
nh− sau : 
 ai = q0 ; bi = 0; 
 2
0f
0f
i )t(t
)q3(qc −
−= Và 3
0f
0f
i )t(t
)q2(q-d −
−= 
 Do vậy quỹ đạo qi(t) có dạng nh− sau : 
3
03
0f
0f2
02
0f
0f
0i )()t(t
)q2(q)(
)t(t
)q3(qq (t)q tttt −−
−−−−
−+= 
Vận tốc là : 203
0f
0f
02
0f
0f
i )()t(t
)q6(q)(
)t(t
)q6(q (t)q tttt −−
−−−−
−=& 
Và gia tốc là : )(
)t(t
)q12(q
)t(t
)q6(q (t)q 03
0f
0f
2
0f
0f
i tt −−
−−−
−=&& 
 Trong ví dụ trên, giả sử thời gian t0 = 0 và tf = 1 giây, thì : 
 qi(t) = q0 + 3(qf - q0) t
2 - 2(qf - q0) t
3
2
0f
0f
)t(t
)q6(q
−
−−
t
Tốc độ
Quỹ đạo
tf 
t
tf 
t
tf 
Gia tốc
(t)q&
(t)q&&2
0f
0f
)t(t
)q6(q
−
−
0qq f0 == &&
t0 
t0 
t0 
O
q0 
q(t)
qf 
Hình 8.3. Thiết kế quỹ đạo CS 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
96
 Từ các ph−ơng trình quỹ đạo, ph−ơng trình vận tốc và ph−ơng trình gia 
tốc ta xây dựng đ−ợc các biểu đồ đặc tính chuyển động của khớp thứ i trên 
đoạn quỹ đạo thiết kế. 
8.3. Quỹ đạo tuyến tính với cung ở hai đầu là parabol (LSPB) : 
 Khi yêu cầu công cụ gắn trên khâu chấp hành cuối của robot chuyển 
động với vận tốc đều đặn, ta dùng quỹ đạo LSPB. 
qi(t) 
tf tf - tbtf/2tb 
v = constant
d
Parabol c 
O t0 
Parabol 
e
t 
 (q0+qf)/2 
Hình 8.3. Quỹ đạo LSPB. 
 Các điều kiện liên tục của quỹ đạo nầy thể hiện ở : 
q(to) = q0 ; q(tf) = qf; và 0 )(tq )(q f0 == && t 
 và điều kiện công nghệ là v = constant. 
 Quỹ đạo đ−ợc chia làm 3 đoạn : 
 a/ Trong đoạn 1 : 0 ≤ t ≤ tb quỹ đạo Parabol có dạng : 
 qi(t) = α + βt + γt2 (8.6) 
 Khi t = 0 thì α = q(t0) = q0 (8.7) 
Lấy đạo hàm (8.6) : t2γβ(t)q +=& (8.8) 
 Khi t = 0 thì 0 )(tq β o == & 
Tại thời điểm tb ta cần có vận tốc bằng hằng số vận tốc cho tr−ớc v : 
 Nên khi t = tb γ = v/2tb
 Đặt v/tb = a ⇒ γ = a/2 và quỹ đạo có dạng : 
qi(t) = q0 + at
2/2 (0 ≤ t ≤ tb) (8.9) 
 b/ Trong đoạn 2 : [tb, (tf-tb)] quỹ đạo tuyến tính có dạng : 
 qi(t) = α0 + vt 
 Do tính đối xứng : 
2
)q(q)
2
t(q f0f += 
 Suy ra 
2
tvα
2
)q(q f
0
f0 +=+ 
 Vậy 
2
)vtq(qα ff00
−+= 
 Ph−ơng trình quỹ đạo tuyến tính sẽ là : 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
97
vt
2
vtqq(t)q f0fi +−+= (8.10) 
 Từ điều kiện liên tục về vị trí, tại thời điểm tb ta có : 
b
f0f
2
b
0 vt2
vtqq
2
atq +−+=+ 
Rút ra : 
v
vtqqt ff0b
+−= 
Với điều kiện tồn tại : 0 < tb ≤ tf/2, dẫn đến : 
v
)q2(qt
v
qq 0f
f
0f −≤<− 
 Điều nầy xác định vận tốc phải nằm giữa các giới hạn trên, nếu không 
chuyển động sẽ không thực hiện đ−ợc. 
 Về mặt vật lý : 
 Nếu tf > (qf - q0) / v và tf ≤ 2(qf - q0) / v 
 thì : v > (qf - q0) / tf và v ≤ 2(qf - q0) / tf. 
 Nghĩa là tgθ < v ≤ tg2θ. 
 c/ Trong đoạn 3 : (tf - tb) ≤ t ≤ tf quỹ đạo Parabol có dạng : 
 2f
2
f
fi t2
atat
2
atq(t)q −+−= (8.11) 
 Từ các ph−ơng trình (8.9)...(8.11) ta xây dựng đặc tính chuyển động 
theo quỹ đạo LSPB của khớp qi nh− sau : 
 (t) iq&
 ( iq&& t)
θ
tft0
q0
qf
t 
t 
t 
qi(t); q 
v = const
tf 
tf 
tf 
tf-tb 
tf-tb 
tf-tb 
tb 
tb 
tb 
t0 
t0 
t0 
q0 
(t)iq(t);i &&&
qf 
Hình 8.4 : Đặc tính quỹ đạo LSPB 
TS. Phạm Đăng Ph−ớc 
Robot công nghiệp 
98
8.4. Quỹ đạo Bang Bang Parabolic blend (BBPB) : 
 Nh− đã trình bày ở trên, đây là tr−ờng hợp đặc biệt của quỹ đạo LSPB 
khi đoạn tuyến tính thu về 0. 
 Với : 0 ≤ t ≤ 
2
tf qi(t) = q0 + 2
at2
 và với 
2
tf ≤ t ≤ tf qi(t) = 2q0 - qf +2a 2
at-t
a
qq 20f − 
 Đồ thị đặc tính của quỹ đạo nầy nh− sau : 
(t)iq&&
(t)iq&
Vmax
t 
t 
t 
tf 
tf 
tf 
tf/2
tf/2
tf/2
t0 
t0 
t0 
qf 
q0 
qi(t) 
Hình 8.5. Đặc tính quỹ đạo BBPB 
======================= 
TS. Phạm Đăng Ph−ớc