Giải pháp nâng cao độ chính xác định vị dựa trên kết quả định hướng và thông tin tiên nghiệm địa hình

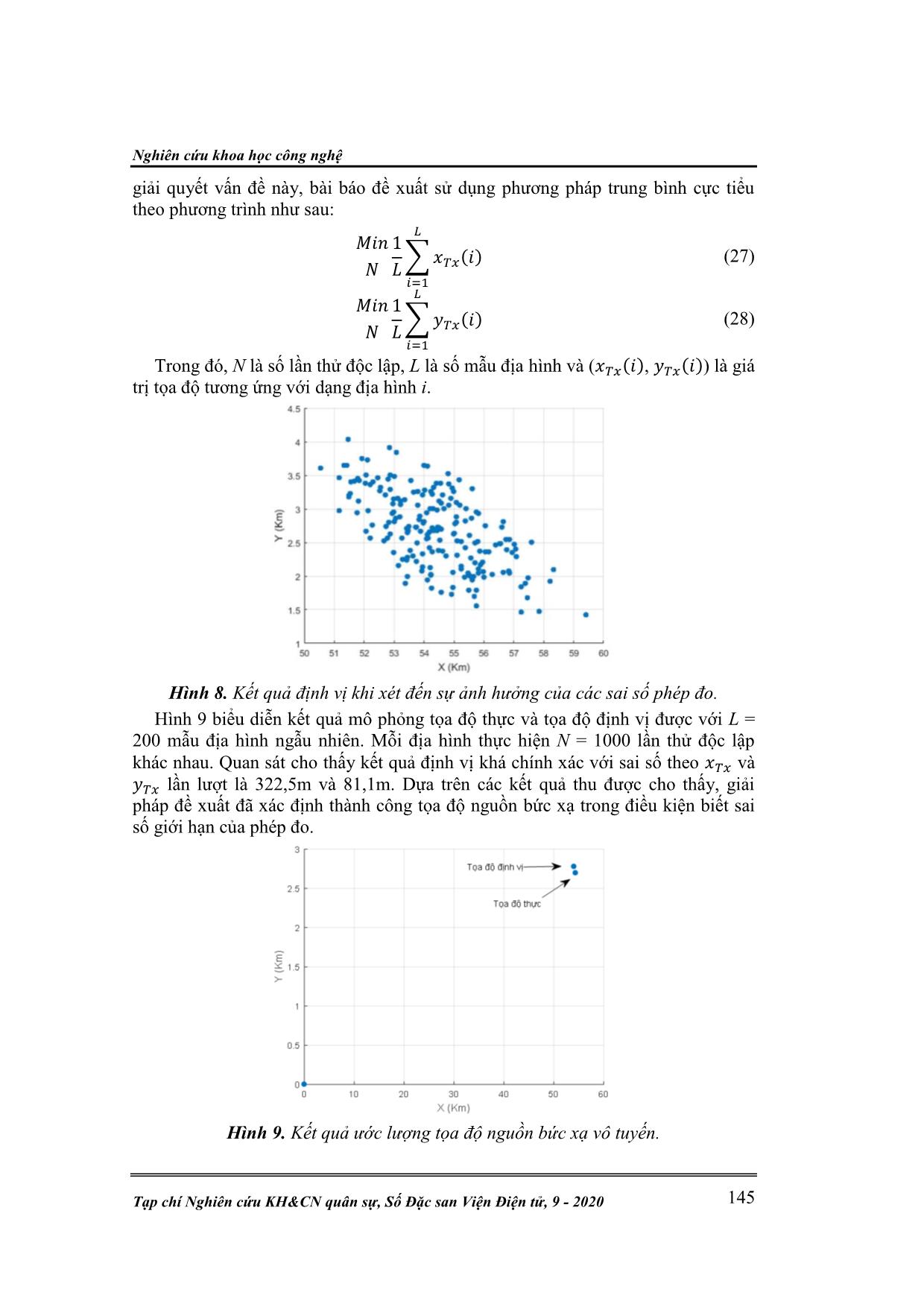
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 139 
GIẢI PHÁP NÂNG CAO ĐỘ CHÍNH XÁC ĐỊNH VỊ DỰA TRÊN 
KẾT QUẢ ĐỊNH HƯỚNG VÀ THÔNG TIN TIÊN NGHIỆM ĐỊA HÌNH 
Lê Thanh Hải, Nguyễn Tuấn Minh* 
Tóm tắt: Bài báo trình bày giải pháp định vị dựa trên kết quả định hướng góc 
phương vị và các tham số địa hình. Giải pháp này phù hợp trong môi trường truyền 
dẫn chỉ có các tín hiệu phản xạ tới máy thu. Thông tin tiên nghiệm địa hình được 
mô hình hoá dựa trên các tham số mặt phản xạ. Bên cạnh đó, bài báo cũng trình 
bày mô hình định vị 3D áp dụng giải pháp này trong thực tế và đề xuất giải pháp 
nâng cao độ chính xác định vị dựa trên giới hạn sai số các phép đo. Hiệu quả của 
giải pháp đề xuất được kiểm chứng trên phần mềm Matlab. 
Từ khóa: LOS; NLOS; Góc phương vị; Mặt phản xạ; Trung bình cực tiểu. 
1. MỞ ĐẦU 
Trong các bài toán định vị, các tín hiệu đặc trưng được xét đến là LOS hoặc 
NLOS. Các phương pháp, thuật toán sử dụng tín hiệu LOS đã được nghiên cứu 
nhiều như: RSSI [1]; AOA [2, 3], TOA [4]; TDOA [5]; RSSI-DOA [6]. Theo đó, 
môi trường truyền tín hiệu phải đáp ứng điều kiện không có vật cản giữa nguồn 
bức xạ và máy thu hoặc sự ảnh hưởng của vật cản lên tín hiệu vô tuyến là không 
đáng kể. Trong trường hợp NLOS, kết quả định vị không đảm bảo độ chính xác do 
ảnh hưởng của vật cản đến cường độ tín hiệu là rất lớn. Đã có một số các công 
trình nghiên cứu nhằm giải bài toán định vị trong địa hình có cả tín hiệu LOS và 
NLOS [7, 8]. Với địa hình chỉ có tín hiệu NLOS, phần lớn các tín hiệu thu được tại 
máy thu là do hiện tượng phản xạ. Phương pháp định vị sử dụng tín hiệu phản xạ 
đã được đề cập trong nghiên cứu [9], trong đó sử dụng mô hình truyền tín hiệu kết 
hợp với kỹ thuật đo chỉ số cường độ tín hiệu (RSSI) theo độ suy hao tín hiệu 
(Pathloss). Trong thực tế, thông tin tiên nghiệm về công suất phát, tần số hoạt động 
và dạng điều chế tín hiệu của nguồn bức xạ có thể không biết trước nên việc định 
vị dựa vào các tham số này vẫn là một khó khăn lớn. Với bối cảnh đó, bài báo này 
trình bày giải pháp định vị dựa trên kết quả định hướng và thông tin tiên nghiệm 
địa hình và đề xuất giải pháp nâng cao độ chính xác định vị. 
2. NỘI DUNG CẦN GIẢI QUYẾT 
 2.1. Xây dựng lý thuyết 
Hình 1 biểu diễn một dạng mô hình truyền tín hiệu bị che khuất hoàn toàn bởi 
yếu tố địa hình trong hệ tọa độ oxy với véc tơ ox là đường phương vị chuẩn (có 
góc phương vị bằng không) chung đối với tất cả các góc. Xét một nguồn bức xạ 
đặt tại vị trí cố định Tx có tọa độ (xTx, yTx) phát tín hiệu tới hai bề mặt phản xạ 
tương ứng với hai góc phương vị là β1 và β2. Giả thiết các bề mặt phản xạ là phẳng 
có kích thước đủ lớn để thỏa mãn điều kiện phản xạ [9, 10] và các tín hiệu tới máy 
thu chỉ đến từ một nguồn bức xạ duy nhất. Ngoài ra, trong phạm vi nghiên cứu chỉ 
xét đến trường hợp một lần phản xạ tín hiệu. Gọi α1 và α2 lần lượt là là các góc 
phương vị của véc tơ pháp tuyến n1 và n2. Giả sử máy thu tại vị trí Rx có tọa độ 
(xRx, yRx) thu nhận được tối thiểu hai tín hiệu đến từ hai bề mặt phản xạ với các góc 
phương vị tương ứng là ϕ1 và ϕ2. Gọi PPx1 và PPx2 là hai điểm phản xạ có tọa độ là 
(xPx1, yPx1) và (xPx2, yPx2). Khi đó: 
Kỹ thuật điện tử 
L. T. Hải, N. T. Minh, “Giải pháp nâng cao độ chính xác  tiên nghiệm địa hình.” 140 
 ( ) (1) 
 ( ) (2) 
Tx
Rx
PPx1
ϕ1
α1
n2
o
y
PPx2
ϕ2 α2
β1
β2
n1
x
β1
β2 
Hình 1. Mô hình địa hình có hai tín hiệu NLOS với một mặt phản xạ nằm trong 
góc phần tư thứ nhất và một mặt phản xạ nằm trong góc phần tư thứ hai. 
Hệ phương trình (1) và (2) gồm hai tham số và chưa biết nên không thể 
tìm được nghiệm duy nhất. Tuy nhiên, với thông tin tiên nghiệm địa hình đã biết 
thì hoàn toàn có thể xác định được các tham số α1 và α2. Tuỳ theo vị trí các mặt 
phản xạ so với đường phương vị chuẩn sẽ có các dạng địa hình tương ứng khác 
nhau, như miêu tả ở hình 1, 2, 3, và 4. 
 Tx
Rx
PPx1
ϕ1 α1
n2
o
y
PPx2
ϕ2 α2
β1
β2
n1
x
β1
β2
Hình 2. Mô hình địa hình có hai tín hiệu NLOS với hai mặt phản xạ 
nằm trong góc phần tư thứ nhất. 
Tx
Rx
PPx1
ϕ1
α1
n2
PPx2
ϕ2
α2
β1
β2
n1
β1
β2
x
o
y
Hình 3. Mô hình địa hình có hai tín hiệu NLOS với một mặt phản xạ nằm trong 
góc phần tư thứ nhất và một mặt phản xạ nằm trong góc phần tư thứ ba. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 141 
Tx
Rx
PPx1
ϕ1 α1
n2
PPx2
ϕ2
α2
β1
β2
n1
β1
β2
x
y
o
Hình 4. Mô hình địa hình có hai tín hiệu NLOS với một mặt phản xạ nằm trong 
góc phần tư thứ nhất và một mặt phản xạ nằm trong góc phần tư thứ tư. 
Khi xem xét với tất cả các trường hợp địa hình ở trên ta thu được kết quả tổng 
quát như sau: 
 (3) 
 (4) 
Do đó: 
 ( ) (5) 
 ( ) (6) 
Thực hiện biến đổi phương trình (5) và (6) thu được: 
Ax = B (7) 
Trong đó: 
 [
] (8) 
 [
 ( ) 
 ( ) 
] (9) 
 [
 ( ) 
 ( ) 
] (10) 
Với: 
 ( )( ) (11) 
 ( )( ) (12) 
Nhận thấy rằng, tọa độ nguồn bức xạ phụ thuộc vào bộ tham số ( , , , 
 , , , , ). Trong đó: 
- và xác định được nhờ sử dụng máy thu định hướng; 
- và xác định được nhờ sử dụng thiết bị định vị; 
- , , , xác định được dựa trên mô hình địa hình cụ thể. 
Trong trường hợp có nhiều hơn hai tín hiệu phản xạ tới máy thu như miêu tả 
trong hình 5 thì tọa độ nguồn bức xạ là giao hội của ba đường thẳng. Khi đó, toạ 
độ nguồn bức xạ có thể là ba điểm A, B hoặc C nên không thể định vị được chính 
xác. Để giải quyết hiện tượng đa trị này thường có các giải pháp như sau: 
- Sử dụng thông tin nghiệm về vị trí nguồn bức xạ; 
Kỹ thuật điện tử 
L. T. Hải, N. T. Minh, “Giải pháp nâng cao độ chính xác  tiên nghiệm địa hình.” 142 
- Sử dụng phương pháp dự đoán để loại trừ các tọa độ không phù hợp trên mô 
hình địa hình và phương pháp lấy trọng tâm giữa các điểm để xác định tọa độ gần 
đúng. 
Rx
PPx1
o
y
PPx2
x
PPx3
A
B
C
Hình 5. Mô hình địa hình có ba tín hiệu NLOS. 
2.2. Mô hình định vị 3D dựa trên kết quả định hướng và thông tin tiên nghiệm 
địa hình 
Hình 6 miêu tả mô hình tổng quát nguyên lý định vị sử dụng mô hình địa hình 
3D. Việc kết hợp các thông tin về tọa độ máy thu, góc phương vị các tín hiệu tới và 
mô hình địa hình 3D sẽ cho phép xác định được các đối tượng phản xạ. Sử dụng 
phương pháp nội suy để trích xuất các thông tin liên quan đến các đối tượng phản 
xạ như: Tọa độ điểm phản xạ, góc phương vị của pháp tuyến bề mặt phản xạ. Qúa 
trình thực hiện này có thể được thực hiện theo hai cách thông thường như sau: Sử 
dụng thuật toán Ray-Tracer [11] hoặc phần mềm Google Earth. 
Trích xuất thông tin 
đối tượng phản xạ: Tọa 
độ, góc pháp tuyến, 
góc lệch
Tọa độ máy thu 
và góc phương vị 
tín hiệu tới
Mô hình địa hình 3D với hệ tọa độ GPS
Xác định 
đối tượng phản xạ
Tọa độ 
nguồn bức xạ
Sử dụng giải 
pháp định vị 
đề xuất
Hình 6. Giải pháp định vị dựa trên mô hình địa hình 3D. 
- Giải pháp định vị tự động sử dụng thuật toán dò tia Ray-Tracer. Khi đó, tín 
hiệu được giả định như một tia sáng đặt tại vị trí máy thu với góc phương vị là góc 
của tia. Thuật toán Ray-Tracer minh họa trên hình 7 được thực hiện theo trình tự các 
bước như sau: 
(1) Tọa độ: Xác định tọa độ máy thu Rx (xRx, yRx); 
(2) Tạo tia: Gốc của tia là tọa độ máy thu, hướng của tia là góc phương vị của 
tín hiệu tới máy thu; 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 143 
(3) Xác định đối tượng: Việc xác định đối tượng phản xạ được dựa trên hàm xác 
định giao điểm của tia và vật thể, hàm tính véc tơ trực chuẩn tại một điểm trên vật thể; 
(4) Danh sách đối tượng: Bao gồm tất cả các đối tượng phản xạ đã xác định được; 
(5) Các thông tin về đối tượng sử dụng mô hình địa hình 3D để xác định các 
tham số về các đối tượng như dạng bề mặt phản xạ, tọa độ điểm phản xạ và góc 
phương vị của pháp tuyến bề mặt phản xạ. 
Tọa độ Tạo tia
Xác định 
đối tượng
Danh sách 
đối tượng
Các thông tin 
về đối tượng
Hình 7. Mô hình sử dụng thuật toán Ray-Tracer. 
 - Giải pháp định vị trên phần mềm Google Earth: Đây là phần mềm mô phỏng 
địa hình trái đất trong không gian ba chiều với hướng Bắc được chọn là hướng 
phương vị chuẩn. Những tính năng sẵn có của phần mềm này cho phép xác định 
được các thông tin về địa hình như tọa độ, độ cao, chiều dài giữa hai điểm, kích 
thước cũng như góc phương vị của pháp tuyến đối với một bề mặt cụ thể,... 
2.3. Đề xuất giải pháp nâng cao độ chính xác định vị dựa trên kết quả định 
hướng và thông tin tiên nghiệm địa hình 
Trong thực tế, bộ tham số để xác định tọa độ nguồn bức xạ được xác định như sau: 
 (13) 
 (14) 
 (15) 
 (16) 
 (17) 
 (18) 
 (19) 
 (20) 
Trong đó: 
 , 
 là góc phương vị thực của pháp tuyến mặt phản xạ 1 và 2; 
 , 
 là góc phương vị thực của hai tín hiệu phản xạ tới máy thu; 
 , 
 là tọa độ 
thực của điểm phản xạ 1 và 2; 
 , 
 là tọa độ thực của máy thu; , là sai 
số phương vị của pháp tuyến n1 và n2; , là sai số tọa độ điểm phản xạ 1 
và 2; , là sai số kết quả định hướng; , là sai số tọa độ máy thu. 
Khi đó, tọa độ nguồn bức xạ Tx’( 
 , 
 ) được xác định bởi phương trình sau: 
A’x’ = B’ (21) 
Ở đây: 
 [
 ] (22) 
 [
 [( 
 ) ( )] 
 [( 
 ) ( )] 
] (23) 
 [
 [( 
 ) ( )]( 
 ) 
 [( 
 ) ( )]( 
 ) 
] (24) 
Kỹ thuật điện tử 
L. T. Hải, N. T. Minh, “Giải pháp nâng cao độ chính xác  tiên nghiệm địa hình.” 144 
Với: 
 ( 
 )[( 
 ) ( )] (25) 
 ( 
 )[( 
 ) ( )] (26) 
Nhận thấy rằng, kết quả định vị phụ thuộc nhiều vào các sai số của bề mặt phản 
xạ, sai số trong xác định hướng của tín hiệu phản xạ tới máy thu và sai số toạ độ 
máy thu. Các sai số là các đại lượng ngẫu nhiên nên sai số tọa độ nguồn bức xạ 
cũng ngẫu nhiên. 
3. MÔ PHỎNG, TÍNH TOÁN, THẢO LUẬN 
3.1. Số liệu đầu vào 
Giả thiết mô hình địa hình có hai tín hiệu NLOS với hai mặt phản xạ nằm trong 
góc phần tư thứ nhất có các giá trị như trong bảng 1 và sai số giới hạn của mỗi 
phép đo như trong bảng 2. 
Bảng 1. Bảng tham số tương ứng với mô hình địa hình có hai tín hiệu NLOS 
với hai mặt phản xạ nằm trong góc phần tư thứ nhất. 
Tham số Giá trị Ý nghĩa 
ϕ1 17,5 Góc phương vị 1 tại máy thu (độ) 
ϕ2 44,3 Góc phương vị 2 tại máy thu (độ) 
α1 7 Góc phương vị của pháp tuyến n1 (độ) 
α2 11 Góc phương vị của pháp tuyến n2 (độ) 
xPx1 15,5 Tọa độ theo phương x điểm phản xạ 1 (km) 
xPx2 18,2 Tọa độ theo phương x điểm phản xạ 2 (km) 
(xRx, yRx) (0,8; 0,5) Tọa độ máy thu (km) 
Bảng 2. Bảng sai số giới hạn phương pháp đo. 
Tham số Giá trị Ý nghĩa 
 , ± 0,5 Sai số giới hạn góc pháp tuyến bề mặt phản xạ (độ) 
 , ± 0,2 Sai số giới hạn góc phương vị (độ) 
 , ± 40 Sai số giới hạn tọa độ phản xạ (m) 
 , ± 0,5 Sai số giới hạn tọa độ máy thu (m) 
3.2. Phương pháp, công cụ mô phỏng 
Trong thực tế, sai số đối với các giới hạn phương pháp đo là các đại lượng ngẫu 
nhiên. Do đó, bài báo thực hiện mô phỏng trên phần mềm Matlab theo phương 
pháp Monter – Carlo với nhiều các lần thử độc lập tương ứng với các mẫu địa hình 
khác nhau. 
3.3. Kết quả mô phỏng và bình luận 
Kết quả mô phỏng trên hình 8 biểu diễn kết quả định vị tương ứng với 200 mẫu 
địa hình ngẫu nhiên. 
Nhận thấy rằng, tọa độ nguồn bức xạ là tập hợp các điểm có phân bố rải rác khá 
rộng trong không gian. Khi đó không thể xác định được tọa độ nguồn bức xạ. Để 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 145 
giải quyết vấn đề này, bài báo đề xuất sử dụng phương pháp trung bình cực tiểu 
theo phương trình như sau: 
∑ ( )
 (27) 
∑ ( )
 (28) 
Trong đó, N là số lần thử độc lập, L là số mẫu địa hình và ( ( ), ( )) là giá 
trị tọa độ tương ứng với dạng địa hình i. 
Hình 8. Kết quả định vị khi xét đến sự ảnh hưởng của các sai số phép đo. 
Hình 9 biểu diễn kết quả mô phỏng tọa độ thực và tọa độ định vị được với L = 
200 mẫu địa hình ngẫu nhiên. Mỗi địa hình thực hiện N = 1000 lần thử độc lập 
khác nhau. Quan sát cho thấy kết quả định vị khá chính xác với sai số theo và 
 lần lượt là 322,5m và 81,1m. Dựa trên các kết quả thu được cho thấy, giải 
pháp đề xuất đã xác định thành công tọa độ nguồn bức xạ trong điều kiện biết sai 
số giới hạn của phép đo. 
Hình 9. Kết quả ước lượng tọa độ nguồn bức xạ vô tuyến. 
Kỹ thuật điện tử 
L. T. Hải, N. T. Minh, “Giải pháp nâng cao độ chính xác  tiên nghiệm địa hình.” 146 
4. KẾT LUẬN 
Bài báo đã trình bày giải pháp định vị dựa trên kết quả định hướng và thông tin 
tiên nghiệm địa hình trong điều kiện chỉ có tín hiệu NLOS. Giải pháp này có thể 
được áp dụng dựa trên mô hình 3D sử dụng thuật toán Ray-Tracer hoặc phần mềm 
Google Earth. Bên cạnh đó, bài báo cũng đề xuất giải pháp nâng cao độ chính xác 
định vị dựa trên giới hạn sai số các phép đo sử dụng phương pháp trung bình cực 
tiểu. Các kết quả thu được cho thấy giải pháp đề xuất đã xác định thành công tọa 
độ nguồn bức xạ vô tuyến. Trong thực tế, để cải thiện độ chính xác định vị cần sử 
dụng thiết bị định hướng và tiếp tục nghiên cứu xây dựng mô hình bộ dữ liệu tham 
số địa hình có độ chính xác cao. 
TÀI LIỆU THAM KHẢO 
[1]. Konrad L. and Matt W. (2007), “A Robust, decentralized approach to RF-
Based Location Tracking”, Personal and Ubiquitous Computing, vol. 11, no. 
6, pp. 489-503. 
[2]. Evans J. E., Johnson J. R., Sun D. F (1981), “High Resolution Angular 
Spectrum Estimation Techniques for Terrain Scattering Analysis and Angle of 
Arrival Estimation”, Proceedings 1st ASSP Workshop Spectral Estimation, 
pp. 134–139. 
[3]. Girod L., Lukac M., Trifa V. and Estrin D. (2006), “The Design and 
Implementation of a Self-Calibrating Distributed Acoustic Sensing Platform”, 
Proc. Fourth Int’l Conf. Embedded Networked Sensor Systems, pp. 71-84. 
[4]. Goud P., Sesay A. and Fattouche M. (1991), “A Spread Spectrum Radiolocation 
Technique and Its Application to Cellular Radio”, Proc. IEEE Pacific Rim Conf. 
Comm., Computers and Signal Processing, vol. 2, pp. 661-664. 
[5]. Jin B., Xu X. and Zhang T. (2018), “Robust Time-Difference-of-Arrival 
(TDOA) Localization Using Weighted Least Squares with Cone Tangent 
Plane Constraint”, Sensors, 18, 778. 
[6]. Dai F., Liu Y. and Chen L. (2012), “A Hybrid Localization Algorithm for 
Improving Accuracy Based on RSSI/AOA in Wireless Network”, International 
Conference on Computer Science & Service System (CSSS). 
[7]. Schroeder J., Galler S., Kyamakya K. and Jobmann K. (2007), “NLOS 
detection algorithms for ultra-wideband localization”, 4th Workshop on 
Positioning, Navigation and Communication, pp. 159 –166. 
[8]. Venkatraman S. and Caffery J. (2002), “Location using LOS range 
estimation in NLOS environments”, Vehicular Technology Conference, IEEE 
55th, vol. 2, pp. 856 – 860. 
[9]. Wielandt S. and Strycker L. (2017), “Indoor Multipath Assisted Angle of Arrival 
Localization”, Sensors. 
[10]. Popovic Z. B. and Popovic B. D. (2000), “Introductory Electromagnetics”, 
Prentice Hall: Upper Saddle River, NJ, USA. 
[11]. Yun Z. and Iskander M.F. (2005), “Characterization of angle of arrival 
based on ray-tracing for an indoor wireless communications environment”, 
IEEE/ACES International Conference on Wireless Communications and 
Applied Computational Electromagnetics, pp. 736–739. 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san Viện Điện tử, 9 - 2020 147 
ABSTRACT 
SOLUTIONS TO IMPROVE THE ACCURACY OF 
RADIO SOURCE NAVIGATION BASED ON DIRECTION FINDING 
RESULTS AND A-PRIORI INFORMATION OF TOMOGRAPHY 
In this paper, a radio source navigation solution based on azimuth and 
topographic parameters is presented. The approach is suitable for the 
transmission environment with only reflected signals to the receiver. The a-
priori information of tomography is modeled based on reflective surface 
parameters. In addition, a 3D positioning model allowing the application 
of this solution in practice and propose a solution to improve the 
positioning accuracy based on the measurement of error limits is also 
presented in the paper. The effectiveness of the proposed solution is 
verified using Matlab simulation. 
Keywords: LOS; NLOS; Azimuth; Reflective surface; Minimum average. 
Nhận bài ngày 29 tháng 4 năm 2020 
Hoàn thiện ngày 30 tháng 7 năm 2020 
Chấp nhận đăng ngày 28 tháng 8 năm 2020 
Địa chỉ: Viện Điện tử - Viện Khoa học và Công nghệ quân sự. 
*Email: ntminh.telecom@gmail.com.