Điều khiển bám quỹ đạo cho xe tự hành sử dụng bộ điều khiển thích nghi mờ loại 2

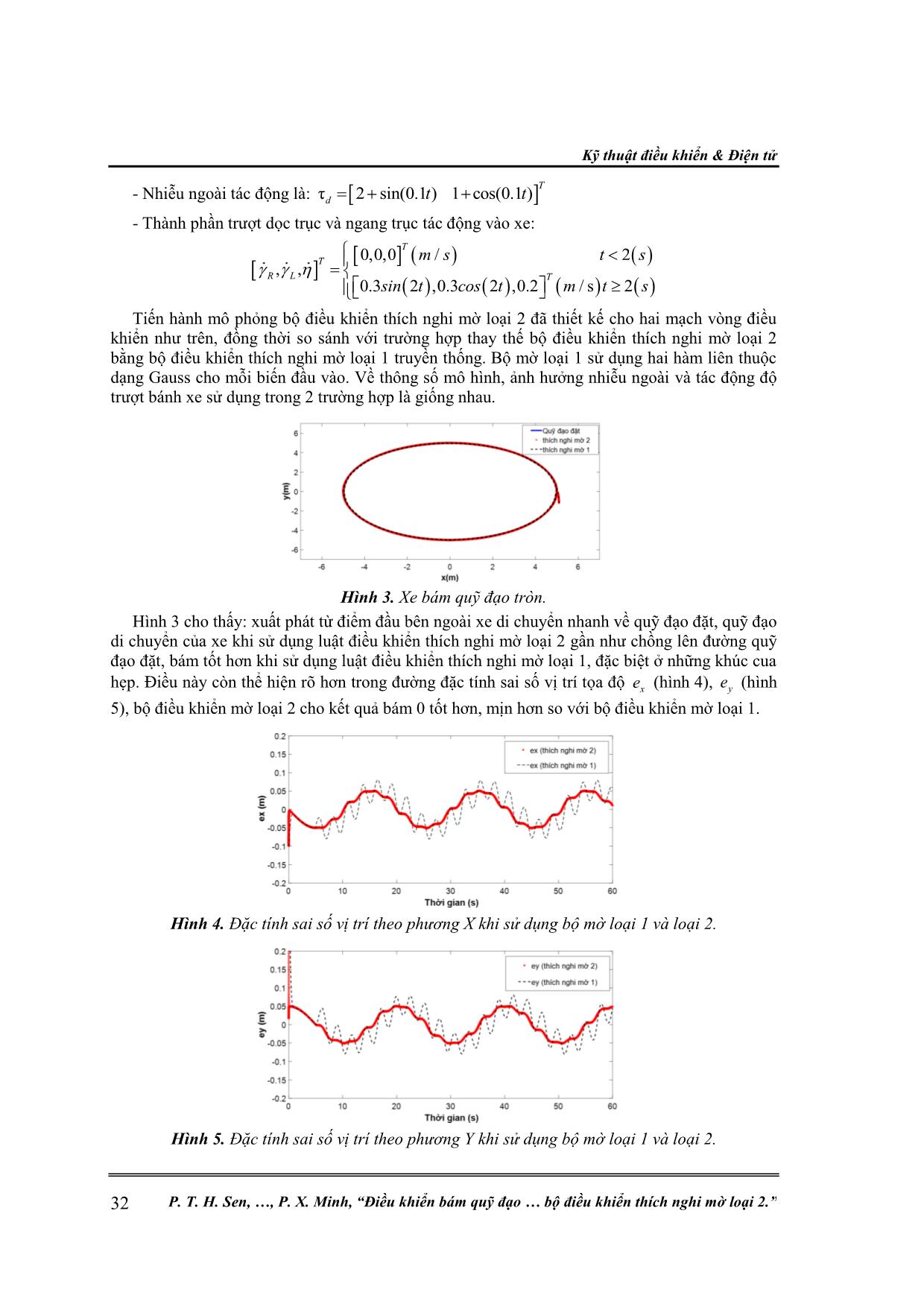
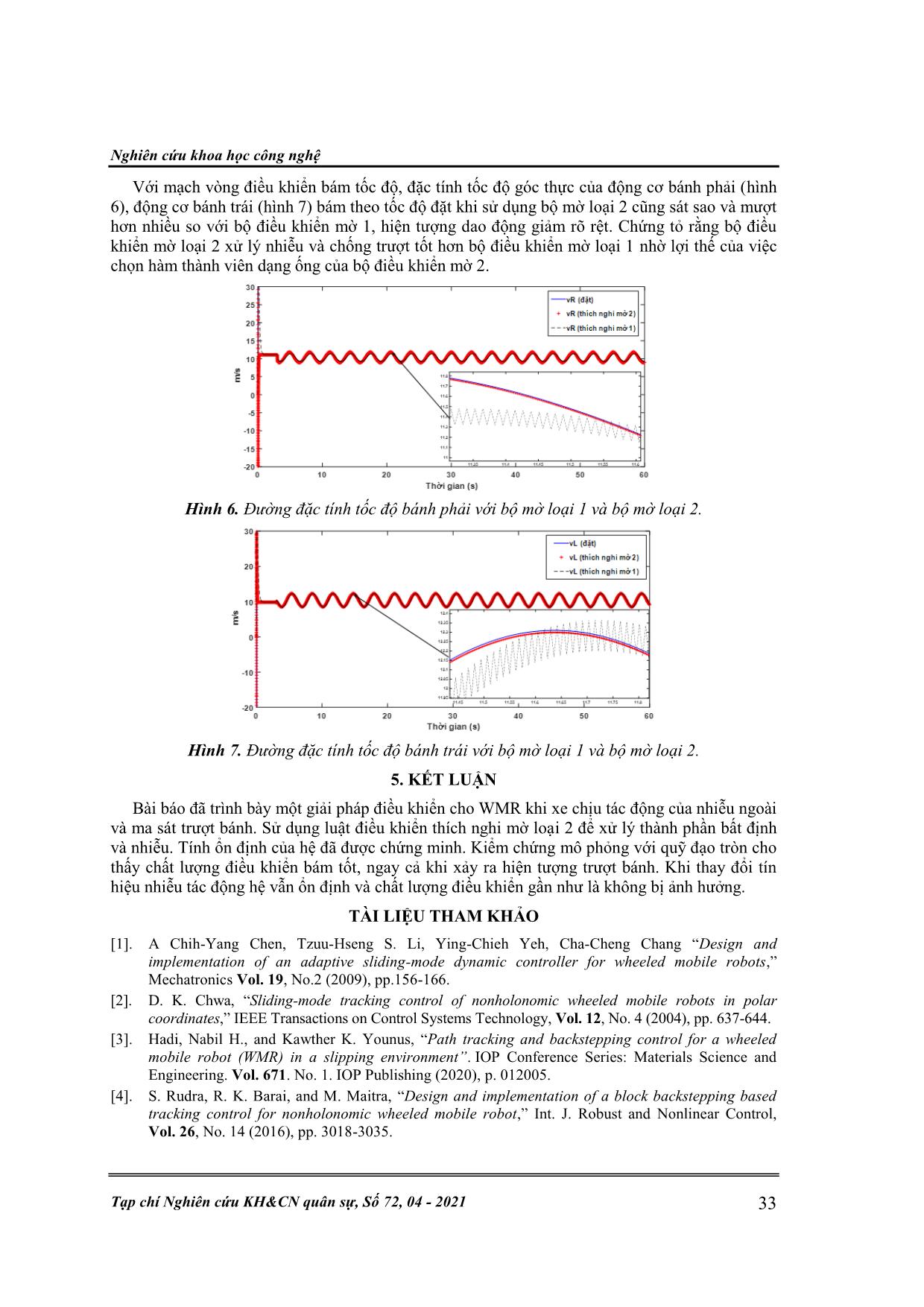
Kỹ thuật điều khiển & Điện tử 
 24 P. T. H. Sen, , P. X. Minh, “Điều khiển bám quỹ đạo  bộ điều khiển thích nghi mờ loại 2.” 
ĐIỀU KHIỂN BÁM QUỸ ĐẠO CHO XE TỰ HÀNH 
SỬ DỤNG BỘ ĐIỀU KHIỂN THÍCH NGHI MỜ LOẠI 2 
Phạm Thị Hương Sen1, 2, Hà Quốc Việt1, Vũ Thị Thúy Nga
1*
,
Phan Xuân Minh
1
Tóm tắt: Bài báo đề xuất thuật toán điều khiển mờ loại 2 kết hợp với thích nghi cho xe 
tự hành để xử lý ma sát trượt và nhiễu ngoài. Cấu trúc điều khiển bao gồm hai mạch vòng 
động học và động lực học, tính ổn định cho từng mạch vòng điều khiển được chứng minh 
dựa trên tiêu chuẩn Lyapunov. Bộ điều khiển được kiểm chứng bằng mô phỏng số trên nền 
Matlab- Simulink. Các kết quả mô phỏng cho thấy, hệ ổn định và có chất lượng bám tốt 
ngay cả khi tồn tại ma sát trượt và nhiễu không biết trước. 
Từ khóa: Mờ loại 2; Điều khiển thích nghi; Xe tự hành; Trượt bánh. 
1. GIỚI THIỆU CHUNG 
Xe tự hành (Wheeled Mobile Robot -WMR) là loại robot tự hành với kết cấu ba bánh đơn 
giản, có khả năng duy trì cân bằng tốt. WMR được ứng dụng rộng rãi trong nhiều lĩnh vực như 
hàng không, vũ trụ, các thiết bị vận chuyển dưới nước, sử dụng thay cho con người trong môi 
trường độc hại hoặc vận chuyển hàng hóa, tìm kiếm vật liệu cháy nổ. Điều khiển xe tự hành bám 
quỹ đạo vẫn luôn thu hút được sự quan tâm của các nhà nghiên cứu khoa học, từ việc xây dựng 
mô hình động học xe đến việc thiết kế điều khiển. Nhiều phương pháp điều khiển đã được đề 
xuất như điều khiển trượt [1, 2]; điều khiển Backstepping [3, 4]; điều khiển thích nghi [5, 6], 
điều khiển thích nghi mờ [7]. 
Tuy nhiên, những phương pháp đã được công bố thường chỉ quan tâm đến bù sai lệch mô 
hình, nhiễu hằng hoặc một số hàm bất định trong mô hình mà chưa xem xét đến ma sát trượt 
bánh, loại ma sát thường xuất hiện ở các loại WMR. Trên thực tế, khi vận hành xe di chuyển vào 
những khúc cua hoặc khi di chuyển với tốc độ cao, trên mặt sàn trơn, có vật cản, sẽ xảy ra hiện 
tượng trượt bánh xe, ảnh hưởng đến tốc độ và vị trí của xe. Để khắc phục ảnh hưởng ma sát trượt 
có thể thực hiện bằng cách bù trực tiếp thông qua các thiết bị đo vận tốc và gia tốc trượt, hoặc bù 
gián tiếp. Gần đây, giải pháp bù gián tiếp qua bộ điều khiển đã có một số kết quả nghiên cứu 
công bố: như sử dụng bộ ước lượng nhiễu để ước lượng và bù ma sát trượt bánh [9]. Trong [10, 
11], thành phần bất định, nhiễu và ma sát trượt bánh được ước lượng và bù dựa trên mạng nơ ron 
nhân tạo. Cho lớp mô hình hệ phi tuyến đa biến bất định thì theo nhóm tác giả Lin, Liu, Kuo hệ 
logic mờ luôn là công cụ thiết kế bộ điều khiển đơn giản và hiệu quả [12]. Sau đó, những nghiên 
cứu trong [13] đã kế thừa và phát triển bộ điều khiển thích nghi mờ nhằm nâng cao hiệu quả điều 
khiển cho một lớp hệ bất định, chịu nhiễu tác động không biết trước. 
Với ảnh hưởng của hiện tượng ma sát trượt bánh xe và các thành phần nhiễu ngoài tác động 
không biết trước, nhóm tác giả đề xuất sử dụng hệ logic mờ loại 2 để thiết kế bộ điều khiển cho 
WMR, kết hợp với điều khiển thích nghi để chỉnh định tham số đầu ra của bộ mờ. Hơn nữa, để 
giảm ảnh hưởng sai số xấp xỉ của bộ mờ và nhiễu ngoài thì thành phần điều khiển bền vững H 
được thêm vào trong bộ điều khiển mạch vòng động lực học xe tự hành. Nội dung bài báo được 
trình bày trong 4 phần: giới thiệu chung, mô hình của WMR ba bánh, tổng hợp bộ điều khiển và 
phần cuối là mô phỏng kiểm chứng. 
2. MÔ HÌNH ĐỘNG HỌC ĐỘNG LỰC HỌC 
 2.1. Mô hình động học 
Xét cơ cấu xe tự hành ba bánh, hai bánh đẩy phía sau và một bánh lái phía trước, được biểu 
diễn trong hình 1a. Với G là trọng tâm xe, M là điểm nằm giữa trục nối hai bánh sau có tọa độ 
( , )M Mx y ,  là góc hướng của xe. Gọi 1F và 2F là lực dọc trục ở bánh xe bên phải và bên trái, 
3F là tổng lực ma sát dọc trục bánh xe. Khoảng cách giữa hai bánh sau là 2b, r là bán kính của 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 25 
mỗi bánh xe. 
a. 
b. 
Hình 1. a. Mô hình xe tự hành; 
b. Mô hình xe gắn trên tọa độ M bám mục tiêu Z. 
Vận tốc góc của động cơ bánh xe phải, trái lần lượt là R , L . Gọi R , L là độ trượt dọc trục 
của bánh xe bên phải và bên trái, η là độ trượt ngang trục bánh xe. Vận tốc tuyến tính theo hướng 
vuông góc với trục nối hai bánh sau và vận tốc quay của xe là [11]: 
2 2
R L R L
r     
 (1) 
2 2 2
R L R L R L
r
b b b
     
 
 (2) 
Phương trình chuyển động của xe khi có xét đến hiện tượng trượt bánh: 
cos sin
sin cos
G
G
x
y
  
  
 
  
  
 (3) 
Và điều kiện ràng buộc nonholonomic khi có xét đến hiện tượng trượt bánh xe: 
cos sin
cos sin
sin cos
R R
L L
r x y b
r x y b
x y
    
    
  
 (4) 
2.2. Mô hình động lực học 
Xét cơ cấu xe tự hành xe di chuyển trên mặt sàn ngang, trọng tâm khối lượng xe trùng với 
trọng tâm hình học xe. Mô hình động lực học của xe tự hành được mô tả theo phương trình 
Lagrange [11]: 
 dv (v)v v γ τ τM B E Q C G  (5) 
nhân cả 2 vế (5) với -1M ... nh tính ổn định: 
Giả thiết 1: Giả sử D bị chặn, tồn tại một hằng số 
0d sao cho 
2
0δ δ
T d . 
Chọn hàm Lyapunov: 
 1 1 1
1 1
e e
2 2
T T
v vV P 

 (20) 
Lấy đạo hàm cấp 1 theo thời gian: 
 1 1 11 1 1 1 1 1
1
δ
1 1 1 1
e e e e e ξ
2
e
2 2
δeT T T T T Tv v v v v v v
T TB P PV P P PBB G  
 
 (21) 
Thay (15), (17) vào (21) và biến đổi ta có: 
2
1 1 1 1
1 1 1 1 1
e e δ δ e δ e δ
2 2 2
T
T T T T
v v v vV Q PB PB  
 
2
1 1
1 1
e e δ δ
2 2
T T
v vV Q  (22) 
Lấy tích phân hai vế phương trình (22) trong khoảng [0, T]: 
2
1 1 1
0 0
1 1
( ) (0) e e δ δ
2 2
T T
T T
v vV T V Q dt dt 
Theo giả thiết 1 ta có 2 2 0δ d và 1( ) 0V T , nên: 
2 2
1 1 1 1
0 0 0 0
1 1 1 1
(0) e e δ δ e e (0) δ δ
2 2 2 2
T T T T
T T T T
v v v vV Q dt dt Q dt V dt  
Kỹ thuật điều khiển & Điện tử 
 28 P. T. H. Sen, , P. X. Minh, “Điều khiển bám quỹ đạo  bộ điều khiển thích nghi mờ loại 2.” 
2
1 1 1
0 0
1 1 1 1
e e δ δ e (0) e (0) (0) (0)
2 2 2 2
T T
T T T T
v v v vQ dt dt P 

Như vậy, hệ thống đảm bảo tính ổn định bền vững với hệ số suy giảm  . 
3.2. Tổng hợp bộ điều khiển mạch vòng động học 
Điều khiển xe tự hành bám theo một quỹ đạo cho trước, gọi điểm mục tiêu di chuyển của xe 
là ( , )Z ZZ x y , sai lệch vị trí giữa điểm giữa hai bánh xe (điểm M) với điểm mục tiêu Z trên hệ tọa 
độ OXY như hình 1b là: 
cos sin
e
sin cos
x Z M
p
y Z M
e x x
e y y
 
 
 (23) 
Lấy đạo hàm cấp một của phương trình (23): 
cos sin cos sin
e
sin cos sin cos
yZ M
p
xZ M
ex x
ey y
   

   
 (24) 
Thay các phương trình số (1), (2), (3) vào (24) và rút gọn ta có: 
cos sin
e hu d
sin cos
x Z
p p
y Z
e x
e y
 
 
 (25) 
1 1
2 2
h
2 2
y y
x x
e er r
b b
e r e r
b b
; 
2 2
d
2
R L R L
y
R L
x
e
b
e
b
   
 

; u Rp
L


Luật điều khiển u p cho (25) sẽ được tách thành hai thành phần 1u p và 2u p , trong đó, 1u p là 
tín hiệu bù nhiễu cho thành phần phi tuyến trong mô hình, 2u p là tín hiệu điều khiển phản hồi: 
 1 2u u up p p (26) 
Chọn: 
1
1
cos sin
u h
sin cos
Z
p
Z
x
y
 
 
 (27) 
 Thay (26), (27) vào (25) được: 
 2e hu dp p (28) 
Khi nhiễu loạn bên ngoài d 0 thì ta đề xuất luật điều khiển 2u p là: 
* 1
2 2 2u u h ep p pK
 (29) 
Với 
2K là xác định dương. 
Thay (29) vào phương trình (28), ta dễ dàng có được: 2e e 0p pK và lime 0p
t
t
 . 
Tuy nhiên, khi xét đến thành phần nhiễu thì luật điều khiển như (29) không còn chính xác. Do 
đó, nhóm tác giả đề xuất sử dụng bộ điều khiển thích nghi mờ loại 2 cho tín hiệu điều khiển 2u p 
như sau: 
1
2 2 2 1 2
0
ˆu u (e | ) h ( e e u )
t
p p p p p kdt 
   (30) 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 29 
Trong đó, 
1 , 2 là các hằng số xác định dương; 2 2uˆ (e | )p p là đầu ra của bộ điều khiển 
thích nghi mờ loại 2: 
 2 2 2 2uˆ (e | ) ζ
T
p p (31) 
Với 2 2ξ (ξ )pdiag , 2 21 22 2 2ξ , ,... ,...,p j    , 2 j được tính theo công thức [15]: 
2
2
2
1
j
j
j
j
f
f


(32) 
 1 jf là độ thoả mãn mệnh đề điều kiện thứ j. Thay (30), (31) vào (28), ta có: 
 * *1 2 2 2 2 2
0
ˆe e e h u (e | ) u hu u d
t
p p p p p p p kdt   (33) 
Thay (29) vào và đặt 
1 2K  , ta có: 
 *2 2 2 2 2 2 2 2 k
0
ˆe e e h u (e | ) u d u
t
p p p p p pdt B B B   (34) 
Với 
2B là ma trận đơn vị,  1 2d
T
d d là nhiễu. 
Gọi 
minw là sai số ước lượng nhỏ nhất: 
 * *min 2 2ˆw h u (e | ) up p p (35) 
Thay (35) vào (34) và rút gọn ta có: 
 2 2 2 2 2
0
e e e hξ (σ u )
t
T
p p p kdt B B   (36) 
Với *2 2 2 , minσ d w . 
Đề xuất tín hiệu điều khiển uk và luật thích nghi 2 như sau: 
 22
1
u eTk pB
 (37) 
 2 2 2ξ h eT pB (38) 
Giả thiết 2: Với  2 0, , (0, )L T T , tồn tại một hằng số 0c sao cho: 
2
0.
T c   
Chọn hàm Lyapunov: 
2 2 2 2
0 0
1 1 1
e e e e
2 2 2
T
t t
T T
p p p pV dt dt 
  
 (39) 
Lấy đạo hàm cấp một của 
2V theo thời gian: 
2 2 2 2 2
0 0
1 1 1 1
e e e e e e e e
2 2 2 2
T
t t
T T T T
p p p p p p p pV dt dt 
   
 (40) 
Thay (36) vào (40) và rút gọn ta có: 
Kỹ thuật điều khiển & Điện tử 
 30 P. T. H. Sen, , P. X. Minh, “Điều khiển bám quỹ đạo  bộ điều khiển thích nghi mờ loại 2.” 
 2 2 2 2 2 2 2 2 22 2
1 1 1
e e σ e e e σ e e hξ
2
T
T T T T T T T T
p p p p p p pV B B B B B 
  
 (41) 
Chọn luật điều khiển như (37), (38) thì từ (41), ta có: 
2
2 2 2 2 22
1 1 1 1 1
e e e σ e σ σ σ
2 2 2
T
T T T T T
p p p pV N B B B B 
Khi đó: 22 2
1
e e σ σ
2
T T
p pV Q ; với 2 2 22
1
2
TQ B B
  (42)
Lấy tích phân hai vế phương trình (42) trong khoảng [0,T] ta có: 
2
2 2 2
0 0
1
( ) (0) e e σ σ
2
T T
T T
p pV T V Q dt dt (43) 
Theo giả thiết 2 thì 2 2 0σ c , mà 2 0V T , do đó, 2
0
e e
T
T
p pQ dt bị chặn trong khoảng 
 0,T và tất cả các biến trong 2V bị chặn nên 2V cũng bị chặn. Tuy nhiên, các kết luận trên vẫn 
chưa đảm bảo e 0p , do đó, cần sử dụng thêm bổ đề Barbalat để chứng minh tính hội tụ về 0 
của biến sai lệch e p . 
Định nghĩa thêm một hàm 0 (e , )pV t như sau: 0 2e e
T
p pV Q và 0 22e e
T
p pV Q 
Ta có 2 2e ,h,ξ ,p là bị chặn, σ là hữu hạn, do đó, e p là bị chặn và 0V cũng bị chặn. Theo bổ 
đề Barbalat thì 0 (e , ) 0pV t khi t , tức là e 0p , điều này chứng tỏ với luật điều khiển 
trong (30) thì vec tơ biến sai lệch trong (23) là hội tụ về 0, đảm bảo tính ổn định. 
Hình 2. Sơ đồ khối cấu trúc hệ thống điều khiển hai mạch vòng. 
Lưu ý: khi xe đã bám quỹ đạo đặt thì các sai lệch 
xe và ye sẽ về không. Điều này làm cho 
2
det(h) 0
2
x
r
e
b
 , nên h không nghịch đảo được. Để tránh hiện tượng này, thành phần điều 
khiển 1u p , 2u p trong công thức (27), (30) được chọn như sau: 
1
1
cos sin
h
sin cos
u
cos sin1
sin cos
Z
x
Z
p
Z
x
Z
x
khi e
y
x
khi e
y
 

 
 

 
 (44) 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 31 
1
2 2 1 2
0
2
2 2 1 2
0
uˆ (e | ) h ( e e u )
u
1
uˆ (e | ) ( e e u )
t
p p p p k x
p t
p p p p k x
dt khi e
dt khi e
 
 

   
   
 (45) 
Với  có giá trị đủ nhỏ. 
4. KẾT QUẢ MÔ PHỎNG 
Tham số xe tự hành được sử dụng trong bài báo: 
10Gm kg , w 2m kg ,
2
w 0.1I kgm , 
20.05DI kgm 
24 , 0.3 , 0.15 , 0.2GI kgm b m r m a m 
Các hệ số: 
1 22, 3  , 
20.02, 0.0001p p . Chọn ma trận hệ số: 
1
30 0
0 30
Q
,
6,5678 0
0 6,5678
P
, 
1 2
1 0
0 1
K K
 Các lựa chọn cho bộ mờ loại 2: 
- Hàm liên thuộc dạng hình thang cho biến đầu vào sai lệch ,x ye e là 1 2,X X và ,R Lv ve e là 
1 2,V V như sau: 
11
11
1
12
12
1,5 1,5 0,5 1,5 1
1,5 1,5 1,5 0,5 1
,
1,5 1,5 0,5 1,5 1
0,5 0,5 0,5 1,5 1
u
l
u
l
X
X
X
X
X
21
21
2
22
22
3 3 1 3 1
3 3 1 3 1
,
3 3 1 3 1
1 1 3 3 1
u
l
u
l
X
X
X
X
X
11
11
1
12
12
9 9 3 1
9 9 9 1
,
9
9
1
3
9
3
3 9
1
9
9 9
u
l
l
l
V
V
V
V
V
21
21
2
22
22
15 15 7.5 15 1
15 15 15 7.5 1
15 7.5 15 15 1
7.5 15 15 15 1
u
l
u
l
V
V
V
V
V
Bảng 1. Hàm liên thuộc biến đầu ra Y, Z. 
1x 2x 21X 22X 1v 2v 21V 22V 
11X  
1 1, 0.9Y  2 0.6, 0.4Y 11V  
1 1, 0.8Z  2 0.6, 0.4Z 
12X  
3 0.4,0.6Y  4 0.9,1Y 12V  
3 0.4,0.6Z  4 0.8,1Z 
- Luật điều khiển mờ chọn giống như trong [14] 
 Kiểm chứng thuật toán, mô phỏng với quỹ đạo đặt: 5cos 0.1 , 5sin 0.1Z Zx t y t 
- Chọn điều kiện đầu của hệ:  110 1, 0 1, 0 25, 25, 25, 25 ,R Lref ref   
      21 21 22 0 25, 25, 25, 25 , 0 10,1 0,1 0,1 0 , 0 10,1 0,1 0,1 0 
- Vị trí và góc hướng ban đầu của xe:   1(0) (0), , (0) 5, , 
2
M Mx y

Kỹ thuật điều khiển & Điện tử 
 32 P. T. H. Sen, , P. X. Minh, “Điều khiển bám quỹ đạo  bộ điều khiển thích nghi mờ loại 2.” 
- Nhiễu ngoài tác động là:  τ 2 sin(0.1 ) 1 cos(0.1 )
T
d t t 
- Thành phần trượt dọc trục và ngang trục tác động vào xe: 
 
  
0, 0, 0 / 2
, , 
0.3 2 , 0.3 2 , 0.2 / s 2
T
T
R L T
m s t s
sin t scos t m t
  
Tiến hành mô phỏng bộ điều khiển thích nghi mờ loại 2 đã thiết kế cho hai mạch vòng điều 
khiển như trên, đồng thời so sánh với trường hợp thay thế bộ điều khiển thích nghi mờ loại 2 
bằng bộ điều khiển thích nghi mờ loại 1 truyền thống. Bộ mờ loại 1 sử dụng hai hàm liên thuộc 
dạng Gauss cho mỗi biến đầu vào. Về thông số mô hình, ảnh hưởng nhiễu ngoài và tác động độ 
trượt bánh xe sử dụng trong 2 trường hợp là giống nhau. 
Hình 3. Xe bám quỹ đạo tròn. 
Hình 3 cho thấy: xuất phát từ điểm đầu bên ngoài xe di chuyển nhanh về quỹ đạo đặt, quỹ đạo 
di chuyển của xe khi sử dụng luật điều khiển thích nghi mờ loại 2 gần như chồng lên đường quỹ 
đạo đặt, bám tốt hơn khi sử dụng luật điều khiển thích nghi mờ loại 1, đặc biệt ở những khúc cua 
hẹp. Điều này còn thể hiện rõ hơn trong đường đặc tính sai số vị trí tọa độ 
xe (hình 4), ye (hình 
5), bộ điều khiển mờ loại 2 cho kết quả bám 0 tốt hơn, mịn hơn so với bộ điều khiển mờ loại 1. 
Hình 4. Đặc tính sai số vị trí theo phương X khi sử dụng bộ mờ loại 1 và loại 2. 
Hình 5. Đặc tính sai số vị trí theo phương Y khi sử dụng bộ mờ loại 1 và loại 2. 
Nghiên cứu khoa học công nghệ 
 Tạp chí Nghiên cứu KH&CN quân sự, Số 72, 04 - 2021 33 
Với mạch vòng điều khiển bám tốc độ, đặc tính tốc độ góc thực của động cơ bánh phải (hình 
6), động cơ bánh trái (hình 7) bám theo tốc độ đặt khi sử dụng bộ mờ loại 2 cũng sát sao và mượt 
hơn nhiều so với bộ điều khiển mờ 1, hiện tượng dao động giảm rõ rệt. Chứng tỏ rằng bộ điều 
khiển mờ loại 2 xử lý nhiễu và chống trượt tốt hơn bộ điều khiển mờ loại 1 nhờ lợi thế của việc 
chọn hàm thành viên dạng ống của bộ điều khiển mờ 2. 
Hình 6. Đường đặc tính tốc độ bánh phải với bộ mờ loại 1 và bộ mờ loại 2. 
Hình 7. Đường đặc tính tốc độ bánh trái với bộ mờ loại 1 và bộ mờ loại 2. 
5. KẾT LUẬN 
Bài báo đã trình bày một giải pháp điều khiển cho WMR khi xe chịu tác động của nhiễu ngoài 
và ma sát trượt bánh. Sử dụng luật điều khiển thích nghi mờ loại 2 để xử lý thành phần bất định 
và nhiễu. Tính ổn định của hệ đã được chứng minh. Kiểm chứng mô phỏng với quỹ đạo tròn cho 
thấy chất lượng điều khiển bám tốt, ngay cả khi xảy ra hiện tượng trượt bánh. Khi thay đổi tín 
hiệu nhiễu tác động hệ vẫn ổn định và chất lượng điều khiển gần như là không bị ảnh hưởng. 
TÀI LIỆU THAM KHẢO 
[1]. A Chih-Yang Chen, Tzuu-Hseng S. Li, Ying-Chieh Yeh, Cha-Cheng Chang “Design and 
implementation of an adaptive sliding-mode dynamic controller for wheeled mobile robots,” 
Mechatronics Vol. 19, No.2 (2009), pp.156-166. 
[2]. D. K. Chwa, “Sliding-mode tracking control of nonholonomic wheeled mobile robots in polar 
coordinates,” IEEE Transactions on Control Systems Technology, Vol. 12, No. 4 (2004), pp. 637-644. 
[3]. Hadi, Nabil H., and Kawther K. Younus, “Path tracking and backstepping control for a wheeled 
mobile robot (WMR) in a slipping environment”. IOP Conference Series: Materials Science and 
Engineering. Vol. 671. No. 1. IOP Publishing (2020), p. 012005. 
[4]. S. Rudra, R. K. Barai, and M. Maitra, “Design and implementation of a block backstepping based 
tracking control for nonholonomic wheeled mobile robot,” Int. J. Robust and Nonlinear Control, 
Vol. 26, No. 14 (2016), pp. 3018-3035. 
Kỹ thuật điều khiển & Điện tử 
 34 P. T. H. Sen, , P. X. Minh, “Điều khiển bám quỹ đạo  bộ điều khiển thích nghi mờ loại 2.” 
[5]. Koubaa, Yasmine, Mohamed Boukattaya, and Tarak Dammak, “Adaptive control of nonholonomic 
wheeled mobile robot with unknown parameters,” 2015 7th International Conference on Modelling, 
Identification and Control (ICMIC), IEEE (2015), pp.1-5. 
[6]. Xin, L., Wang, Q., She, J., & Li, Y., “Robust adaptive tracking control of wheeled mobile 
robot,” Robotics and Autonomous Systems, Vol 78 (2016), pp. 36-48. 
[7]. Das, Tamoghna, and Indra Narayan Kar, “Design and implementation of an adaptive fuzzy logic-
based controller for wheeled mobile robots,” IEEE Transactions on Control Systems 
Technology 14.3 (2006), pp. 501-510. 
[8]. Y. Jinhua, Y. Suzhen, & J. Xiao, “Trajectory Tracking Control of WMR Based on Sliding Mode 
Disturbance Observer with Unknown Skidding and Slipping,” 2nd International Conference on 
Cybernetics, Robotics and Control (CRC), IEEE (2017), pp. 18-22. 
[9]. Phạm Thị Hương Sen, Vũ Thị Thúy Nga, Phan Xuân Minh , “ Điều khiển thích nghi bám quỹ đạo cho xe 
tự hành dựa trên bộ ước lượng nhiễu,” Tạp chí Nghiên cứu KH&CN quân sự, số 64, 12-2019, pp. 40-51. 
[10]. NGUYEN, T., & LE, L., “Neural network-based adaptive tracking control for a nonholonomic 
wheeled mobile robot with unknown wheel slips, model uncertainties, and unknown bounded 
disturbances,” TURKISH JOURNAL OF ELECTRICAL ENGINEERING & COMPUTER 
SCIENCES, Vol. 26, No. 1 (2018), pp. 378-392. 
[11]. Nguyen, Tinh, et al., “A Gaussian wavelet network-based robust adaptive tracking controller for a 
wheeled mobile robot with unknown wheel slips,” International Journal of Control 92.11 (2019), pp. 
2681-2692. 
[12]. Lin, Tsung-Chih, Han-Leih Liu, and Ming-Jen Kuo, “Direct adaptive interval type-2 fuzzy control of 
multivariable nonlinear systems,” Engineering Applications of Artificial Intelligence 22.3 (2009), 
pp. 420-430. 
[13]. Ghaemi, Mostafa, Seyyed Kamal Hosseini-Sani, and Mohammad Hassan Khooban, “Direct adaptive 
general type-2 fuzzy control for a class of uncertain non-linear systems,” IET Science, Measurement 
& Technology 8.6 (2014), pp. 518-527. 
[14]. Shaocheng, Tong, Chen Bin, and Wang Yongfu, “Fuzzy adaptive output feedback control for MIMO 
nonlinear systems,” Fuzzy Sets and Systems 156.2 (2005), pp. 285-299. 
[15]. Zhou, Hai-bo, Hao Ying, and Ji-an Duan. "Adaptive control using interval Type-2 fuzzy logic for 
uncertain nonlinear systems," Journal of Central South University of Technology 18.3 (2011): 760. 
[16]. Wu, Dongrui, “A brief Tutorial on Interval type-2 fuzzy sets and systems,” (2010), Fuzzy sets and 
systems. 
[17]. Klancar, Gregor, et al. “Wheeled mobile robotics: from fundamentals towards autonomous systems,” 
(2017), Butterworth-Heinemann. 
ABSTRACT 
TYPE-2 FUZZY ADAPTIVE TRAJECTORY TRACKING OF WHEELED MOBILE ROBOT 
This paper proposes a type 2 -fuzzy adaptive control tracking for wheeled mobile 
robots with wheel slip. We use the adaptive interval type-2 fuzzy logic controller to 
approximate the optimal control law for both kinematic and dynamics loops under the 
conditions that the wheels of the wheel mobile robot slip. The stability of the overall 
system is proof using Lyapunov stability. The proposed control schema is simulated by 
Matlab-Simulink, the results show that the system is stable and the position tracking 
errors converge to zero. 
Keywords: Type-2 fuzzy; Adaptive control; Wheeled mobile robot; Wheel slip. 
Nhận bài ngày 20 tháng 9 năm 2020 
Hoàn thiện ngày 20 tháng 12 năm 2020 
Chấp nhận đăng ngày 12 tháng 4 năm 2021 
Địa chỉ: 1 Đại học Bách khoa Hà Nội; 
2
 Đại học Điện lực. 
*
 Email: nga.vuthithuy@hust.edu.vn.