Data balancing methods by fuzzy rough sets
Abstract: The robustness of rough sets theory in data cleansing have been proved in
many studies. Recently, fuzzy rough set also make a deal with imbalanced data by two
approaches. The first is a combination of fuzzy rough instance selection and balancing
methods. The second tries to use different criteria to clean majorities and minorities
classes of imbalanced data. This work is an extension of the second method which was
presented in [16]. The paper depicts complete study about the second method with some
proposed algorithms. It focuses mainly on binary classification with kNN and SVM for
imbalanced data. Experiments and comparisons among related methods will confirm pros
and coin of each method with respect to performance accuracy and time consumption.

Trang 1

Trang 2

Trang 3

Trang 4
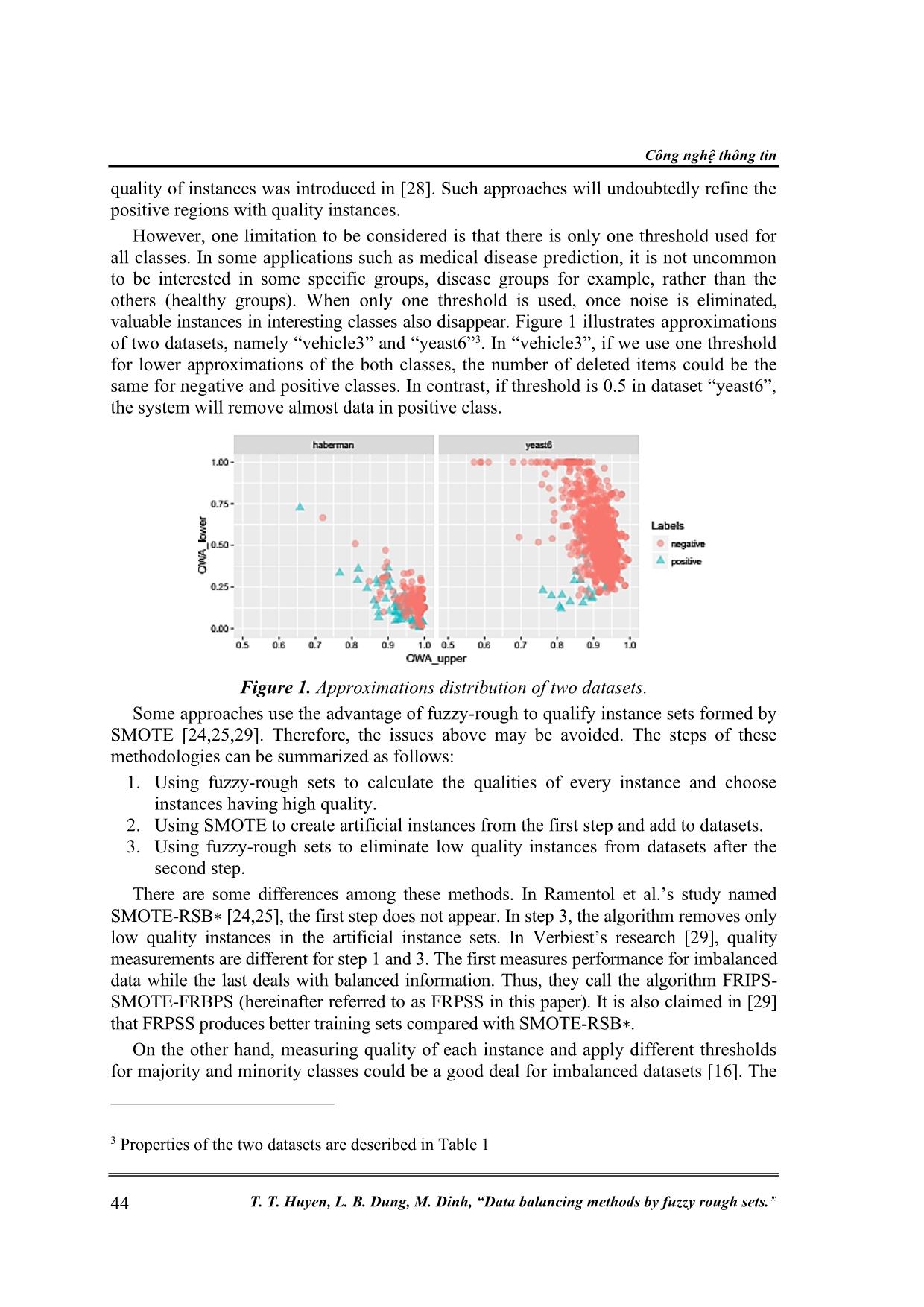
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
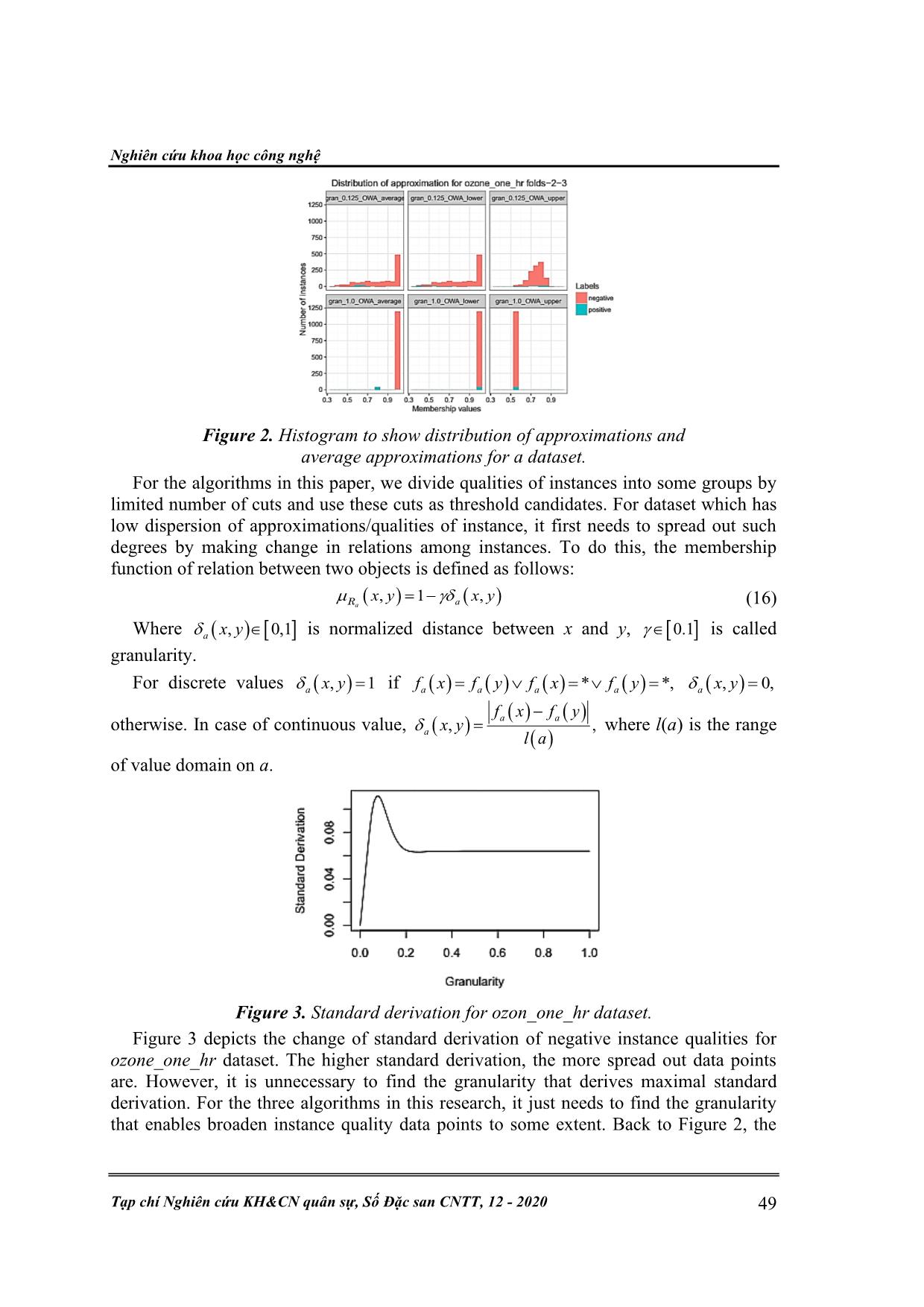
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Data balancing methods by fuzzy rough sets

Công nghệ thông tin 40 T. T. Huyen, L. B. Dung, M. Dinh, “Data balancing methods by fuzzy rough sets.” DATA BALANCING METHODS BY FUZZY ROUGH SETS Tran Thanh Huyen1,2*, Le Ba Dung3, Mai Dinh4 Abstract: The robustness of rough sets theory in data cleansing have been proved in many studies. Recently, fuzzy rough set also make a deal with imbalanced data by two approaches. The first is a combination of fuzzy rough instance selection and balancing methods. The second tries to use different criteria to clean majorities and minorities classes of imbalanced data. This work is an extension of the second method which was presented in [16]. The paper depicts complete study about the second method with some proposed algorithms. It focuses mainly on binary classification with kNN and SVM for imbalanced data. Experiments and comparisons among related methods will confirm pros and coin of each method with respect to performance accuracy and time consumption. Keywords: Rough Set theory; Fuzzy-rough sets; Granular computing; Imbalanced data; Instance selection. 1. INTRODUCTION Rough set theory was first introduced by Pawlak [21, 22] in early 1980s as a machine learning methods for knowledge acquisition from data. It provides mathematical approach to deal with inconsistency between items in datasets. It consequently can be used for pattern extraction, decision rule generation, feature selection and data reduction. In case of data reduction/selection, main ideas are extracting fuzzy memberships of positive regions [23] and choosing the instances which have large membership degrees (degrees have to larger than thresholds) for training phases [3, 13, 28]. It thus can reduce noise by defining and eliminating low quality instances in balance datasets. Other issue that may cause an inconsistency problem is imbalanced data [15]. A dataset is imbalanced when the numbers of instances in some classes are much larger than in others. Such classes are called majority classes. The classes with small cardinality are referred to as minority classes. There are two possible approaches in using fuzzy rough set [23] to select instance from imbalanced datasets. The first is combination of balancing methods and a rough set based noise removed technique [24, 25, 29]. In these approaches, fuzzy rough sets are first used to remove low quality instances. Then, a well-known balancing technique called “Synthetic Minority Oversampling Technique (SMOTE)” [4] is employed to form a candidate set. Finally, fuzzy-rough sets are used again to select quality instances from the candidate sets. The second approach is using different criteria in defining different thresholds for majority and minority classes [16, 27]. By using small threshold for minority class, more items from minority classes can be selected. Besides, the research in [16] introduces other method to deal with highly imbalanced data by keeping all instance in minority class while remove/change label in majority class. The experimental results in those studies show considerable improvement in classification performance. However, the absence of generating candidates and optimizing thresholds methods limits application in real. There are also some study in using fuzzy-rough sets as classification methods for imbalanced data [26, 30]. However, making a classifier is not in scope of this paper. This research will show complete study of using fuzzy rough set to select instance in Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 41 imbalanced dataset without any balancing techniques. The paper is structured as follows: Section 2 reviews the original rough set theory and an extension called fuzzy-rough set; In section 3, fuzzy rough instance selection approach to deal with inconsistency is discussed along with their issues; The proposed algorithms of this research with methods to choose parameters are introduced in section 4; Experiments with results and comparisons are discussed in section 5; Finally, section 6 concludes the study. 2. THEORETICAL BACKGROUND 2.1. Information Systems and Tolerance Relation An information system is represented as a data table. Each row of this table represents an instance of an object such as people, things, etc. Information about every object is described by object attribute (feature) values. An information system in the rough sets study is formally defined as a pair ( ),I U A= where U is a non-empty finite set of objects called the universe and A is a non-empty finite set of attributes such that :af U A→ for every a A [21, 22]. The non-empty discrete value set Va is called the domain of a. The original rough set theory deals with complete information systems in which ( ), , ax U a A f x is a precise value. If U contains at least an unknown value object, then I is called an incomplete information system, ... 5.46 0.7463 0.5583 0.7258 0.7889 0.6825 0.7239 abalone9-18 16.40 0.5119 0.5060 0.5978 0.6153 0.5256 0.5256 yeast-1-4-5-8 vs 7 22.10 0.5000 0.5000 0.5848 0.6197 0.5735 0.5282 glass5 22.78 0.5000 0.5000 0.6711 0.7014 0.6931 0.7123 kr-vs-k- one_vs_fifteen 27.77 0.9647 0.9647 0.9799 0.9647 0.9679 0.9808 yeast4 28.10 0.5333 0.5294 0.7618 0.7643 0.7539 0.8020 winequality-red-4 29.17 0.5000 0.5000 0.5498 0.5861 0.6081 0.6043 yeast-1-2-8-9 vs 7 30.57 0.5000 0.5000 0.5684 0.6764 0.5959 0.6458 ozone one hr 31.42 0.5000 0.5000 0.7231 0.6696 0.7411 0.7413 yeast5 32.73 0.7044 0.7103 0.8774 0.9391 0.8755 0.8888 winequality-red-8 vs 6.csv 35.44 0.5000 0.5000 0.5632 0.5618 0.6616 0.6609 ecoli-0-1-3-7_vs_2- 6 39.00 0.6667 0.5000 0.5000 0.6667 0.6740 0.6479 yeast6 41.40 0.6440 0.6599 0.8247 0.8644 0.7649 0.8821 winequality-red-8 vs 6-7 46.50 0.5000 0.5000 0.4754 0.5320 0.6465 0.6465 abalone-19_vs_10- 11-12-13 49.69 0.5000 0.5000 NA 0.5431 0.5674 0.5716 shuttle-2 vs 5 66.67 0.9841 0.9486 0.9524 0.9789 0.9841 0.9841 winequality-red-3 vs 5 68.10 0.5000 NA NA 0.5412 0.5725 0.5718 poker-8-9 vs 5.csv 82.00 0.5000 0.5000 NA 0.5086 0.6188 0.6189 Average AUC in Table 3 also shows that MFRIS1 archives better performance for most lower IR imbalanced datasets. On the other hand, MFRIS3 records better performance with high IR. MFRIS2 is also a solution for some datasets. In these cases, maybe the number of positive instances is very small so it is impossible to remove some or there is little different among qualities of positive instances. In order to show the statistical significance of the performance of the proposed method, we perform Friedman test [10] to compare the AUC to each of the state-of-the- art algorithms. The Friedman rankings and test statistics are given in Table 4 and Table 5. Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 55 Table 4. Friedman Ranking w.r.t. AUC. Algorithm Ranking w.r.t AUC FRIS 1.8919 FRPSS 3.4595 MFRIS2 3.6892 MFRIS3 4.5541 MFRIS1 4.6486 Table 5. Friedman statistic. N 37 Chi-square 49.7955 df 4 Asymp. Sig. 3.9837e-10 Let’s choose the level of significant as 0.05. Because the significance level (Asymp. Sig.) is less than 0.05, it is plausible that there is an overall significant difference between the mean ranks of these algorithms. Next, we perform the Wilcoxon post hoc test [31] to compare the proposed algorithms with each of the other algorithms. The adjusted p-values with respect to MFRIS1, MFRIS2 and MFRIS3 are given in Table 6, 7 and 8. Table 6. Comparing MFRIS1 with others. MFRIS1 vs p-values FRIS 4.0463e-07 FRPSS 4.3322e-04 MFRIS2 4.2049e-02 MFRIS3 0.3292 Table 7. Comparing MFRIS2 with others. MFRIS2 vs p-values FRIS 1.6983e-04 FRPSS 0.5330 MFRIS1 0.9579 MFRIS3 0.9916 Table 8. Comparing MFRIS3 with others. MFRIS3 vs p-values FRIS 1.4046e-06 FRPSS 5.9737e-03 MFRIS1 0.6708 MFRIS3 8.4063e-03 From these tables, we can see that MFRIS2 performs better than the FRIS algorithm, but is not so significant in comparison with FRPSS. On the other hand, MFRIS1 and MFRIS3 relatively give the same performance, and they both significantly outperform Công nghệ thông tin 56 T. T. Huyen, L. B. Dung, M. Dinh, “Data balancing methods by fuzzy rough sets.” the other algorithms in terms of AUC. To analyze the benefit of the algorithms, average and increasing AUC are depicted in Figure 4. The left plot shows performance of kNN and SVM with and without instance selection methods. The right plot illustrates some increasing to compare with performance without cleansing data. From the figure, it is noticed that the algorithms assist increasing in classification performance in overall. SVM probably receives more support from instance selection methods. Figure 4. Comparing average of AUC (on all datasets) and increase on average of AUC using MFRISs for different classifiers. To compare time consumption among fuzzy rough based instance selection methods, Table 9 shows that the modification of fuzzy rough instance selection with granularity 1.0 = for imbalanced datasets consumes far less than the conventional methods. On the other hands, the proposed algorithms have to spend more time for tuning granularity. In this step, time consuming to calculate approximation of the package is most concern. In comparison among MFRISs, time consumption increases from the first to the third method. Table 9. Prepossessing time (in minutes) for each instance selection method (Datasets with more than 1000 instances). Describe FRIS FRPSS MFRIS1 MFRIS2 MFRIS3 Granularity segment0 4.2682 6.6287 1.9824 2.0654 2.6732 1.00 yeast-0-2-5-6_vs_3-7- 8-9 0.7493 0.7433 0.4502 0.4283 0.5663 1.00 yeast-0-2-5-7-9_vs_3- 6-8 0.7405 0.8229 0.4604 0.4393 0.5682 1.00 ozone_eight_hr 0.1625 0.2711 5.9860 6.1786 7.3651 0.15 shuttle-c0-vs-c4 2.6479 2.7236 1.0280 1.0577 1.3117 1.00 kr-vs-k- one_vs_fifteen 0.2367 0.3219 3.1913 3.1134 3.2165 0.05 yeast4 1.6571 1.6874 0.7349 0.7291 0.9285 1.00 winequality-red-4 1.8274 1.8734 0.9359 0.9348 1.1819 1.00 ozone_one_hr 0.1558 0.1667 5.9767 6.2840 7.4906 0.15 yeast5 1.6490 1.6955 0.7117 0.7337 0.8980 1.00 Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 57 yeast6 1.6440 1.6672 0.7383 0.7215 0.9212 1.00 abalone-19_vs_10-11- 12-13 2.1847 NA 0.9316 0.9337 1.1880 1.00 shuttle-2_vs_5 9.3936 9.4679 2.7952 3.0382 3.6771 1.00 poker-8-9_vs_5 0.4975 NA 1.0288 1.3063 1.4366 1.00 6. CONCLUSION AND FUTURE WORK In this paper, we make an extension of the earlier study with three modification of fuzzy rough instance selection for imbalanced data. By using different criteria in selecting positive and negative classes, it possible to obtain higher classification performance with kNN and SVM. The proposed approach is discussed with mathematical explanation, algorithm presentation and method to optimize parameters. The experiments demo the improvement in performance of the proposed methods. They can also be competitive with state-of-the-art methods while eliminating using other balancing technique such as SMOTE. This paper confirms the robustness of using multiple criteria in fuzzy-rough sets based instance selection approach. It solves problems of automatically choosing parameters that exist in [16]. Further work would be studies on multiple-class imbalanced data selection methods and fuzzy-rough sets based classifier which can deal with imbalanced data. REFERENCES [1]. Jesus Alcala-Fdez, Alberto Fernandez, Julian Luengo, Joaquin Derrac, and Salvador Garcia. Keel data-mining software tool: “Data set repository, integration of algorithms and experimental analysis framework.” Multiple-Valued Logic and Soft Computing, 17(2- 3):255–287, 2011. [2]. K. Bache and M. Lichman. “UCI Machine Learning Repository”, 2013. [3]. Yaile Caballero, Rafael Bello, Delia Alvarez, Maria M. Gareia, and Yaimara Pizano. “Improving the k-nn method: Rough set in edit training set”. In John Debenham, editor, Professional Practice in Artificial Intelligence, volume 218 of IFIP International Federation for Information Processing, pages 21–30. Springer US, 2006. [4]. Nitesh V. Chawla, Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. “Smote: Synthetic minority over-sampling technique”. Journal of Artificial Intelligence Research, 16:321–357, 2002. [5]. Chris Cornelis, Nele Verbiest, and Richard Jensen. “Ordered weighted average based fuzzy rough sets”. In Rough Set and Knowledge Technology - 5th International Conference, RSKT 2010, Beijing, China, October 15- 17, 2010. Proceedings, pages 78–85, 2010. [6]. Corinna Cortes and Vladimir Vapnik. “Support-vector networks”. Machine Learning, 20(3):273–297, 1995. [7]. T. Cover and P. Hart. “Nearest neighbor pattern classification”. IEEE Trans. Inf. Theor., 13(1):21–27, September 1967. [8]. Didier Dubois and Henri Prade. “Rough fuzzy sets and fuzzy rough sets”. In International Journal of General Systems, volume 17, pages 191–209. 1990. [9]. Didier Dubois and Henri Prade. “Putting rough sets and fuzzy sets together. In Roman Slowinski”, editor, Intelligent Decision Support, volume 11 of Theory and Decision Library, pages 203–232. Springer Netherlands, 1992. [10]. Friedman, M. “The use of ranks to avoid the assumption of normality implicit in the analysis Công nghệ thông tin 58 T. T. Huyen, L. B. Dung, M. Dinh, “Data balancing methods by fuzzy rough sets.” of variance”. Journal of the American Statistical Association, 32(200):675–701, 1973. [11]. Grzymala-Busse, J. W., Clark, P. G., and Kuehnhausen, M. “Generalized probabilistic approximations of incomplete data”. International Journal of Approximate Reasoning, 55(1, Part 2):180 – 196. Special issue on Decision-Theoretic Rough Sets, 2014. [12]. Jin Huang and C.X. Ling. “Using auc and accuracy in evaluating learning algorithms”. Knowledge and Data Engineering, IEEE Transactions on, 17(3):299 310, March 2005. [13]. R. Jensen and C. Cornelis. “Fuzzy-rough instance selection”. In Fuzzy Systems (FUZZ), 2010 IEEE International Conference on, pages 1–7, July 2010. [14]. Marzena Kryszkiewicz. “Rough set approach to incomplete information systems”. Inf. Sci., 112(1-4):39–49, December 1998. [15]. Victoria Lopez, Alberto Fernandez, Salvador Garcia, Vasile Palade, and Francisco Herrera. “An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics”. Information Sciences, 250(0):113 – 141, 2013. [16]. Do Van Nguyen, Keisuke Ogawa, Kazunori Matsumoto, and Masayuki Hashimoto. “Editing training sets from imbalanced data using fuzzyrough sets”. In IFIP Advances in Information and Communication Technology, volume 458, pages 115–129, France, 2015. [17]. Do Van Nguyen, Koichi Yamada, and Muneyuki Unehara. “Extended tolerance relation to define a new rough set model in incomplete information systems”. Advances in Fuzzy Systems, 2013. Article ID 372091. [18]. Do Van Nguyen, Koichi Yamada, and Muneyuki Unehara. “On probability of matching in probability based rough set definitions”. In IEEESMC2013, pages 449–454, Manchester, The UK, 2013. [19]. Nguyen, D. V., Yamada, K., and Unehara, M. “Rough set approach with imperfect data based on dempster-shafer theory”. Journal of Advanced Computational Intelligence and Intelligent Informatics, 18(3):280–288, 2014. [20]. Nguyen, H. S. “Discretization problem for rough sets methods”. In Proceedings of the First International Conference on Rough Sets and Current Trends in Computing, RSCTC ’98, pages 545–552, London, UK, UK. Springer-Verlag, 1998. [21]. Zdzislaw Pawlak. “Rough sets”. International Journal of Computer and Information Sciences, 11:341–356, 1982. [22]. Zdzislaw Pawlak. “Rough Sets”. Theoretical Aspects of Reasoning about Data. Kluwer Acad., 1991. [23]. Anna Maria Radzikowska and Etienne E. Kerre. “A comparative study of fuzzy rough sets”. Fuzzy Sets Syst., 126(2):137–155, March 2002. [24]. Enislay Ramentol, Yaile Caballero, Rafael Bello, and Francisco Herrera. SMOTE-RSB *: “A hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-sets using SMOTE and rough sets theory”. Knowl. Inf. Syst., 33(2):245– 265, 2011. [25]. Enislay Ramentol, Nele Verbiest, Rafael Bello, Yaille Caballero, Chris Cornelis, and Francisco Herrera. Smote-frst: “A new resampling method using fuzzy rough set theory”. In Cengiz Kahraman, Etienne Kerre, and Faik Tunc Bozbura, editors, World Scientific Proceedings Series on Computer Engineering and Decision Making, volume 7, pages 800– 805. World Scientific, 2012. [26]. Enislay Ramentol, Sarah Vluymans, Nele Verbiest, Yaille Caballero, Rafael Bello, Chris Cornelis, and Francisco Herrera. Ifrowann: “Imbalanced fuzzy rough ordered weighted average nearest neighbor classification”. In IEEE Transaction on Fuzzy System, volume 23, 2012. [27]. Verbiest, N. Multi threshold frps: “A new approach to fuzzy rough set prototype selection”. In RSCTC 2014, LNAI, volume 8536, pages 83–91, 2014. [28]. Nele Verbiest, Chris Cornelis, and Francisco Herrera. Frps: “A fuzzy rough prototype Nghiên cứu khoa học công nghệ Tạp chí Nghiên cứu KH&CN quân sự, Số Đặc san CNTT, 12 - 2020 59 selection method”. Pattern Recognition, 46(10):2770 – 2782, 2013. [29]. Nele Verbiest, Enislay Ramentol, Chris Cornelis, and Francisco Herrera. “Preprocessing noisy imbalanced datasets using SMOTE enhanced with fuzzy rough prototype selection”. Appl. Soft Comput., 22:511–517, 2014. [30]. Sarah Vluymans, Danel Sanchez Tarrago, Yvan Saeys, Chris Cornelis, and Francisco Herrera. “Fuzzy rough classifier for class imbalanced multi-instance data”. Pattern Recognition, 53:36–45, 2016. [31]. Wilcoxon, F. “Individual comparisons by ranking methods”. Biometrics Bulletin, 1(6):80– 83, 1945. [32]. Ronald R. Yager. “On ordered weighted averaging aggregation operators in multicriteria decisionmaking”. IEEE Trans. Syst. Man Cybern., 18(1):183–190, January 1988. [33]. Y. Y. Yao. “Combination of rough and fuzzy sets based on -level sets”. In Rough sets and data mining: Analysis for imprecise data, pages 301– 321. Kluwer Academic, 1997. [34]. Hans-Jurgen Zimmermann. “Fuzzy Set Theory and its Applications”. Springer, 2001. TÓM TẮT PHƯƠNG PHÁP CÂN BẰNG DỮ LIỆU BẰNG TẬP HỢP THÔ MỜ Sự hiệu quả của lý thuyết tập hợp thô trong việc làm sạch dữ liệu đã được chứng minh trong nhiều nghiên cứu. Gần đây, tập thô mờ cũng thực hiện xử lý dữ liệu mất cân bằng bằng hai cách tiếp cận. Đầu tiên là sự kết hợp của các phương pháp cân bằng và trích chọn đối tượng thô mờ. Phương pháp thứ hai cố gắng sử dụng các tiêu chí khác nhau để làm sạch các lớp đa số và thiểu số trong dữ liệu mất cân bằng. Công việc này là một phần mở rộng của phương pháp thứ hai đã được trình bày trong [15]. Bài báo mô tả nghiên cứu đầy đủ về phương pháp thứ hai với một số thuật toán được đề xuất. Nó tập trung chủ yếu vào phân loại nhị phân với kNN và SVM cho dữ liệu không cân bằng. Các thử nghiệm và so sánh giữa các phương pháp có liên quan sẽ xác nhận ưu điểm và xu hướng của từng phương pháp về độ chính xác của hiệu suất và mức tiêu thụ thời gian. Từ khóa: Lý thuyết tập hợp thô; Tập thô mờ; Tính toán hạt; Trích chọn đối tượng. Received 21st October 2020 Revised 10th December 2020 Accepted 15th December 2020 Author affiliations: 1UET, Vietnam National University, Hanoi, Vietnam; 2Institute of Information Technology, Hanoi, Vietnam; 3IOIT, Vietnam Academy of Science and Technology; 4Military College of Tank-Armour Officers. *Corresponding author: huyenmit82@gmail.com.
File đính kèm:
 data_balancing_methods_by_fuzzy_rough_sets.pdf
data_balancing_methods_by_fuzzy_rough_sets.pdf

