Cơ sở Toán học và yếu tố thực tiễn của một số kiến thức toán tiểu học

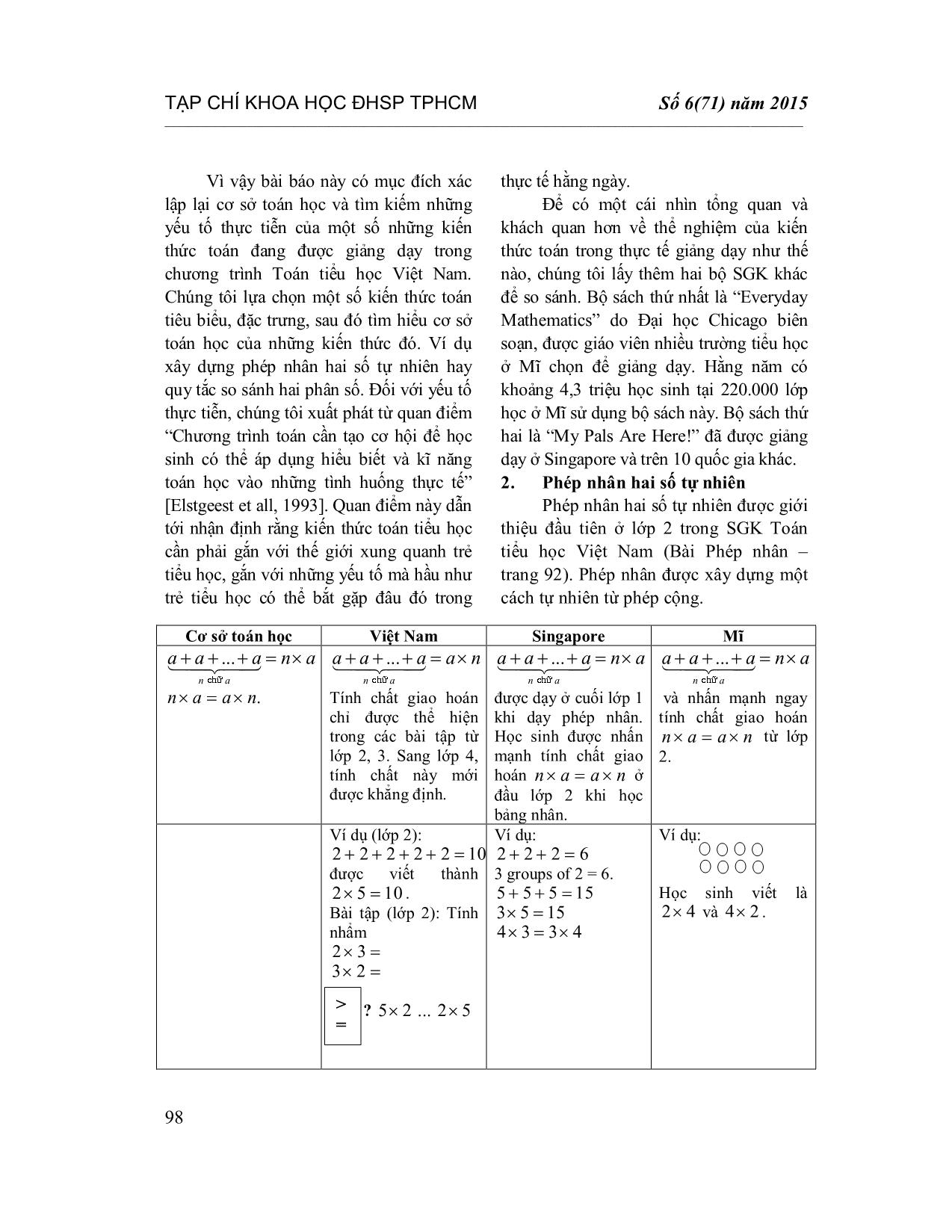
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Minh Thành 
_____________________________________________________________________________________________________________ 
97 
CƠ SỞ TOÁN HỌC VÀ YẾU TỐ THỰC TIỄN 
CỦA MỘT SỐ KIẾN THỨC TOÁN TIỂU HỌC 
DƯƠNG MINH THÀNH* 
TÓM TẮT 
Bài báo này điểm lại cơ sở toán học và yếu tố thực tiễn hình thành nên một số kiến 
thức toán tiểu học. Để có cái nhìn khách quan, chúng tôi xem xét các kiến thức toán đó 
trong những bộ sách giáo khoa (SGK) khác nhau hiện đang được giảng dạy tại Việt Nam, 
Singapore và Mĩ. 
Từ khóa: kiến thức toán, sách giáo khoa, yếu tố thực tiễn, thiết kế chương trình. 
ABSTRACT 
The mathematic foundation and practical factors of some math knowledge 
at primary schools 
This article reviews the mathematic foundation and practical factors that form some 
math knowledge for primary education. In order to have an objective view, the researcher 
examines such knowledge in various textbooks that are currently used in Vietnam, 
Singapore and the US. 
Keywords: Math knowledge, textbook, practical factor, curriculum design. 
* TS, Trường Đại học Sư phạm TPHCM; Email: thanhdmi@hcmup.edu.vn 
1. Giới thiệu 
Đào tạo giáo viên tiểu học là một 
công việc phức tạp ở đó đơn vị đào tạo 
phải có trách nhiệm giúp sinh viên chuẩn 
bị kĩ lưỡng kiến thức về phương pháp 
dạy học cũng như phải giúp họ nắm được 
kiến thức toán tiểu học (và nhiều kiến 
thức khác) ở mức độ am hiểu. Ví dụ một 
giáo sinh tiểu học khi ra trường cần phải 
trả lời thành thục những câu hỏi “Phân số 
là gì?”, “Làm sao giúp học sinh so sánh 
được hai phân số?”, “Cộng hai phân số 
được giải thích như thế nào?”. Do đó dẫn 
tới việc cần phải xác lập cơ sở toán học 
của các kiến thức toán tiểu học. Điều này 
không chỉ giúp cơ sở đào tạo giáo viên 
tiểu học xây dựng chương trình toán bậc 
đại học mà còn giúp các nhà soạn thảo 
chương trình, SGK có thêm thông tin về 
yếu tố khoa học toán học (bên cạnh khoa 
học giáo dục) để đưa ra được cách tối ưu 
trong việc truyền tải kiến thức đó đến 
được đối tượng học sinh. 
Một khía cạnh khác ảnh hưởng đến 
việc lựa chọn một kiến thức cũng như 
mức độ của nó để đưa vào trong SGK là 
yếu tố thực tiễn. Ở bậc tiểu học, với đặc 
trưng hình thành kiến thức toán ở mức độ 
nhận diện hoặc phát hiện, hình thành 
những quy tắc cơ bản đầu tiên của toán 
học (chẳng hạn quy tắc đếm) thì đòi hỏi 
phải chú ý đến yếu tố thực tiễn. Đối với 
học sinh tiểu học, khó có thể xuất phát từ 
một tình huống toán học để xây dựng một 
kiến thức toán học tiếp theo mà phải xuất 
phát từ một yếu tố thực tế, thực tế ở đây 
gắn với thế giới xung quanh học sinh. 
Cách xuất phát này cũng giúp dẫn đến cái 
đích cuối cùng: học sinh thấy được yếu tố 
toán học trong đời sống thực tiễn. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 6(71) năm 2015 
_____________________________________________________________________________________________________________ 
98 
Vì vậy bài báo này có mục đích xác 
lập lại cơ sở toán học và tìm kiếm những 
yếu tố thực tiễn của một số những kiến 
thức toán đang được giảng dạy trong 
chương trình Toán tiểu học Việt Nam. 
Chúng tôi lựa chọn một số kiến thức toán 
tiêu biểu, đặc trưng, sau đó tìm hiểu cơ sở 
toán học của những kiến thức đó. Ví dụ 
xây dựng phép nhân hai số tự nhiên hay 
quy tắc so sánh hai phân số. Đối với yếu tố 
thực tiễn, chúng tôi xuất phát từ quan điểm 
“Chương trình toán cần tạo cơ hội để học 
sinh có thể áp dụng hiểu biết và kĩ năng 
toán học vào những tình huống thực tế” 
[Elstgeest et all, 1993]. Quan điểm này dẫn 
tới nhận định rằng kiến thức toán tiểu học 
cần phải gắn với thế giới xung quanh trẻ 
tiểu học, gắn với những yếu tố mà hầu như 
trẻ tiểu học có thể bắt gặp đâu đó trong 
thực tế hằng ngày. 
Để có một cái nhìn tổng quan và 
khách quan hơn về thể nghiệm của kiến 
thức toán trong thực tế giảng dạy như thế 
nào, chúng tôi lấy thêm hai bộ SGK khác 
để so sánh. Bộ sách thứ nhất là “Everyday 
Mathematics” do Đại học Chicago biên 
soạn, được giáo viên nhiều trường tiểu học 
ở Mĩ chọn để giảng dạy. Hằng năm có 
khoảng 4,3 triệu học sinh tại 220.000 lớp 
học ở Mĩ sử dụng bộ sách này. Bộ sách thứ 
hai là “My Pals Are Here!” đã được giảng 
dạy ở Singapore và trên 10 quốc gia khác. 
2. Phép nhân hai số tự nhiên 
Phép nhân hai số tự nhiên được giới 
thiệu đầu tiên ở lớp 2 trong SGK Toán 
tiểu học Việt Nam (Bài Phép nhân – 
trang 92). Phép nhân được xây dựng một 
cách tự nhiên từ phép cộng. 
Cơ sở toán học Việt Nam Singapore Mĩ 
...
n a
a a a n a 
chöõ
.n a a n 
...
n a
a a a a n 
chöõ
Tính chất giao hoán 
chỉ được thể hiện 
trong các bài tập từ 
lớp 2, 3. Sang lớp 4, 
tính chất này mới 
được khẳng định. 
...
n a
a a a n a 
chöõ
được dạy ở cuối lớp 1 
khi dạy phép nhân. 
Học sinh được nhấn 
mạnh tính chất giao 
hoán n a a n ở 
đầu lớp 2 khi học 
bảng nhân. 
...
n a
a a a n a 
chöõ
 và nhấn mạnh ngay 
tính chất giao hoán 
n a a n t ... pore 
cũng được học tương tự như vậy: “Three 
times of five equals fifteen, three times of 
six equals eighteen...”. 
3. Bài toán tìm x 
Bài toán tìm x xuất hiện đầu tiên ở 
lớp 2 trong chương trình Toán tiểu học 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 6(71) năm 2015 
_____________________________________________________________________________________________________________ 
100 
của Việt Nam (Bài Phép trừ có nhớ trong 
phạm vi 100 – trang 45). Nhiều giáo viên 
được hỏi công nhận rằng, đối với học sinh 
có học lực trung bình hoặc yếu, các em hay 
bị nhầm lẫn trong bài toán tìm x , nhất là 
đối với bài toán trừ và bài toán chia. 
Cơ sở 
toán học Việt Nam Singapore Mĩ 
Nếu a b thì 
a c b c , 
a c b c , 
: :a d b d 
với 0d . 
Muốn tìm một số hạng ta lấy 
tổng trừ đi số hạng kia. 
Muốn tìm số bị trừ ta lấy hiệu 
cộng với sô trừ. 
Muốn tìm số trừ ta lấy số bị 
trừ trừ đi hiệu. 
Muốn tìm một thừa số ta lấy 
tích chia cho thừa số kia. 
Muốn tìm số bị chia ta lấy 
thương nhân với số chia (lớp 
2). 
Trong phép chia hết, muốn 
tìm số chia ta lấy số bị chia 
chia cho thương3 (lớp 3). 
Ví dụ (lớp 2): 
3 9
 9 3
 6
x
x
x
Ở lớp 6 (lớp 
cuối cấp tiểu 
học), học sinh 
được học biểu 
thức đại số và 
rút gọn biểu 
thức đại số, ví 
dụ: 
Tìm giá trị biểu 
thức 
2
3
y 
 khi 
8y . 
Rút gọn 
4a a . 
Sau đó học sinh 
học giải toán có 
lời văn có thiết 
lập biểu thức 
đại số. 
Cho ví dụ 
48 + d = 70 
Đáp án 
48 + 22 =70 
Sau đó cho các bài tập 
34 7x 
5 35m 
5 /10w 
Lưu ý: bài toán này 
xuất hiện đầu tiên ở 
lớp 4, nhấn mạnh sự 
phán đoán kết quả chứ 
không sử dụng quy 
tắc. Lên cấp 2, học 
sinh mới được học 
quy tắc. 
Bài toán tìm x thực chất là một 
kiểu bài toán giải phương trình. Theo 
[Bennett et all, 2012], một chữ cái hoặc 
một kí hiệu được dùng để thay thế cho 
một số chưa biết được gọi là biến số. 
Biến số cùng với các phép toán cộng, trừ, 
nhân và chia cho ta một biểu thức đại số. 
Hai biểu thức đại số bằng nhau cho ta 
khái niệm phương trình. 
Như vậy trong SGK Toán tiểu học 
của Việt Nam, bài toán chứa biến số đã 
xuất hiện từ lớp 1 ở dạng bài toán “Điền 
số thích hợp vào chỗ trống”, chỗ trống ở 
đây có thể là dấu 3 chấm, ô trống Đối 
với dạng toán này học sinh sẽ đoán nhận 
số để điền vào sao cho thu được một 
phép tính đúng4. Điều này phù hợp với 
quan điểm dạy học trong SGK Toán tiểu 
học của Mĩ và Singapore: việc tìm x chỉ 
cần ở mức độ đoán nhận kết quả. Lưu ý 
rằng, trong SGK Toán tiểu học của Mĩ, 
chữ cái x (kí hiệu đại số) được thay thế 
bằng nhiều chữ cái khác nhau. 
Ở Mĩ và nhiều nước khác, đối với bài 
toán tìm x việc sử dụng các quy tắc hay 
thuật giải được dạy ở cấp 2. Học sinh được 
khuyến khích sử dụng các quy tắc biến đổi 
trên đẳng thức như ở cột thứ nhất (quy tắc 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Minh Thành 
_____________________________________________________________________________________________________________ 
101 
biến đổi trên bất đẳng thức để giải bất 
phương trình cũng tương tự). Thậm chí học 
sinh có thể tự đưa ra một quy tắc nào đó. 
Ví dụ để tìm x từ bài toán 3 4 19x , 
học sinh có thể làm như sau: 
Xuất phát từ x học sinh vẽ các mũi 
tên 
3 4
:3 4
3 19
5 15 19
x x 
  
 
và kết luận 5x . Có thể hình dung quan 
điểm dạy học toán của họ ở đây là học 
sinh tính đúng kết quả và giải thích được 
nó một cách hợp lí. 
Ngoài ra giáo viên sẽ đưa thêm mô 
hình thực tế để học sinh hiểu về các quy 
tắc này, chẳng hạn mô hình ở Hình 2 (chi 
tiết hơn, đọc giả có thể xem trong tài liệu 
[Bennett et all, 2012]). 
Hình 2. Cơ sở toán học và yếu tố thực tiễn của bài toán tìm x 
4. So sánh phân số 
Cơ sở toán học Việt Nam Singapore Mĩ 
a c
b d
 khi và 
chỉ khi 
ad bc . 
a c
b d
 khi và 
chỉ khi 
ad bc . 
Chú ý ở đây 
- Nếu nhân (hoặc chia) cả tử 
số mà mẫu số với cùng một 
số tự nhiên khác 0 thì được 
một phân số bằng phân số 
đã cho5. 
Ví dụ: 
10 10 : 5 2
15 15 : 5 3
Ở lớp 2, học sinh 
được học cách sử 
dụng fraction 
strip (tạm dịch là 
dải phân số) để so 
sánh phân số. Lên 
lớp 3, sau khi học 
các phân số bằng 
nhau, học sinh 
học cách so sánh 
Phân số được dạy 
đầu tiên ở lớp 1 với 
các phân số đơn giản 
dạng một phần n 
với 10n . Học 
sinh sử dụng fraction 
strip để so sánh. 
Đến lớp 3, học sinh 
vẫn sử dụng fraction 
strip (nhưng không 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 6(71) năm 2015 
_____________________________________________________________________________________________________________ 
102 
đang xét kiến 
thức toán tiểu 
học nên không 
cần thiết đề cập 
điều kiện số 
dương. 
Vậy 
10 2
15 3
Muốn so sánh hai phân số 
khác mẫu số, ta có thể quy 
đồng mẫu số hai phân số đó, 
rồi so sánh các tử số của hai 
phân số mới (lớp 4). 
Ví dụ: 
2 2 4 8
3 3 4 12
; 
3 3 3 9
4 4 3 12
. 
Vì 
8 9
12 12
 nên 
2 3
3 4
 . 
hai phân số bằng 
cách đưa về cũng 
mẫu số. 
được tô màu) để so 
sánh phân số (và hỗn 
số) sau đó được học 
cách so sánh phân số 
bằng cách đưa về 
cùng mẫu số. 
Ở khía cạnh toán học thuần túy, 
phân số (đang xét là không âm) được 
định nghĩa từ số tự nhiên. Điều này dẫn 
đến khi xem xét mối quan hệ giữa các 
phân số (kiến thức khó hơn – kiến thức 
được xây dựng), người ta chuyển về xét 
mối quan hệ trên các số tự nhiên (kiến 
thức dễ hơn – kiến thức dùng để xây 
dựng). Do đó lí do tại sao có cơ sở toán 
học trong cột thứ nhất ở trên là hoàn toàn 
dễ hiểu. 
Đối với kiến thức trong cột thứ hai, 
để giải quyết một vấn đề trên phân số, 
người ta chuyển về một vấn đề khác cũng 
trên phân số. Điều đó đưa đến nhiều khó 
khăn cho học sinh hơn6. Tuy nhiên, nếu 
chuyển bài toán so sánh trên phân số về 
bài toán so sánh trên số tự nhiên có thể 
dẫn đến việc mất đi bản chất của khái 
niệm phân số. Do đó ở Singapore hoặc Mĩ 
người ta vẫn sử dụng phương pháp giống 
ở Việt Nam nhưng trước đó việc để so 
sánh các phân số học sinh được dùng một 
công cụ hiệu quả là các “fraction strip”. 
Hình 3. Mô hình fraction strip 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Minh Thành 
_____________________________________________________________________________________________________________ 
103 
5. Các hình hình học 
Cơ sở toán học Việt Nam Singapore Mĩ 
Đa giác là một 
đường gấp khúc 
phẳng khép kín. 
Hình đa diện gồm 
một số hữu hạn các 
đa giác phẳng thỏa 
mãn hai điều kiện: 
- Hai đa giác bất 
kì hoặc không có 
điểm chung, hoặc có 
một đỉnh chung, 
hoặc có một cạnh 
chung. 
- Mỗi cạnh của 
một đa giác là cạnh 
chung của đúng hai 
đa giác. 
Tam giác, tứ giác, 
hình thang, hình 
bình hành, hình chữ 
nhật, hình thoi, hình 
vuông. 
Hình hộp chữ nhật, 
hình lập phương, 
hình trụ, hình cầu. 
Hình vẽ tứ giác chỉ 
trong trường hợp tứ 
giác lồi. 
Bài tập có các dạng: 
nhận diện, đếm số 
hình, tính toán. 
Học sinh chủ yếu 
được dạy tính toán 
trên các hình hình 
học. 
Đa giác đơn giản và 
hình tròn đã được 
gọi tên ở lớp 1, sang 
lớp 2 thì học sinh 
được học cả đa giác 
không lồi, nhiều 
cạnh cũng như các 
hình 3 chiều: hình 
trụ, hình cầu, hình 
nón, hình hộp chữ 
nhật, hình lập 
phương. 
Học sinh được học 
về sự đối xứng ở lớp 
4. 
Bài tập tính toán 
nhiều trên các hình 
khá phức tạp và 
nhiều ví dụ gắn với 
thực tế. 
Đa giác nhiều cạnh 
đã xuất hiện ở lớp 1 
(chưa được đặt tên) 
và chính thức được 
dạy ở lớp 2 (không 
phân biệt tính chất 
lồi hoặc không lồi) 
cùng với hình trụ, 
hình cầu, hình nón, 
hình chóp (vẽ ở các 
góc độ khác nhau). 
Bài tập đa dạng: 
nhận diện, phát hiện 
hình hình học từ đồ 
vật hoặc hình ảnh 
thực tế, phát hiện 
tính đối xứng của 
hình, tính toán 
Học sinh được dạy 
về thế giới hình học 
và ứng dụng của 
chúng. 
Một bài tập đã được tác giả đưa ra dành cho giáo viên tiểu học như sau: 
Hãy đếm số tứ giác ở hình trên. 
Trong số gần 100 giáo viên tiểu học được hỏi, chỉ vài giáo viên trả lời đúng là 6 
tứ giác. Điều đó cho thấy phần lớn giáo viên bị hiểu nhầm khái niệm “tứ giác” đồng 
nhất với khái niệm “tứ giác lồi”. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 6(71) năm 2015 
_____________________________________________________________________________________________________________ 
104 
6. Chu vi hình tròn 
Cơ sở 
toán học Việt Nam Singapore Mĩ 
Trong một 
hình tròn, tỉ 
số giữa chu 
vi và đường 
kính bằng pi 
( ), con số 
này xấp xỉ 
3,14. 
Ở lớp 5, học sinh 
được hướng dẫn 
đo chu vi hình 
tròn bằng cách 
lăn hình tròn trên 
thước thẳng, sau 
đó đưa ra cách 
tính: 
Muốn tính chu vi 
của hình tròn ta 
lấy đường kính 
nhân với 3,14 7. 
Ở cuối lớp 6, học 
sinh được học về 
hình tròn, bán 
kính, đường kính 
và chu vi (qua ví 
dụ độ dài bao 
quanh bánh xe 
đạp). Sau đó người 
ta cho một bảng 
thống kê kết quả 
đo chu vi và 
đường kính của 
một số hình tròn 
rồi yêu cầu tính tỉ 
số để tìm ra số . 
Ở lớp 5, học sinh được hướng dẫn 
dùng thước đo cẩn thận chu vi 
hình tròn C và đường kính d 
chính xác tới milimet (đo tách trà, 
dĩa đựng đồ ăn,). Sau đó lập 
bảng ghi nhận các tỉ số 
C
d
 rồi 
tính giá trị trung bình của chúng. 
Sau bài đo diện tích hình tròn 
(bằng ước lượng), số pi mới được 
giới thiệu là tỉ số của chu vi và 
đường kính hoặc tỉ số giữa diện 
tích và bình phương bán kính. 
7. Kết luận 
Một kiến thức toán học được đưa 
vào giảng dạy cho học sinh tiểu học 
ngoài việc được lựa chọn một cách cẩn 
thận còn phải gắn liền với việc xây dựng 
cách thức tiến hành dạy học một cách 
hợp lí. Không những thế, kiến thức đó 
phải là sự kết hợp hài hòa giữa cơ sở 
toán học và yếu tố thực tiễn gắn liền với 
thế giới của trẻ. Ví dụ từ bài so sánh 
phân số cho ta thấy rằng, nếu chỉ nhấn 
mạnh yếu tố toán học (cho dù nhằm 
giúp học sinh tính toán dễ dàng hơn) thì 
có thể dẫn đến việc làm mất đi ý nghĩa 
thực tiễn của kiến thức. Do đó đối với 
các nhà giáo dục, những người biên 
soạn chương trình, viết SGK, ngoài việc 
họ cần phải am hiểu các khái niệm toán 
học ở tiểu học còn phải biết gắn mình 
vào vị trí của học sinh tiểu học để có thể 
biết được mình phải viết kiến thức đó 
như thế nào. 
Ngoài ra, một điểm cần phải chú ý 
rằng kiến thức trong SGK phải liên tục 
được cập nhật. Chẳng hạn ngày nay 
“tiền” là một khái niệm quen thuộc với 
trẻ nhỏ và chúng đã có cơ hội tiếp xúc 
với tiền từ rất sớm. Vì vậy không thể né 
tránh việc dạy “tiền” ở tiểu học. Tuy 
nhiên trong chương trình Toán hiện nay ở 
Việt Nam, những bài liên quan đến tiền 
được xếp vào những nội dung giảm tải. 
Chưa kể, kiến thức về nó không được cập 
nhật thường xuyên, ví dụ tiền cotton 
mệnh giá 10 nghìn và 20 nghìn đồng đã 
được Ngân hàng Nhà nước Việt Nam 
chính thức thu hồi từ ngày 01-01-2013 
nhưng trong SGK Toán lớp 3, hình ảnh 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Minh Thành 
_____________________________________________________________________________________________________________ 
105 
của những tờ tiền đó vẫn đang được sử 
dụng. 
Một ví dụ khác cho việc SGK Toán 
tiểu học của Việt Nam thiếu yếu tố thực 
tiễn mà chỉ chú ý đến tính đầy đủ của 
kiến thức là các bài dạy về đơn vị đo 
lường. Trong thực tế người ta không sử 
dụng các đơn vị đo: héc-tô-mét8, đề-ca-
mét, héc-tô-gam, đề-ca-gam, héc-tô-mét 
vuông, đề-ca-mét vuông nhưng nó vẫn 
được giảng dạy ở tiểu học (thậm chí đơn 
vị đề-xi-mét tưởng chừng là quen thuộc 
nhưng người ta không sử dụng trong thực 
tế)9. Trong khi những đơn vị đo lường 
thông dụng hoặc những thuật ngữ địa 
phương (cân, kí, tấc, lạng) thì không xuất 
hiện trong SGK một cách chính thức 
giống như tấn, tạ, yến. _ 
1 G. Polya (How to solve): “Một trong những nhiệm vụ quan trọng nhất của giáo viên là giúp đỡ học sinh. Để 
làm được điều đó, giáo viên cần đặt mình vào vị trí của học sinh”. Do đó trong trường hợp dạy phép nhân, 
học sinh nên được biết tính chất giao hoán để giảm khối lượng phép tính cần phải nhớ. 
2 Có giáo viên đề nghị một phương án rằng, để giúp học sinh phát hiện ra 2 0 0 giáo viên có thể nhắc lại 
các phép tính 2 3 6 , 2 2 4 , 2 1 2 rồi hỏi 2 0 bằng bao nhiêu. Có giáo viên khác đề xuất một 
cách giải thích một cách thực tế hơn cho phép tính 2 0 0 : “có 2 cái kẹo nhưng không tính lần nào”. Tuy 
nhiên có người cho rằng, thay vì tìm cách giải thích để học sinh hiểu vai trò của số 0 trong phép tính, chúng 
ta có thể đưa ra kết quả 2 0 0 như là một quy ước (được hiểu là một quy tắc bắt buộc). 
3 Nhiều giáo viên phản ánh rằng, học sinh trung bình yếu thường nhầm lẫn giữa số bị trừ và số trừ, tương tự 
các em cũng hay nhầm lẫn giữa số bị chia và số chia. 
4 Một số giáo viên công nhận rằng, đối với dạng toán “Điền số thích hợp vào chỗ trống” giải bằng cách đoán 
nhận số, học sinh ít làm sai hơn bài toán tìm x giải bằng quy tắc. 
5 Điều này có nghĩa là hai phân số bằng nhau nếu phân số này sau một phép biến đổi (nhân hoặc chia cả tử số 
và mẫu số cho cùng một số) sẽ thành phân số kia. 
6 Nhiều giáo viên được hỏi công nhận rằng, nếu dạy theo cách được đưa ra trong cột thứ nhất, học sinh dễ 
làm bài và khó sai hơn. 
7 Nếu dạy về hình tròn như thế thì học sinh sẽ không hiểu được ý nghĩa của số pi. Đồng thời bài tập chỉ dừng 
lại ở việc tính hoặc là chu vi hoặc là bán kính. 
8 Có người cho rằng dạy héc-tô-mét để học sinh có thể hiểu được khái niệm héc-ta. Tuy nhiên ta hoàn toàn có 
thể dùng đơn vị mét để định nghĩa hecta mà không cần phải thông qua đơn vị héc-tô-mét. Theo định nghĩa 
quốc tế, một héc-ta (hectare) chỉ đơn giản là bằng 10 000 m2. 
9 Ở Singapore người ta chỉ dạy những đơn vị mà học sinh có thể cảm nhận được ngoài thực tế: ki-lô-mét, 
mét, xăng-ti-mét, ki-lô-gam, gam, lít, mi-li-lít, mét vuông, xăng-ti-mét vuông 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 6(71) năm 2015 
_____________________________________________________________________________________________________________ 
106 
TÀI LIỆU THAM KHẢO 
1. Đỗ Đình Hoan (chủ biên) (2013), Toán 1, 2, 3, 4, 5, Tái bản lần thứ 9 và 10, Nxb 
Giáo dục Việt Nam. 
2. A. B. Bennett, L. J. Burton and L. T. Nelson (2012), Mathematics for Elementary 
Teachers: A Conceptual Approach, Ninth Edition, Mc Graw Hill. 
3. G. Polya (1957), How to solve it, Second Editon, Princeton University Press, 
Princeton, New Jersey. 
4. The University of Chicago School Mathematics Project (2007), Everyday 
Mathematics, Student Math Journal, Grades 1 – 5, Mc Graw Hill. 
5. Fong Ho Kheong, Chelvi Ramakrishman and Bernice Lau Pui Wah (2013), My Pals 
Are Here!, Grades 1 – 6, Marshall Cavendish Education. 
6. Trần Diên Hiển, Bùi Huy Hiển (2007), Các tập hợp số, Dự án phát triển giáo viên 
tiểu học, Nxb Giáo dục. 
7. J. Elstgeest, F. Goffree and W. Harlen (1993), “Education for Teaching Science and 
Mathematics in the Primary School”, Published by United Nations Educational, 
Scientific and Cultural Organization, Printed by UNESCO. 
(Ngày Tòa soạn nhận được bài: 19-4-2015; ngày phản biện đánh giá: 11-5-2015; 
ngày chấp nhận đăng: 05-6-2015)