Bài giảng Tín hiệu và hệ thống - Chương 2, Phần 1: Phân tích hệ thống trong miền thời gian - Đinh Thị Mai
Hệ thống liên tục
• Phương trình vi phân của hệ thống LTI liên tục
• Biểu diễn hệ thống bằng đáp ứng xung
• Mô hình biến trạng tháiPhương trình vi phân của hệ thống LTI
• Phương trình vi phân là loại mô hình toán học được
sử dụng phổ biến nhất để biểu diễn các hệ thống trong
nhiều lĩnh vực khác nhau
• Đối với các hệ thống vật lý, phương trình vi phân
biểu diễn hệ thống được thiết lập từ các phương trình
của các định luật vật lý mà hoạt động của hệ thống
tuân theo
• Các hệ thống LTI được biểu diễn bởi các phương
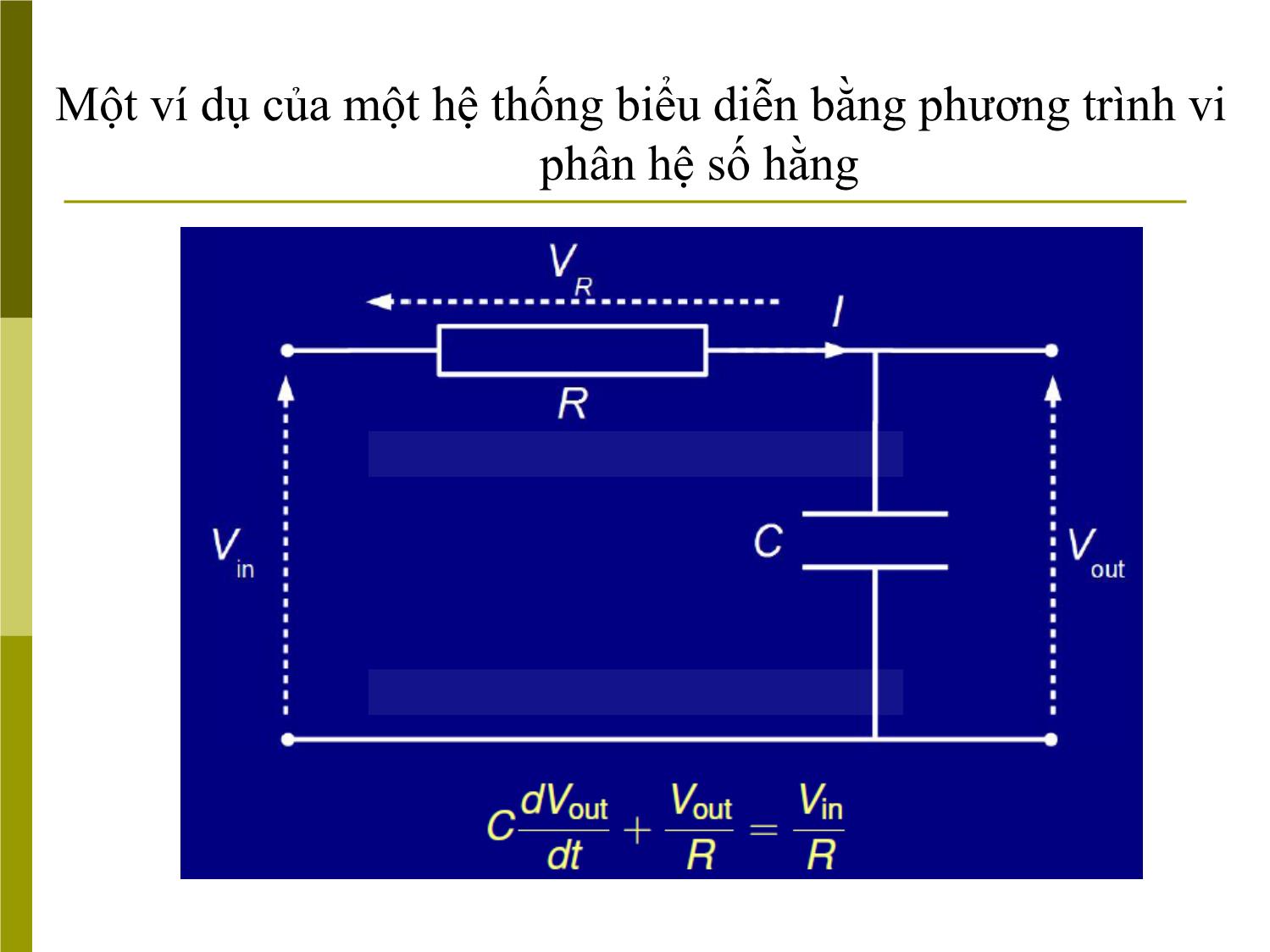
trình vi phân tuyến tính hệ số hằngMột ví dụ của một hệ thống biểu diễn bằng phương trình vi
phân hệ số hằngPhương trình vi phân của hệ thống LTI
• Dạng tổng quát của các phương trình vi phân tuyến
tính hệ số hằng biểu diễn các hệ thống tuyến tính bất
biến:
với x(t) là tín hiệu lối vào, y(t) là tín hiệu lối ra của hệ thống
• Giải phương trình vi phân tuyến tính nói trên cho
phép xác định tín hiệu ra y(t) theo tín hiệu vào x

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Tín hiệu và hệ thống - Chương 2, Phần 1: Phân tích hệ thống trong miền thời gian - Đinh Thị Mai

CHƯƠNG 2:
PHÂN TÍCH HỆ THỐNG
TRONG MIỀN THỜI GIAN
2.1 Hệ thống liên tục
• Phương trình vi phân của hệ thống LTI liên tục
• Biểu diễn hệ thống bằng đáp ứng xung
• Mô hình biến trạng thái
Phương trình vi phân của hệ thống LTI
• Phương trình vi phân là loại mô hình toán học được
sử dụng phổ biến nhất để biểu diễn các hệ thống trong
nhiều lĩnh vực khác nhau
• Đối với các hệ thống vật lý, phương trình vi phân
biểu diễn hệ thống được thiết lập từ các phương trình
của các định luật vật lý mà hoạt động của hệ thống
tuân theo
• Các hệ thống LTI được biểu diễn bởi các phương
trình vi phân tuyến tính hệ số hằng
Một ví dụ của một hệ thống biểu diễn bằng phương trình vi
phân hệ số hằng
Phương trình vi phân của hệ thống LTI
• Dạng tổng quát của các phương trình vi phân tuyến
tính hệ số hằng biểu diễn các hệ thống tuyến tính bất
biến:
với x(t) là tín hiệu lối vào, y(t) là tín hiệu lối ra của hệ thống
• Giải phương trình vi phân tuyến tính nói trên cho
phép xác định tín hiệu ra y(t) theo tín hiệu vào x(t)
0 0
( ) ( )
i jN M
i ji j
i j
d y t d x t
a b
dt dt
Phương trình vi phân của hệ thống LTI
• Nghiệm của phương trình vi phân tuyến tính hệ số
hằng có dạng như sau:
y0(t): đáp ứng khởi đầu, còn gọi là đáp ứng khi không có kích
thích, là nghiệm của phương trình thuần nhất
(1)
ys(t): đáp ứng ở trạng thái không, là nghiệm đặc biệt của
phương trình đối với tín hiệu vào x(t)
0
( ) ( ) ( )
s
y t y t y t
0
( )
0
iN
i i
i
d y t
a
dt
Phương trình vi phân của hệ thống LTI
• y0(t) là đáp ứng của hệ thống đối với điều kiện của
hệ thống tại thời điểm khởi đầu (t=0), không xét tới tín
hiệu vào x(t)
• Phương trình thuần nhất (1) có nghiệm dạng est với s
là biến phức, thay vào phương trình ta có:
→ s là nghiệm của phương trình đại số tuyến tính bậc N sau:
0
0
N
i st
i
i
a s e
0
0
N
i
i
i
a s
(2)
Phương trình vi phân của hệ thống LTI
• Phương trình (2) được gọi là phương trình đặc trưng
của hệ thống
• Gọi các nghiệm của (2) là {sk|k=1N}, nghiệm tổng
quát của phương trình thuần nhất (1) sẽ có dạng như
sau nếu các nghiệm {sk} đều là nghiệm đơn:
Giá trị của các hệ số {ck} được xác định từ các điều
kiện khởi đầu
0
1
( ) k
N
s t
k
k
y t c e
Phương trình vi phân của hệ thống LTI
• Trường hợp phương trình (2) có nghiệm bội thì
nghiệm tổng quát của phương trình thuần nhất (1) sẽ
có dạng như sau:
trong đó pk là bội của nghiệm sk
1
0
0
( ) ( )
k
k
p
s t i
k
k i
y t c e t
Phương trình vi phân của hệ thống LTI
• ys(t) là đáp ứng của hệ thống đối với tín hiệu vào
x(t) khi các điều kiện khởi đầu đều bằng 0
• ys(t) còn được gọi là nghiệm đặc biệt của phương
trình vi phân tuyến tính biểu diễn hệ thống
• Để xác định ys(t), thông thường giả thiết ys(t) có
dạng tương tự tín hiệu vào x(t) với một vài hệ số chưa
biết, sau đó thay vào phương trình để xác định các hệ
số.
Phương trình vi phân của hệ thống LTI
• Chú ý khi giả thiết dạng của ys(t): ys(t) phải độc lập
với tất cả các thành phần của y0(t)
• Ví dụ: nếu x(t)=eαt, ta có thể gặp một số trường hợp
như sau:
• Nếu eαt không phải là một thành phần của y0(t), ta có thể
giả thiết ys(t) có dạng ce
αt
• Nếu α là một nghiệm đơn của phương trình đặc trưng (2)
→ eαt là một thành phần của y0(t)→ys(t) phải có dạng cte
αt
• Nếu α là một nghiệm bội bậc p của phương trình đặc trưng
(2) → eαt, → teαt,, → tp-1eαt là các thành phần của
y0(t)→ys(t) phải có dạng ct
peαt
Biểu diễn hệ thống bằng đáp ứng xung
• Định nghĩa tích chập của hai tín hiệu: f(t) và g(t), ký
hiệu là f(t)*g(t), được định nghĩa như sau:
( )* ( ) ( ) ( )f t g t f g t d
Biểu diễn hệ thống bằng đáp ứng xung
• Các tính chất của tích chập:
• Tính giao hoán:
f(t)*g(t)=g(t)*f(t)
• Tính kết hợp:
[f(t)*g(t)]*h(t)=f(t)*[g(t)*h(t)]
• Tính phân phối:
[f(t)+g(t)]*h(t)=f(t)*h(t)+g(t)*h(t)
Biểu diễn hệ thống bằng đáp ứng xung
• Tính dịch thời gian: nếu x(t)=f(t)*g(t) thì
x(t-t0) = f(t-t0)*g(t) = f(t)*g(t-t0)
• Tính nhân chập với tín hiệu xung đơn vị
f(t)*δ(t)=f(t)
• Tính nhân quả: nếu f(t) và g(t) là các tín hiệu nhân quả thì
f(t)*g(t) cũng là tín hiệu nhân quả
Biểu diễn hệ thống bằng đáp ứng xung
• Đáp ứng xung của hệ LTI:
• Cho một hệ thống LTI được biểu diễn bằng mối quan hệ
y(t) = T[x(t)]. Ta có thể biến đổi biễu diễn đó như sau:
trong đó h(t) = T[δ(t)] được gọi là đáp ứng xung của hệ LTI
biểu diễn bởi T
• Một hệ thống LTI là xác định khi đáp ứng xung của hệ
thống đó xác định
( ) [x(t)* (t)]= ( ) ( )
( ) [ ( )] ( )* ( )
y t x t d
x t d x t h t
Τ T
T
Biểu diễn hệ thống bằng đáp ứng xung
• Phân tích đáp ứng xung của hệ LTI:
• Hệ thống tĩnh: đáp ứng xung chỉ có giá trị khác không tại t
= 0
• Hệ thống nhân quả: đáp ứng xung là tín hiệu nhân quả
• Hệ thống ổn đinh: khi và chỉ khi điều kiện sau đây đối với
đáp ứng xung được thỏa mãn:
| ( ) |h t dt
Biểu diễn hệ thống bằng đáp ứng xung
• Đáp ứng xung của các hệ thống ghép nối
• Ghép nối tiếp hai hệ thống
Đáp ứng xung tổng hợp: h(t) = h1(t)*h2(t)
• Ghép song song hai hệ thống
Đáp ứng xung tổng hợp: h(t) = h1(t) + h2(t)
Biến trạng thái của hệ thống
• Trạng thái của một hệ thống được mô tả bằng một
tập hợp các biến trạng thái
• Mô hình biến trạng thái của một hệ thống tuyến tính
bất biến là tập hợp các phương trình vi phân của các
biến trạng thái, cho phép xác định trạng thái trong
tương lai của hệ thống khi biết trạng thái hiện thời và
tín hiệu vào, do đó hệ thống hoàn toàn xác định khi
trạng thái khởi đầu của hệ thống là xác định
• Mô hình biến trạng thái rất thuận tiện để biểu diễn hệ
thống đa biến
Biến trạng thái của hệ thống
• Gọi {u1(t), u2(t),,} là các tín hiệu vào, {y1(t),
y2(t),,} là các biến ra và {q1(t), q2(t),,} là các biến
trạng thái của hệ LTI.
• Phương trình trạng thái của hệ thống là các phương
trình vi phân tuyến tính bậc nhất:
• Các tín hiệu ra được xác định từ biến trạng thái và
các tín hiệu vào như sau:
ij ik
( )
( ) ( ) ( 1,2...)i
j k
j k
dq t
a q t k u t i
dt
ij ik
( ) ( ) ( ) ( 1,2...)
i j k
j k
y t c q t d u t i
Biến trạng thái của hệ thống
• Mô hình trạng thái của một hệ thống tuyến tính bất
biến thường được biểu diễn dưới dạng ma trận như
sau:
trong đó: u(t), y(t), q(t) là vecto cột với các phần tử
lần lượt là các tín hiệu vào, tín hiệu ra và các biến
trạng thái của hệ thống. A,B,C,D là các ma trận hệ số
( )
( ) ( )
( ) ( ) ( )
d t
t t
dt
t t t
q
Aq Bu
y Cq Du
Biến trạng thái của hệ thống
• Thiết lập phương trình trạng thái từ phương trình vi
phân biểu diễn hệ thống LTI sau đây:
• Đặt uj(t) = d
jx(t)/dtj (j=0M) là các tín hiệu vào của
hệ thống và viết lại phương trình trên dưới dạng:
0 0
( ) ( )
i jN M
i ji j
i j
d y t d x t
a b
dt dt
0 0
( )
( )
iN M
i j ji
i j
d y t
a b u t
dt
Biến trạng thái của hệ thống
• Chọn các biến trạng thái như sau:
• Các phương trình trạng thái
1
1 2 1
( ) ( )
( ) ( ), ( ) ,..., ( )
N
N N
dy t d y t
q t y t q t q t
dt dt
1 2 1
2 3
1
1
0 0
( ) ( ) ( )
( ), ( ),..., ( )
( ) 1
( ) ( )
N
N
N M
N
i i j j
i jN
dq t dq t dq t
q t q t q t
dt dt dt
dq t
aq t b u t
dt a
File đính kèm:
 bai_giang_tin_hieu_va_he_thong_chuong_2_phan_1_phan_tich_he.pdf
bai_giang_tin_hieu_va_he_thong_chuong_2_phan_1_phan_tich_he.pdf

