Bài giảng Tín hiệu và hệ thống - Chương 1: Giới thiệu tín hiệu và hệ thống - Đinh Thị Mai

CHƯƠNG 1: 
GIỚI THIỆU TÍN HIỆU VÀ 
HỆ THỐNG 
GV: ThS. Đinh Thị Thái Mai 
1.1. TÍN HIỆU 
• Định nghĩa tín hiệu 
• Phân loại tín hiệu 
• Các phép toán cơ bản trên tín hiệu 
• Các tín hiệu cơ bản 
 Định nghĩa tín hiệu: 
• Một đại lượng vật lý truyền tải thông tin về bản 
chất của một hiện tượng vật lý 
• Có thể biểu diễn dưới dạng hàm thời gian liên tục 
hoặc rời rạc 
• Hàm của một hay nhiều biến: 
• Tín hiệu âm thanh: hàm của thời gian (tín hiệu một 
chiều) 
• Ảnh động: (phép chiếu của của một cảnh động vào mặt 
phẳng ảnh): hàm của 3 biến x,y,t (tín hiệu nhiều chiều) 
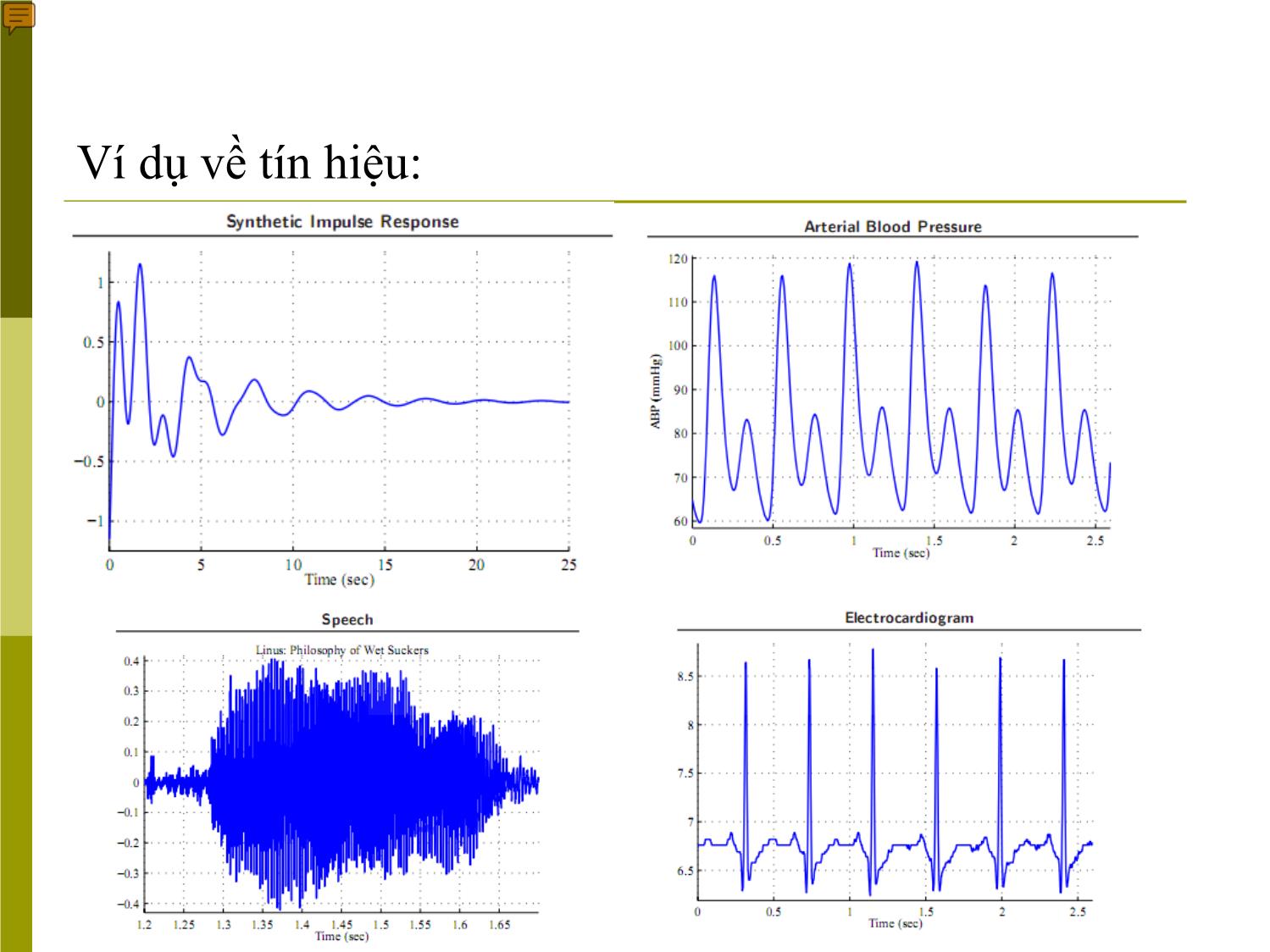
 Ví dụ về tín hiệu: 
 Phân loại tín hiệu 
• Tín hiệu liên tục và rời rạc 
• Tín hiệu tương tự và số 
• Tín hiệu tuần hoàn và không tuần hoàn 
• Tín hiệu nhân quả và không nhân quả 
• Tín hiệu chẵn và lẻ 
• Tín hiệu xác định và ngẫu nhiên 
• Tín hiệu đa kênh và đa chiều 
• Tín hiệu bên trái và phải 
• Tín hiệu hữu hạn và vô hạn 
• Tín hiệu năng lượng và công suất 
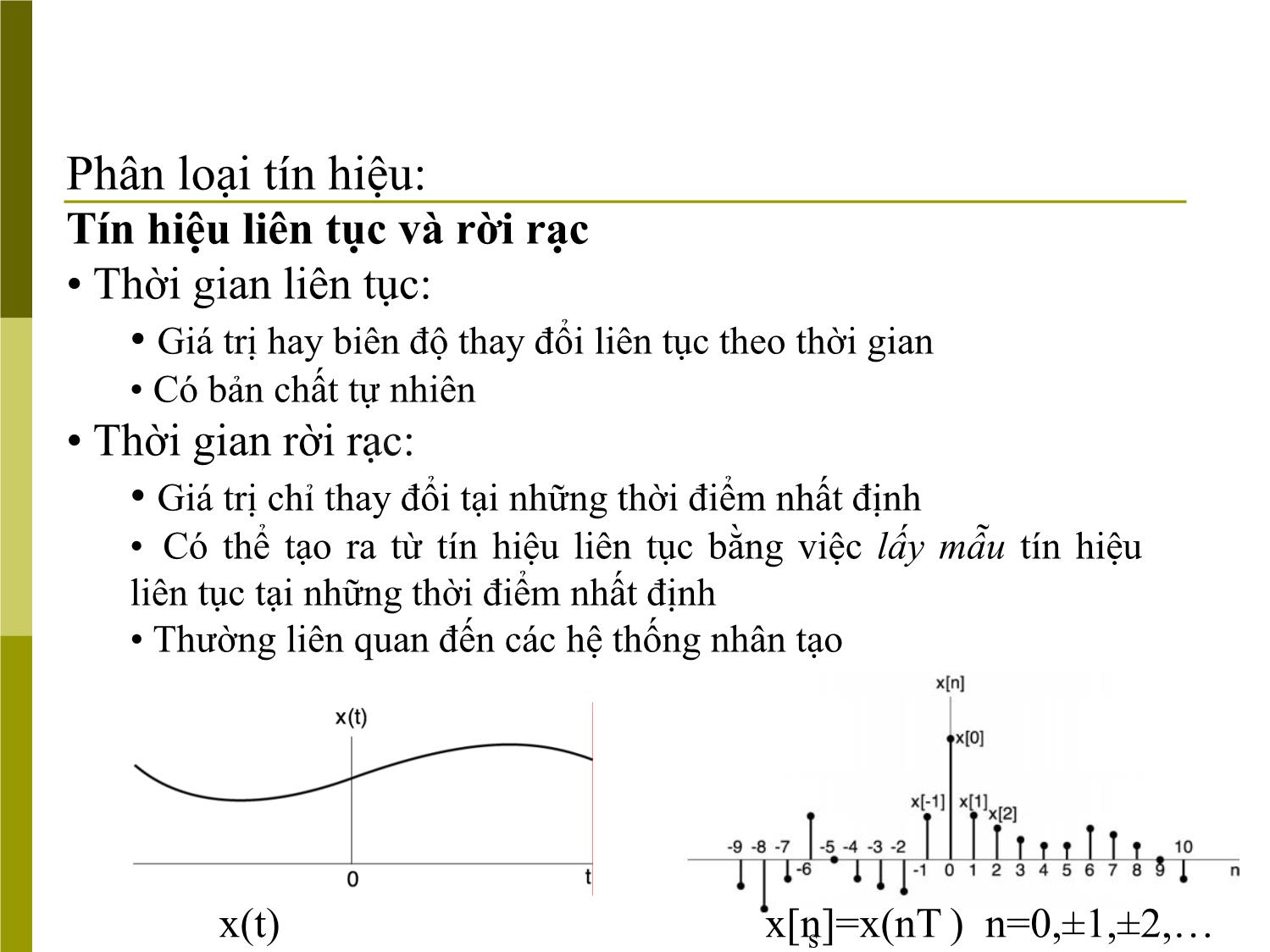
 Phân loại tín hiệu: 
Tín hiệu liên tục và rời rạc 
• Thời gian liên tục: 
• Giá trị hay biên độ thay đổi liên tục theo thời gian 
• Có bản chất tự nhiên 
• Thời gian rời rạc: 
• Giá trị chỉ thay đổi tại những thời điểm nhất định 
• Có thể tạo ra từ tín hiệu liên tục bằng việc lấy mẫu tín hiệu 
liên tục tại những thời điểm nhất định 
• Thường liên quan đến các hệ thống nhân tạo 
x(t) x[n]=x(nTs ) n=0,±1,±2, 
 Phân loại tín hiệu: 
• Giá trị liên tục: Giá trị của tín hiệu thay đổi một cách 
liên tục 
• Giá trị rời rạc: giá trị của tín hiệu thay đổi không liên 
tục 
Tín hiệu tương tự và số 
• Tín hiệu tương tự: tín hiệu liên tục theo thời gian và có 
giá trị liên tục 
• Tín hiệu số: tín hiệu rời rạc theo thời gian và có giá trị 
được lượng tử hóa hay có giá trị rời rạc 
 Phân loại tín hiệu: 
Tín hiệu tuần hoàn và không tuần hoàn 
• Tín hiệu tuần hoàn: lặp lại chính bản thân tín hiệu sau một 
khoảng thời gian nhất định 
 x(t)=x(t+T) với mọi T>0 
 hay x[n]=x[n+N] với N nguyên dương 
• Chu kỳ cơ bản của tín hiệu tuần hoàn là giá trị nhỏ nhất của T 
 thỏa mãn điều kiện trên (T hay N) 
• Tần số cơ bản = 1/chu kỳ cơ bản (f=1/T hay f=1/N) 
• Tần số góc cơ bản = 2π*tần số cơ bản (ω = 2π/T rad/s hay Ω= 2π/N 
rad) 
• Tín hiệu không tuần hoàn: không có giá trị nào của T thỏa 
mãn điều kiện trên hay giá trị của tín hiệu không được lặp 
lại một cách có chu kỳ 
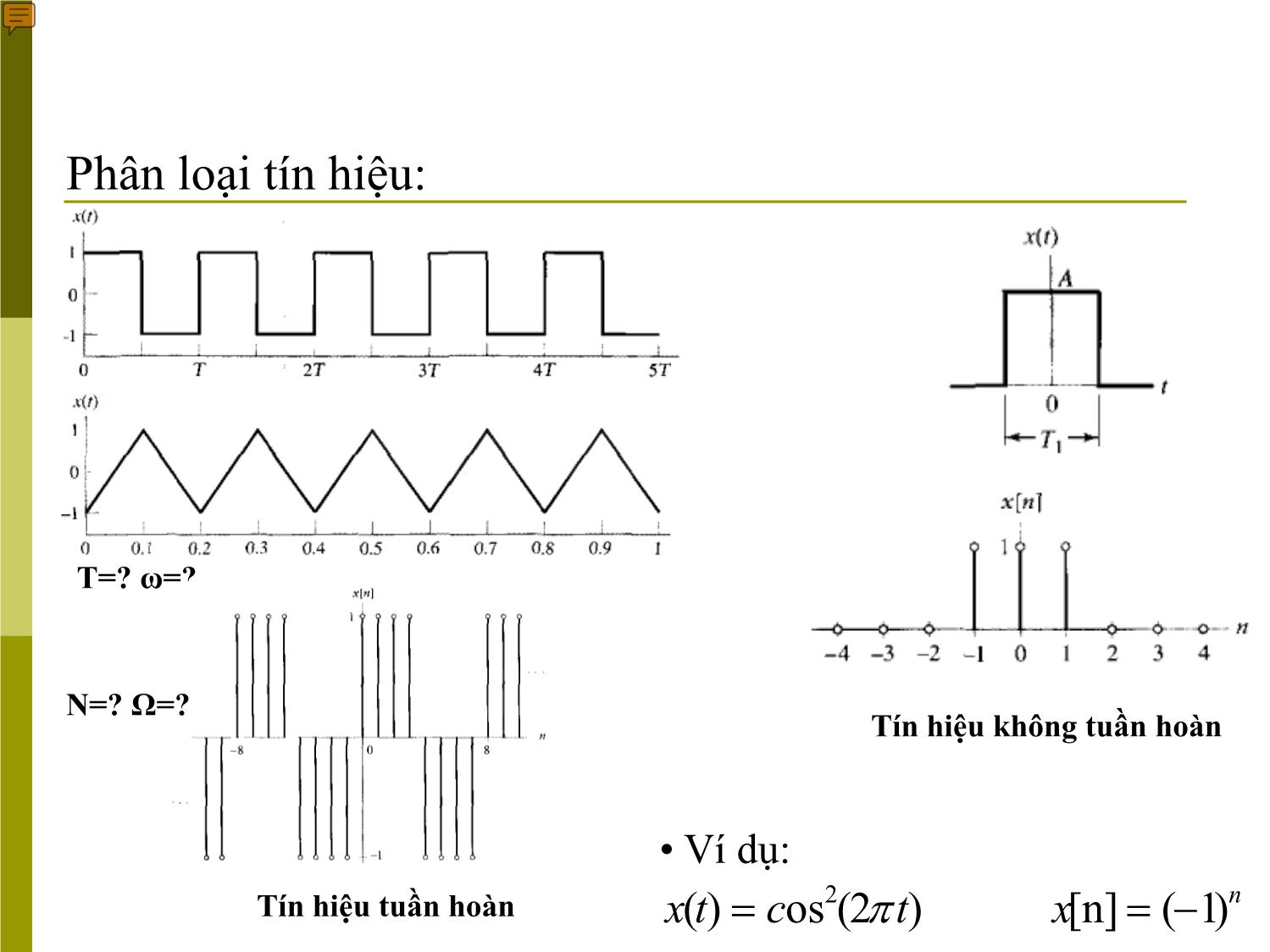
 Phân loại tín hiệu: 
T=? ω=? 
N=? Ω=? 
Tín hiệu tuần hoàn 
Tín hiệu không tuần hoàn 
• Ví dụ: 
2( ) os (2 ) [n] ( 1)nx t c t xπ= = −
 Phân loại tín hiệu: 
Tín hiệu nhân quả và không nhân quả 
• Tín hiệu nhân quả: giá trị của tín hiệu luôn bằng không 
trên phần âm của trục thời gian 
• Tín hiệu phản nhân quả: giá trị của tín hiệu luôn bằng 
không trên phần dương của trục thời gian 
• Tín hiệu phi (không) nhân quả: tín hiệu có giá trị khác 
không trên cả phần âm và phần dương của trục thời gian 
 Phân loại tín hiệu: 
• Ví dụ: 
0 : ( ) 0t f t∀ < = : ( ) 0t f t∀ ≠
Tín hiệu nhân quả Tín hiệu phi nhân quả Tín hiệu phản nhân quả 
0 : ( ) 0t f t∀ > =
 Phân loại tín hiệu: 
Tín hiệu chẵn và lẻ 
• Tín hiệu chẵn: x(t) = x(-t) hay x[n]=x[-n] 
• Tín hiệu lẻ: x(-t) = -x(t) hay x[-n]=-x[n] 
• Bất kỳ một tín hiệu nào có thể được biểu diễn như là tổng 
của một tín hiệu chẵn và một tín hiệu lẻ 
 x(t)=xe(t)+xo(t) 
Trong đó: 
sin( ),
( )
0, ác
( ) cos( ) sin( ) sin( ) os( )
t T t T
x t T
t kh
x t t t t c t
π − ≤ ≤= 

= + + Tín hiệu chẵn 
Tín hiệu lẻ 
• Ví dụ 
1( ) ( ) ( )2
1( ) ( ) ( )2
x t x t x te
x t x t x to
 
 
 
 
= + −
= − −
 Phân loại tín hiệu: 
Tín hiệu xác định và ngẫu nhiên 
• Tín hiệu xác định: được mô hình như là một hàm của thời 
gian, vì thế giá trị của tín hiệu tại bất kỳ thời điểm nào đều có 
thể tính trước được bằng biểu thức toán học hoặc bảng giá trị 
• Tín hiệu ngẫu nhiên: nhiều yếu tố không chắc chắn xuất 
hiện trước khi tín hiệu xuất hiện, do đó không xác định được 
chính xác giá trị tại một thời điểm trong tương lai. 
Tín hiệu xác định Tín hiệu ngẫu nhiên 
 Phân loại tín hiệu: 
Tín hiệu đa kênh và đa chiều 
• Tín hiệu đa kênh: thường được biểu diễn dưới dạng một 
véctơ trong đó các thành phần của véctơ là các tín hiệu đơn 
kênh: 
 F(t) = [ f1(t) f2(t).fN(t)] 
• Tín hiệu đa chiều: thường được biểu diễn dưới dạng hàm 
của nhiều biến độc lập: 
f(x1,x2,xN) 
 Phân loại tín hiệu: 
Tín hiệu thuận và nghịch 
• Tín hiệu thuận (bên phải): giá trị của tín hiệu luôn bằng 0 
kể từ một thời điểm về trước, nghĩa là 
• Tín hiệu nghịch (bên trái): giá trị của tín hiệu luôn bằng 0 
kể từ một thời điểm trở về sau, nghĩa là 
0 : ( ) 0t t x t∀ < < ∞ =
0 : ( ) 0t t x t∀ > > −∞ =
 Phân loại tín hiệu: 
Tín hiệu hữu hạn và vô hạn 
• Tín hiệu hữu hạn: tất cả các giá trị khác không của tín hiệu 
đều nằm trong một khoảng hữu hạn, ngoài khoảng đó giá trị 
của tín hiệu luôn bằng 0, nghĩa là tồn tại một khoảng hữu 
hạn sao cho 
• Tín hiệu vô hạn: không tồn tại khoảng hữu hạn thỏa mãn 
điều kiện trên hay miền các giá trị khác không của tín hiệu 
là vô hạn 
1 2 1 2: ( ) 0 [t ,t ]t t f t khi t−∞ < < < ∞ = ∉
 Tín hiệu năng lượng và tín hiệu công suất 
• Năng lượng của một tín hiệu liên tục x(t) và rời rạc x[n] 
được định nghĩa bởi: 
• Một tín hiệu là tín hiệu năng lượng khi nó có năng lượng 
hữu hạn, nghĩa là thỏa mãn: 
0<E<∞ 
• Tín hiệu tuần hoàn không phải là tín hiệu năng lượng do 
năng lượng của tín hiệu tuần hoàn là vô hạn 
• Tín hiệu xác định có độ dài hữu hạn là các tín hiệu năng 
lượng 
2( )xE x t dt
∞
−∞
= ∫
2[ ]x
n
E x n
∞
=−∞
= ∑
 Tín hiệu năng lượng và tín hiệu công suất 
• Công suất của một tín hiệu được định nghĩa là năng lượng 
trung bình của tín hiệu trong một đơn vị thời gian 
• Công suất của tín hiệu liên tục x(t) và rời rạc x[n] được 
định nghĩa như sau: 
/2
2
/2
1lim ( )
T
x T
T
P x t dt
T→∞ −
= ∫
21lim [ ]
2
N
x N n N
P x n
N→∞ =−
= ∑
 Tín hiệu năng lượng và tín hiệu công suất 
/2
2
/2
1 ( )
T
x
T
P x t dt
T −
= ∫
1
2
0
1 [ ]
N
x
n
P x n
N
−
=
= ∑
• Công suất của tín hiệu liên tục tuần hoàn x(t) với chu kỳ T 
và thời gian rời rạc x[n] với chu kỳ N là tương đương với 
năng lượng trung bình trong một chu kỳ nên công suất 
trung bình của tín hiệu tuần hoàn được định nghĩa là: 
• Một tín hiệu là tín hiệu công suất khi nó có công suất trung 
bình hữu hạn, nghĩa là thỏa mãn: 
0<P<∞ 
 Tín hiệu năng lượng và tín hiệu công suất 
• Một tín hiệu nếu là tín hiệu năng lượng thì không thể là tín 
hiệu công suất do công suất của tín hiệu năng lượng luôn 
bằng 0 
• Một tín hiệu nếu là tín hiệu công suất thì không thể là tín 
hiệu năng lượng do năng lượng của tín hiệu công suất luôn 
vô hạn, ví dụ đối với tín hiệu tuần hoàn 
• Ví dụ: xác định năng lượng và công suất trung bình của tín 
hiệu sau: 
0 1
os( ) 0
( ) 2 1 2 [ ]
0 ác
0 ác
t t
c n n
x t t t x n
kh
kh
π
≤ ≤
≥= − ≤ ≤ = 


 Các phép toán cơ bản trên tín hiệu 
• Phép toán trên biến phụ thuộc 
• Phép toán trên biến độc lập 
 Phép toán trên các biến phụ thuộc 
• Tỷ lệ: y(t) = cx(t), 
 y[n] = cx[n], c: hệ số tỷ lệ 
• Cộng tín hiệu: y(t) = x1(t) + x2(t) 
 y[n] = x1[n] + x2[n] 
• Nhân tín hiệu: y(t) = x1(t) x2(t) 
 y[n] = x1[n] x2[n] 
• Vi phân tín hiệu: 
• Tích phân tín hiệu: 
( )( ) dx ty t
dt
=
( ) ( )
t
y t x t
−∞
= ∫
 Phép toán trên các biến độc lập 
• Tỷ lệ thời gian y(t) = x(at) 
• a>1: nén tín hiệu 
• 0<a<1: giãn tín hiệu 
y[n]=x[kn] , k>0 
• k>1: mất giá trị 
 Phép toán trên các biến độc lập 
• Phép lật: thay t = -t hoặc n = -n 
 y(t) = x(-t) 
• Phép lật tín hiệu chẵn là chính nó 
• Phép lật tín hiệu lẻ là giá trị âm của chính nó 
• Ví dụ: xác định tín hiệu hợp y[n]=x[n]+x[-n] của 
1 1
1 1& 1
[ ] 1 1 [ ]
0 0& | | 1
0 0&|n|>1
n
n n
x n n x n
n n
n
=
= − == − = − =  = > =
 Phép toán trên các biến độc lập 
• Dịch thời gian: y(t) = x(t - t0) 
• t0>0: dịch sang phải (trễ) 
• t0<0: dịch sang trái (tiến) 
y[n] = x[n-m] 
• m: nguyên dương hoặc nguyên âm 
 • Ví dụ: tìm tín hiệu dịch thời gian y[n]=x[n+3] của: 
1 1,2
[ ] 1 1, 2
0 0& | | 2
n
x n n
n n
=
= − = − −
 = >
 Một số tín hiệu cơ bản 
• Tín hiệu xung 
• Tín hiệu xung đơn vị thời gian liên tục, ký hiệu là δ(t), 
được định nghĩa bằng hàm delat Dirac như sau: 
• Tín hiệu xung đơn vị thời gian rời rạc, ký hiệu δ[n], 
được định nghĩa bởi 
0 0
( )
0 0
t
t
t
δ
≠
= ≠ =
( ) 1t dtδ
∞
−∞
=∫
0 0
[ ]
1 0
n
n
n
δ
≠
=  =
 • Tín hiệu nhảy bậc 
• Tín hiệu nhẩy bậc đơn vị thời gian liên tục, ký hiệu 
u(t), được định nghĩa như sau: 
• Tín hiệu nhẩy bậc đơn vị thời gian rời rạc, ký hiệu u[n], 
được định nghĩa như sau: 
0 0
( )
1 0
t
u t
t
<
=  ≥
0 0
[ ]
1 0
n
u n
n
<
=  ≥
Một số tín hiệu cơ bản 
 • Tín hiệu dốc 
• Tín hiệu dốc thời gian liên tục, ký hiệu r(t), được định 
nghĩa như sau: 
• Tín hiệu dốc thời gian rời rạc, ký hiệu r[n], được định 
nghĩa như sau: 
 tương đương r(t)=tu(t), r[n]=tu[n] 
0 0
( )
0
t
r t
t t
<
=  ≥
0 0
[ ]
0
n
r n
n n
<
=  ≥
Một số tín hiệu cơ bản 
• Tín hiệu sin 
• Tín hiệu sin giá trị thực thời gian liên tục được biểu 
diễn dưới dạng sau: 
s(t) = Acos(ωt+φ) 
A: biên độ, ω: tần số góc (rad/s), φ: góc pha (rad). Chu 
kỳ của tín hiệu tuần hoàn này là T=2π/ω 
• Có thể biểu diễn dưới dạng là hàm của biến tần số 
f=1/T (Hz): 
s(t) = Acos(2πft+φ) 
Một số tín hiệu cơ bản 
• Tín hiệu sin giá trị thực thời gian rời rạc được biểu diễn 
dưới dạng sau: 
s[n] = Acos(Ωt+φ) 
A: biên độ, Ω : tần số góc (rad/chu kỳ), φ: góc pha (rad). 
• Tín hiệu thời gian rời rạc này có thể là tuần hoàn hoặc 
không. Nếu tuần hoàn với chu kỳ N thì phải thỏa mãn điều 
kiện ΩN=2πm, m: số nguyên 
Một số tín hiệu cơ bản 
 • Tín hiệu mũ thực 
• Tín hiệu mũ thực thời gian liên tục được định nghĩa 
như sau: 
f(t) = Aeαt 
A và α là các giá trị thực 
• Nếu α>0: f(t) mũ tăng, α<0: f(t) mũ giảm 
Một số tín hiệu cơ bản 
 • Tín hiệu mũ thực thời gian rời rạc được định nghĩa như 
sau: 
f[n] = Arn, r = eα 
• Nếu 01: f[n] mũ tăng 
Một số tín hiệu cơ bản 
• Tín hiệu mũ phức 
• Tín hiệu mũ phức thời gian liên tục được định nghĩa 
như sau: 
f(t) = Ae(σ+jω)t 
• Mối liên quan giữa tín hiệu mũ và tín hiệu sin: sử dụng 
biểu thức Euler cho ejωt, ta thu được biểu thức sau cho tín 
hiệu mũ phức: 
f(t) = Aeσt[cos(ωt)+jsin(ωt)] 
Một số tín hiệu cơ bản 
• f(t) là một hàm giá trị phức trong đó phần thực và phần 
ảo được tính như sau: 
Re[f(t)] = Aeσtcos(ωt) 
Im[f(t)] = Aeσtsin(ωt) 
• f(t) cũng được gọi là tín hiệu sin phức với độ lớn phức 
là Aeσt và tần số góc ω 
f(t) = Ae(σ+jω)t 
• Độ lớn thực của f(t) là |A|eσt và pha là φ: 
2 2 Im( )| | Re( ) Im( ) , arctan
Re( )
AA A A
A
ϕ= + =
Một số tín hiệu cơ bản 
1.2. HỆ THỐNG 
 • Định nghĩa hệ thống 
• Mô hình toán học của hệ thống 
• Một số ví dụ về hệ thống 
• Phân loại và đặc điểm của hệ thống 
 Định nghĩa hệ thống 
• Một hệ thống là một thực thể hoạt động khi có tín hiệu lối 
vào (kích thích) và sinh ra tín hiệu lối ra (đáp ứng) 
• Theo biểu diểu toán học, hệ thống được đặc trưng bởi mối 
quan hệ giữa tín hiệu lối vào và tín hiệu lối ra 
y(t) = T[x(t)] 
y[n] = T{x[n]} 
 T: phép biến đổi đặc trưng cho hệ thống 
x(t) T y(t) x[n] T y[n] 
 Mô hình toán học của hệ thống 
• Mối quan hệ giữa lối vào của hệ thống và lối ra của hệ 
thống, còn gọi là hành vi của hệ thống, được biểu diễn bằng 
một mô hình toán học 
• Mô hình toán học cho phép xác định hệ thống: xác định 
tín hiệu lối ra khi biết tín hiệu lối vào 
• Mô hình toán học được sử dụng trong việc phân tích và 
thiết kế hệ thống 
 Ví dụ về hệ thống 
Hệ thống truyền thông tương tự 
 Ví dụ về hệ thống 
Hệ thống truyền thông số 
 Ví dụ về hệ thống 
Hệ thống điều khiển phản hồi 
 Phân loại hệ thống 
• Hệ thống liên tục và rời rạc 
• Hệ thống liên tục: các tín hiệu vào, tín hiệu ra và các tín 
hiệu sử dụng trong hệ thống đều là các tín hiệu thời gian liên 
tục 
• Hệ thống thời gian rời rạc: tín hiệu vào và tín hiệu ra là các 
tín hiệu thời gian rời rạc 
 Phân loại hệ thống 
• Hệ thống đơn biến và hệ thống đa biến 
• SISO: (Single-input Single output): một biến vào-một biến ra 
• SIMO: (Single input Multiple ouput): một biến vào-nhiều biến ra 
• MISO: (Multiple input Single output): nhiều biến vào-một biến ra 
• MIMO: (Multiple input Multiple output): nhiều biến vào- nhiều 
biến ra 
 Phân loại hệ thống 
• Hệ thống tĩnh và động (nhớ và không nhớ) 
• Một hệ thống khi lối ra của hệ thống chỉ phụ thuộc vào giá trị 
của tín hiệu vào tại cùng một thời điểm được gọi là hệ thống tĩnh 
hay hệ thống không nhớ 
• Một hệ thống khi lối ra của hệ thống phụ thuộc cả vào giá trị 
trong quá của tín hiệu vào được gọi là hệ thống động hay hệ 
thống có nhớ 
2
1( ) ( )
[ ] [ ]
i t v t
R
y n x n
=
=
1( ) ( )
1[ ] ( [ ] [ 1] [ 2])
3
t
i t v d
L
y n x n x n x n
τ τ
−∞
=
= + − + −
∫
 Phân loại hệ thống 
• Hệ thống nhân quả và phi nhân quả 
• Một hệ thống nếu tín hiệu lối ra của hệ thống chỉ có thể phụ 
thuộc các giá trị của tín hiệu vào hiện tại và trong quá khứ chứ 
không thể phụ thuộc vào các giá trị tương lai của tín hiệu được 
gọi là hệ thống nhân quả. 
• Một hệ thống khi tín hiệu ra của hệ thống có thể phụ thuộc vào 
cả các giá trị tương lai của ltín hiệu vào được gọi là hệ thống 
không nhân quả 
 Phân loại hệ thống 
• Hệ thống tuyến tính 
• Hệ thống được xem là tuyến tính khi và chỉ khi thỏa mãn 
nguyên lý đồng nhất và nguyên lý xếp chồng: 
• Hệ thống không tuyến tính nếu không thỏa mãn điều kiện 
trên 
1 2 1 2, : [ ( ) ( )]= [ ( )] [ ( )]x t x t x t x tα β α β α β∀ ∈ + +R T T T
 Phân loại hệ thống 
• Hệ thống bất biến thời gian 
• Hệ thống bất biến thời gian: một sự dịch chuyển thời gian 
của tín hiệu lối vào dẫn đến sự dịch chuyển thời gian tương 
ứng ở tín hiệu lối ra → quan hệ vào/ra không phụ thuộc vào 
thời điểm bắt đầu: 
• Hệ thống thay đổi theo thời gian khi quan hệ vào/ra phụ 
thuộc vào thời điểm bắt đầu 
0 0 0( ) [ ( )] : ( ) [ ( )]y t x t t y t t x t t= Τ ⇒∀ − = Τ −
 Phân loại hệ thống 
• Hệ thống ổn định 
• Hệ thống được gọi là ổn định giới hạn BIBO (Bounded 
Input Bounded Output) khi và chỉ khi tín hiệu ra luôn có giới 
hạn hữu hạn khi tín hiệu vào có giới hạn hữu hạn 
• Nếu tín hiệu vào có giới hạn hữu hạn tạo ra một tín hiệu ra 
giới hạn không hữu hạn thì hệ thống sẽ không ổn định 
| ( ) | | ( ) |x t y t< ∞⇒ < ∞