Bài giảng Mô phỏng thiết kế hệ thống tự động - Chương 1: Khái niệm hệ thống tự động

1/2/2012 1/89
MÔ PHỎNG THIẾT KẾ
HỆ THỐNG TỰ ĐỘNG
TRƯỜNG ĐẠI HỌC GIAO THÔNG VẬN TẢI
Khoa Cơ Khí-Bộ môn Kỹ thuật máy
----------&&O&&---------
CHƯƠNG I
KHÁI NIỆM HỆ THỐNG TỰ ĐỘNG
2/89
Tài liệu tham khảo
 Lý thuyết điều khiển tự động - Nguyễn Thị Phương Hà, Huỳnh Thái
Hoàng, NXB ĐHQG TP HCM, 2003
 Automation and Control systems - Benjamin C. Kuo, Prentice-Hall
International, Ninth ediction, 2010.
 Modern Control Engineering - Katsuhiko Ogata, Prentice-Hall, Fifth
ediction, 2010.
 Control Systems Engineering - Norman S. Nise, Fifth ediction, 2008.
1/2/2012
3/89
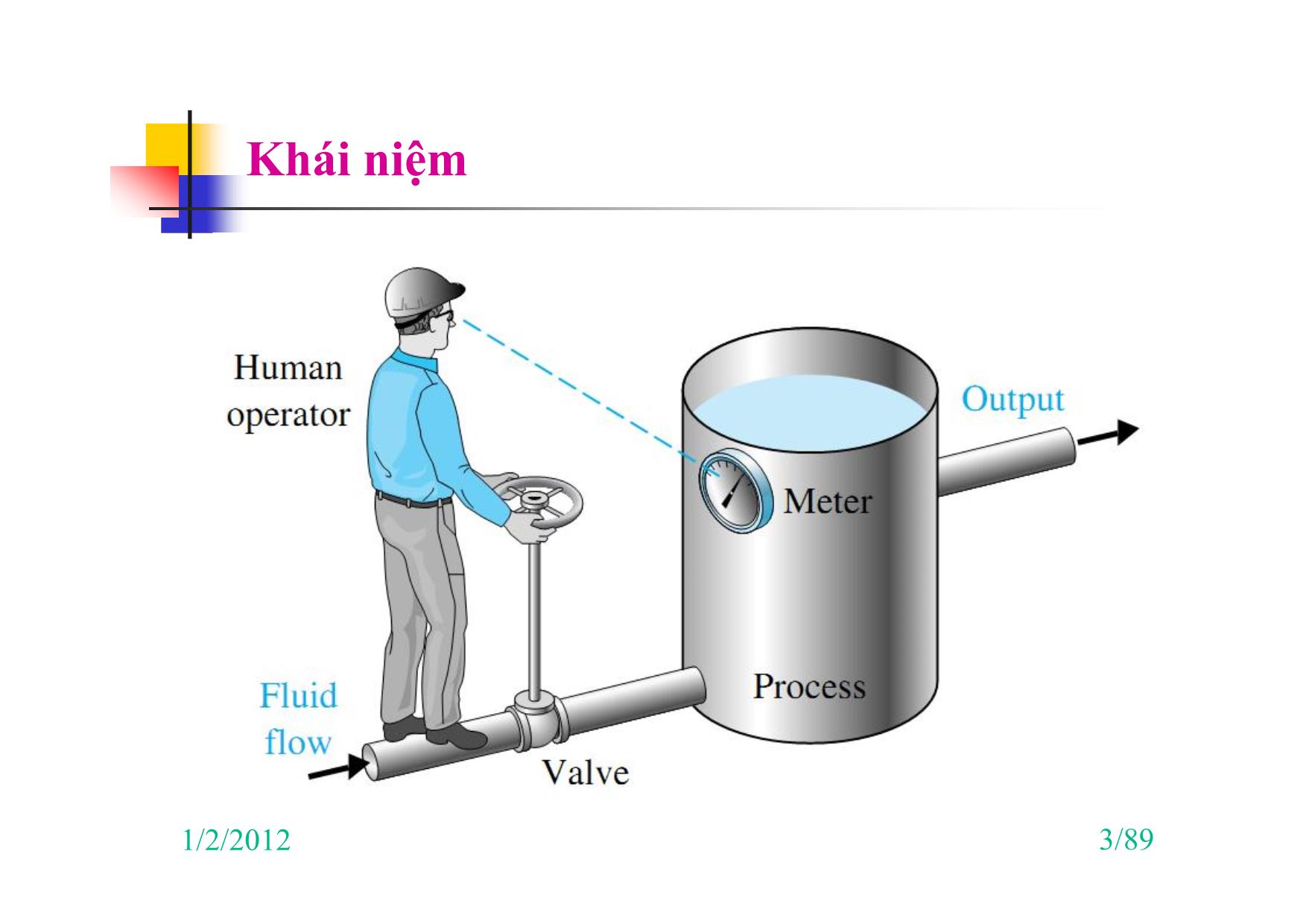
Khái niệm
1/2/2012
1/2/2012 4/89
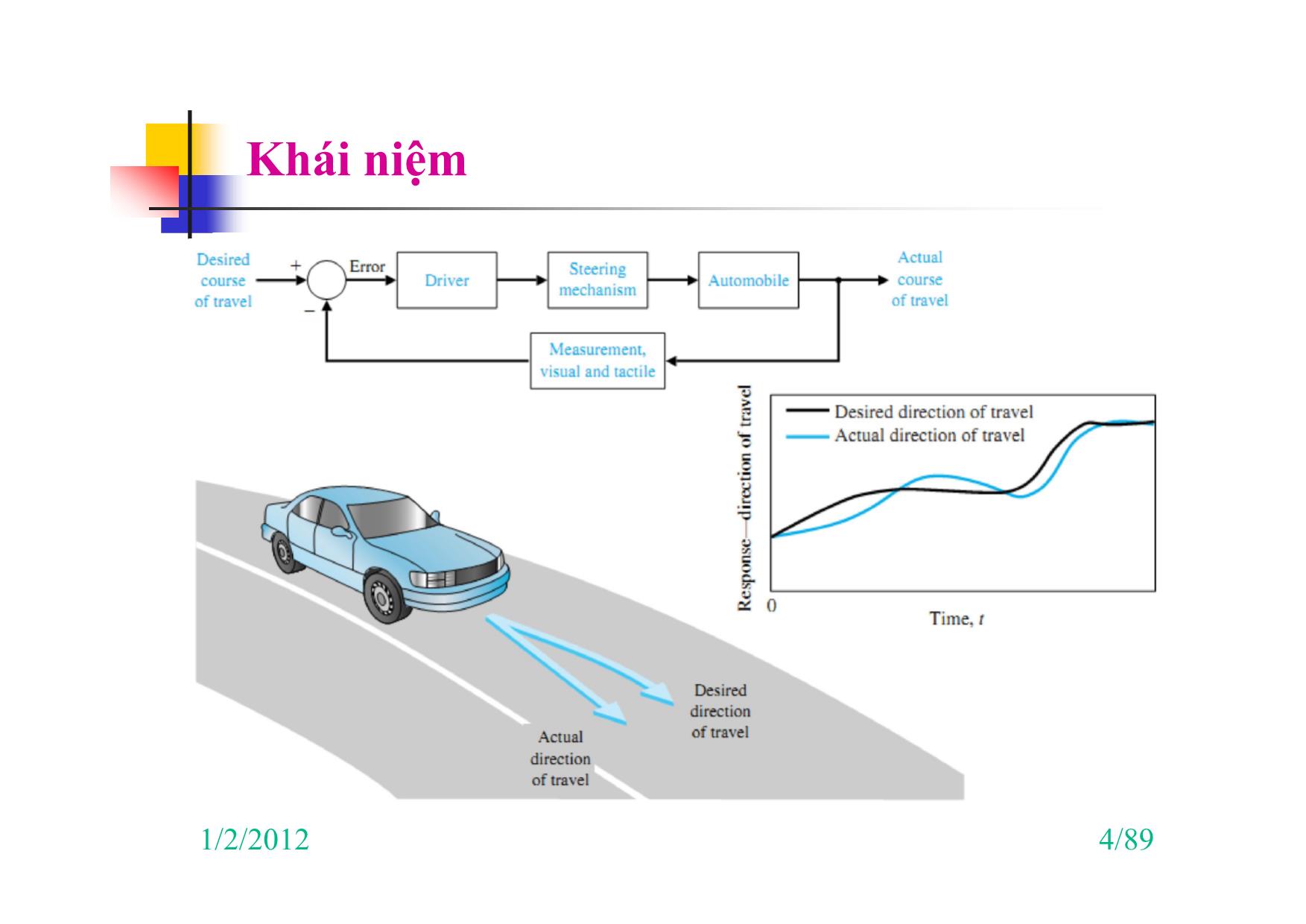
Khái niệm
1/2/2012 5/89
Định nghĩa:
Điều khiển là quá trình thu thập thông tin, xử lý thông tin, và tác động
lên hệ thống để đáp ứng của hệ thống tiến “Gần” với mục đích định trước.
Tại sao cần phải điều khiển?
 Do đáp ứng của hệ thống không thỏa mãn yêu cầu.
 Tăng độ chính xác.
 Tăng năng suất.
 Tăng hiệu quả kinh tế.
1/2/2012 6/89
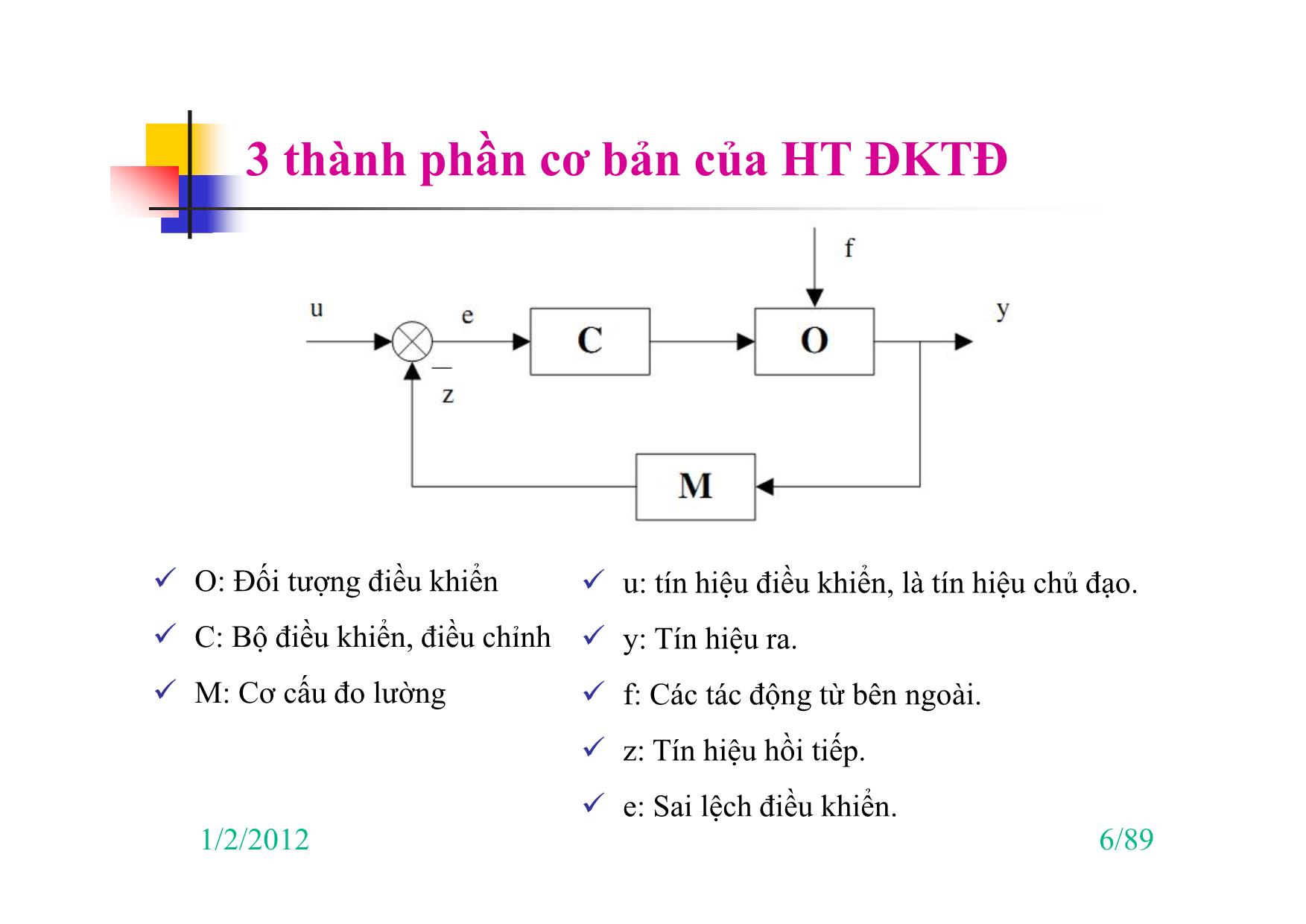
3 thành phần cơ bản của HT ĐKTĐ
 O: Đối tượng điều khiển
 C: Bộ điều khiển, điều chỉnh
 M: Cơ cấu đo lường
 u: tín hiệu điều khiển, là tín hiệu chủ đạo.
 y: Tín hiệu ra.
 f: Các tác động từ bên ngoài.
 z: Tín hiệu hồi tiếp.
 e: Sai lệch điều khiển.
1/2/2012 7/89
3 bài toán cơ bản
 Phân tích hệ thống: Cho hệ thống tự động đã biết cấu trúc và thông số.
Tìm đáp ứng của hệ thống và đánh giá chất lượng hệ thống.
 Thiết kế hệ thống: Biết cấu trúc và thông số của đối tượng điều khiển.
Thiết kế bộ điều khiển sao cho hệ thống thu được thỏa mãn các
yêu cầu về chất lượng.
 Nhận dạng hệ thống: Chưa biết cấu trúc và thông số của hệ thống.
Xác định cấu trúc và thông số của hệ thống.
1/2/2012 8/89
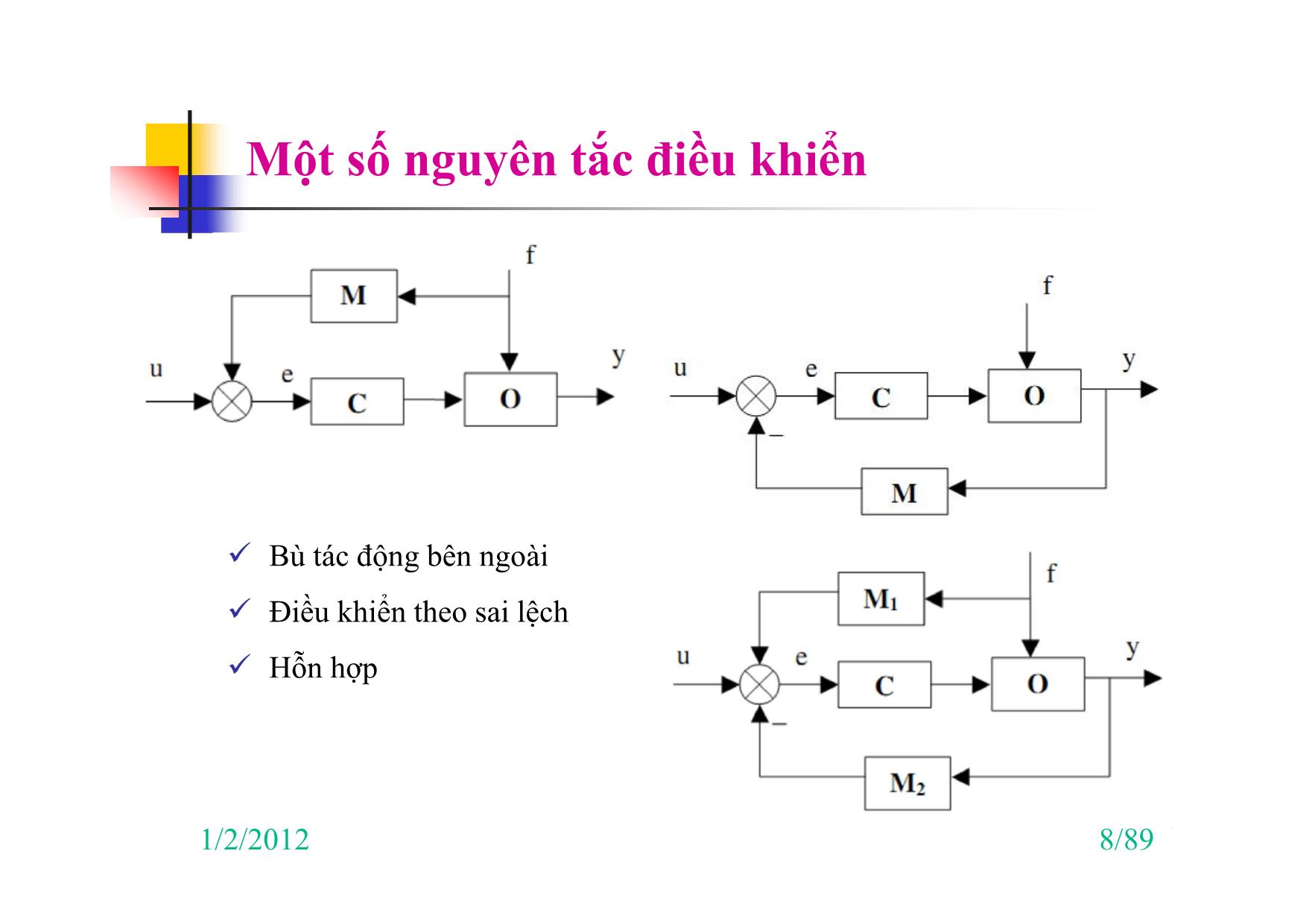
Một số nguyên tắc điều khiển
 Bù tác động bên ngoài
 Điều khiển theo sai lệch
 Hỗn hợp
1/2/2012 9/89
Phân loại hệ thống điều khiển 
Có nhiều chỉ tiêu phân loại khác nhau, tuy nhiên ta có thể kể một số loại
được phân theo mô tả toán học của hệ thống như sau:
 Hệ thống liên tục (pt vi phân)
 Hệ thống rời rạc (pt sai phân)
 Hệ thống tuyến tính (vi phân hoặc sai phân tuyến tính)
 Hệ thống phi tuyến (vi phân hoặc sai phân phi tuyến)
 Hệ thống bất biến theo thời gian (hệ số của pt vi phân hoặc sai
phân mô tả hệ thống không đổi)
 Hệ thống biến đổi theo thời gian (hệ số của pt vi phân hoặc sai
phân mô tả hệ thống thay đổi theo thời gian)
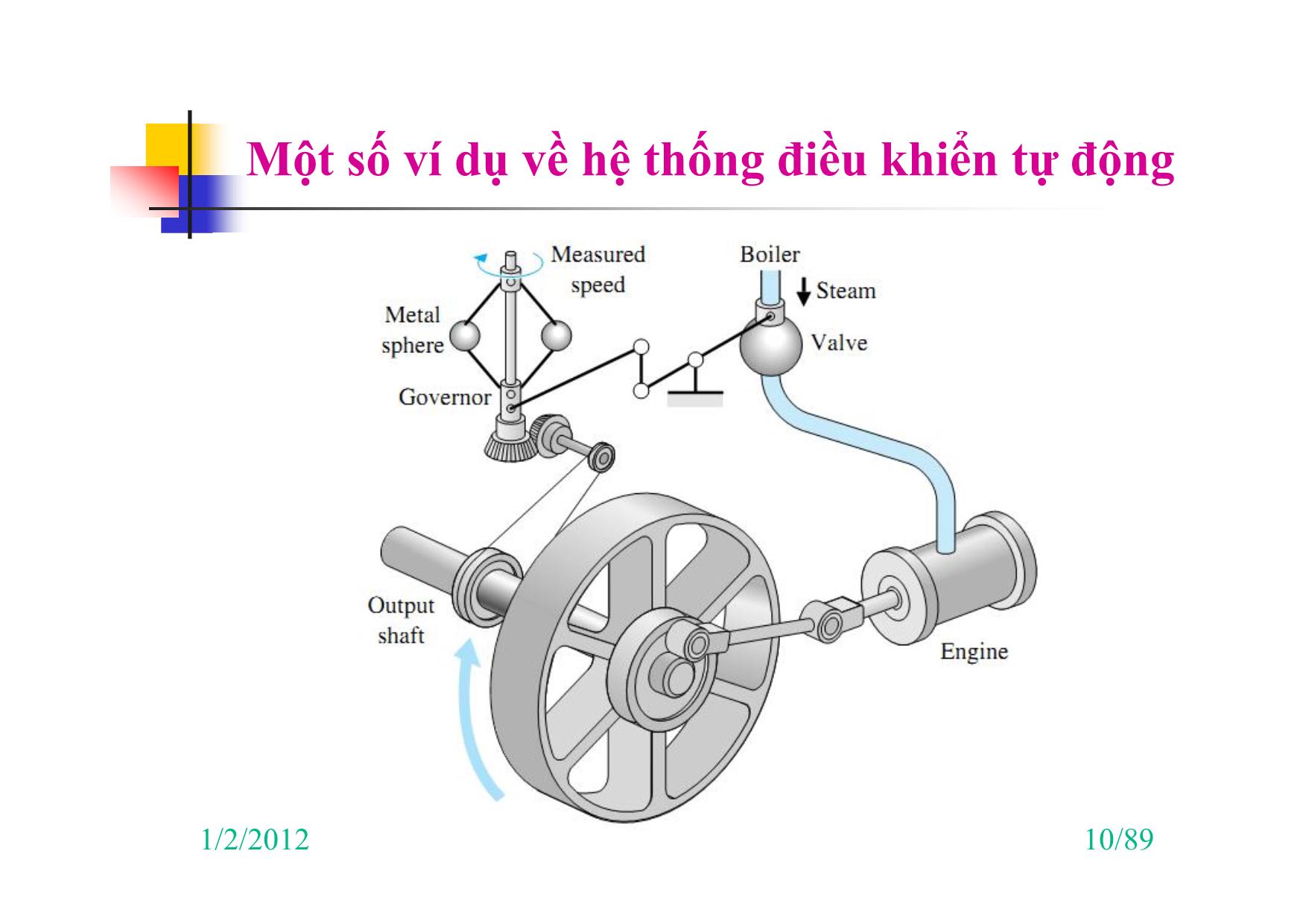
1/2/2012 10/89
Một số ví dụ về hệ thống điều khiển tự động
1/2/2012 11/89
Một số ví dụ về hệ thống điều khiển tự động
Hệ thông điều khiển không liên tục
1/2/2012 12/89
Một số ví dụ về hệ thống điều khiển tự động
1/2/2012 13/89
Một số ví dụ về hệ thống điều khiển tự động
1/2/2012 14/89
Mô hình toán học
Tại sao cần mô hình toán học để mô tả hệ thống?
 Hệ thống điều khiển thực tế đa dạng và có bản chất vật lý khác nhau.
 Cần cơ sở chung để phân tích, thiết kế.
 Với hệ thống tuyến tính hệ số hằng, có thể sử dụng phương trình vi
phân tuyến tính hệ số hằng để mô tả quan hệ giữa tín hiệu vào và tính
hiệu ra.
1 1
1 1 0 1 1 01 1
... ...
n n m m
n n m mn n m m
d y d y dy d x d x dx
a a a a y b b b b x
dt dt dt dt dt dt
- -
- -- -
+ + + + = + + + +
n: Bậc của hệ thống, hệ thống hợp thức nếu n m
ai, bi: Thông số của hệ thống
1/2/2012 15/89
Ví dụ 1:
2
2
d y t dy t
M B Ky t f t
dt dt
+ + 
M: khối lượng tác động lên bánh xe.
B: hệ số cản nhớt.
K: độ cứng lò xo 
f(t): lực do sóc: tín hiệu vào.
y(t): dịch chuyển của thân xe: tín hiệu ra 
Đặc tính động học hệ thống giảm chấn của xe 
1/2/2012 16/89
Ví dụ 2:
Đặc tính động học tốc độ xe ô tô 
dv t
M Bv t f t
dt
+ 
M: khối lượng xe, 
B: hệ số ma sát.
f(t): lực kéo của động cơ: tín hiệu vào. 
v(t): tốc độ xe: tín hiệu ra.
thông số hệ thống
1/2/2012 17/89
Ví dụ 3:
Đặc tính của mạch điện 
( ) 1( ) ( )i
di t
e Ri t L i t dt
Cdt
 + + 
 Áp dụng định luật Kirchoff ta viết
được phương trình điện áp như sau:
1 ( )oe i t dtC
Gọi ( )q i t dt , ta có phương trình vi phân dạng như sau:
1
ie Lq Rq qC
 + + 
ei: điện áp đặt vào – tín hiệu vào
q: điện tích trên tụ C – tín hiệu ra
1/2/2012 18/89
Nhận xét:
1 1
1 1 0 1 1 01 1
... ...
n n m m
n n m mn n m m
d y d y dy d x d x dx
a a a a y b b b b x
dt dt dt dt dt dt
- -
- -- -
+ + + + = + + + +
Phương trình vi phân mô tả hệ thống có dạng tổng quát như sau:
 Nhận thấy khi bậc n > 2 phương trình trên rất khó giải. Vì vậy, phân tích
hệ thống nếu chỉ dựa vào phương trình vi phân sẽ gặp rất nhiều khó khăn.
 Thiết kế hệ thống dựa vào phương trình vi phân hầu như không thực hiện
được trong trường hợp tổng quát.
Để giải quyết vấn đề này ta sử dụng 2 dạng mô tả khác, đó là:
 Hàm truyền
 Phương trình trạng thái
1/2/2012 19/89
Biến đổi Laplace:
 Định nghĩa: Biến đổi Laplace của hàm f(t) là:
( ){ } ( )
0
( ) stf t F s f t e dt
¥
-= = òL
f(t) : là hàm xác định với mọi t 0, và f(t) = 0 khi t < 0
s : là biến laplace (biến phức) và s =  + j
L : là toán tử Laplace
1/2/2012 20/89
Tính chất của phép biến đổi Laplace
 Phép biến dổi Laplace là một toán tử tuyến tính
trong đó a, b là các hằng số bất kỳ, f1(t) và f2(t) là các hàm theo thời
gian t và L là toán tử Laplace.
 Biến đổi Laplace của đạo hàm một hàm số và của tích phân một hàm số
được xác định như sau:
1/2/2012 21/89
Biến đổi Laplace của một số hàm cơ bản
 Hàm bậc thang đơn vị “hàm bậc thang, hàm step”:
 Hàm xung đơn vị “ hàm dirac (t)”: (thường dùng để mô tả nhiễu)
u(t)
1
t0
1 0
0 0
t
u t
t
( ){ }
1
u t
s
=L
1
u(t)
t0
0 0
1 0
t
t
t

 1t dt
+ 
- 
( ){ } 1td =L
1/2/2012 22/89
Biến đổi Laplace của một số hàm cơ bản
 Hàm dốc đơn vị “Ramp”:
 Hàm mũ:
a là hằng số
1
r(t)
t0 1
0
.
0 0
t t
r t t u t
t
( ){ } 2
1
r t
s
=L
1
f(t)
t0
0
.
0 0
at
at e tf t e u t
t
-
- 
( ){ }
1
f t
s a
=
+
L
1/2/2012 23/89
Biến đổi Laplace của một số hàm cơ bản
 Hàm sin:
1/2/2012 24/89
Một số biến đổi Laplace thông dụng
f(t) F(s) f(t) F(s) 
nt (n=1, 2, 3, ) 1
!
n
n
s +
 n att e- (n=1, 2, 3, ) 
( )
1
!
n
n
s a
+
+
Xung Dirac ( )td 1 ate - 
1
s a+
Đơn vị 1(t) 
1
s
 atte - 
( )
2
1
s a+
t 2
1
s
 ( )1 1 ate
a
-- 
( )
1
s s a+
( )
1
1 !
nt
n
-
-
, (n =1, 2,...n) 1
ns
 ( )
1
1 !
n
att e
n
-
-
-
, 
(n=1, 2, 3, ) 
( )
1
n
s a+
sin tw 2 2s
w
w+
 cos tw 2 2
s
s w+
( )sinate tw- 
( )
2 2s a
w
w+ +
 ( )cosate tw- 
( )
2 2
s a
s a w
+
+ +
 sinntn ne t  
- , 
21  - ,  < 1 
2
2 2
n2
n
ns s

 
 + +
 11 sinn t ne t   
-- +
-1osc  ,  < 1 
2
2 2
n( 2 )
n
ns s s

 + +
1/2/2012 25/89
Một số lưu ý
 Đạo hàm f(t): khi các điều kiện đầu triệt tiêu
 Nhân e-at vào f(t): ảnh Laplace sẽ thay s bằng (s+a) và ngược lại. Hằng
số a có thể là thực hoặc phức.
( ) ( )
n
n
n
d
f t s F s
dt±
ì üï ïï ïí ý
ï ïï ïî þ
=L
( ){ } ( )ate f t F s a- = +L
0
f(t)
t 0
g(t)
t
 Dịch trong miền thời gian: > 0.
Ảnh Laplace của g(t) bằng ảnh
Laplace của f(t) nhân với e- s:
G(s) = e- s.F(s)
1/2/2012 26/89
Một số lưu ý
 Thay đổi tỉ lệ miền thời gian:
 Đạo hàm phức F(s):
 Biến đổi Laplace của tích hai hàm f(t) và g(t):
( ).
t
f F sa a
a
ì üæ öï ïï ï÷ç ÷í ýç ÷ç ÷ï ïè øï ïî þ
=L
( ){ } ( )dtf t F s
ds
= -L
( ){ } ( )
2
2
2
d
t f t F s
ds
=L
( ){ } ( ) ( )1
nnn
n
d
t f t F s
ds
= -L
( ) ( ){ } ( ) ( )1
2
c j
c j
f t g t F p G s p dp
jp
+ ¥
- ¥
= -òL
1/2/2012 27/89
Một số lưu ý
 Giới hạn và phép biến đổi Laplace:
 Xét hàm f(t) có tồn tại f( ) hữu hạn:
 Xét hàm f(t) có F(s) và tồn tại sF(s) hữu hạn khi s :
Như vậy chúng ta có thể dự đoán được tính chất của hàm f(t) (tính được
f(0) và f( )) ngay trong miền phức thông qua F(s) mà không cần biến đổi
ngược về miền thời gian.
( ) ( )
0
lim lim
t s
f t sF s
® ¥ ®
=
( ) ( )0 lim
s
f sF s
® ¥
+ =
1/2/2012 28/89
Biến đổi Laplace ngược
 Biến đổi Laplace ngược được định nghĩa:
Với c là hằng số.
( ){ } ( ) ( )1 1
2
c j
st
c j
F s f t F s e ds
jp
+ ¥
-
- ¥
= = òL
1/2/2012 29/89
Phương pháp tìm biến đổi Laplace ngược
Bài toán: Cho F(s), thường có dạng sau:
Tìm f(t)?
Các bước tiến hành:
 B1: Phân tích F(s) thành tổng các phân thức đơn giản:
 B2: Tra bảng tìm biến đổi Laplace ngược:
( )
( )
( )
B
F s
A
s
s
=
( ) ( ) ( ) ( )n1 2F s F s F s +...+F s= +
( ){ } ( ){ } ( ){ } ( ){ }
( ) ( ) ( )1 2
1 1 1 1
n1 2
...
F s F s +...+ F s
nf t f t f t
F s- - - -
= + + +
= +L L L L
1/2/2012 30/89
Ví dụ
VD1: Mẫu số của F(s) có nghiệm đơn:
( ) 31 23 2
10 20
F s
3 58 15
aa as
s s ss s s
+
= = + +
+ ++ +
num = [10 20];
den = [1 8 15 
0];
[r, p, k] = 
residue(num, den)
r =
-3.0000
1.6667
1.3333
p =
-5
-3
0
k =
[ ]
( )1 0 1,33sa sF s == =
( ) ( )2 03 1,67sa s F s == + =
( ) ( )3 05 3sa s F s == + = -
( ) 3 51,33 1,67 3 , 0t ty t e e t- -= + - ³
1/2/2012 31/89
Ví dụ
VD2: Mẫu số của F(s) có nghiệm bội:
( )
( ) ( ) ( )
31 2
3 2 3
2
F s
11 1 1
aa as
ss s s
= = + +
++ + +
>> syms t
>> f = (2*t - t^2)*exp(-t);
>> laplace(f)
ans =
2/(s+1)^2-2/(s+1)^3
>>% simple(ans)
>> factor(ans)
ans =
2*s/(s+1)^3
>> syms s
>> F = 2*s/(s+1)^3;
>> ilaplace(F)
ans =
-(-2*t+t^2)*exp(-t)
( ) ( )
3
3
1
1 2
s
a s F s
= -
= + = -
( ) ( )
3
2
1
1 2
s
d
a s F s
ds
= -
é ù
ê ú
ê úë û
= + =
( ) ( )
2 3
1 2
1
2 1 0
s
d
a s F s
ds
= -
é ù
ê ú
ê úë û
= + =
( ) 2(2 ) , 0ty t e t t t-= - ³
1/2/2012 32/89
Ví dụ
VD3: Mẫu số của F(s) có nghiệm phức:
Tra bảng biến đổi Laplace, ta được:
( )
( )
( )
( )
( ) ( )
2 22 2
2 2 2
1 2
2 5
1 2 1 2
2 1 102 12
F s
2 5 1 2
s
s s
ss
s s s
+
= +
+ + + +
+ ++
= =
+ + + +
Matlab Symbolic:
>> syms s
>> F = (2*s+12)/(s^2+2*s+5);
>> ilaplace(F)
ans =
(2*(cos(2*t) + (5*sin(2*t))/2))/exp(t)
( ) ( ) ( )2 cos 2 5 sin 2 , 0t ty t e t e t t- -= + ³
1/2/2012 33/89
Ví dụ
VD4: Giải phương trình vi phân tuyến tính hệ số hằng:
Biến đổi Laplace 2 vế ta được:
Thay điều kiện đầu và biến đổi được:
Tra bảng biến đổi Laplace, ta được:
3 2 0 , (0) 1 (0) 2x x x x x+ +   
( ) ( ) ( ) ( ) ( ) ( )2 0 0 3 0 2 0s X s sx x sX s x X sé ù é ùê ú ê úë û ë û- - + - + =
( ) 2
5 4 3
1 23 2
s
X s
s ss s
+
= = -
+ ++ +
( ) 24 3 , 0t tx t e e t- -= - ³
1/2/2012 34/89
Hàm truyền của hệ thống điều khiển
Xét hệ thống được mô tả bởi phương trình vi phân:
Biến đổi Laplace 2 vế phương trình trên ta được:
1/2/2012 35/89
Hàm truyền của hệ thống điều khiển
Hàm truyền của hệ thống:
 Định nghĩa: Hàm truyền là tỷ số biến đổi Laplace của tín hiệu ra trên tín
hiệu vào của hệ thống khi điều kiện đầu bằng 0.
1/2/2012 36/89
Cách tìm hàm truyền
 B1: Thành lập phương trình vi phân mô tả quan hệ vào – ra của phần tử
bằng cách:
 Áp dụng các định luật Kirchoff, quan hệ dòng – áp trên điện trở, tụ
điện, cuộn cảm, ... đối với các phần tử điện.
 Áp dụng các định luật Newton, quan hệ giữa lực ma sát với vận tốc,
quan hệ giữa lực với biến dạng của lò xo, ... đối với các phần tử cơ.
 Áp dụng các định luật truyền nhiệt, định luật bảo toàn năng lượng, ...
đối với các phần tử nhiệt.
 B2: Biến đổi Laplace 2 vế phương trình vi phân được thành lập ở B1, ta
được hàm truyền cần tìm.
1/2/2012 37/89
Cách tìm hàm truyền
Hệ cơ, 
Định luật 2 
Newton
Điện,
Định luật
Kirchoff
Lò xo k, tụ điện C k  1/C x  q
Khối lượng m, 
cuộn cảm L
m  L
Cản nhớt b, điện 
trở R
b  R F  VR
Mối tương quan giữa hệ Cơ - Điện
F kx C
1
V q
C
L
di
V L
dt
dv
F m
dt
F bv RV Ri 
1/2/2012 38/89
Hàm truyền các khâu điều khiển thụ động
 Mạch tích phân bậc 1:
 Mạch vi phân bậc 1:
1/2/2012 39/89
Hàm truyền các khâu điều khiển thụ động
 Mạch sớm pha:
 Mạch trễ pha:
1/2/2012 40/89
Hàm truyền các khâu điều khiển tích cực
1/2/2012 41/89
Hàm truyền các khâu điều khiển tích cực
1/2/2012 42/89
Hàm truyền các đối tượng thường gặp
1/2/2012 43/89
Hàm truyền động cơ DC
1/2/2012 44/89
Hàm truyền động cơ DC
Iư(s)
M(s)
1/2/2012 45/89
Hàm truyền động cơ DC
1/2/2012 46/89
Hàm truyền xe ô tô
1/2/2012 47/89
Hàm truyền giảm xóc ô tô, xe máy
48/891/2/2012
Hàm truyền thang máy
1/2/2012 49/89
Hàm truyền của hệ thống tự động
1/2/2012 50/89
Hàm truyền của các hệ thống đơn giản
G1(s)
YX2
G2(s)
X1
YX1
G1G2
1/2/2012 51/89
Hàm truyền của các hệ thống đơn giản
G1
YX1
+
G2
+
YX1
G1 + G2
1/2/2012 52/89
Hàm truyền của các hệ thống đơn giản
Hệ thống hồi tiếp âm Hệ thống hồi tiếp âm đơn vị
G
YX +
-
H
G
YX +
-
YX
1
G
GH+
YX
1
G
G+
Y(s) = G(s)*[ X(s) - H(s)*Y(s)]
G s
Y s
1 G s H s
+
1/2/2012 53/89
Hàm truyền của các hệ thống đơn giản
Hệ thống hồi tiếp dương Hệ thống hồi tiếp dương đơn vị
Y(s) = G(s)*[ X(s) + H(s)*Y(s)]
G s
Y s
1 G s H s
-
G
YX +
+
H
G
YX +
+
YX
1
G
GH+-
YX
1
G
G+-
1/2/2012 54/89
Các phép biến đổi tương đương sơ đồ khối
 Chuyển bộ tổng từ phía trước ra sau một khối:
 Chuyển bộ tổng từ phía sau lên trước một khối:
G
YX1 +
±
X2
G
G
YX1 +
±
X2
G
YX1 +
±
X2
G
YX1+
±
X2
1
G
1/2/2012 55/89
Các phép biến đổi tương đương sơ đồ khối
 Chuyển điểm rẽ nhánh từ phía trước ra sau một khối:
 Chuyển điểm rẽ nhánh từ phía sau lên trước một khối:
G
YX1
X1
Y
G
X1
X1
G
1
G
G
YX1
Y
G
YX1
Y
G
1/2/2012 56/89
Các phép biến đổi tương đương sơ đồ khối
1/2/2012 57/89
Các phép biến đổi tương đương sơ đồ khối
1/2/2012 58/89
Một số chú ý
1/2/2012 59/89
Ví dụ
 VD1: Rút gọn mô hình và tìm hàm truyền hệ thống
G 2 
R + 
- 
H 2 
G 1 G 3 
H 1 
+ 
+ 
+ 
- 
Y 
YR
2 3
2 1 2 2 3 1
H G G
1 H G G 2G G H
1
- +
1/2/2012 60/89
Ví dụ
 VD2: Rút gọn mô hình và tìm hàm truyền hệ thống
1 2 3 4
3 4 2 2 3 1 1 2 3 4 31
G G G G
G G H G G H G G G G H  
1/2/2012 61/89
Một số nhận xét
 Phương pháp biến đổi sơ đồ khối là một phương pháp đơn giản.
 Khuyết điểm của PP này là không mang tính hệ thống, mỗi sơ đồ cụ thể
có thể có nhiều cách biến đổi, tùy theo trực giác người giải toán.
 Khi tính toán hàm truyền tương đương ta phải thực hiện nhiều phép tính
trên các phân thức đại số, với các hệ thống phức tạp các phép tính này
hay bị nhầm lẫn.
 Phương pháp này chỉ thích hợp để tìm hàm truyền tương đương của
các hệ thống đơn giản.
 Với các hệ thống phức tạp ta sử dụng PP hiệu quả hơn, đó là PP sơ đồ
dòng tín hiệu, sẽ được trình bầy ở mục tiếp theo.
1/2/2012 62/89
Sơ đồ dòng tín hiệu
Định nghĩa
Sơ đồ khối Sơ đồ dòng tính hiệu
 Sơ đồ dòng tín hiệu là một mạng gồm các NÚT và NHÁNH.
 NÚT: là một điểm biểu diễn một biến hay tín hiệu trong hệ thống.
 NHÁNH: là đường nối trực tiếp 2 NÚT, trên mỗi nhánh có ghi mũi tên chỉ
chiều truyền tín hiệu và có ghi hàm truyền cho biết mối quan hệ giữa tín
hiệu ở 2 NÚT
1/2/2012 63/89
Sơ đồ dòng tín hiệu
 Nút nguồn: là nút chỉ có các nhánh hướng ra.
 Nút đích: là nút chỉ có các nhánh hướng vào.
 Nút hỗn hợp: là nút có cả các nhánh ra và các nhánh vào.
 Đường tiến: là đường gồm các nhánh liên tiếp có cùng hướng tín hiệu đi
từ nút nguồn đến nút đích và chỉ qua mỗi nút một lần.
 Độ lợi của một đường tiến: là tích các hàm truyền của các nhánh trên
đường tiến đó
 Vòng kín: là đường khép kín gồm các nhánh liên tiếp có cùng hướng tín
hiệu và chỉ qua mỗi nút một lần.
 Độ lợi của một vòng kín: là tích các hàm truyền của các nhánh trên
vòng kín đó.
1/2/2012 64/89
Sơ đồ dòng tín hiệu
Đường tiến Vòng kín
Công thức Mason
 Hàm truyền tương đương từ một nút nguồn đến một nút đích của hệ
thống tự động biểu diễn bằng sơ đồ dòng tín hiệu được cho bởi:
1/2/2012 65/89
Sơ đồ dòng tín hiệu
• Pk: là độ lợi của đường tiến thứ k đi từ nút nguồn đến nút đích đang xét.
• : là định thức của graph tín hiệu, được tính bằng công thức sau:
• k: là định thức con của graph tín hiệu, k được suy ra từ bằng cách bỏ
đi các vòng kín có dính tới đường tiến Pk.
Chú ý: “không dính” = không có nút nào chung
“dính” = có ít nhất một nút chung.
1/2/2012 66/89
Thí dụ 1
 Tìm hàm truyền tương đương của hệ thống có sơ đồ dòng tín hiệu như sau:
1/2/2012 67/89
Thí dụ 1
 Định thức của sơ đồ dòng tín hiệu:
 Các định thức con:
 Hàm truyền tương đương của hệ thống:
1/2/2012 68/89
Chú ý:
 Có thể gộp hai bộ tổng liền nhau thành một nút.
 Có thể gộp một bộ tổng và một điểm rẽ nhánh liền sau bộ
tổng thành một nút.
 Không thể gộp một bộ tổng và một điểm rẽ nhánh liền
trước bộ tổng thành một nút.
1/2/2012 69/89
Thí dụ 2
 Tìm hàm truyền tương đương của hệ thống có sơ đồ khối như sau:
1/2/2012 70/89
Thí dụ 2
1/2/2012 71/89
Thí dụ 2
 Định thức của sơ đồ dòng tín hiệu:
 Các định thức con:
 Hàm truyền tương đương của hệ thống:
 Tính hàm truyền tương đương của hệ thống có sơ đồ khối sau:
1/2/2012 72/89
Thí dụ 3
1/2/2012 73/89
Thí dụ 3
1/2/2012 74/89
Thí dụ 3
 Định thức của sơ đồ dòng tín hiệu:
 Các định thức con:
 Hàm truyền tương đương của hệ thống:
1/2/2012 75/89
Phương trình trạng thái
 Trạng thái: Trạng thái của một hệ thống là tập hợp nhỏ nhất các biến (gọi
là biến trạng thái) mà nếu biết giá trị của các biến này tại thời điểm t0 và
biết các tín hiệu vào ở thời điểm t > t0, ta hoàn toàn có thể xác định được
đáp ứng của hệ thống tại mọi thời điểm t t0.
Hệ thống bậc n có n biến trạng thái. Các biến trạng thái có thể chọn là
biến vật lý hoặc không phải là biến vật lý.
 Véc tơ trạng thái: n biến trạng thái hợp thành véc tơ cột:
gọi là véc tơ trạng thái
 Bằng cách sử dụng các biến trạng thái, ta có thể chuyển phương trình vi
phân bậc n mô tả hệ thống thành hệ gồm n phương trình vi phân bậc
nhất, (gọi là hệ phương trình trạng thái)
 Trong đó:
Chú ý: Tùy theo cách đặt biến trạng thái mà một hệ thống có thể được mô tả
bằng nhiều phương trình trạng thái khác nhau.
Nếu A là ma trận thường ta gọi (*) là phương trình trạng thái ở dạng thường,
nếu A là ma trận chéo, ta gọi (*) là phương trình trạng thái ở dụng chính tắc.
1/2/2012 76/89
Phương trình trạng thái
1/2/2012 77/89
Cách thành lập phương trình trạng thái
 Thành lập phương trình trạng thái từ phương trình vi phân:
(TH: Vế phải của phương trình vi phân không chứa đạo hàm tín hiệu vào)
1/2/2012 78/89
Cách thành lập phương trình trạng thái
1/2/2012 79/89
Cách thành lập phương trình trạng thái
Thí dụ trường hợp 1
1/2/2012 80/89
Cách thành lập phương trình trạng thái
 Thành lập phương trình trạng thái từ phương trình vi phân:
(TH: Vế phải của phương trình vi phân có chứa đạo hàm tín hiệu vào)
Sinh viên về tham khảo tài liệu LT ĐKTT trang 67, 68, 69
1/2/2012 81/89
Cách thành lập phương trình trạng thái
 Thành lập phương trình trạng thái từ sơ đồ khối:
1/2/2012 82/89
Cách thành lập phương trình trạng thái
1/2/2012 83/89
Cách thành lập phương trình trạng thái
1/2/2012 84/89
Tính hàm truyền từ PTTT
1/2/2012 85/89
Các bước tìm ma trận nghịch đảo
 Bước 1: Tính định thức của ma trận A
 Nếu det(A) = 0 thì A không có ma trận nghịch đảo 
 Nếu det(A) 0 thì A có ma trận nghịch đảo , chuyển bước 2.
 Bước 2: Lập ma trận chuyển vị của A là 
 Bước 3: Lập ma trận phụ hợp của A được định nghĩa như sau
∗ = ( )nm
 là phần bù đại số của phần tử ở hàng i, cột j trong ma trận A
T
 Bước 4:  =

 ()
∗
1/2/2012 86/89
Tính hàm truyền từ PTTT
1/2/2012 87/89
Tính hàm truyền từ PTTT
1/2/2012 88/89
Nghiệm của phương trình trạng thái
1/2/2012 89/89
Quan hệ giữa các dạng mô tả toán học