Bài giảng Lý thuyết điều khiển tự động - Chương 2: Mô tả toán học phần tử và hệ thống liên tục - Nguyễn Tấn Phúc
2.1 Phương trình vi phân.
2.2 Phép biến đổi Laplace.
2.3 Hàm truyền.
2.4 Sơ đồ khối.
2.5 Hàm truyền của các khâu vật lý điển hình.
2.6 Graph tín hiệu.
2.7 Phương trình trạng thái.
Tổng quát, quan hệ giữa tín hiệu vào, tín hiệu ra của một
hệ thống liên tục tuyến tính bất biến SISO có thể mô tả bằng
phương trình vi phân tuyến tính hệ số hằng:
ai , bi : thông số của hệ thống (khối lượng, ma sát, R,L,C, )
r(t) : tín hiệu vào
y(t) : tín hiệu ra
n = bậc của hệ thống = bậc ph.trình vi phân
Với hệ thống thực tế : m n (nguyên lý nhân quả)

Trang 1

Trang 2

Trang 3

Trang 4
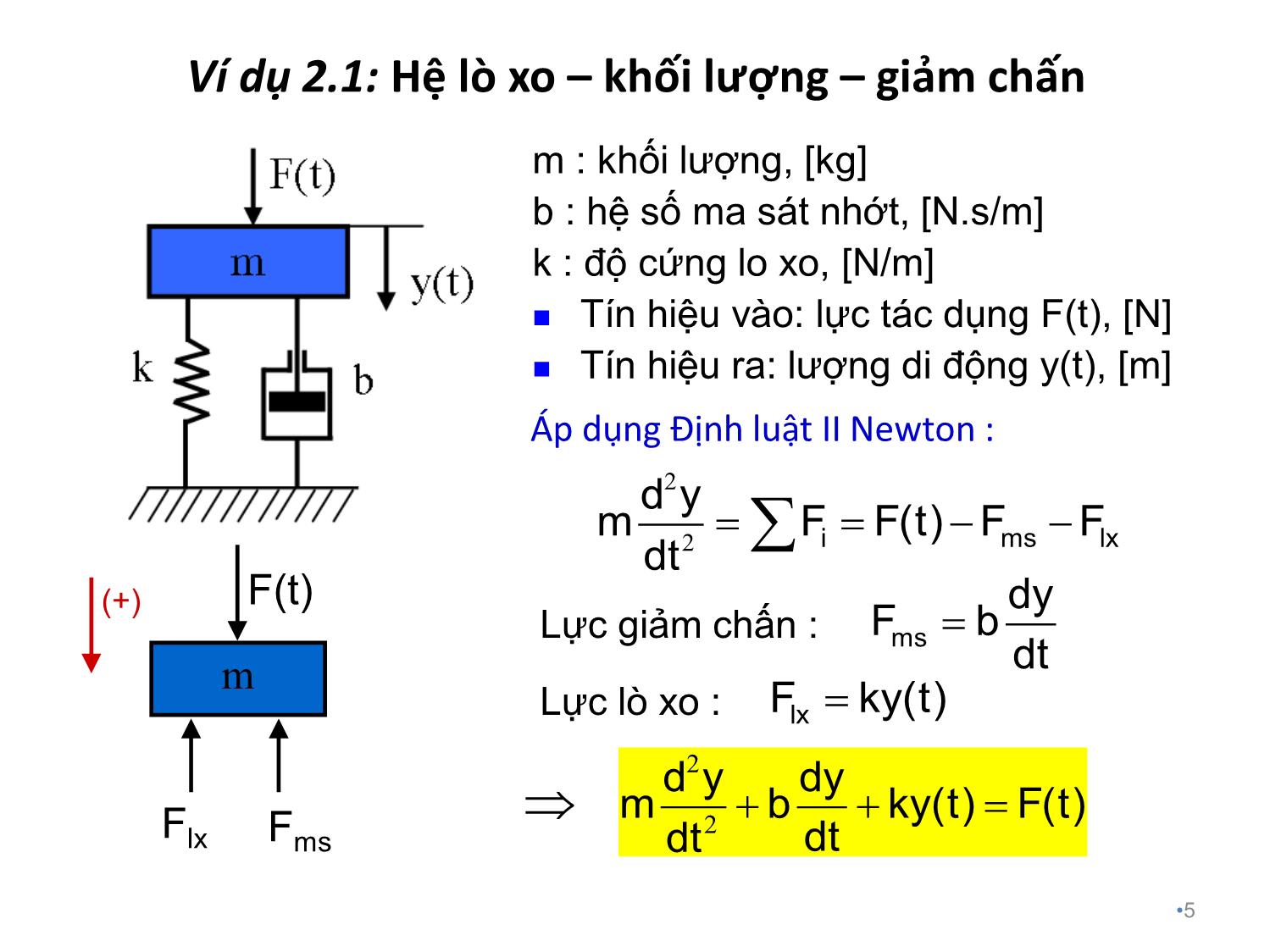
Trang 5
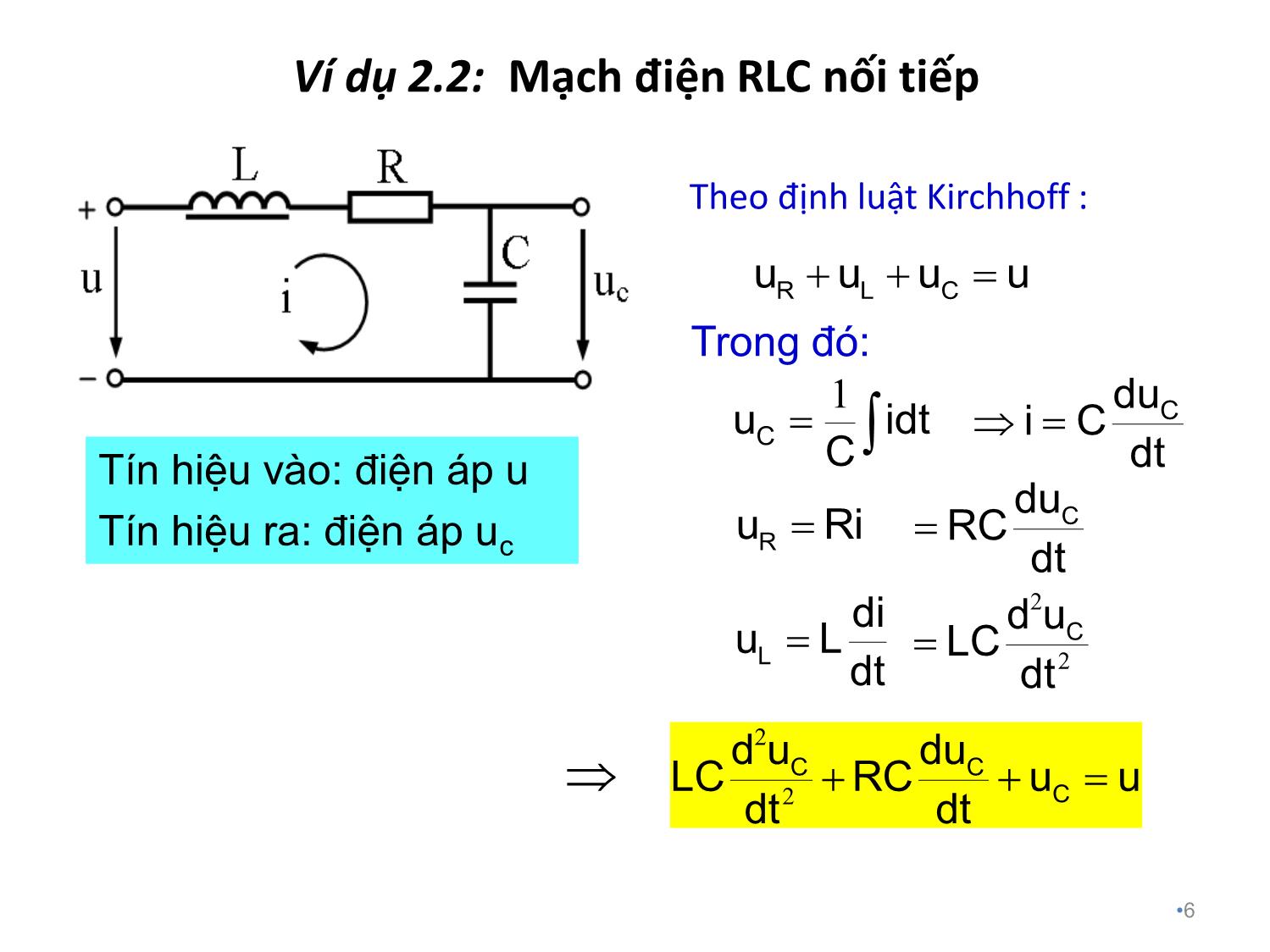
Trang 6
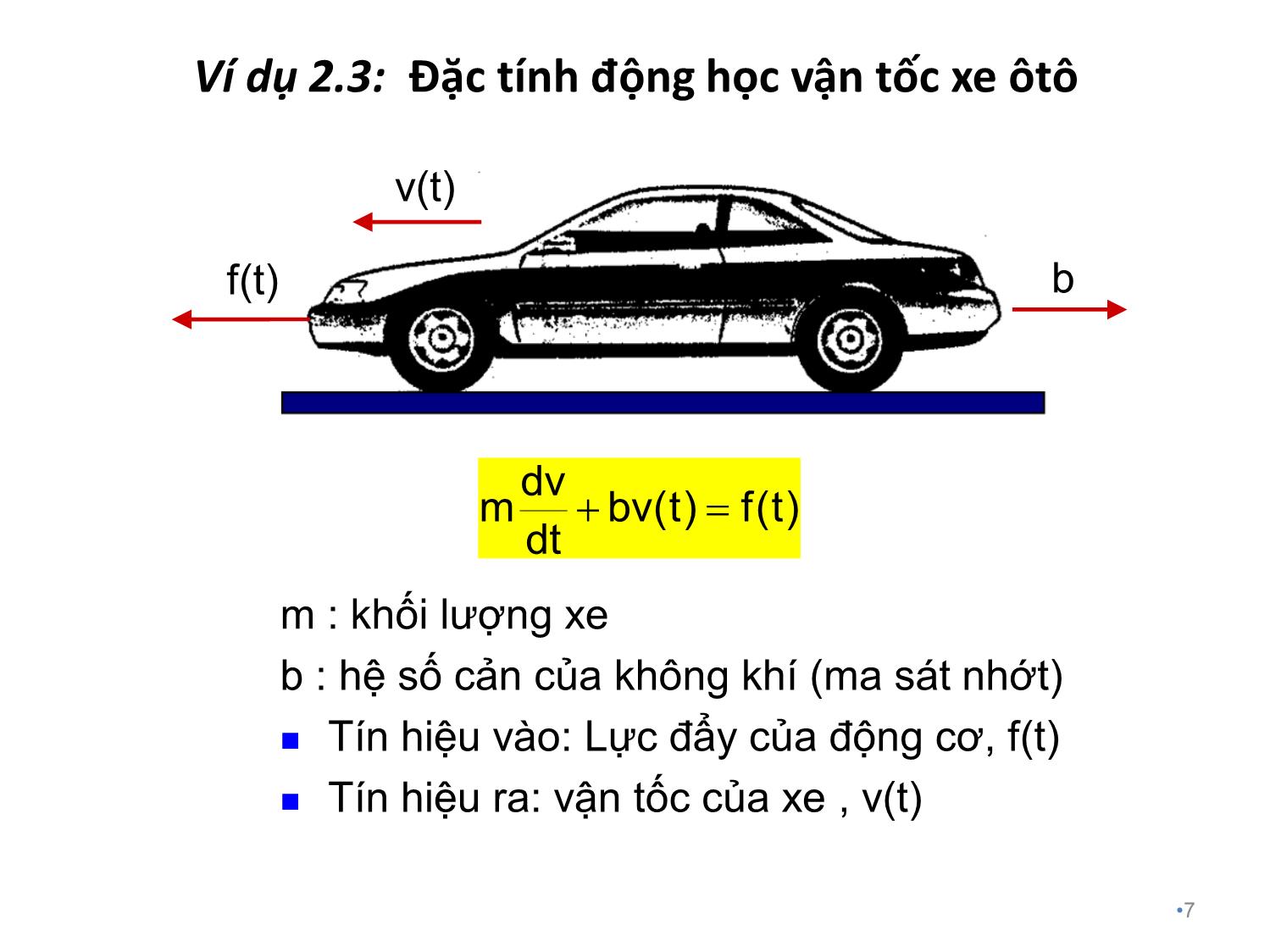
Trang 7
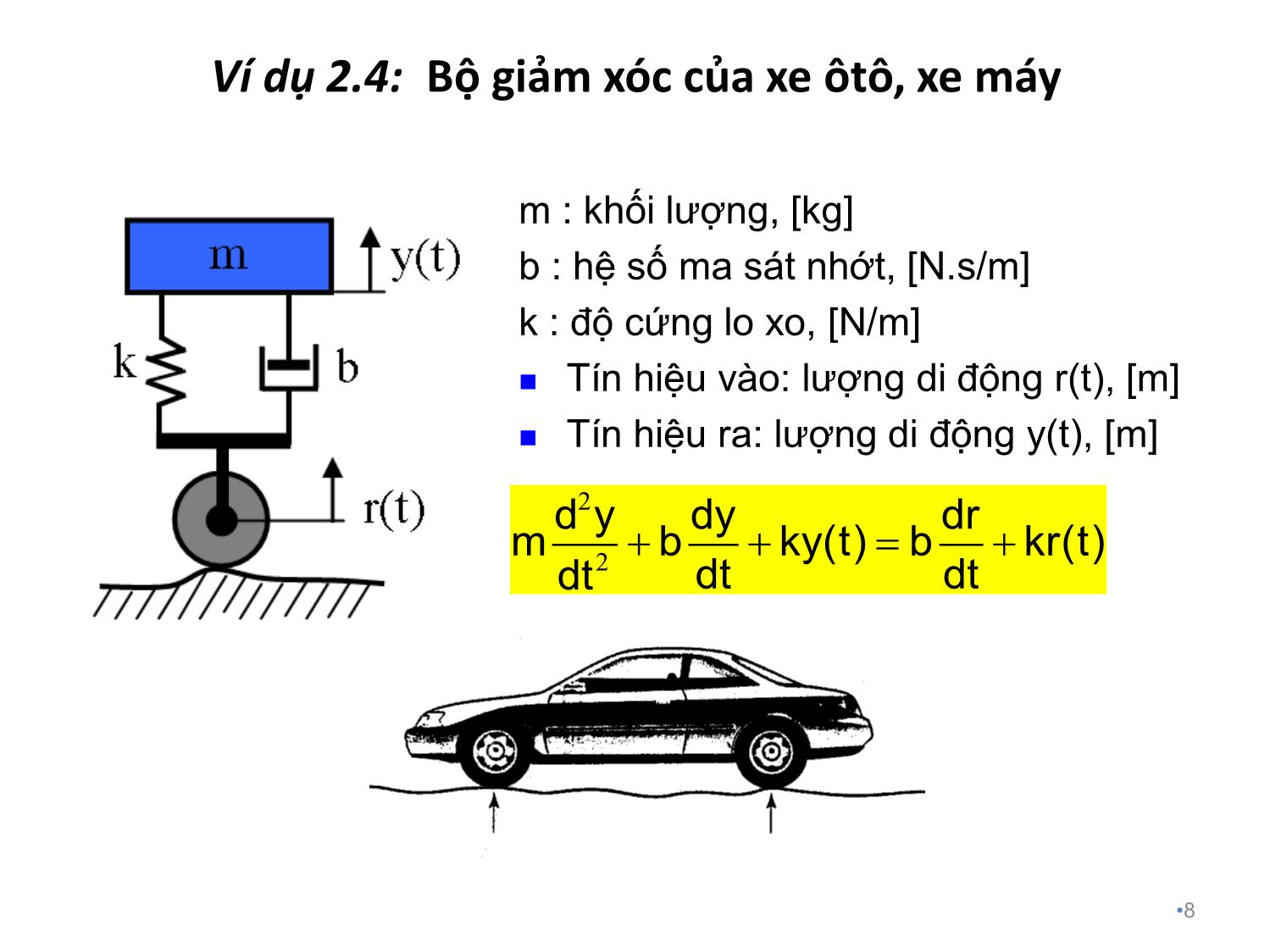
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Lý thuyết điều khiển tự động - Chương 2: Mô tả toán học phần tử và hệ thống liên tục - Nguyễn Tấn Phúc", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết điều khiển tự động - Chương 2: Mô tả toán học phần tử và hệ thống liên tục - Nguyễn Tấn Phúc

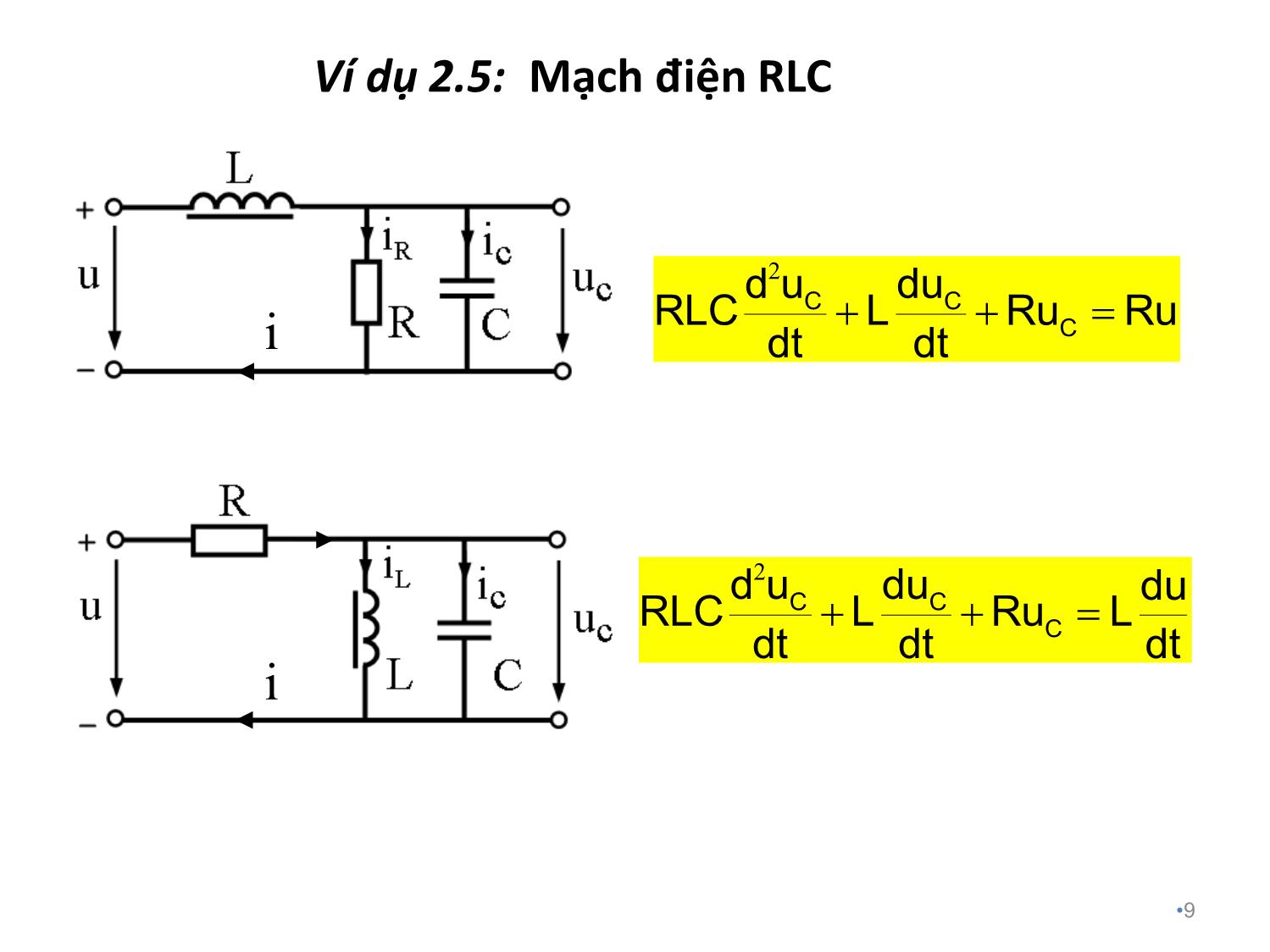
•1 TRƯỜNG ĐẠI HỌC NÔNG LÂM TPHCM. KHOA CƠ KHÍ CÔNG NGHỆ BỘ MÔN CƠ ĐiỆN TỬ. BÀI GiẢNG : LÝ THUYẾT ĐiỀU KHIỂN TỰ ĐỘNG GV: Th.S Nguyễn Tấn Phúc. phucpfiev1@gmail.com. Chương 2: Mô tả toán học Phần tử và hệ thống liên tục 2.1 Phương trình vi phân. 2.2 Phép biến đổi Laplace. 2.3 Hàm truyền. 2.4 Sơ đồ khối. 2.5 Hàm truyền của các khâu vật lý điển hình. 2.6 Graph tín hiệu. 2.7 Phương trình trạng thái. •2 •3 Chương 2: Mô tả toán học Phần tử và hệ thống liên tục 2.1 Phương trình vi phân. 2.2 Phép biến đổi Laplace. 2.3 Hàm truyền. 2.4 Sơ đồ khối. 2.5 Hàm truyền của các khâu vật lý điển hình. 2.6 Graph tín hiệu. 2.7 Phương trình trạng thái. 2.1 Phương trình vi phân •4 ai , bi : thông số của hệ thống (khối lượng, ma sát, R,L,C,) r(t) : tín hiệu vào y(t) : tín hiệu ra n = bậc của hệ thống = bậc ph.trình vi phân Với hệ thống thực tế : m n (nguyên lý nhân quả) 1 1 1 0 1 01 1 n n m m n n m mn n m m d y d y d r d r a a ... a y(t) b b ... b r(t) dt dt dt dt Tổng quát, quan hệ giữa tín hiệu vào, tín hiệu ra của một hệ thống liên tục tuyến tính bất biến SISO có thể mô tả bằng phương trình vi phân tuyến tính hệ số hằng: Ví dụ 2.1: Hệ lò xo – khối lượng – giảm chấn Áp dụng Định luật II Newton : •5 m : khối lượng, [kg] b : hệ số ma sát nhớt, [N.s/m] k : độ cứng lo xo, [N/m] Tín hiệu vào: lực tác dụng F(t), [N] Tín hiệu ra: lượng di động y(t), [m] 2 2 i ms lx d y m F F(t) F F dt 2 2 d y dy m b ky(t) F(t) dtdt ms dy F b dt lxF ky(t) Lực giảm chấn : Lực lò xo : F(t) Fms Flx m (+) Ví dụ 2.2: Mạch điện RLC nối tiếp Theo định luật Kirchhoff : •6 Tín hiệu vào: điện áp u Tín hiệu ra: điện áp uc R L Cu u u u L di u L dt 1 Cu idtC Ru Ri 2 2 C C C d u du LC RC u u dt dt Trong đó: C du i C dt C du RC dt 2 2 C d u LC dt Ví dụ 2.3: Đặc tính động học vận tốc xe ôtô •7 dv m bv(t) f(t) dt m : khối lượng xe b : hệ số cản của không khí (ma sát nhớt) Tín hiệu vào: Lực đẩy của động cơ, f(t) Tín hiệu ra: vận tốc của xe , v(t) f(t) b v(t) Ví dụ 2.4: Bộ giảm xóc của xe ôtô, xe máy •8 m : khối lượng, [kg] b : hệ số ma sát nhớt, [N.s/m] k : độ cứng lo xo, [N/m] Tín hiệu vào: lượng di động r(t), [m] Tín hiệu ra: lượng di động y(t), [m] 2 2 d y dy dr m b ky(t) b kr(t) dt dtdt •9 Ví dụ 2.5: Mạch điện RLC 2 C C C d u du RLC L Ru Ru dt dt 2 C C C d u du du RLC L Ru L dt dt dt i i Chương 2: Mô tả toán học Phần tử và hệ thống liên tục 2.1 Phương trình vi phân. 2.2 Phép biến đổi Laplace. 2.3 Hàm truyền. 2.4 Sơ đồ khối. 2.5 Hàm truyền của các khâu vật lý điển hình. 2.6 Graph tín hiệu. 2.7 Phương trình trạng thái. •10 2.2 Phép biến đổi Laplace •11 Nghieäm y(t) Nghieäm Y(s) 2.2 Phép biến đổi Laplace 2.2.1 Định nghĩa • Cho hàm thời gian f(t) xác định với mọi t 0, biến đổi Laplace của f(t) là: •12 s : biến Laplace (biến số phức) L : toán tử biến đổi Laplace F(s): biến đổi Laplce hay ảnh Laplace của f(t) Biến đổi Laplace tồn tại khi tích phân trong biểu thức định nghĩa trên là hội tụ (hữu hạn). st 0 F(s) L[f (t)] f (t)e dt 2.2 Phép biến đổi Laplace • Cho hàm phức F(s), biến đổi Laplace ngược của F(s) là một hàm thời gian f(t) xác định bởi: •13 Trong đó : C là đường cong kín được lựa chọn trong miền s j là số ảo đơn vị (j2 =-1) 1 ts c 1 f (t) L [F(s)] F(s)e ds 2 j t 0 2.2 Phép biến đổi Laplace 2.2.2 Tính chất 1) Tuyến tính 2) Ảnh của đạo hàm Giải phương trình vi phân bậc n cần n điều kiện đầu: •Bộ môn : Cơ Điện Tử •14 (n 1)f (0), f (0), f (0), ..., f (0) L [f1(t) f2(t)] = F1(s) F2(s) L[kf(t)] = kF(s) 0y( ) là vận tốc ban đầu (tại t=0). 2 điều kiện đầu: y(0) là vị trí ban đầu (tại t=0) 300 5 20 100 y(t) y(t) y(t) Ví dụ : Giải ph.trình vi phân mô tả chuyển động bậc hai: 2.2 Phép biến đổi Laplace 2a) Nếu các điều kiện đầu khác 0 •15 ( ) ( 1) 1 [ ( )] ( ) (0) n n n n i i i L f t s F s s f 2300 5 20 100s Y(s) sY(s) Y(s) R(s) 2300 5 20 100( s s )Y(s) R(s) 2L[f (t)] s F(s) sf (0) f (0) (3) 3 2L[f (t)] s F(s) s f (0) sf (0) f (0) 300 5 20 100y(t) y(t) y(t) r(t) Biến đổi Laplace 2 vế với ĐKĐ =0 ta được: Ví dụ, xét ptvp: ( )[ ( )] ( ) n nL f t s F s2b) Nếu các điều kiện đầu = 0 2.2 Phép biến đổi Laplace 3) Ảnh của tích phân •16 0 ( ) ( ) t F s L f t dt s 4) Ảnh của hàm trễ f(t-T) = f(t) khi t T = 0 khi t<T TsL[f (t T)] e F(s) 5) Ảnh của tích chập t t 1 2 1 2 1 2 0 0 f (t)*f (t) f ( ). f (t )d f (t ). f ( )d ÑN 1 2 1 2L[f (t)*f (t)] F (s).F (s) 2.2 Phép biến đổi Laplace 6) Nhân hàm f(t) với e- t •17 0 [ ( )] ( ) [ ( )] ( ) t t st L e f t e f t e dt L f t F s 8) Định lý giá trị đầu t 0 s f (0) limf (t) lim [s.F(s)] Nhân f(t) với e- t thay s bằng (s+ ) trong ảnh Laplace. 7) Định lý giá trị cuối t s 0 f ( ) lim f (t) lim [s.F ... h phân: -Tín hiệu vào: vận tốc góc (t) -Tín hiệu ra:lượng di động y(t) n_số vòng quay; P_bước ren vít t t 0 0 P y(t) P n(t)dt . (t)dt 2 P (s) K Y(s) . (s) 2 s s Y(s) K (s) s (K=P/2 : hệ số tích phân) 2.5 Hàm truyền của các khâu vật lý điển hình •Bộ môn : Cơ Điện Tử •50 Phương trình vi phân: Biến đổi Laplace 2 vế với ĐKĐ =0 : U(s) (Ls R)I(s) Hàm truyền bậc nhất: I(s) 1 G(s) U(s) Ls R 2.5.2 Phần tử điện Mạch RL nối tiếp -Tín hiệu vào: điện áp u(t) -Tín hiệu ra: dòng điện i(t) L R di u u u L Ri dt 2.5 Hàm truyền của các khâu vật lý điển hình •Bộ môn : Cơ Điện Tử •51 Phương trình vi phân: Biến đổi Laplace 2 vế với ĐKĐ =0 : 2 C(LCs RCs 1)U (s) U(s) Hàm truyền bậc hai: C 2 U (s) 1 G(s) U(s) LCs RCs 1 2.5.2 Phần tử điện Mạch RLC nối tiếp Tín hiệu vào: điện áp u(t) Tín hiệu ra: điện áp uc(t) 2 2 C C C d u du LC RC u u dt dt 2.5 Hàm truyền của các khâu vật lý điển hình •Bộ môn : Cơ Điện Tử •52 Mạch RLC nối tiếp & // i - Theo Kirchoff : C C C C du1 u i dt i C C dt L C L L C di 1 u u L i u dt dt L R L C u Ri R i i( ) 2 C RLCs Ls R U s LsU s( ) ( ) ( ) - Hàm truyền: C 2 U s Ls G s U s RLCs Ls R ( ) ( ) ( ) R Cu u u (*) - Lấy Laplace 2 vế, được: C C C du R RC u u dt u dt L -Thế vào (*) , ta được: 2 C C C d u du du RLC L Ru L dt dt dt - Lấy đạo hàm 2 vế, được: 2.5 Hàm truyền của các khâu vật lý điển hình •Bộ môn : Cơ Điện Tử •53 Khuếch đại thuật toán (op-amp) 0 2 1 1 2u K(u u ) K(u u ) - Op-amp thường được ghép nối thành các mạch khuếch đại, mạch cảm biến, bộ lọc tín hiệu, bộ điều khiển. - Tín hiệu ngõ ra u0 tỉ lệ với hiệu của hai tín hiệu vào. - Hệ số khuếch đại K 105106. 2.5 Hàm truyền của các khâu vật lý điển hình •Bộ môn : Cơ Điện Tử •54 Cảm biến Các cảm biến thường có tín hiệu ra yht(t) tỉ lệ với tín hiệu vào y(t). Ví dụ: - Một cảm biến đo áp suất trong tầm 010 bar và chuyển thành điện áp trong tầm 010V sẽ có hàm truyền là H(s)=K =10/10 = 1 [V/bar] - Một cảm biến nhiệt đo nhiệt độ trong tầm 0500C và chuyển thành điện áp trong tầm 010V sẽ có hàm truyền là H(s)=K =10/500 = 0,02 [V/C] Nếu cảm biến có độ trễ đáng kể thì được mô tả bằng hàm truyền bậc nhất. 2.5.3 Động cơ điện DC •Bộ môn : Cơ Điện Tử •55 U(s) I(s) (s) Tín hiệu vào: điện áp u Tín hiệu ra: vận tốc góc R: điện trở phần ứng L: điện cảm phần ứng Ke: hằng số sức điện động e=Ke: sức phản điện động Sử dụng 3 phương trình cơ bản: 1) Phương trình mạch điện phần ứng : e di u L Ri K dt eU(s) LsI(s) RI(s) K (s) eU(s) K (s) Ls R I(s) Biến đổi Laplace 2 vế: Sơ đồ khối (1): 1 Ls R Ke 2.5.3 Động cơ điện DC •Bộ môn : Cơ Điện Tử •56 2) Phương trình mômen điện từ: mM(t) K i(t) mM(s) K I(s) Km : hằng số mômen của động cơ I(s) M(s) Km Sơ đồ khối (2): t d M(t) J B (t) M (t) dt tM(s) Js (s) B (s) M (s) 3) Phương trình cân bằng mômen cơ: tM(s) M (s) (Js B). (s) J: mômen quán tính của đcơ và tải quy về trục động cơ B: hệ số ma sát của đcơ và tải quy về trục động cơ Mt : mômen phụ tải (nhiễu) Sơ đồ khối (3): M(s) (s) Mt(s) 1 Js B 2.5.3 Động cơ điện DC •Bộ môn : Cơ Điện Tử •57 Kết nối các SĐK (1),(2),(3) ta được SĐK chung của động cơ DC: Dùng đại số SĐK tìm hàm truyền động cơ (coi nhiễu Mt=0): Km M(s) (s) Mt(s) 1 Js B U(s) I(s) (s) Ke 1 Ls R m m m e m e K K(s) (Ls R)(Js B) G(s) K KU(s) (Ls R)(Js B) K K 1 (Ls R)(Js B) m 2 m e K(s) G(s) U(s) LJs (LB RJ)s K K RB (2-47 tr.45) 2.5.3 Động cơ điện DC •Bộ môn : Cơ Điện Tử •58 Nếu đặt : Thì hàm truyền có dạng: t L / R _là hằng số thời gian điện c J / B _là hằng số thời gian cơ m m 2 m et c m e t c t c K K / RB G(s) K KRB( s 1)( s 1) K K s ( )s 1 RB Nếu bỏ qua điện cảm: m m em m e m e K RB K K(s) K K G(s) RJU(s) RJs RB K K Ts 1 s 1 RB K K Nhận xét : Tổng quát, động cơ DC điều khiển vận tốc được mô tả bằng hàm truyền bậc hai, nếu bỏ qua điện cảm thì có thể mô tả bằng hàm truyền bậc nhất. (2-49) (2-48 tr.46) 2.5.3 Động cơ điện DC •Bộ môn : Cơ Điện Tử •59 Nếu động cơ được điều khiển góc quay (định vị); Do =d /dt (s)=s.(s) nên sơ đồ khối có thêm khâu tích phân 1/s. Hàm truyền: Nếu bỏ qua điện cảm: m m em m e m e K RB K K(s) K K G(s) U(s) s(RJs RB K K ) s(Ts 1)RJ s s 1 RB K K (2-50 tr.46) Km M(s) (s) Mt(s) 1 Js B U(s) I(s) (s) Ke 1 Ls R 1 s (s) m m e (s) K G(s) U(s) s[(Ls R)(Js B) K K ) •Bài giảng : Lý Thuyết Điều Khiển Tự Động •60 Chương 2: Mô tả toán học Phần tử và hệ thống liên tục 2.1 Phương trình vi phân. 2.2 Phép biến đổi Laplace. 2.3 Hàm truyền. 2.4 Sơ đồ khối. 2.5 Hàm truyền của các khâu vật lý điển hình. 2.6 Graph tín hiệu. 2.7 Phương trình trạng thái. •Bài giảng : Lý Thuyết Điều Khiển Tự Động Chương 2: Mô tả toán học Phần tử và hệ thống liên tục 2.1 Phương trình vi phân. 2.2 Phép biến đổi Laplace. 2.3 Hàm truyền. 2.4 Sơ đồ khối. 2.5 Hàm truyền của các khâu vật lý điển hình. 2.6 Graph tín hiệu. 2.7 Phương trình trạng thái. •61 2.7 Mô hình phương trình trạng thái •Bộ môn : Cơ Điện Tử •62 2.7.1 Giới thiệu Mô hình hàm truyền có một số điểm hạn chế: - Chỉ áp dụng được với điều kiện đầu bằng 0. - Chỉ mô tả được quan hệ tuyến tính một vào, một ra (SISO). - Chỉ áp dụng được cho hệ tuyến tính bất biến, không dùng được cho hệ phi tuyến hay hệ có thông số biến đổi theo thời gian. Để khắc phục, người ta dùng mô hình phương trình trạng thái. Trạng thái của hệ thống là tập hợp nhỏ nhất các biến (gọi là biến trạng thái) mà nếu biết giá trị các biến này tại thời điểm t=t0 và biết các tín hiệu vào ở t t0, ta hoàn toàn có thể xác định được đáp ứng của hệ thống tại mọi thời điểm t t0. Với hệ tuyến tính bất biến, thời điểm đầu thường được chọn là t0=0. Biến trạng thái không nhất thiết phải là các thông số đo được (biến vật lý). Các biến không đại diện cho các đại lượng vật lý (chỉ là biến toán học) cũng có thể chọn làm biến trạng thái. 2.7 Mô hình phương trình trạng thái •Bộ môn : Cơ Điện Tử •63 Để mô tả hệ thống bậc n cần dùng n biến trạng thái, hợp thành véctơ cột gọi là véctơ trạng thái, ký hiệu là: T 1 2 nx x x ... x Sử dụng biến trạng thái ta có thể chuyển ph. trình vi phân bậc n mô tả hệ thống thành hệ gồm n phương trình vi phân bậc nhất viết dưới dạng ma trận như sau : x(t) Ax(t) Br(t) y(t) Cx(t) Dr(t) Trong đó: x(t) là véctơ trạng thái r(t) là tín hiệu vào, y(t) là tín hiệu ra của hệ. Với hệ tuyến tính bất biến MIMO thì A, B, C, D là các ma trận hệ số. Với hệ tuyến tính bất biến SISO thì A là ma trận, B là vectơ cột, C là vectơ hàng, D là một hằng số. : Phương trình trạng thái : Phương trình ngõ ra 2.7 Mô hình phương trình trạng thái •Bộ môn : Cơ Điện Tử •64 11 12 1n 21 22 2n n1 n2 nn a a ... a a a ... a A ... ... ... ... a a ... a n 1 2 b b B b 1 2 nC c c ... c 1D d const. Nếu hệ tuyến tính bất biến SISO có hàm truyền với bậc tử số nhỏ hơn bậc mẫu số (gọi là hệ hợp thức chặt) thì D = 0. Việc chọn biến trạng thái không phải chỉ theo một cánh duy nhất. Do đó: Một hệ thống có thể mô tả bằng nhiều phương trình trạng thái khác nhau, tuỳ thuộc vào cách chọn các biến trạng thái. Ví dụ : Lập ph.trình trạng thái mô tả động cơ DC mM(t) K i(t) d M(t) J B (t) dt •Bộ môn : Cơ Điện Tử •65 3 phương trình cơ bản: -Phương trình điện : e di u L Ri K dt -Ph. trình mômen điện từ: -Phương trình cân bằng mômen cơ: (để đơn giản, xem mômen tải =0) (1) (2) (3) (1) di dt (2) và (3) d dt d J M(t) B (t) dt (4) (5) eKR 1i u L L L mK Bi J J Ví dụ : Lập ph.trình trạng thái mô tả động cơ DC e 1 1 2 KR 1 x x x u L L L m 2 1 2 K B x x x J J x Ax Bu Cx Du •Bộ môn : Cơ Điện Tử •66 e1 1 2 2m R / L K / Lx x 1/ L u x x 0K / J B / J Đặt 2 biến trạng thái 1 2x i ; x (4) và (5) 1 2 x 0 1 x e m R / L K / L A K / J B / J 1/ L B 0 C 0 1 D 0 Ví dụ 2.15 (trang 63) _Lập phương trình trạng thái •Bộ môn : Cơ Điện Tử •67 Các phương trình cân bằng lực: 2 2 1 2 2 1 2 2F b (y y ) k (y y ) m y 2 2 1 2 2 1 1 1 1 1 1 1b y y k (y y ) b y k y m y Đặt 4 biến trạng thái: 1 1 2 2 3 1 4 2x y ; x y ; x y ; x y Ta viết được hệ phương trình trạng thái : Ví dụ 2.15 (trang 63) •Bộ môn : Cơ Điện Tử •68 1 3 2 4 x x x x 2 1 2 2 3 1 1 2 1 2 3 4 1 1 1 1 k b b b1 x y (k k )x x x x m m m m 2 2 2 2 4 2 1 2 3 4 2 2 2 2 2 k k b b F(t) x y x x x x m m m m m 1 1 1 2 2 1 2 22 2 1 1 1 13 3 4 42 2 2 2 2 2 2 2 2 0 0 1 0 0 0 0 0 1x x 0 k k k b b bx x 0. .F m m m mx x 1 x xk k b b m m m m m A x B r x Ví dụ 2.15 (trang 63) x(t) Ax(t) B.F(t) y(t) Cx(t) D.F(t) •Bộ môn : Cơ Điện Tử •69 1 1 2 1 2 3 2 4 x y x x1 0 0 0 y x x0 1 0 0 x C x y Dạng tổng quát : Trong đó A, B, C được xác định như trên. Hằng số D=0. 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân x Ax Br y Cx •Bộ môn : Cơ Điện Tử •70 1) Ph.trình vi phân không chứa đạo hàm tín hiệu vào Xét hệ thống tuyến tính SISO có ph.trình vi phân: Áp dụng cách đặt biến như trên, ta sẽ tìm được phương trình trạng thái mô tả hệ thống (trường hợp này có D=0): n n 1 n 1 0 0n n 1 d y d y a ... a y(t) b r(t) dt dt (Nếu an≠ 1 ta chia hai vế cho an để đưa về dạng trên) Quy tắc đặt biến trạng thái: -Biến thứ nhất bằng tín hiệu ra: x1 =y -Biến sau bằng đạo hàm của biến trước: xi= xi-1 (i=2,..,n) 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân •Bộ môn : Cơ Điện Tử •71 2) Ph.trình vi phân có chứa đạo hàm tín hiệu vào Xét hệ thống tuyến tính SISO có ph.trình vi phân: Áp dụng cách đặt biến như trên, ta sẽ xác định được các hệ số . Từ đó lập được ph.trình trạng thái mô tả hệ thống, trong đó: n n 1 n n 1 n 1 0 n n 1 0n n 1 n n 1 d y d y d r d r a ... a y(t) b b ... b r(t) dt dt dt dt (Nếu an≠ 1 ta chia hai vế cho an để đưa về dạng trên) Quy tắc đặt biến trạng thái: - Nếu bậc vế phải = vế trái (tức bn≠0), đặt x1 =y- 0r Nếu bậc vế phải < vế trái (tức bn=0), đặt x1 =y - Đặt biến thứ i (i=2,3,,n): - Và đặt n n 1 n n 2 n 1 1 2 0 1 nx a x a x ... a x a x r 1 1i i ix x r 1 2 0[ ... ] ; T n nB D b 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân x Ax Br y Cx •Bộ môn : Cơ Điện Tử •72 Ví dụ 1: Lập phương trình trạng thái của hệ có ph.trình vi phân: Giải. Đặt hai biến trạng thái: 5y(t) 2y(t) 7y(t) r(t) 1 2 1x y ; x x 2x y Phương trình trạng thái: 1 2 2 1 2 x x 7 2 1 x x x r 5 5 5 Viết theo dạng ma trận: 1 1 2 2 x x0 1 0 .r x 7 / 5 2 / 5 x 1/ 5 1 2 x y 1 0 x 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân •Bộ môn : Cơ Điện Tử •73 Ví dụ 2: Lập phương trình trạng thái của hệ có ph.trình vi phân: Và đặt Giải. Đặt các biến trạng thái: y 5y 6y 8y 8r 24r 1 2 1 1 3 2 2 x y x x r x x r 3 2 3 1 2 0 1 3 3 2 1 3x a x a x a x r 5x 6x 8x r 1 1 2 1 2 1 3 2 1 y x y x x r y x r x r r Ta được: 3 2 1 3 2 1 3 2 1y x r r 5x 6x 8x r r r 3 2 1 3 2 1y 5y 6y 8y ( 5x 6x 8x r r r) 3 2 1 2 1 1(5x 5 r 5 r) (6x 6 r) 8x 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân •Bộ môn : Cơ Điện Tử •74 Hệ phương trình trạng thái của hệ thống là: So sánh ph.trình trên với ph.trình đã cho, ta được: Dạng ma trận: 1 2 1 3 2 1y 5y 6y 8y r ( 5 )r ( 5 6 )r 1 2 1 2 3 2 1 3 2 1 0 5 8 8 5 6 24 24 5 6 16 1 2 1 2 2 3 2 3 3 3 2 1 3 1 2 3 x x r x x x r x 8r x 5x 6x 8x r 8x 6x 5x 16r 1 1 2 2 3 3 x x 00 1 0 x 0 0 1 x 8 r 8 6 5 16x x 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân •Bộ môn : Cơ Điện Tử •75 Ví dụ 3: Lập phương trình trạng thái của hệ có ph.trình vi phân: Và đặt: Giải. Đặt các biến trạng thái như sau: y 7y 4y 2r 8r 3r 1 0 2 1 1 x y r x x r 2 1 2 0 1 2 2 1 2x a x a x r 7x 4x r 1 0 1 0 2 1 0 2 1 0 2 1 2 1 07x 4x r r r y x r y x r x r r y x r r Ta được: 2 1 2 1 0y 7y 4y ( 7x 4x r r r) 2 1 0 1 0(7x 7 r 7 r) (4x 4 r) Đáp ứng ngõ ra: 1 1 2 3 x y x 1 0 0 x x 2.7.2 Lập ph.trình trạng thái từ ph.trình vi phân •Bộ môn : Cơ Điện Tử •76 Hệ phương trình trạng thái của hệ thống là: Dạng ma trận: 0 1 0 1 2 1 0 2 1 0 2 7 8 6 7 4 3 3 7 4 37 1 1 0 2 2 2 1 2 1 2 x x r x 2 x 7x 4x r 4x 7x 37r 1 1 2 2 x x0 1 6 r 4 7x x 37 1 2 x y 0 1 2r x So sánh ph.trình trên với ph.trình đã cho, ta được: 0 1 0 2 1 0y 7y 4y r ( 7 )r ( 7 4 )r 2.7.3 Lập ph.trình trạng thái từ hàm truyền, sơ đồ khối y 5y 6y 8y 8r 24r •Bộ môn : Cơ Điện Tử •77 Cách 1: Hàm truyền ph.trình vi phân ph.trình trạng thái (Xem cách giải ví dụ 2.19 trang 69 sách ĐKTĐ ) Ví dụ: Cách 2: Đặt biến trạng thái trực tiếp trên sơ đồ khối Ví dụ: 3 2 Y(s) 8s 24 G(s) R(s) s 5s 6s 8 3 2(s 5s 6s 8).Y(s) (8s 24).R(s) (tiếp tục giải như ở ví dụ 2 mục 2.7.2 ) Lấy Laplace ngược 2 vế 2.7.4 Tìm hàm truyền từ phương trình trạng thái •Bộ môn : Cơ Điện Tử •78 Xét hệ thống tuyến tính SISO có ph.trình trạng thái: - Để tránh phải tính ma trận nghịch đảo, có thể dùng công thức: x Ax Br y Cx Dr Hệ thống sẽ có hàm truyền: 1Y(s)G(s) C(sI A) B D R(s) 1 det(sI A BC)G(s) C(sI A) B D 1 D det(sI A) - Phương trình đặc tính của hệ thống: det(sI A) 0 (xem chứng minh tr. 71_sách ĐKTĐ) 2.7.4 Tìm hàm truyền từ phương trình trạng thái •Bộ môn : Cơ Điện Tử •79 Ví dụ 2.21 (trang 71) Xét hệ thống có ph.trình trạng thái: 1G(s) C(sI A) B D Cách 1: Hàm truyền 1 1 2 2 x (t) x5 1 2 r(t) x (t) x1 0 0 1 2 x (t) y(t) 1 0,5 x (t) 1 0 5 1 s 5 1 (sI A) s 0 1 1 0 1 s 1 1 a b d b1 M c d c adet(M) 1 2 s 1 s 11 1 (sI A) 1 s 5 1 s 5det(sI A) s 5s 1 Hàm truyền của hệ thống =? 2.7.4 Tìm hàm truyền từ phương trình trạng thái •Bộ môn : Cơ Điện Tử •80 1 2 s 1 s 11 1 (sI A) 1 s 5 1 s 5det(sI A) s 5s 1 1 2 2 s 1 2 2s1 1 (sI A) B 1 s 5 0 2s 5s 1 s 5s 1 1 2 2 2s1 2s 1 C(sI A) B 1 0,5 2s 5s 1 s 5s 1 1 2 2s 1 G(s) C(sI A) B D s 5s 1 2.7.4 Tìm hàm truyền từ phương trình trạng thái •Bộ môn : Cơ Điện Tử •81 1 0 5 1 s 5 1 sI A s 0 1 1 0 1 s s 5 1 2 sI A BC 1 0,5 1 s 0 1 det(sI A BC)G(s) C(sI A) B 1 det(sI A) 2 2 2 s 7s 2 2s 1 G(s) 1 s 5s 1 s 5s 1 Cách 2: Hàm truyền s 5 1 2 1 s 7 2 1 s 0 0 1 s Tổng kết chương 2 •Bộ môn : Cơ Điện Tử •82 Một hệ thống có thể mô tả bằng một trong ba dạng mô hình: Ph.trình vi phân, hàm truyền và ph.trình trạng thái. Ba dạng mô hình này có thể chuyển đổi qua lại. Ph.trình vi phân Hàm truyền Ph.trình trạng thái L-1 L Đặt x 1( ) ( ) G s C sI A B D
File đính kèm:
 bai_giang_ly_thuyet_dieu_khien_tu_dong_chuong_2_mo_ta_toan_h.pdf
bai_giang_ly_thuyet_dieu_khien_tu_dong_chuong_2_mo_ta_toan_h.pdf

