Bài giảng Lý thuyết điều khiển tự động - Bài 6: Đặc tính thời gian của hệ thống bậc hai - Đỗ Tú Anh
Phân tích hệ thống trong miền thời gian
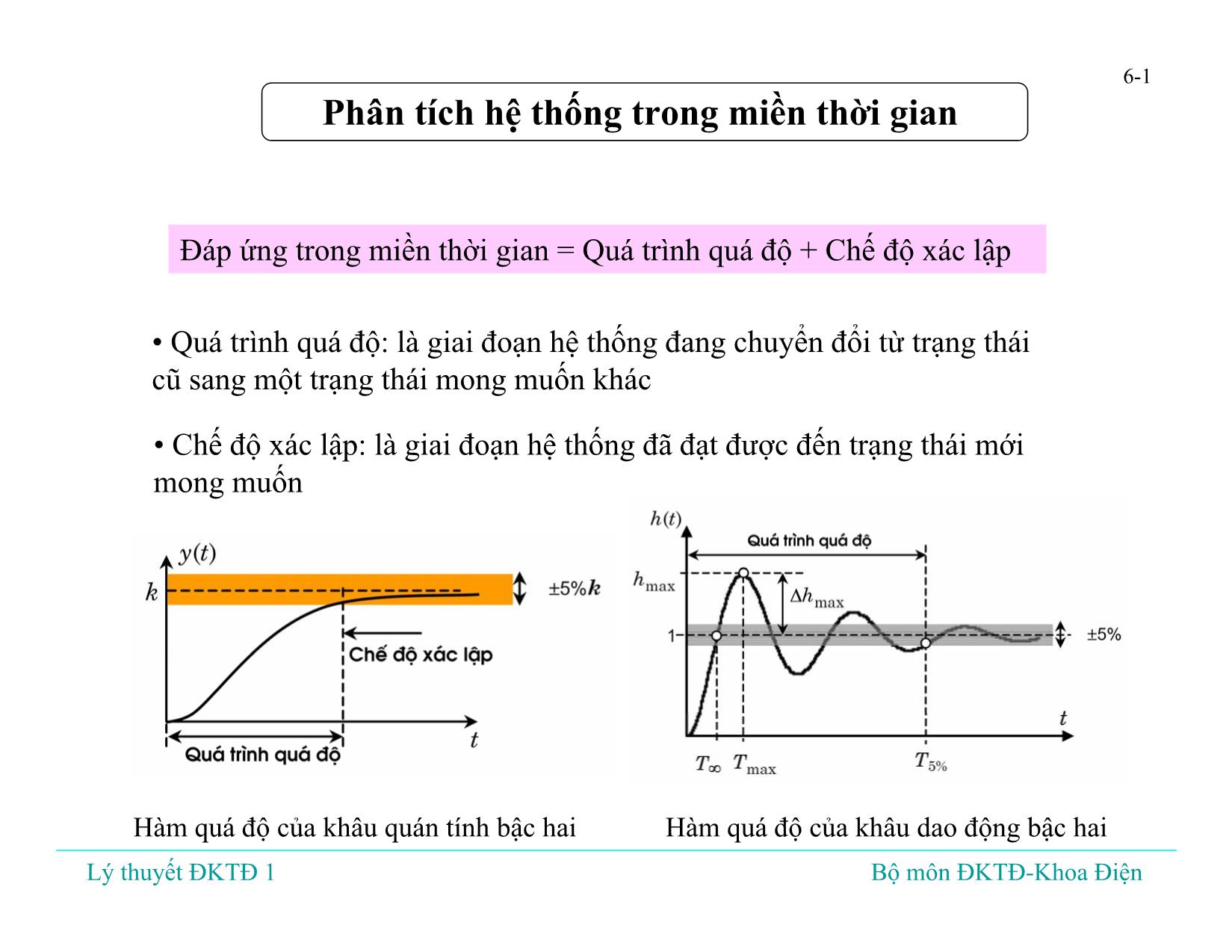
Đáp ứng trong miền thời gian = Quá trình quá độ + Chế độ xác lập
• Quá trình quá độ: là giai đoạn hệ thống đang chuyển đổi từ trạng thái
cũ sang một trạng thái mong muốn khác
• Chế độ xác lập: là giai đoạn hệ thống đã đạt được đến trạng thái mới
mong muốn
Đáp ứng cơ sở
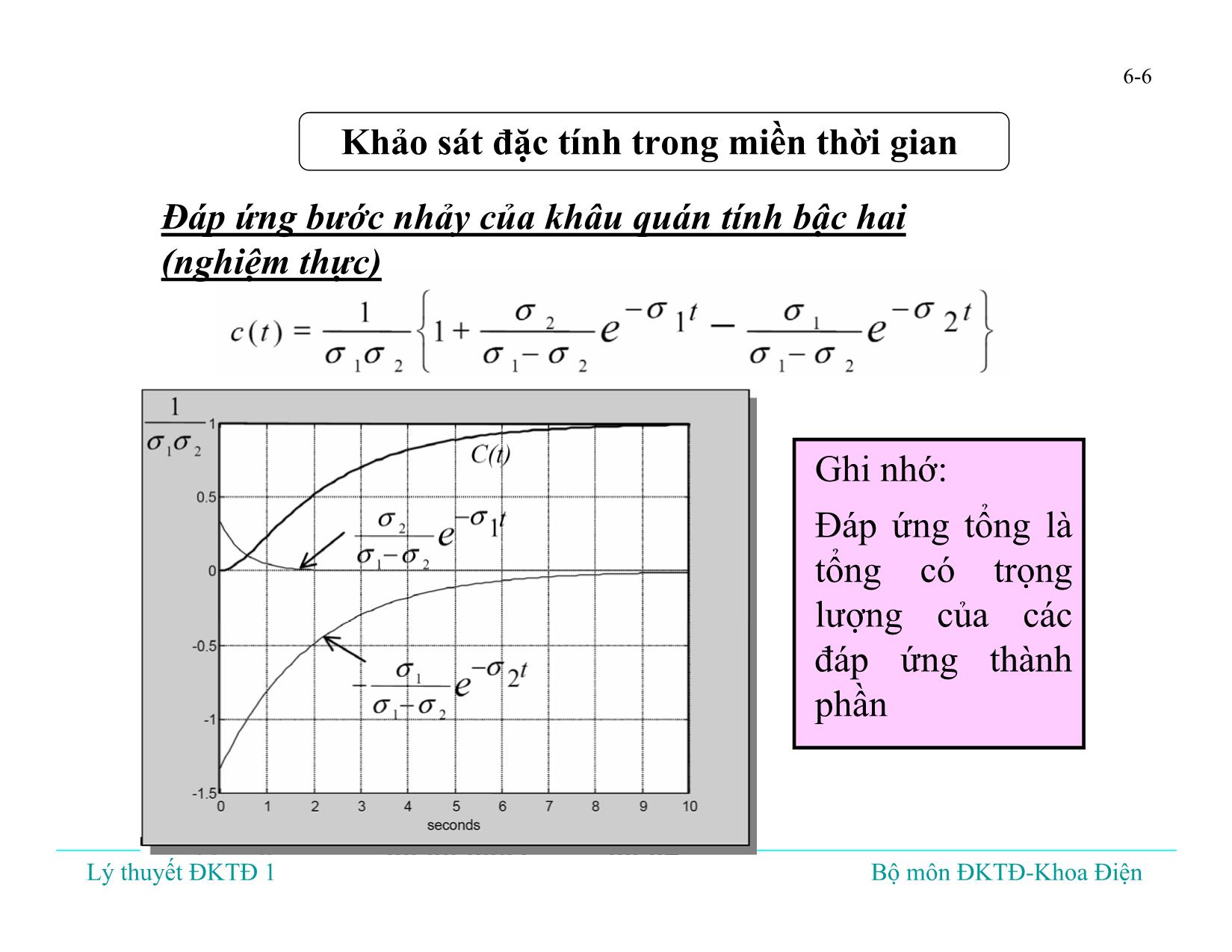
• Đáp ứng tổng được tạo thành từ tổng của các đáp ứng hàm
mũ thành phần và một tín hiệu hằng. Các đáp ứng này đgl
đáp ứng cơ sở, hay các chế độ (mode) của hệ thống,
1t
e
−σ và e−σ 2t .
• Các đáp ứng này sẽ suy giảm 37% của giá trị ban đầu của
chúng khi ở chế độ thứ nhất và khi ở chế độ
thứ hai. Các thời gian này tương ứng với các hằng số thời
gian ở các chế độ.
t =1 σ1 t =1 σ 2
τ1 1 =1 σ và τ 2 2 =1 .
Trang 1
Trang 2

Trang 3

Trang 4

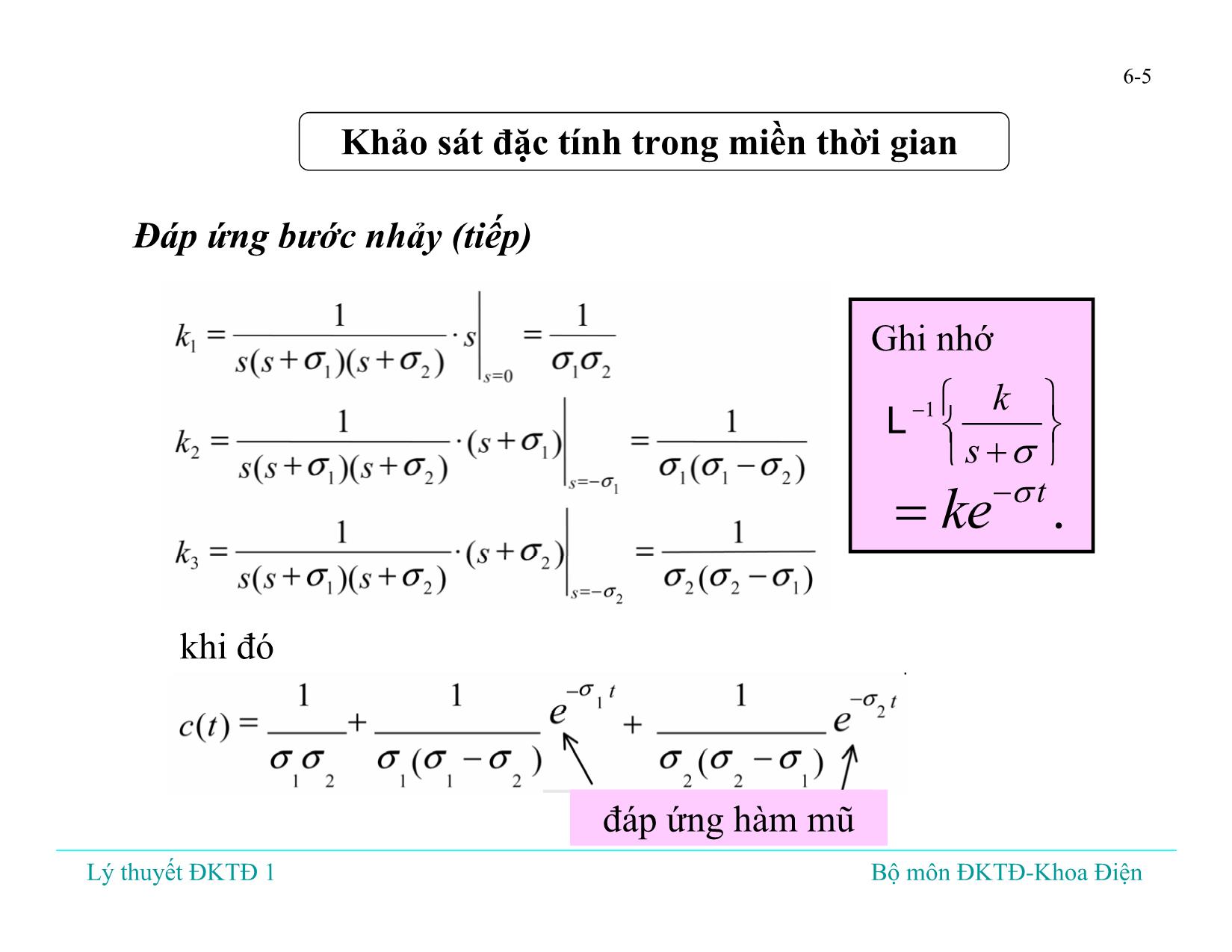
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết điều khiển tự động - Bài 6: Đặc tính thời gian của hệ thống bậc hai - Đỗ Tú Anh
Lý thuyết Điều khiển tự động 1 ThS. Đỗ Tú Anh Bộ môn Điều khiển tự động Khoa Điện, Trường ĐHBK HN Đặc tính thời gian của hệ thống bậc hai Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Phân tích hệ thống trong miền thời gian Đáp ứng trong miền thời gian = Quá trình quá độ + Chế độ xác lập • Quá trình quá độ: là giai đoạn hệ thống đang chuyển đổi từ trạng thái cũ sang một trạng thái mong muốn khác • Chế độ xác lập: là giai đoạn hệ thống đã đạt được đến trạng thái mới mong muốn Hàm quá độ của khâu quán tính bậc hai Hàm quá độ của khâu dao động bậc hai 6-1 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Các khâu bậc hai • Xét lời giải tổng quát cho khâu bậc hai sau đây Sử dụng biến đổi Laplace để giải phương trình 6-2 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Đáp ứng bước nhảy – Trường hợp nghiệm thực • Giả thiết với 0, ( ) 0t r t< = và (0) (0) 0,c dc dt= = thì • Với tín hiệu vào bước nhảy, ( ) 1R s s= 6-3 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Đáp ứng bước nhảy (tiếp) • Giả sử phương trình đặc tính có hai nghiệm thực. • Sử dụng phép phân tích C(s) thành tổng các hàm phân thức tối giản để tìm ảnh Laplace ngược. trong đó các hệ số 1 2 3, ,k k k được tính toán như sau: 6-4 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Đáp ứng bước nhảy (tiếp) khi đó đáp ứng hàm mũ Ghi nhớ 1 k s σ − ⎧ ⎫⎨ ⎬+⎩ ⎭L .tke σ−= 6-5 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Ghi nhớ: Đáp ứng tổng là tổng có trọng lượng của các đáp ứng thành phần Đáp ứng bước nhảy của khâu quán tính bậc hai (nghiệm thực) 6-6 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Đáp ứng cơ sở • Đáp ứng tổng được tạo thành từ tổng của các đáp ứng hàm mũ thành phần và một tín hiệu hằng. Các đáp ứng này đgl đáp ứng cơ sở, hay các chế độ (mode) của hệ thống, 1te σ− và 2 .te σ− • Các đáp ứng này sẽ suy giảm 37% của giá trị ban đầu của chúng khi ở chế độ thứ nhất và khi ở chế độ thứ hai. Các thời gian này tương ứng với các hằng số thời gian ở các chế độ. 11t σ= 21t σ= 1 11τ σ= 2 21 .τ σ=và 6-7 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Đáp ứng cơ sở • Điều gì sẽ xảy ra nếu có một nghiệm là số thực dương? • Yếu tố nào sẽ ảnh hưởng đến tốc độ đáp ứng của hệ thống? • Ghi nhớ rằng, phương trình đặc tính được định nghĩa từ đa thức mẫu số của hàm truyền đạt, và là các nghiệm của phương trình đặc tính này. 1 2,σ σ Câu hỏ i 6-8 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Đáp ứng bước nhảy – Trường hợp nghiệm phức • Giả sử phương trình đặc tính có hai nghiệm phức: • Sử dụng phép phân tích C(s) thành tổng các hàm phân thức tối giản để tìm ảnh Laplace ngược. trong đó các hệ số 1 2 3, ,k k k được tính toán như sau: 2 2 . 2 4 a as as b s j b jσ ω+ + ⇒ = − ± − = − ± 6-9 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Đáp ứng bước nhảy (tiếp) Khảo sát đặc tính trong miền thời gian trong đó arctg .ωθ σ= Khi này đáp ứng thời gian sẽ nhận được bằng cách sử dụng phép biến đổi Laplace ngược như sau. 6-10 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian tắt dần theo hàm mũ Đây là đáp ứng dạng hình sin tắt dần. Đáp ứng bước nhảy của khâu dao động bậc hai (nghiệm phức) 6-11 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát đặc tính trong miền thời gian Đáp ứng bước nhảy của khâu dao động bậc hai (nghiệm phức) Dạng sóng sin với tần số ω và tắt dần theo hàm e-st. 6-12 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Tần số riêng và hệ số tắt dần • Khi ta có hệ không tắt dần với tần số nhận được đgl tần số riêng • Tỉ số giữa hằng số tắt dần với tần số riêng đgl hệ số tắt dần • Mối quan hệ giữa hằng số tắt dần với hệ số tắt dần, giữa tần số tắt dần và tần số riêng là 0a = .n bω = σ . n σς ω= ,nσ ςω= 21 .nω ω ς= − Khâu dao động bậc hai 2 2 . 2 4 a as as b s j b jσ ω+ + ⇒ = − ± − = − ± 6-13 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Tần số riêng và hệ số tắt dần • Dạng chuẩn của khâu bậc hai dưới dạng biểu thức của và ς nω • Đáp ứng bước nhảy dưới dạng biểu thức của vàς nω trong đó 21- arctg . ςθ ς ⎛ ⎞⎜ ⎟= ⎜ ⎟⎝ ⎠ Khâu dao động bậc hai 6-14 Khâu dao động bậc hai Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Đáp ứng bước nhảy 6-15 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Các khâu bậc hai Biểu diễn các điểm cực trên mặt phẳng phức “s-plane” • Nghiệm của ptđt, cũng chính là điểm cực của hệ có thể được biểu diễn và giải thích trên mp phức • Xét cặp nghiệm phức liên hợp sau: 1 1s jσ ω= − ± với 2 21 1 1nω ω σ= + và 1 2 2 1 1 .σς ω σ= + Hệ số tắt dần có quan hệ với góc θ như sau Tần số riêng chính bằng khoảng cách từ tâm đến các điểm cực 1 12 2 1 1 cos( ) .σθ ςω σ= =+ 6-16 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Các khâu bậc hai Biểu diễn nghiệm trên mặt phẳng phức “s-plane” Hệ số tắt dần có quan hệ với góc θ như sau Tần số riêng chính bằng khoảng cách từ tâm đến các điểm cực 6-17 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Các khâu bậc hai Ảnh hưởng của vị trí các điểm cực trên mặt phẳng phức • Rời điểm cực sang bên phải hệ số tắt dần giảm, tần số tiến đến tần số riêng. • Rời điểm cực ra xa trục thực hệ số tắt dần giảm, tần số tăng. • Rời điểm cực dọc theo đường thẳng với góc θ không đổi hệ số tắt dần không đổi, tần số riêng tăng. • Rời điểm cực cho nằm trên trục ảo dao động điều hòa, hệ số tắt dần bằng 0. • Rời điểm cực sang bên phải trục ảo dao động tăng dần, hệ mất ổn định. ⇒ ⇒ ⇒ ⇒ ⇒ 6-18 Ảnh hưởng của vị trí các điểm cực trên mặt phẳng phức Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Các khâu bậc hai 6-19 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát chất lượng hệ thống bậc hai • Tính ổn định Xác định hệ số tắt dần hoặc miền thuộc mp phức ứng với hệ số tắt dần nhỏ nhất. Xác định độ quá điều chỉnh (percentage overshoot-P.O.) lớn nhất cho các hệ bậc hai 6-20 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Khảo sát chất lượng hệ thống bậc hai • Tốc độ đáp ứng Xác định thời gian tăng (rise time), Tr (khoảng tg từ 10% đến 90% của giá trị xác lập) cho các hệ bậc hai Xác định thời gian đạt tới đỉnh đầu tiên Tp 6-21 Khảo sát chất lượng hệ thống bậc hai • Kết hợp tính ổn định và tốc độ đáp ứng Xác định giá trị lớn nhất của phần thực của các nghiệm. Các nghiệm sẽ nằm bên trái của giá trị giới hạn Xác định thời gian xác lập, Ts (thời gian nằm lại trong phạm vi so với giá trị xác lập) δ± Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Với thì 6-22
File đính kèm:
 bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_6_dac_tinh_thoi_g.pdf
bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_6_dac_tinh_thoi_g.pdf

