Bài giảng Lý thuyết điều khiển tự động - Bài 3: Mô hình toán học của hệ liên tục tuyến tín - Đỗ Tú Anh

Lý thuyết Điều khiển tự động 1
ThS. Đỗ Tú Anh
Bộ môn Điều khiển tự động
Khoa Điện, Trường ĐHBK HN
Mô hình toán
học của hệ liên
tục tuyến tính
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Các dạng mô hình liên tục tuyến tính
Phương trình vi phân (hệ SISO)
1 1
1 1 0 1 1 01 1
n n m m
n n m mn n m m
d y d y dy d u d u dua a a a y b b b b u
dt dt dt dt dt dt
− −
− −− −+ + + + = + + + +" "
bậc của mô hình
Cho biết sâu sắc bản chất của các mối liên kết và tương tác, rất khó sử
dụng cho phân tích và thiết kế hệ thống, đặc biệt là với MH bậc cao.
⇒
Hàm truyền đạt (hệ SISO)
Được định nghĩa là tỷ số giữa ảnh Laplace của tín hiệu ra và ảnh Laplace 
của tín hiệu vào G(s)=Y(s)/U(s) với toàn bộ sơ kiện bằng 0.
1
1 0
1
1 1 0
( )
m m
m
n n
n n
b s b s b s bG s
a s a s a s a
−
−
−
+ + + += + + + +
"
"
m n≤ hàm hợp thức
m n< hàm hợp thức chặt
3-1
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Phương trình vi phân và hàm truyền đạt
Ví
dụ
Hàm truyền, G(s)
Cơ hệ lò xo-vật
Ghi nhớ
• Đa thức mẫu số đgl đa thức đặc tính
• Nghiệm của đa thức tử số đgl điểm không của hệ thống
• Nghiệm của đa thức mẫu số đgl điểm cực của hệ thống
3-2
Lực ma sát
Lực cản của lò xo
Lực gây ra gia tốc của vật
Biến đổi Laplace
Do đó
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Các dạng mô hình liên tục tuyến tính (tiếp)
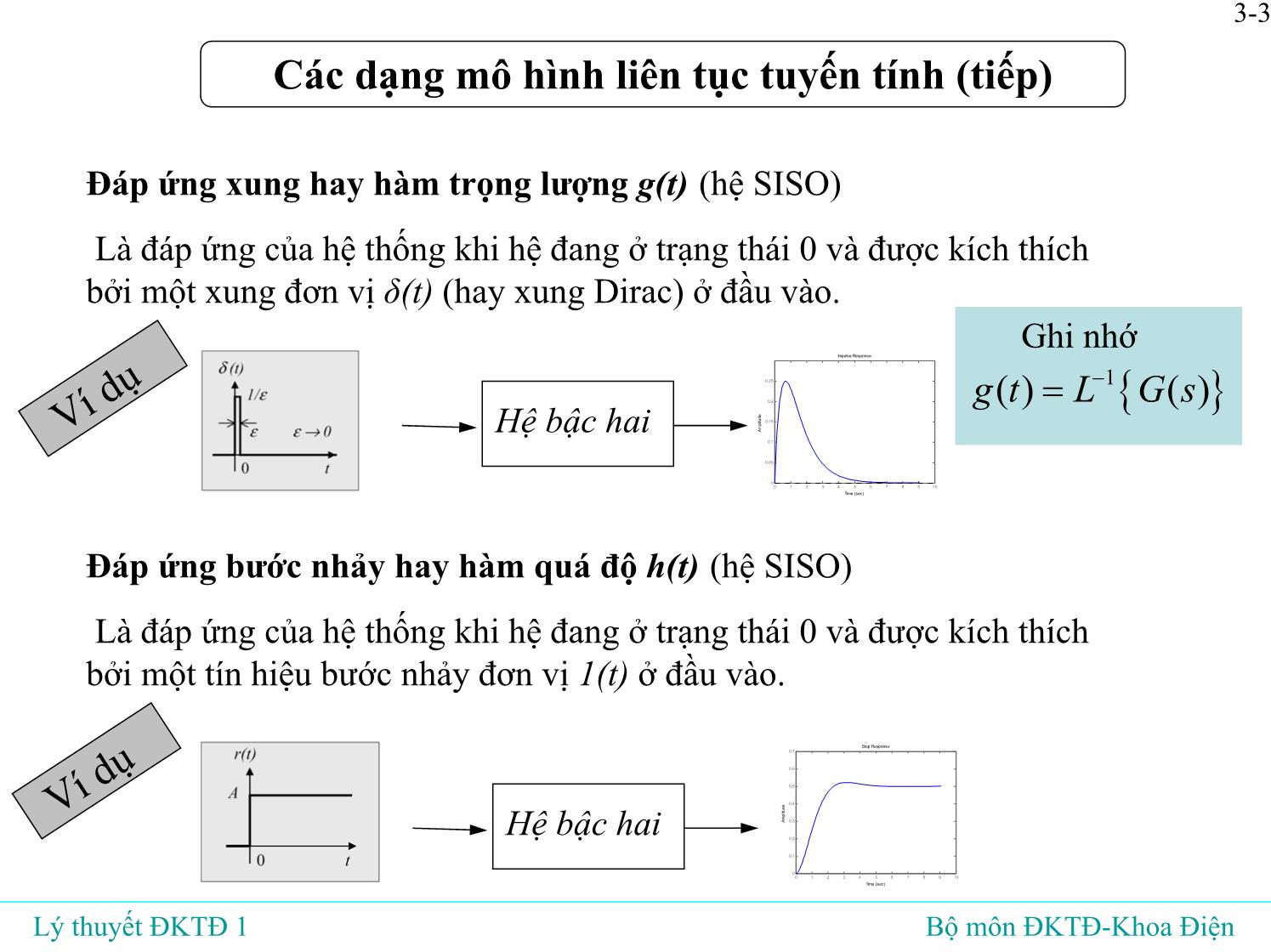
Đáp ứng xung hay hàm trọng lượng g(t) (hệ SISO)
Là đáp ứng của hệ thống khi hệ đang ở trạng thái 0 và được kích thích
bởi một xung đơn vị δ(t) (hay xung Dirac) ở đầu vào.
Đáp ứng bước nhảy hay hàm quá độ h(t) (hệ SISO)
Là đáp ứng của hệ thống khi hệ đang ở trạng thái 0 và được kích thích
bởi một tín hiệu bước nhảy đơn vị 1(t) ở đầu vào.
{ }1( ) ( )g t L G s−=
Ghi nhớ
Hệ bậc hai
Step Response
Time (sec)
A
m
p
l
i
t
u
d
e
0 1 2 3 4 5 6 7 8 9 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Ví
dụ
0 1 2 3 4 5 6 7 8 9 10
0
0.05
0.1
0.15
0.2
0.25
Impulse Response
Time (sec)
A
m
p
l
i
t
u
d
eHệ bậc haiVí
dụ
3-3
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Các dạng mô hình liên tục tuyến tính (tiếp)
Mô hình trạng thái (cả hệ SISO và MIMO)
• Khái niệm “trạng thái”: Trạng thái của một HT là một tập hợp các biến (đgl
biến trạng thái) mà tại thời điểm ban đầu t0 nào đó, cùng với các biến đầu
vào, có thể xác định được hoạt động của HT trong khoảng thời gian 0.t t≥
• Xét hệ gồm m-đầu vào, p-đầu ra, n-biến trạng thái 
3-4
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Mô hình trạng thái (tiếp)
 có quan hệ giữa các biến đầu vào và các biến trạng thái như sau
Đặt
⇒
3-5
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Mô hình trạng thái (tiếp)
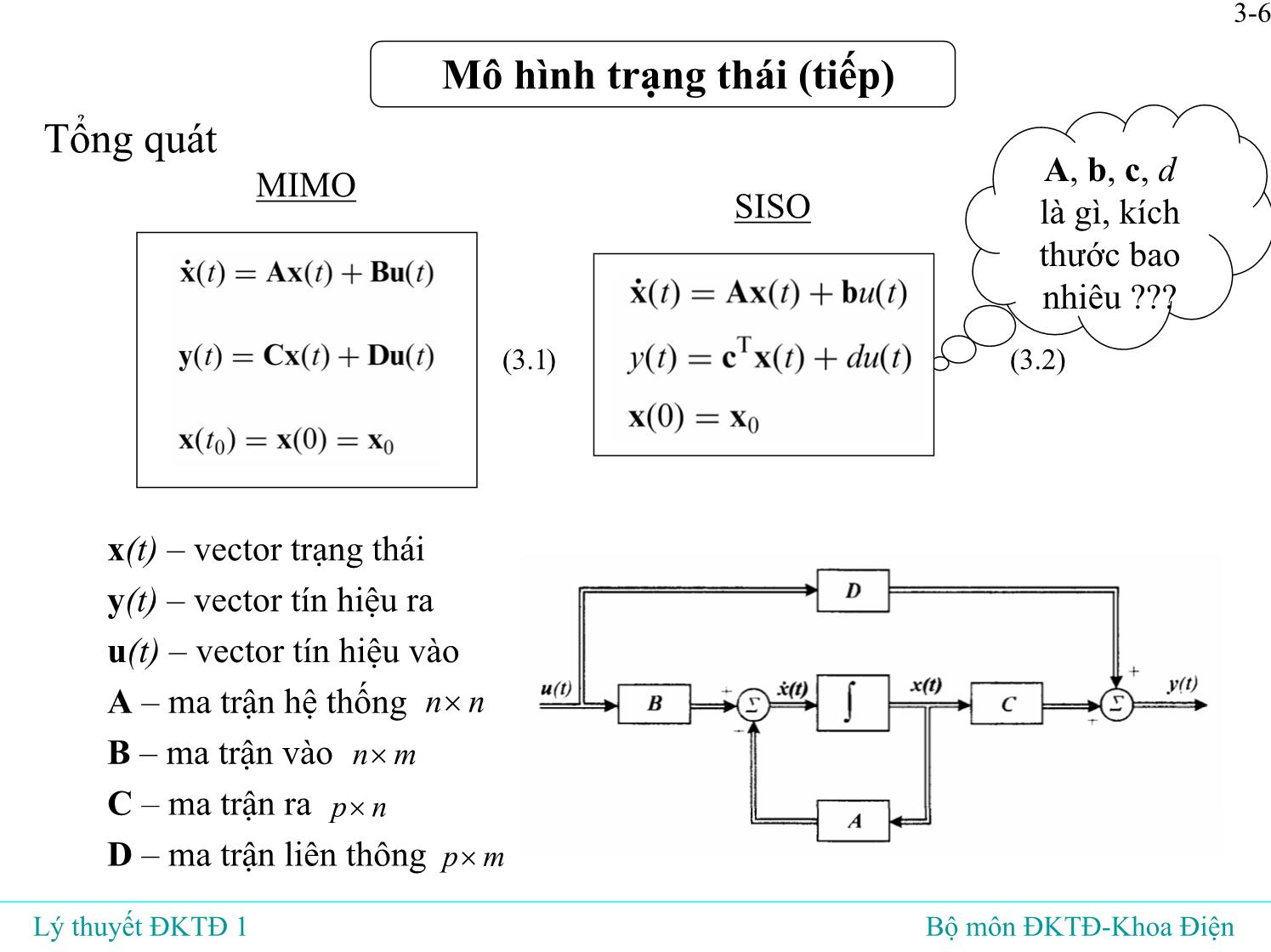
Tổng quát
MIMO
x(t) – vector trạng thái
y(t) – vector tín hiệu ra
u(t) – vector tín hiệu vào
A – ma trận hệ thống
B – ma trận vào
C – ma trận ra
D – ma trận liên thông
n n×
n m×
p n×
p m×
A, b, c, d
là gì, kích
thước bao
nhiêu ???
(3.1)
SISO
(3.2)
3-6
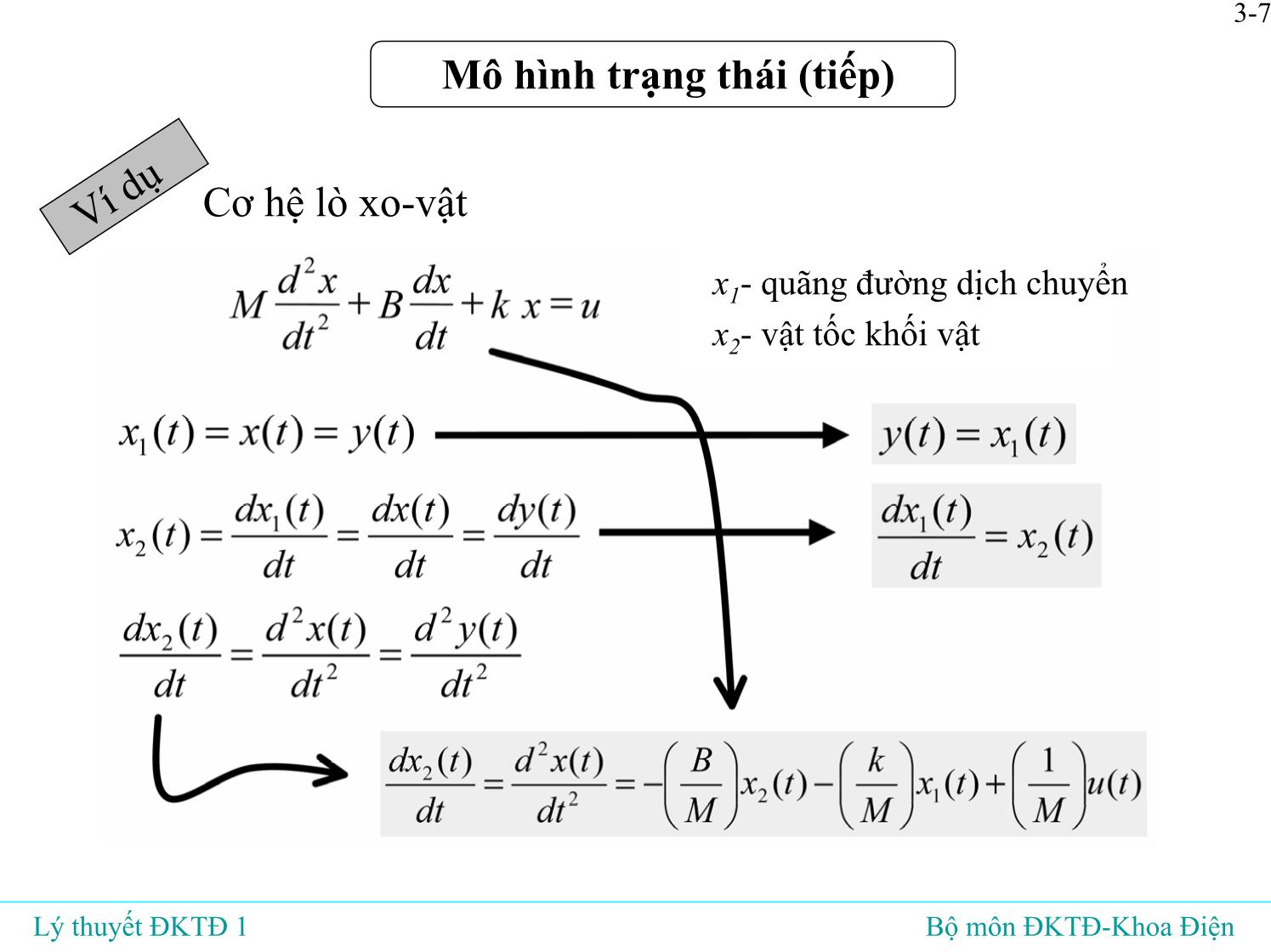
Mô hình trạng thái (tiếp)
Ví
dụ
3-7
Cơ hệ lò xo-vật
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
x1- quãng đường dịch chuyển
x2- vật tốc khối vật
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
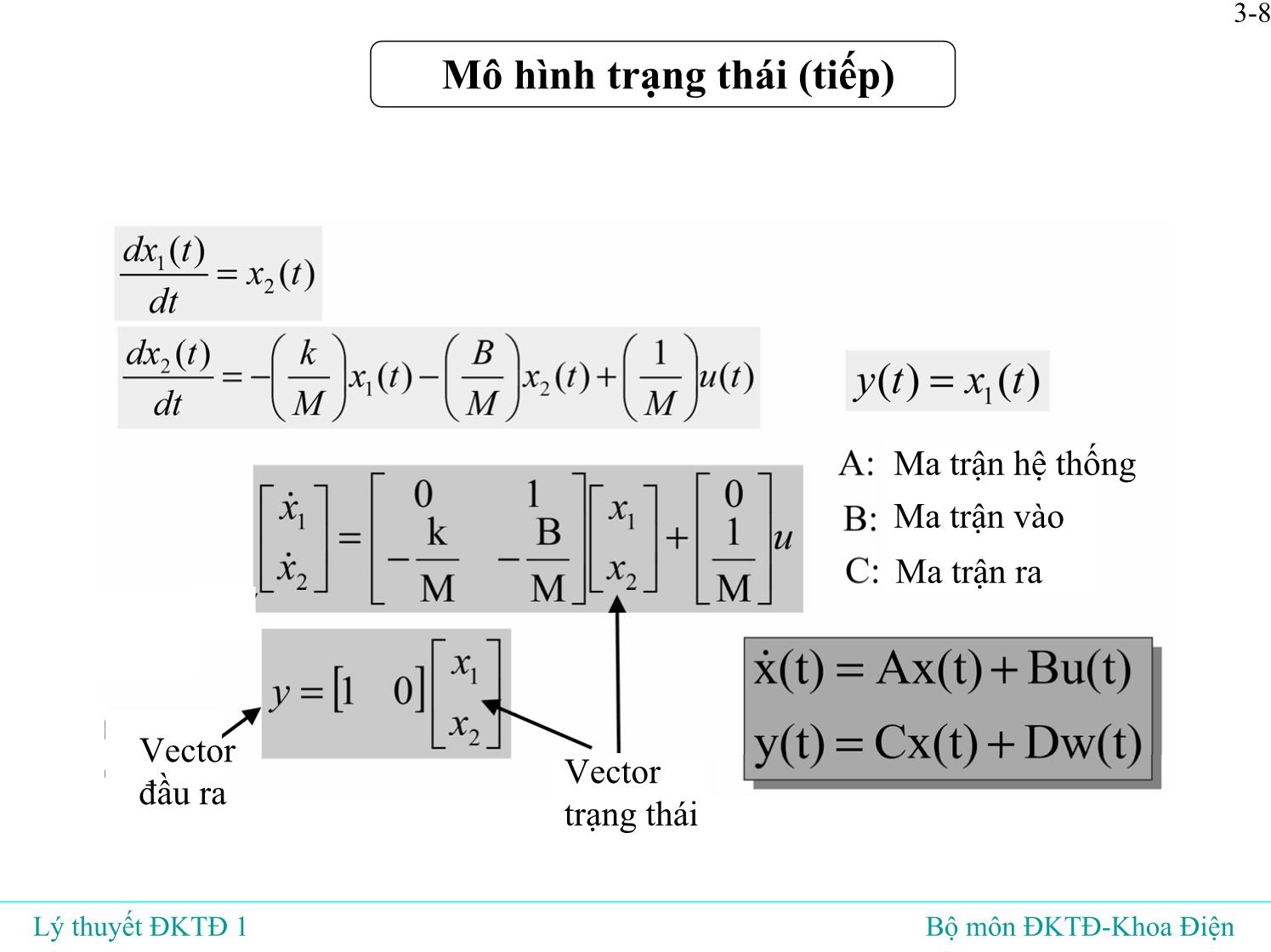
Mô hình trạng thái (tiếp)
3-8
Vector 
đầu ra Vector trạng thái
Ma trận hệ thống
Ma trận vào
Ma trận ra
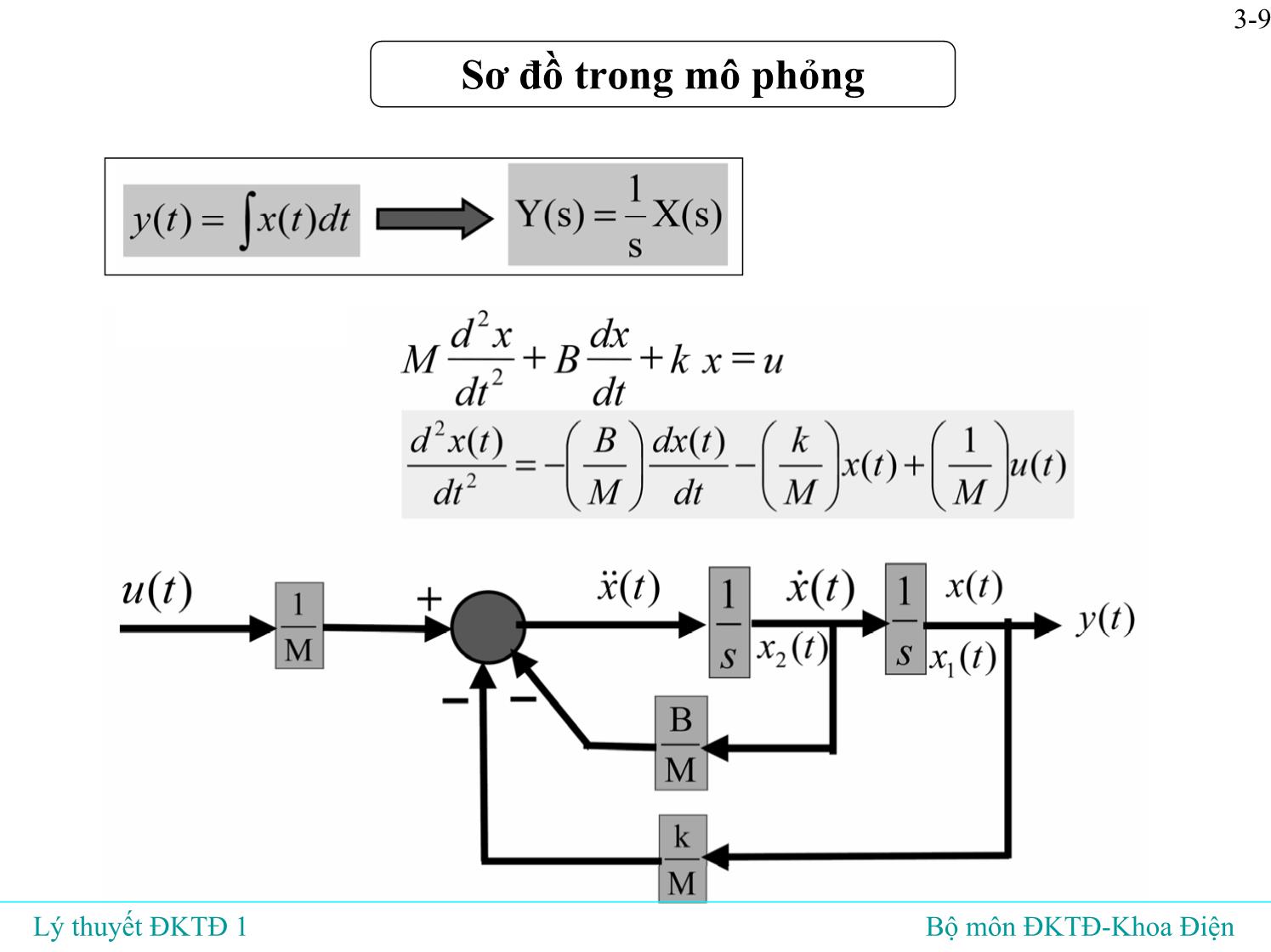
Sơ đồ trong mô phỏng
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
3-9
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Mô hình trạng thái (tiếp)
Bản chất
• Phân tích, thiết kế trên miền thời gian
• Phương trình vi phân bậc n mô tả đối tượng được chuyển thành hệ n
PTVP bậc nhất
• Bậc n thể hiện số phần tử độc lập tích lũy năng lượng trong hệ thống
Ưu điểm
• Thích hợp mô tả cho cả hệ phi tuyến, hệ tham số biến đổi theo
thời gian
• Cung cấp thông tin về trạng thái của đối tượng
• Tiện lợi khi phân tích thiết kế các hệ trích mẫu
3-10
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
Chuyển từ MHTT sang hàm truyền đạt
dẫn đến
3-11
Chuyển từ MHTT sang hàm truyền đạt
Ví
dụ
Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
3-12
Điểm không:
2+j1.7321 và
2-j1.7321
Điểm cực:
-1 và -2