Bài giảng Lý thuyết điều khiển tự động - Bài 15: Tính ổn định. Tính điều khiển được. Tính quan sát được - Đỗ Tú Anh
Ổn định BIBO
(2) (1)
Một hệ thống được gọi là ổn định BIBO nếu khi kích thích hệ bằng tín hiệu
u(t) bị chặn ở đầu vào thì hệ sẽ có đáp ứng y(t) ở đầu ra cũng bị chặn (tất cả
các điểm cực của hệ đều nằm ở nửa bên trái mặt phẳng phức s).
Từ (2) suy ra
Hệ (1) ổn định BIBO khi và chỉ khi ma trận A có tất cả các giá trị riêng
nằm bên trái trục ảo, tức là khi và chỉ khi
p( ) s s = − det( I A)
có tất cả các nghiệm có phần thực âm.
Có thể sử dụng các tiêu chuẩn Routh, Hurwitz được không???
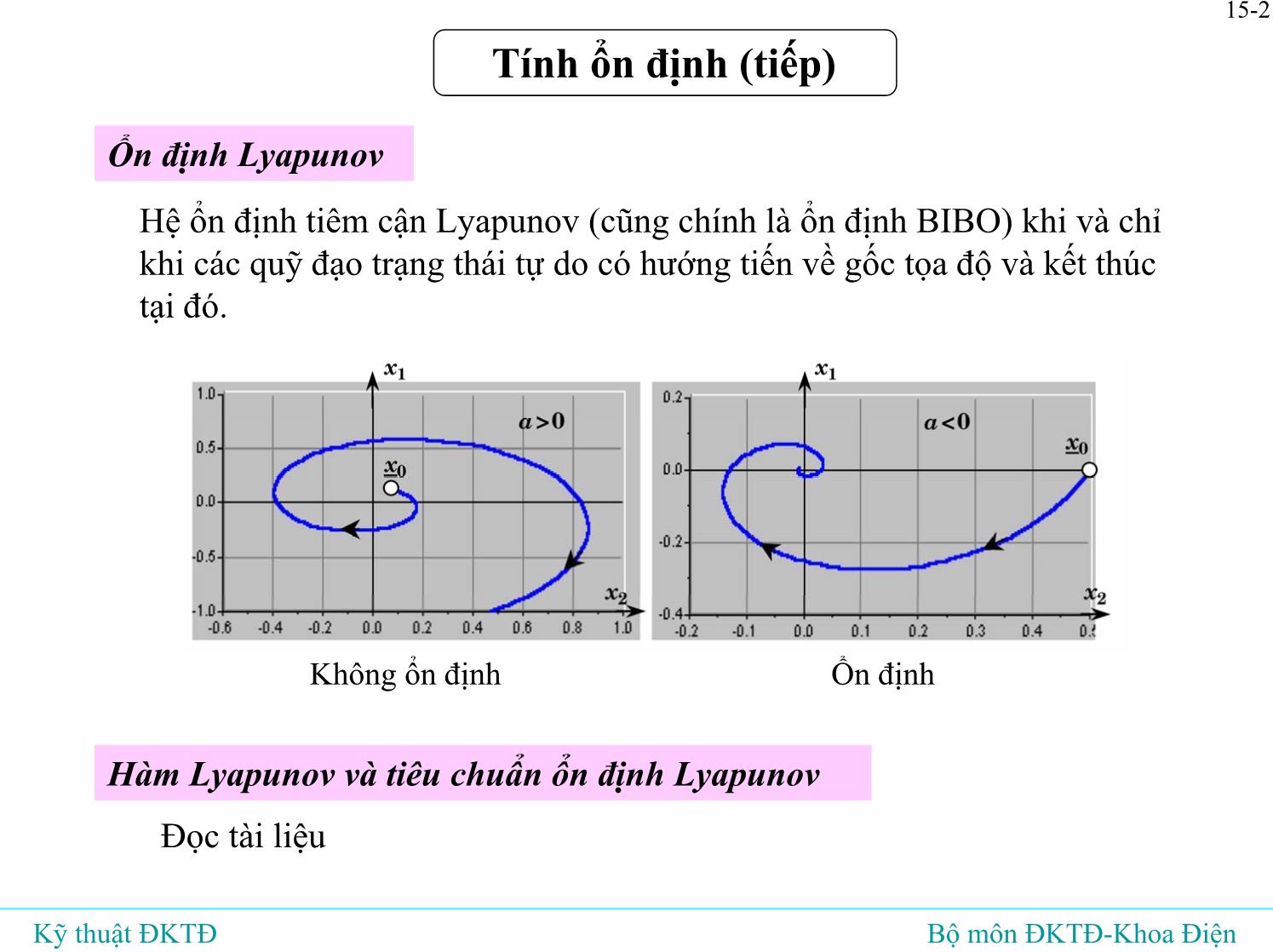
Ổn định Lyapunov
Hệ ổn định tiêm cận Lyapunov (cũng chính là ổn định BIBO) khi và chỉ
khi các quỹ đạo trạng thái tự do có hướng tiến về gốc tọa độ và kết thúc
tại đó.
Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Bạn đang xem tài liệu "Bài giảng Lý thuyết điều khiển tự động - Bài 15: Tính ổn định. Tính điều khiển được. Tính quan sát được - Đỗ Tú Anh", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết điều khiển tự động - Bài 15: Tính ổn định. Tính điều khiển được. Tính quan sát được - Đỗ Tú Anh

Kỹ thuật Điều khiển tự động Tính ổn định Tính điều khiển được Tính quan sát được ThS. Đỗ Tú Anh Bộ môn Điều khiển tự động Khoa Điện, Trường ĐHBK HN 15-1 Tính ổn định 1 ( )( ) ( ) det( ) adj sI AG s C sI A B D C B D sI A − −= − + = +− Ổn định BIBO (2) (1) Một hệ thống được gọi là ổn định BIBO nếu khi kích thích hệ bằng tín hiệu u(t) bị chặn ở đầu vào thì hệ sẽ có đáp ứng y(t) ở đầu ra cũng bị chặn (tất cả các điểm cực của hệ đều nằm ở nửa bên trái mặt phẳng phức s). Từ (2) suy ra Hệ (1) ổn định BIBO khi và chỉ khi ma trận A có tất cả các giá trị riêng nằm bên trái trục ảo, tức là khi và chỉ khi ( ) det( )p s sI A= − có tất cả các nghiệm có phần thực âm. Có thể sử dụng các tiêu chuẩn Routh, Hurwitz được không??? Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-2 Tính ổn định (tiếp) Ổn định Lyapunov Hệ ổn định tiêm cận Lyapunov (cũng chính là ổn định BIBO) khi và chỉ khi các quỹ đạo trạng thái tự do có hướng tiến về gốc tọa độ và kết thúc tại đó. Không ổn định Ổn định Hàm Lyapunov và tiêu chuẩn ổn định Lyapunov Đọc tài liệu Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-3 Tính điều khiển được Định nghĩa Một hệ thống tuyến tính liên tục đgl điều khiển được nếu tồn tại ít nhất một tín hiệu điều khiển đưa được nó từ một điểm trạng thái ban đầu 0x (tùy ý) về được gốc tọa độ 0 trong khoảng thời gian hữu hạn Hệ đgl điều khiển được hoàn toàn tại 0x nếu với một điểm trạng thái đích Tx (tùy ý), nhưng cho trước, luôn tồn tại một tín hiệu điều khiển ( )u t đưa hệ từ 0x tới được Tx trong khoảng thời gian hữu hạn Tiêu chuẩn Kalman Cần và đủ để hệ liên tục tuyến tính (1) điều khiển được là Ma trận điều khiển được Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-4 Tính điều khiển được (tiếp) Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-5 Tính quan sát được Ý nghĩa • Trong điều khiển hồi tiếp, tín hiệu điều khiển được tính toán dựa trên thông tin hồi tiếp của các tín hiệu ra và các tín hiệu trạng thái • Không phải mọi tín hiệu đều có thể đo được trực tiếp bằng cảm biến mà chỉ có thể có được một cách gián tiếp thông qua các tín hiệu đo được khác Quan sát một tín hiệu được hiểu là công việc xác định tín hiệu thông qua đo trực tiếp hoặc gián tiếp qua các tín hiệu đo được khác (thường là các tín hiệu vào ra) Định nghĩa Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-6 Tính quan sát được (tiếp) Định nghĩa (tiếp) Nếu hệ (1) quan sát được tại thời điểm t0 thì nó cũng quan sát được tại mọi thời điểm t ≠ 0 Tiêu chuẩn Kalman Cần và đủ để hệ liên tục tuyến tính (1) quan sát được là Ma trận quan sát được Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện 15-7 Tính quan sát được (tiếp) Kỹ thuật ĐKTĐ Bộ môn ĐKTĐ-Khoa Điện
File đính kèm:
 bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_15_tinh_on_dinh_t.pdf
bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_15_tinh_on_dinh_t.pdf

