Bài giảng Lý thuyết điều khiển tự động - Bài 12: Ziegler-Nichols. Tối ưu độ lớn. Tối ưu đối xứng - Đỗ Tú Anh
Phương pháp Ziegler-Nichols
Đặc điểm của phương pháp
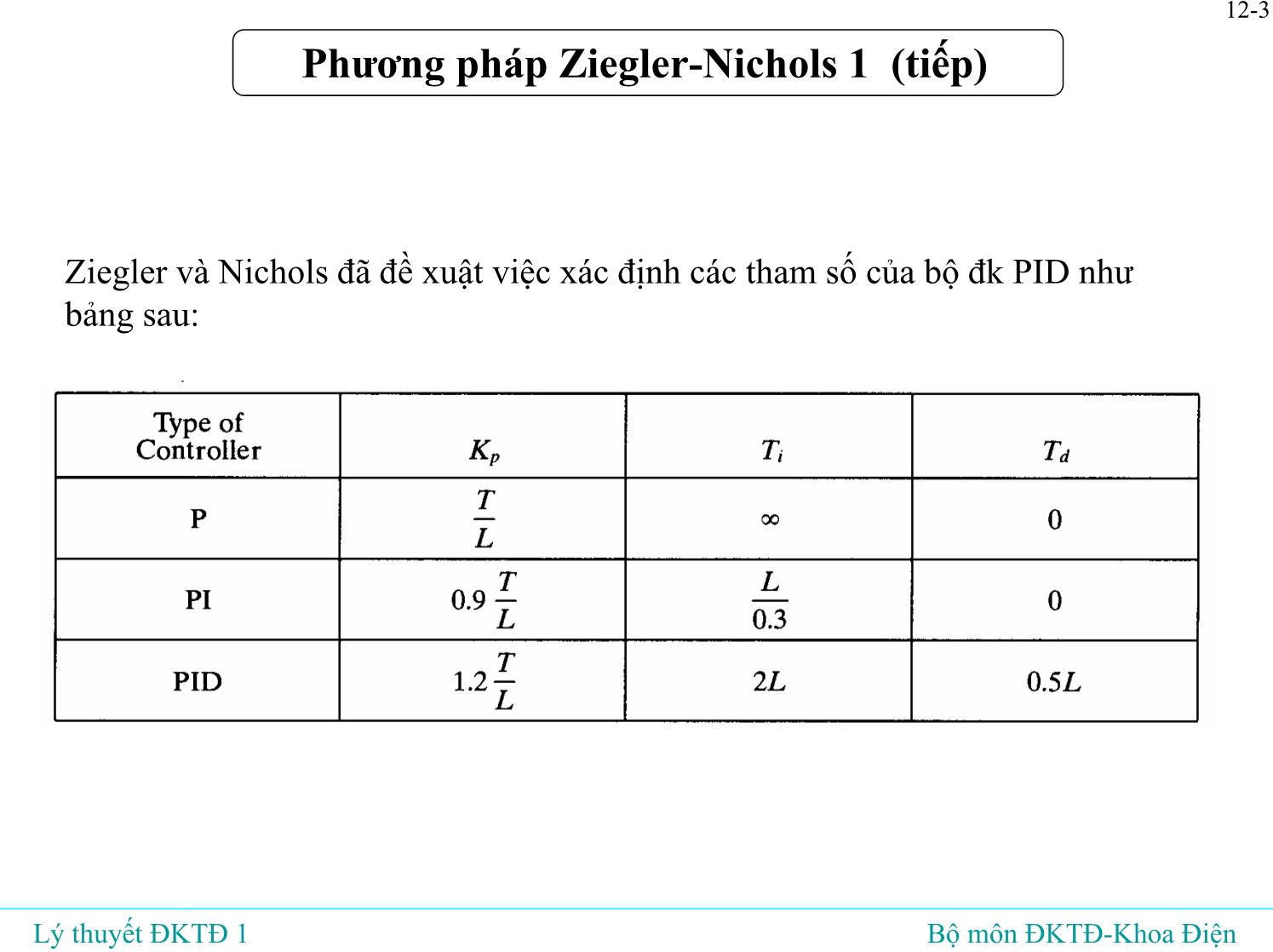
• Là phương pháp thực nghiệm để xác định các tham số của bộ đk PID
• Rất thuận tiện khi mô hình toán học của đối tượng chưa biết trước
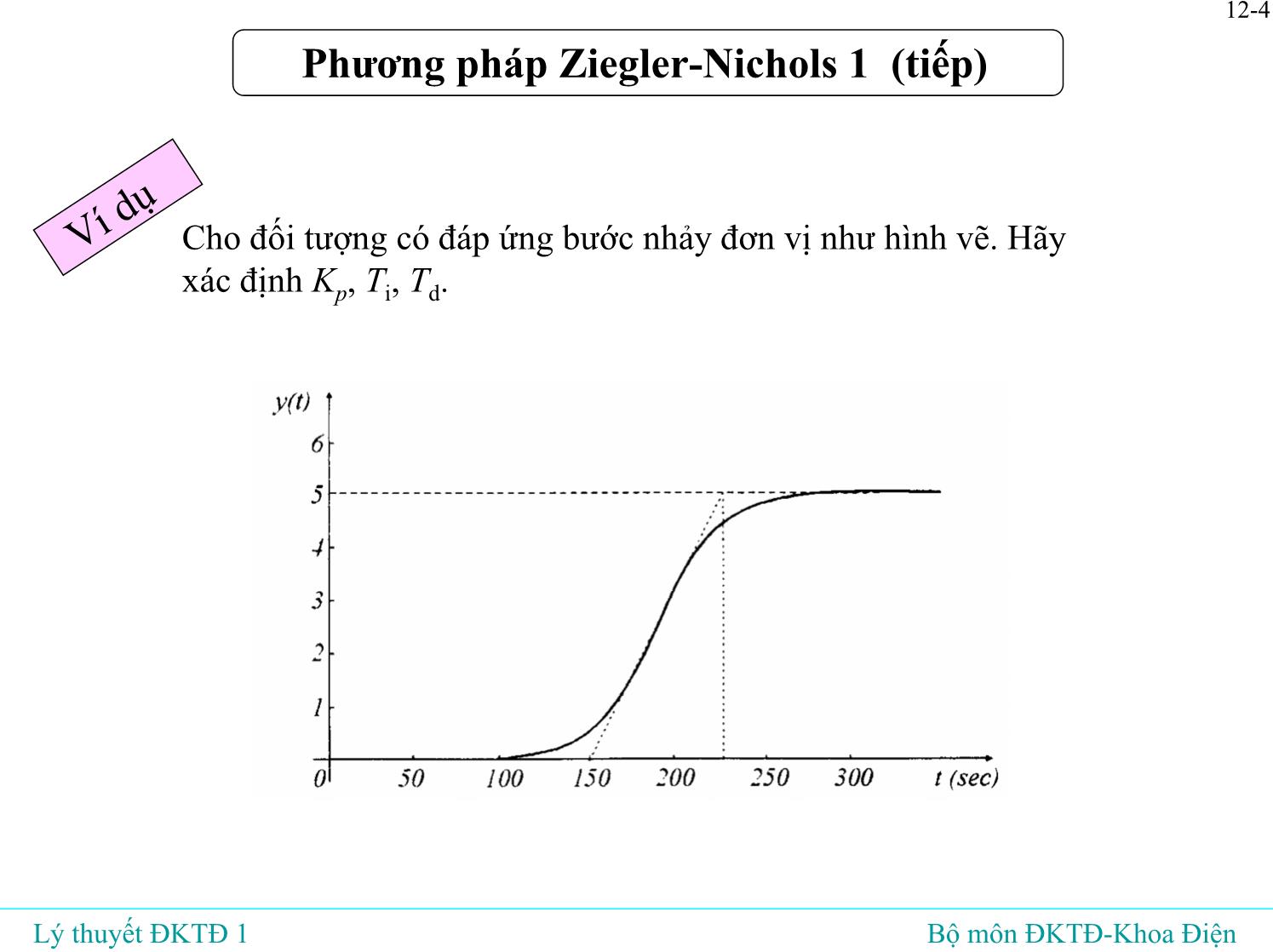
• Đáp ứng nhận được có độ quá điều chỉnh khoảng 25%
Phương pháp Ziegler-Nichols 1
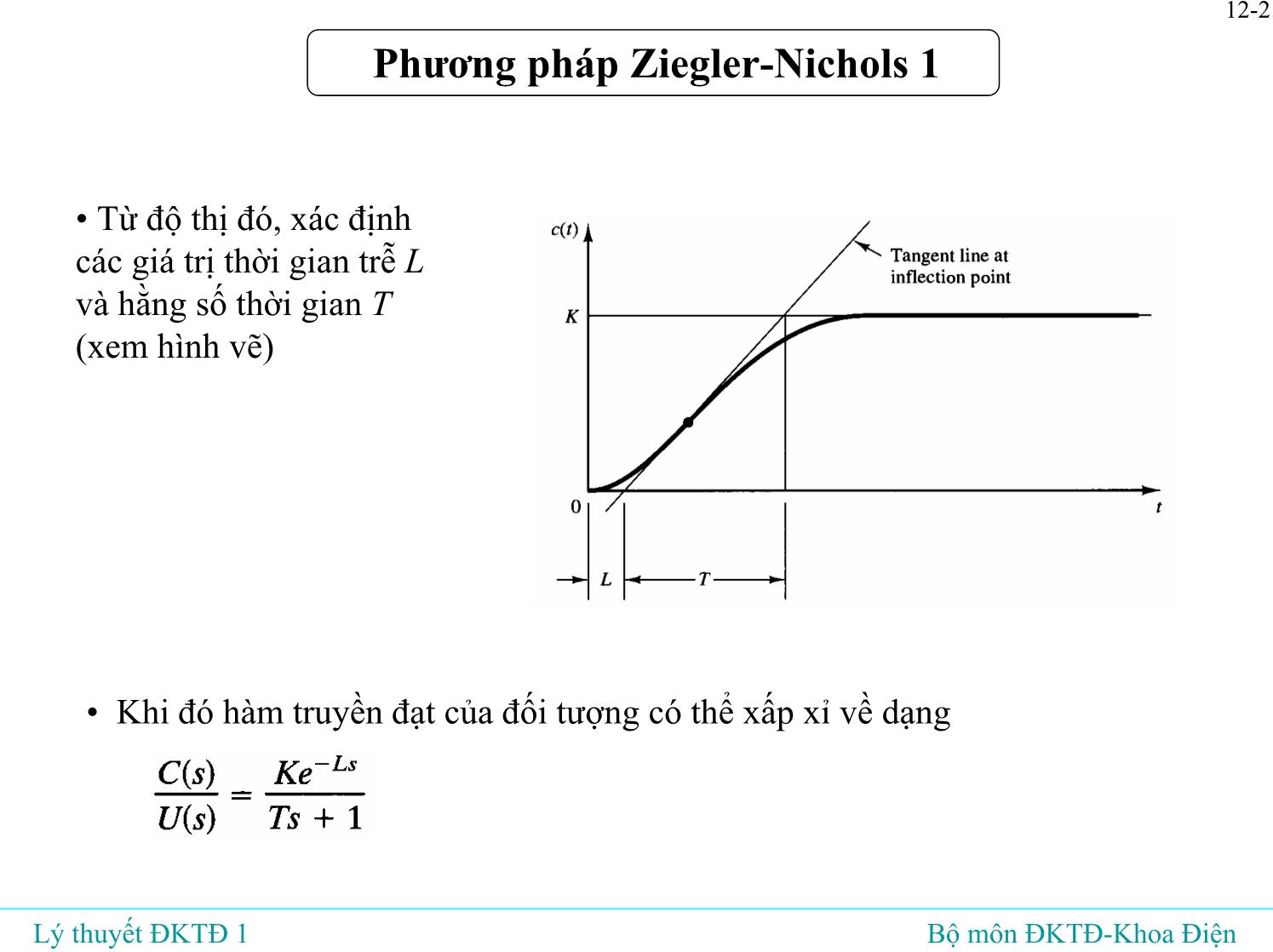
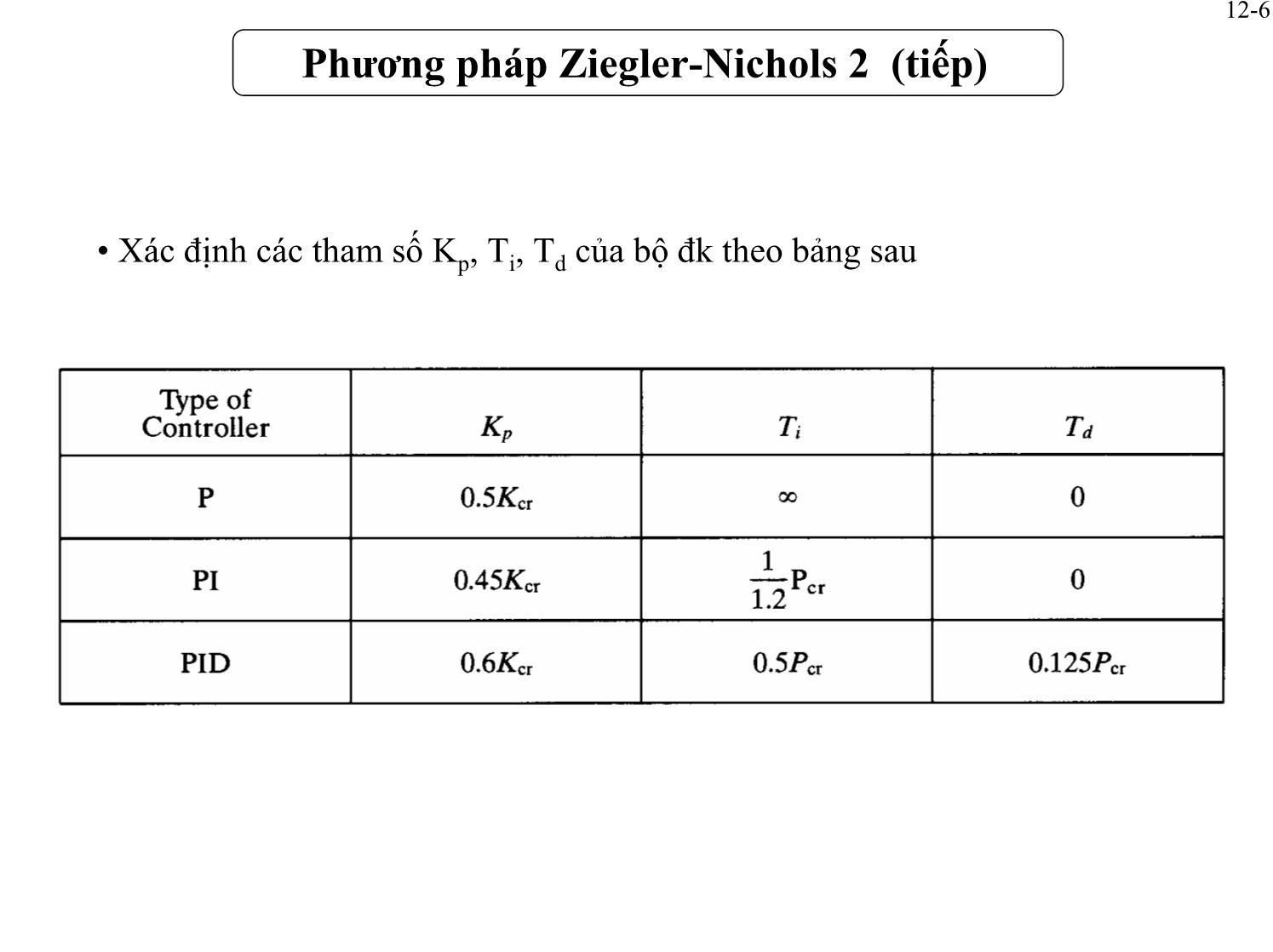
• Xác định bằng thực nghiệm
đáp ứng bước nhảy của đối
tượng
• Nếu đáp ứng có dạng hình chữ
S thì áp dụng được phương
pháp này
Phương pháp Ziegler-Nichols 2
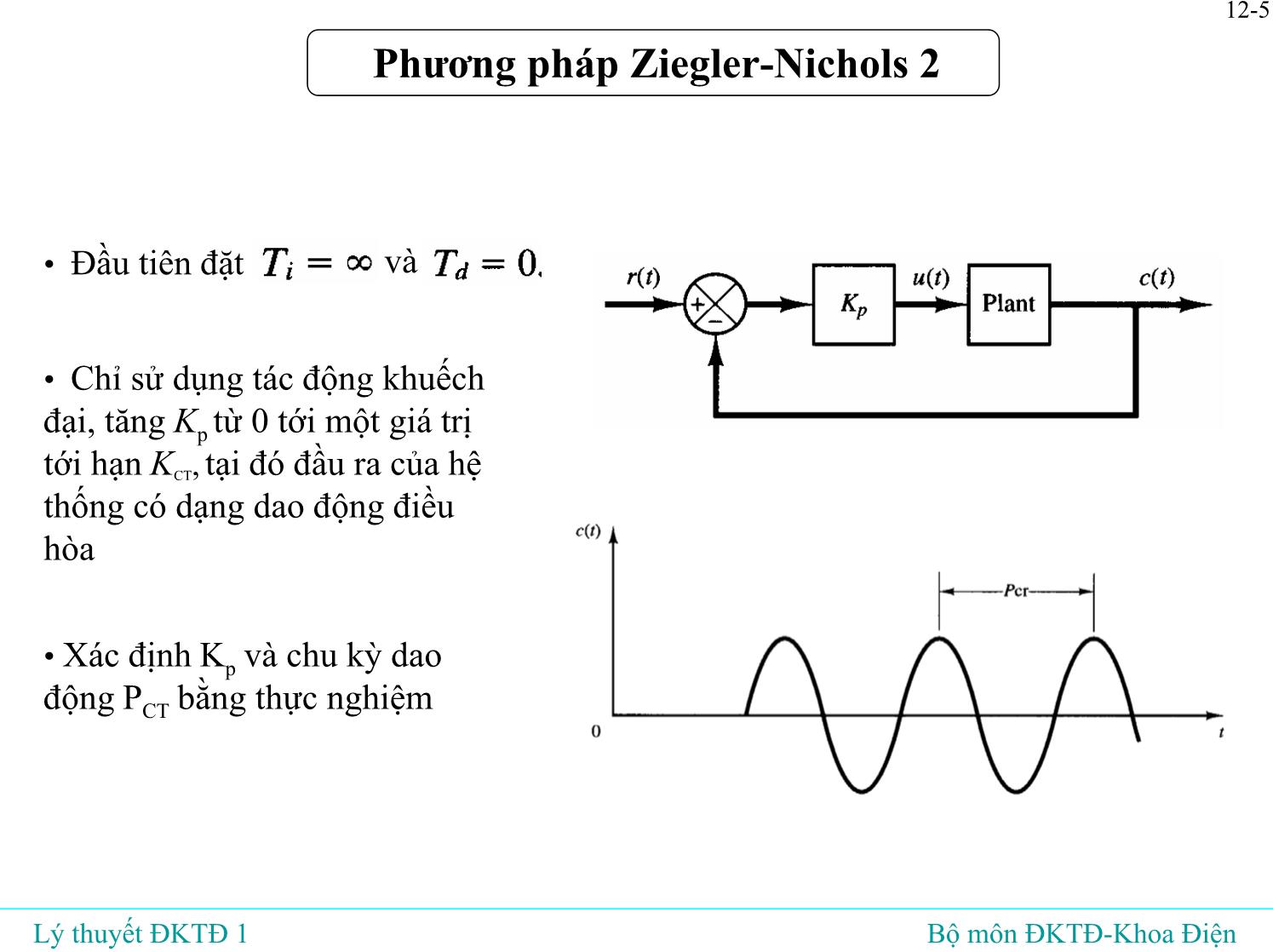
• Đầu tiên đặt và
• Chỉ sử dụng tác động khuếch
đại, tăng Kp từ 0 tới một giá trị
tới hạn KCT, tại đó đầu ra của hệ
thống có dạng dao động điều
hòa
• Xác định K
p và chu kỳ dao
động PCT bằng thực nghiệm

Trang 1

Trang 2
Trang 3
Trang 4
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Lý thuyết điều khiển tự động - Bài 12: Ziegler-Nichols. Tối ưu độ lớn. Tối ưu đối xứng - Đỗ Tú Anh", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết điều khiển tự động - Bài 12: Ziegler-Nichols. Tối ưu độ lớn. Tối ưu đối xứng - Đỗ Tú Anh

Lý thuyết Điều khiển tự động 1 Ziegler-Nichols Tối ưu độ lớn Tối ưu đối xứng ThS. Đỗ Tú Anh Bộ môn Điều khiển tự động Khoa Điện, Trường ĐHBK HN 12-1 Phương pháp Ziegler-Nichols Đặc điểm của phương pháp • Là phương pháp thực nghiệm để xác định các tham số của bộ đk PID • Rất thuận tiện khi mô hình toán học của đối tượng chưa biết trước • Đáp ứng nhận được có độ quá điều chỉnh khoảng 25% Phương pháp Ziegler-Nichols 1 • Xác định bằng thực nghiệm đáp ứng bước nhảy của đối tượng • Nếu đáp ứng có dạng hình chữ S thì áp dụng được phương pháp này Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-2 Phương pháp Ziegler-Nichols 1 • Từ độ thị đó, xác định các giá trị thời gian trễ L và hằng số thời gian T (xem hình vẽ) • Khi đó hàm truyền đạt của đối tượng có thể xấp xỉ về dạng Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-3 Phương pháp Ziegler-Nichols 1 (tiếp) Ziegler và Nichols đã đề xuật việc xác định các tham số của bộ đk PID như bảng sau: Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-4 Phương pháp Ziegler-Nichols 1 (tiếp) Cho đối tượng có đáp ứng bước nhảy đơn vị như hình vẽ. Hãy xác định Kp, Ti, Td. Ví dụ Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-5 Phương pháp Ziegler-Nichols 2 • Đầu tiên đặt và • Chỉ sử dụng tác động khuếch đại, tăng Kp từ 0 tới một giá trị tới hạn KCT, tại đó đầu ra của hệ thống có dạng dao động điều hòa • Xác định Kp và chu kỳ dao động PCT bằng thực nghiệm Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-6 Phương pháp Ziegler-Nichols 2 (tiếp) • Xác định các tham số Kp, Ti, Td của bộ đk theo bảng sau 12-7 Phương pháp Ziegler-Nichols Một vài nhận xét • Phương pháp Ziegler Nichols thật sự hữu ích khi mô hình toán học của đối tượng không biết trước, nhưng vẫn rất hiệu quả ngay cả khi đã biết MHTH của đối tượng • Trong trường hợp chất lượng điều khiển chưa được như mong muốn, có thể tinh chỉnh các tham số của bộ PID • Nói chung những đối tượng động học phức tạp và không chứa thành phần tích phân có thể áp dụng phương pháp này. Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-8 Phương pháp Ziegler-Nichols Ví dụ về đối tượng có chứa một thành phần tích phân không thể áp dụng phương pháp Ziegler-Nichols Do có chứa một thành phần tích phân nên không áp dụng được pp Ziegler- Nichols 1 Nếu thử áp dụng pp Ziegler-Nichols 2, sẽ không có giá trị Kp nào của bộ điều khiển P để đáp ứng của cả hệ thống đạt tới chế độ dao động ở biên giới ổn định. Để chứng minh điều này, trước hết ta xét phương trình đặc tính của hệ kín Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-9 Phương pháp Ziegler-Nichols hay Lập bảng Routh Các hệ số trong cột đầu tiên luôn dương với mọi Kp > 0. Do đó không có giá trị nào của K để hệ đạt tới chế độ dao động ở biên giới ổn định Không áp dụng được pp Ziegler-Nichols 2 Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-10 Các phương pháp trên miền tần số Đặt vấn đề Xét hệ thống đk có hàm truyền đạt hệ kín Mong muốn đáp ứng r(t) giống như tín hiệu đặt c(t) tại mọi điểm tần số Nói cách khác (1) Trên thực tế, người ta thỏa mãn với việc thiết kế R(s) mang lại tính chất (1) trong dải tần số thấp. Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-11 Phương pháp tối ưu độ lớn Bộ điều khiển PID tối ưu độ lớn Là bộ điều khiển R(s) thỏa mãn trong dải tần số thấp có độ rộng lớn Phạm vi ứng dụng Hàm truyền đạt của đối tượng có dạng Đối tượng phải ổn định Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-12 Phương pháp tối ưu độ lớn (tiếp) Ví dụ Hàm truyền đạt hệ hở Hàm truyền đạt hệ kín Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-13 Phương pháp tối ưu độ lớn (tiếp) Chọn TR sao cho Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện Bộ đk ITổng quát Bộ đk PI Bộ đk PID 12-14 Phương pháp tối ưu độ lớn (tiếp) Câu hỏi 1. Các tham số kp, Ti (cho bộ đk PI) và các tham số kp, Ti, Td (cho bộ đk PID) được xác định như thế nào? 2. Làm thế nào để thiết kế bộ đk cho đối tượng có hàm truyền đạt: 3. Hạn chế của phương pháp? Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-15 Phương pháp tối ưu đối xứng Bộ điều khiển PID tối ưu đối xứng Là bộ điều khiển R(s) thỏa mãn trong dải tần số thấp và có đồ thị Bode của hàm truyền đạt hệ hở như hình vẽ bên Phạm vi ứng dụng Hàm truyền đạt của đối tượng có dạng Đối tượng không ổn định Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-16 Phương pháp tối ưu đối xứng (tiếp) Bộ đk PI(2) (2) Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện 12-17 Phương pháp tối ưu đối xứng (tiếp) Bộ đk PID Lý thuyết ĐKTĐ 1 Bộ môn ĐKTĐ-Khoa Điện
File đính kèm:
 bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_12_ziegler_nichol.pdf
bai_giang_ly_thuyet_dieu_khien_tu_dong_bai_12_ziegler_nichol.pdf

