Bài giảng Đầu tư tài chính - Chương 8: Độ nhạy cảm của giá trái phiếu với lãi suất - Trần Thị Thái Hà

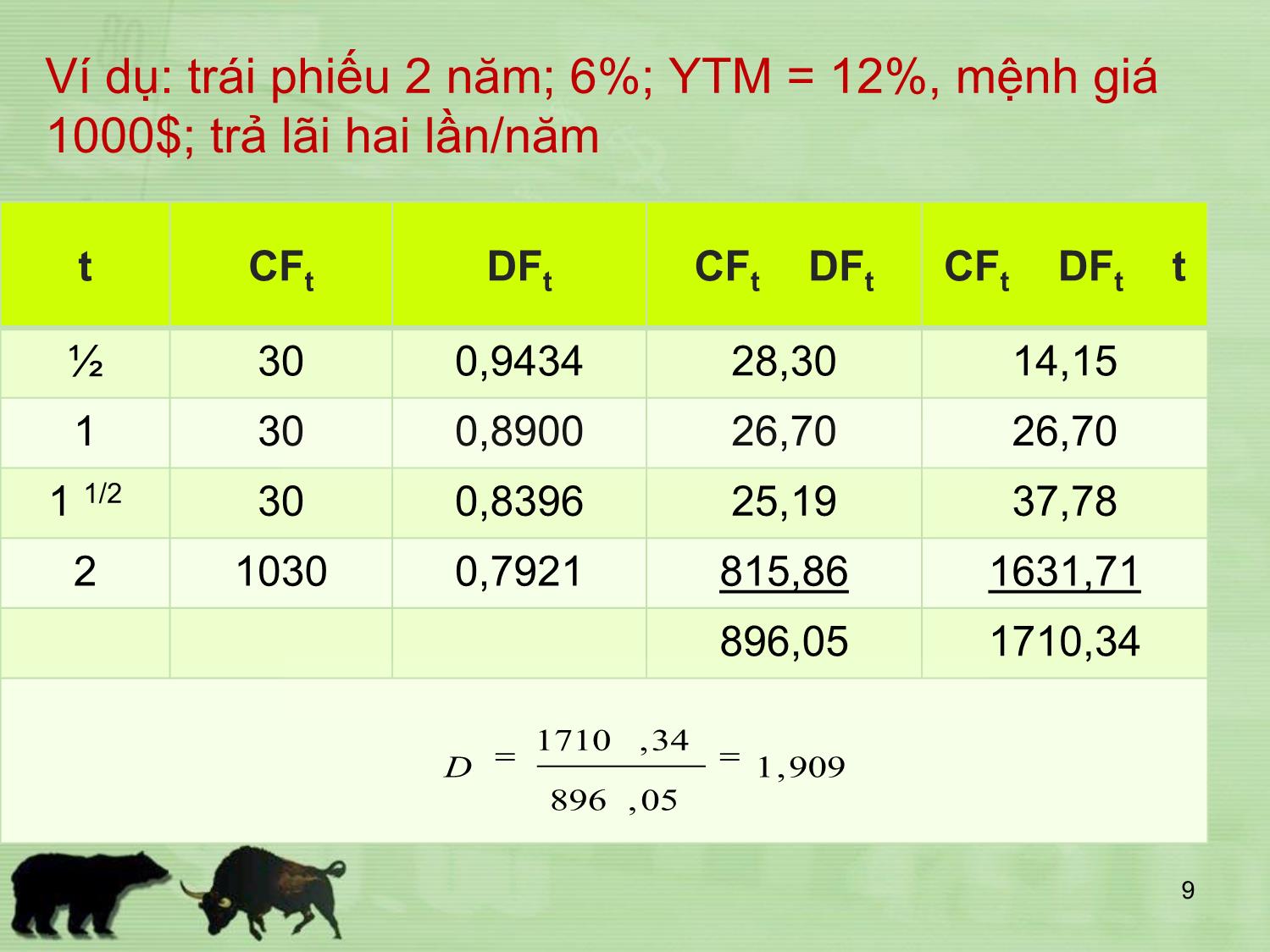
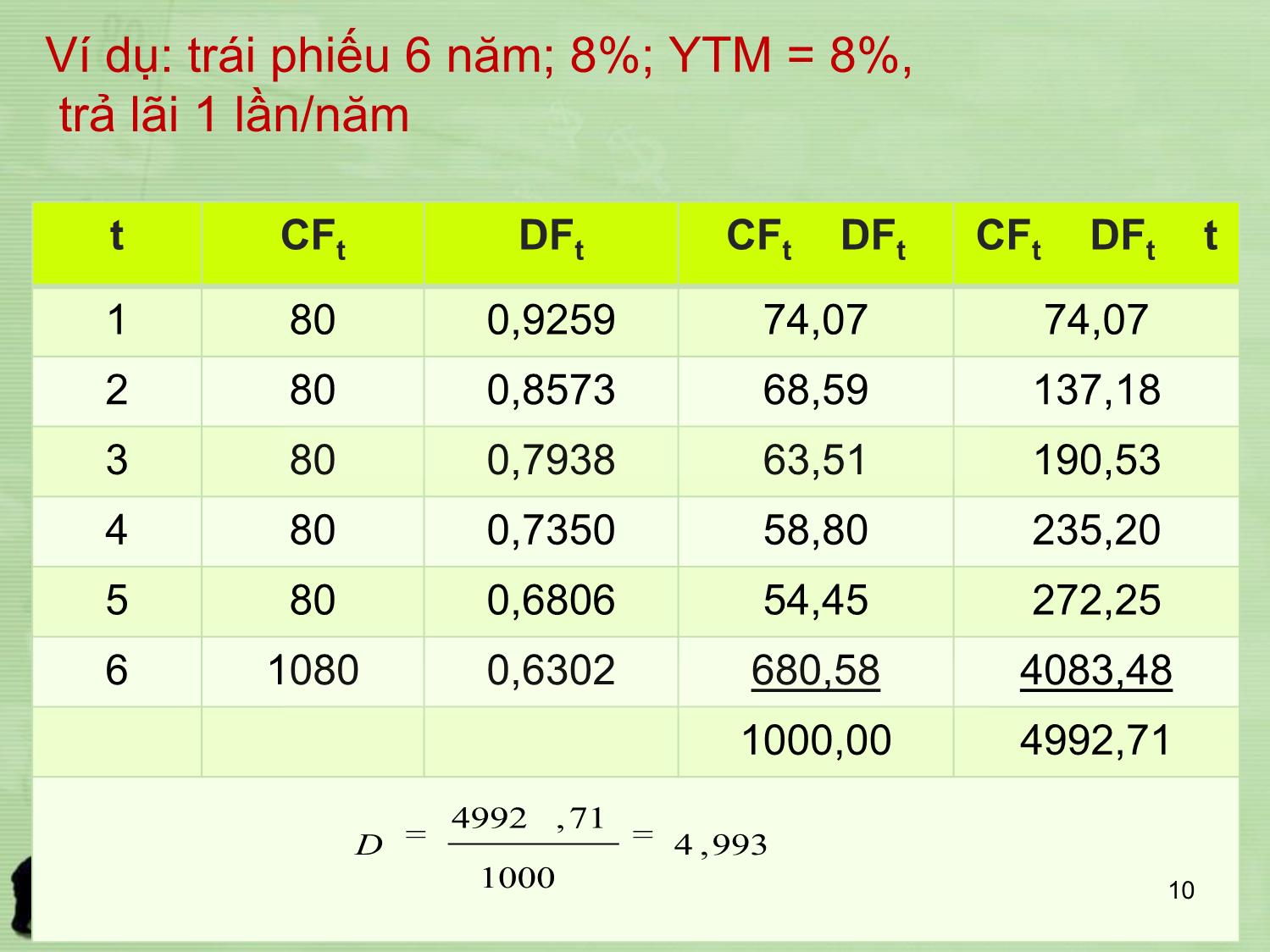
Độ nhạy cảm của giá trái phiếu 
với lãi suất
Chương 8
Rủi ro lãi suất
• Giá và lãi suất của trái phiếu có quan hệ 
ngược chiều → lãi suất thay đổi thì người 
nắm giữ trái phiếu sẽ có lời hoặc bị lỗ.
• Vì sao giá trái phiếu lại phản ứng với biến 
động lãi suất? Để có thể tồn tại trong một thị 
trường cạnh tranh.
• Mức độ phản ứng của giá trái phiếu với sự 
thay đổi lãi suất là mối quan tâm lớn của nhà 
đầu tư.
Mối quan hệ tổng quát
• Lãi suất , giá ; Lãi suất , giá .
• YTM của một trái phiếu tăng dẫn tới một thay 
đổi giá nhỏ hơn so với một mức giảm YTM với 
quy mô tương đương.
Mối quan hệ này đúng với bất kỳ trái phiếu 
nào (dạng thông thường).
Tuy nhiên, mức độ biến động của giá với cùng 
một thay đổi lãi suất sẽ khác nhau giữa các 
trái phiếu khác nhau.
Độ nhạy cảm với lãi suất
• Quan sát hai trái phiếu giống nhau về mọi 
phương diện, trừ thời gian đáo hạn.
– Giá của trái phiếu dài hạn nhạy cảm với thay đổi 
lãi suất hơn là giá của trái phiếu ngắn hạn.
• Tuy nhiên, độ nhạy cảm của giá trái phiếu 
với những thay đổi của lãi suất tăng với một 
tỷ lệ giảm dần khi thời gian đáo hạn tăng lên. 
(Nói cách khác, rủi ro lãi suất tăng chậm hơn so 
với mức tăng lên của thời hạn).
• Hai trái phiếu giống nhau về mọi phương 
diện, trừ lãi suất cuống phiếu
– Trái phiếu có lãi suất cuống phiếu thấp hơn sẽ có 
giá nhạy cảm hơn với thay đổi lãi suất, so với của 
trái phiếu có lãi suất cuống phiếu cao.
• Độ nhạy cảm của giá trái phiếu với một thay 
đổi của lãi suất liên quan ngược chiều với 
mức YTM tại đó trái phiếu đang được bán.
Macaulay Duration
• Chỉ riêng thời gian đáo hạn thì không đủ để 
phản ánh độ nhạy cảm với lãi suất của giá trái 
phiếu. 
• Zero và trái phiếu trả lãi định kỳ có cùng thời 
hạn?.
• Macaulay (1938) phát triển một thước đo mới, 
phản ánh được tất cả các yếu tố tác động tới 
phản ứng của giá trái phiếu với lãi suất: 
Duration.
Tính Duration
• Công thức
• Quy trình
1. Tính PV của từng khoản lãi và gốc [PV(CFt)], 
chiết khấu theo YTM hiện hành.
2. Chia PV này cho giá hiện hành (P)
3. Nhân giá trị tương đối này với năm nhận được 
dòng tiền (t).
4. Lặp lại các bước từ 1-3 cho từng năm, rồi cộng 
tất cả các giá trị tính được ở bước 3.
T
t
t
t
P
CFPV
D
1
)(
• Giải thích công thức
D của một trái phiếu là thước đo thời gian đáo hạn 
thực sự của trái phiếu, được định nghĩa là bình 
quân gia quyền của các khoảng thời gian (t) cho 
tới khi nhận được các khoản thanh toán, với trọng 
số (wt) = PV (CFt)/P = [CFt/(1+y)
t]/P.
• Một cách viết khác
T
t
t
wtD
1
Ví dụ: trái phiếu 2 năm; 6%; YTM = 12%, mệnh giá 
1000$; trả lãi hai lần/năm
t CFt DFt CFt DFt CFt DFt t
½ 30 0,9434 28,30 14,15
1 30 0,8900 26,70 26,70
1 1/2 30 0,8396 25,19 37,78
2 1030 0,7921 815,86 1631,71
896,05 1710,34
9
909,1
05,896
34,1710
D
Ví dụ: trái phiếu 6 năm; 8%; YTM = 8%,
trả lãi 1 lần/năm
t CFt DFt CFt DFt CFt DFt t
1 80 0,9259 74,07 74,07
2 80 0,8573 68,59 137,18
3 80 0,7938 63,51 190,53
4 80 0,7350 58,80 235,20
5 80 0,6806 54,45 272,25
6 1080 0,6302 680,58 4083,48
1000,00 4992,71
10
993,4
1000
71,4992
D
Ý nghĩa của Duration
• Là một thước đo đơn giản về thời gian đáo 
hạn bình quân có hiệu lực của một danh mục.
• Là công cụ quan trọng để cách ly các danh 
mục khỏi rủi ro lãi suất.
• Là thước đo tính nhạy cảm của một danh mục 
trái phiếu.
Sử dụng D: ước tính biến động giá 
trái phiếu
• Chỉ áp dụng cho những dao động tương đối 
nhỏ của lãi suất thị trường.
• Quan hệ giữa giá trái phiếu và thay đổi lãi 
suất
yD
P
P
y
D
D
y
y
D
P
P
*
1
*
;
1
%
Các yếu tố quy định Duration
• Lãi suất cuống phiếu cao hơn: D nhỏ hơn
• Thời gian đáo hạn dài hơn: D lớn hơn
• YTM cao hơn: D nhỏ hơn.
• Với trái phiếu zero, D = M
• Với trái phiếu vĩnh viễn D = 1 + (1/y)
• D của một danh mục trái phiếu DP = ∑WiDi
•
Giá
Lãi suất thị trường
Y*Y1
P*
P1
P1’
Sai số
Hạn chế của D
• Nếu ∆P/P = -D*∆y, đồ thị quan hệ giá-lãi suất 
phải là đường thẳng, nhưng trên thực tế, nó là 
đường cong.
• Sử dụng D để ước tính % thay đổi giá: chỉ áp 
dụng được với những biến động nhỏ của lãi 
suất.
• Sai số xuất hiện khi biến động lãi suất là 
tương đối lớn.
Convexity (Độ lồi)
• Thước đo D không áp dụng với những thay 
đổi lãi suất lớn. 
• Độ lồi là thước đo “tính lồi” (curvature) của 
mối quan hệ giá-lợi suất, cho biết đường cong 
này đi chệch ra khỏi mức gần đúng theo 
đường thẳng của nó bao nhiêu.
16
Công thức tính
17
21232
2
2
1
22
2
)1(
)/100)(1(
)1(
2
)1(
1
1
2
)1(
)1(
)1(
)1(
nnn
n
n
t
t
y
yCnn
yy
Cn
yy
C
dy
Pd
y
Mnn
y
Ctt
dy
Pd
Ước tính ∆P (%) với D và C
• Thay đổi giá do Độ lồi = ½ x Convexity x (∆y)2
Ước tính thay đổi giá với một dao động lớn 
của lãi suất: sử dụng cả D và C:
% thay đổi giá = % thay đổi giá do D + % thay 
đổi giá do C
18
Ba điểm lưu ý với Convexity
• Convexity và thước đo Convexity
• Cách giải thích Convexity so với Duration: 
không giống nhau.
D= 4 và C = 182,92?
• Định nghĩa và cách tính thước đo C có thể 
khác nhau chút ít, nhưng mối quan hệ giữa C 
và % thay đổi giá là như nhau.
19
So sánh độ lồi của hai trái phiếu
Lãi suất thị trường
Giá
TP A
TP B
TP B
TP A
Độ lồi của TP B > Độ lồi của TP A
20
• Hai trái phiếu A và B có cùng D, chào cùng 
mức lợi suất, nhưng độ lồi khác nhau.
• Luôn luôn có PB > PA: Trái phiếu B tăng giá 
mạnh hơn khi lợi suất giảm và mất giá ít hơn 
khi lợi suất tăng.
• Giá của B sẽ cao hơn → lợi suất thấp hơn.
Câu hỏi: Nhà đầu tư sẵn sàng trả giá bao 
nhiêu cho độ lồi?
21
Đặc tính của độ lồi
• TP có C lớn sẽ có giá cao hơn, bất kể Ls thị 
trường ↑↓, →lợi suất sẽ thấp hơn.
• Khi lợi suất đòi hỏi tăng (giảm), độ lồi sẽ giảm 
(tăng). (Độ lồi dương).
• Với một lợi suất và thời hạn xác định, lãi suất 
cuống phiếu càng thấp, độ lồi của một trái 
phiếu càng lớn.
• Với một lợi suất và D* xác định, lãi suất cuống 
phiếu càng thấp, độ lồi càng nhỏ.
22
Sử dụng D: “tiêm phòng”
Ví dụ: 
• Năm 2004, Cty bảo hiểm cam kết thanh toán 
sau 5 năm cho người về hưu, trọn gói là 
1469$; tương đương với đầu tư 1000$ với 
lãi suất kép hàng năm 8% trong 5 năm.
• Khoản đầu tư nào đem lại 1469$ bất chấp lãi 
suất biến động như thế nào trong tương lai?
• Xem xét hai phương án
23
1. Mua trái phiếu Zero thời hạn 5 năm
P = 1000$/(1,08)5 = 680,58$; khối lượng 
mua được: 1000/680,58 (trái phiếu)
D = M
Không có dòng tiền giữa kỳ, không có hiệu 
ứng của thay đổi lãi suất giữa kỳ lên thu 
nhập do tái đầu tư 
 Khoản đầu tư đem lại chính xác 1469$.
24
2. Mua trái phiếu trả lãi định kỳ, có D = 5 năm 
(ví dụ trên)
• Nếu lãi suất vẫn là 8% trong 5 năm: Dòng tiền 
Cty bảo hiểm nhận được 
Lãi cuống phiếu, 5 80$ = 400$
Thu tái đầu tư : 80 FVA (8%;5) – 400= 69$
Giá bán trái phiếu vào cuối năm 5: 1000$
Tổng: 1469$
25
• Nếu lãi suất giảm còn 7 % trong 5 năm:
Lãi cuống phiếu: 5 80$ = 400$
Thu tái đầu tư : 80 FVA (7%;5) – 400= 60$
Giá bán trái phiếu vào cuối năm 5: 1009$
Tổng: 1469$
• Lãi suất giảm tạo ra lợi vốn 9$, nhưng lại 
giảm 9$ thu từ tái đầu tư, tổng dòng tiền 
không thay đổi. 
26
Nếu lãi suất tăng lên 9 % trong 5 năm:
Lãi cuống phiếu, 5 80$ = 400$
Thu tái đầu tư : 80 FVA (9%;5) – 400= 78$
Giá bán trái phiếu vào cuối năm 5: 991$
Tổng: 1469$
• Lãi suất tăng đem lại 9$ tăng thêm trong thu 
từ tái đầu tư, bù đắp cho khoản mất vốn 9$, 
tổng dòng tiền không thay đổi. 
27
• Nhận xét
– Định chế tài chính có một khoản nghĩa vụ cố định 
phải thực hiện trong tương lai.
– Thiết lập một danh mục (hay một khoản đầu tư) 
với giá trị bằng PV của khoản nghĩa vụ, và có D 
bằng với thời gian đáo hạn của khoản nghĩa vụ. 
→ khớp vòng đáo hạn bình quân
– Khi lãi suất thay đổi, hai hiệu ứng triệt tiêu nhau, 
loại bỏ rủi ro lãi suất cho khoản nghĩa vụ.
Nghĩa vụ
Giá trị tích lũy của 
khoản đầu tư
D = 5 nămt* t
0
Lãi suất không thay đổi
Lãi suất
tăng
Xây dựng một 
danh mục được “tiêm phòng”
• DA = DL:
– Tính DL
– Tính D của danh mục tài sản DA, bằng bình quân 
gia quyền của D của các tài sản cấu thành danh 
mục.
– Tìm một hỗn hợp tài sản sao cho DA = DL
– Tài trợ đủ cho khoản nghĩa vụ