Bài giảng Đầu tư tài chính - Chương 3: Danh mục rủi ro tối ưu - Phạm Hữu Hồng Thái
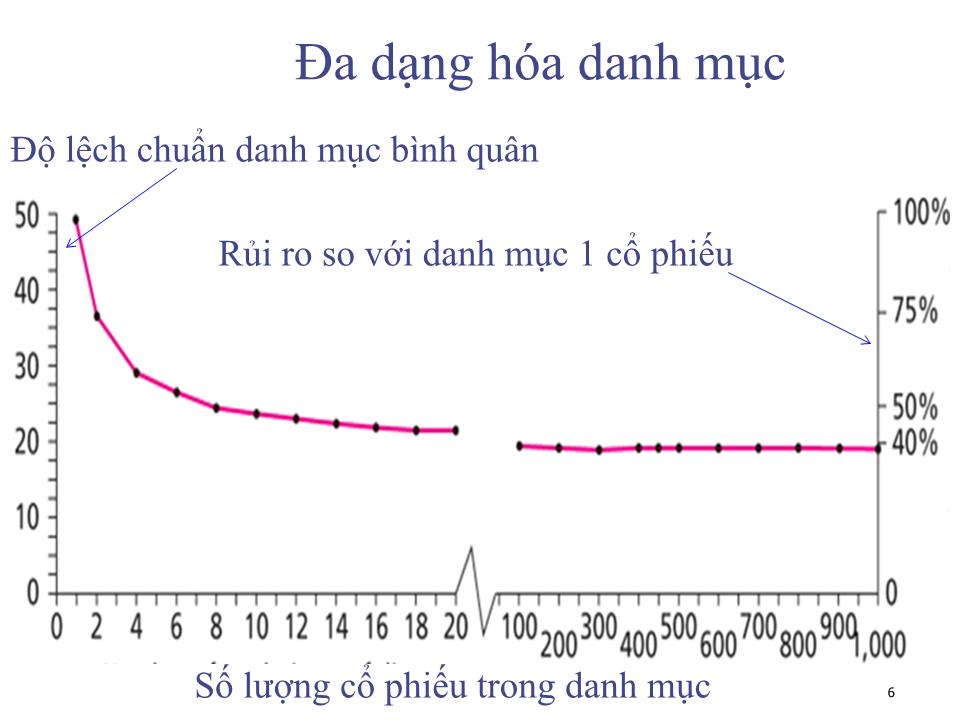
Đa dạng hóa danh mục tài sản rủi ro
Cổ phiếu Vinamilk chịu áp lực từ 2 nguồn rủi ro:
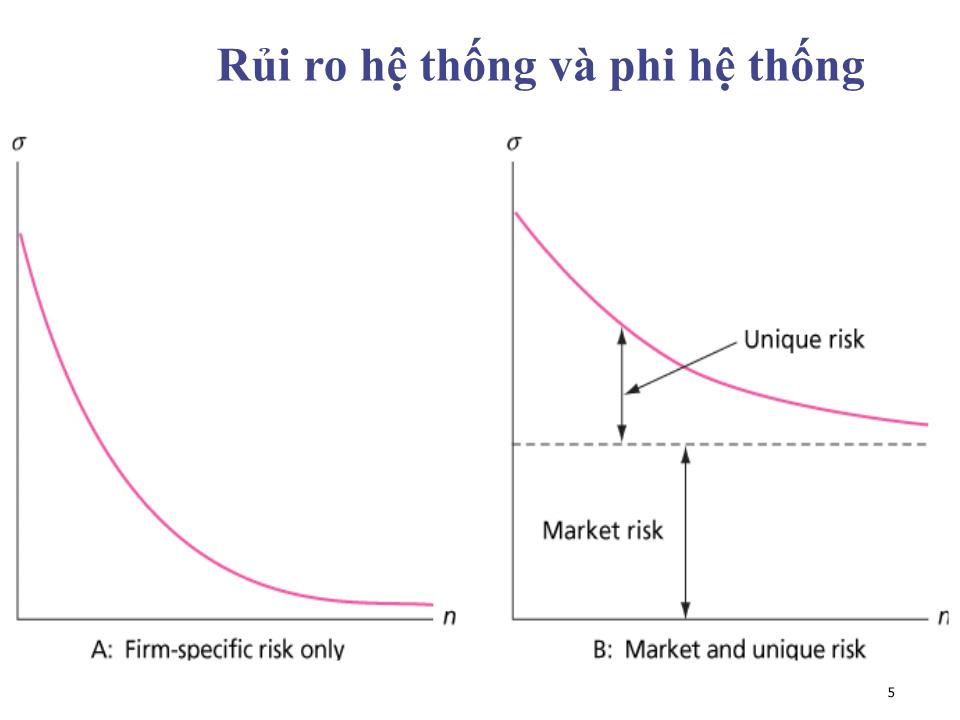
Rủi ro hệ thống: lạm phát, lãi suất, tỷ giá hối đoái, chu kỳ kinh doanh.
Rủi ro phi hệ thống: thay đổi nhân sự, sự thành đạt hay thất bại của công ty
Đa dạng hóa danh mục làm giảm thiểu rủi ro phi hệ thống. Ví dụ, cổ phiếu Vinamilk và ABT
Đa dạng hóa không làm giảm rủi ro hệ thống.
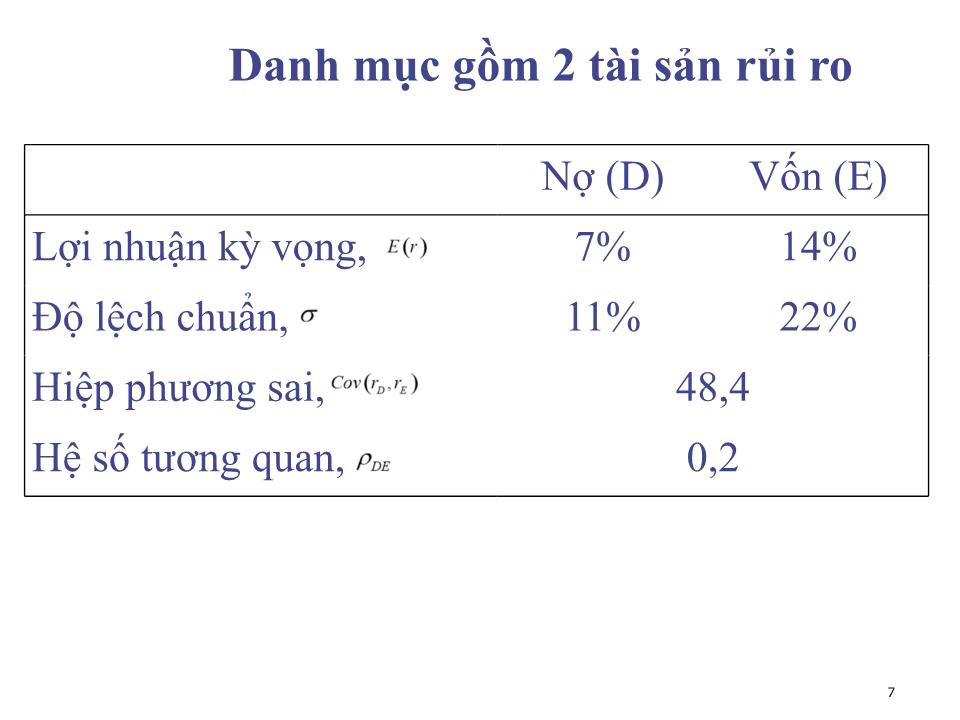
Mô hình lựa chọn danh mục Markowitz
Xây dựng danh mục tối ưu gồm 3 bước:
Bước 1: Xác định mối tương quan giữa lợi nhuận và rủi ro từ tổ hợp cơ hội đầu tư các tài sản rủi ro
Bước 2: Xác định danh mục tài sản rủi ro tối ưu bằng cách tính tỷ lệ đầu tư của mỗi loại tài sản trong danh mục.
Bước 3: Lựa chọn danh mục hoàn thiện bằng cách cân đối giữa danh mục rủi ro tối ưu và tín phiếu kho bạc Nhà nước.

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Đầu tư tài chính - Chương 3: Danh mục rủi ro tối ưu - Phạm Hữu Hồng Thái

1 Lecture 3 DANH MỤC RỦI RO TỐI ƯU (Optimal Risky Portfolios) T.S. Phạm Hữu Hồng Thái TRƯỜNG ĐH TÀI CHÍNH - MARKETING MỤC TIÊU Lecturer 3 Kết thúc Lecture 3, người học có khả năng: Nắm vững chiến lược đa dạng hóa danh mục nhằm giảm thiểu rủi ro; Hiểu một số khái niệm như rủi ro hệ thống và rủi ro phi hệ thống; Xác định lợi nhuận kỳ vọng, độ lệch chuẩn, phương sai, hiệp phương sai, và hệ số tương quan của danh mục 2 tài sản rủi ro; Xác định lợi nhuận kỳ vọng, độ lệch chuẩn, phương sai, hiệp phương sai, và hệ số tương quan của danh mục 2 tài sản rủi ro và 1 tài sản phi rủi ro; Thảo luận mô hình lựa chọn danh mục Markowitz. 2 3 Nội dung Lecture 3 Đa dạng hóa danh mục tài sản rủi ro Danh mục gồm 2 tài sản rủi ro Danh mục gồn 2 tài sản rủi ro và 1 tài sản phi rủi ro Mô hình lựa chọn danh mục Markowitz 4 Đa dạng hóa danh mục tài sản rủi ro Cổ phiếu Vinamilk chịu áp lực từ 2 nguồn rủi ro: Rủi ro hệ thống: lạm phát, lãi suất, tỷ giá hối đoái, chu kỳ kinh doanh. Rủi ro phi hệ thống: thay đổi nhân sự, sự thành đạt hay thất bại của công ty Đa dạng hóa danh mục làm giảm thiểu rủi ro phi hệ thống. Ví dụ, cổ phiếu Vinamilk và ABT Đa dạng hóa không làm giảm rủi ro hệ thống. 5 Rủi ro hệ thống và phi hệ thống Đa dạng hóa danh mục 6 Độ lệch chuẩn danh mục bình quân Số lượng cổ phiếu trong danh mục Rủi ro so với danh mục 1 cổ phiếu 7 Danh mục gồm 2 tài sản rủi ro Nợ (D) Vốn (E) Lợi nhuận kỳ vọng, 7% 14% Độ lệch chuẩn, 11% 22% Hiệp phương sai, 48,4 Hệ số tương quan, 0,2 8 Lợi nhuận của danh mục: Lợi nhuận kỳ vọng của danh mục: Phương sai của danh mục: Danh mục gồm 2 tài sản rủi ro 9 Định nghĩa theo cách khác: Phương sai của danh mục là tổng các hiệp phương sai có trọng số, và mỗi tỷ trọng là tích các tỷ trọng danh mục của các cặp tài sản trong biểu thức hiệp phương sai. Danh mục gồm 2 tài sản rủi ro 10 Hiệp phương sai của một biến với chính nó được định nghĩa như là phương sai của biến đó. Danh mục gồm 2 tài sản rủi ro 11 MA TRẬN HIỆP PHƯƠNG SAI ĐƠN BIÊN Tỷ trọng danh mục Danh mục gồm 2 tài sản rủi ro 12 Danh mục gồm 2 tài sản rủi ro MA TRẬN HIỆP PHƯƠNG SAI ĐA BIÊN Tỷ trọng danh mục Phương sai DM 13 Chứng minh: Ta có: Hay: Ví dụ 7.1: 14 b) Chứng minh: phương sai của danh mục là: Ta có: Ma trận hiệp phương sai đơn biên: Ví dụ 7.1: 15 Có 9 biểu thức trong ma trận hiệp phương sai và phương sai của danh mục từ 9 biểu thức này là: Ví dụ 7.1: 16 giảm khi Nếu , vẫn nhỏ hơn và Ta có: Hay: Hệ số tương quan (Correlation coefficient) 17 Hệ số tương quan dao động trong khoảng [-1, 1] , 2 chứng không tương quan. Hệ số tương quan (Correlation coefficient) 18 , 2 chứng khoán di chuyển ngược chiều nhau. Hệ số tương quan (Correlation coefficient) 19 , 2 chứng khoán di chuyển cùng chiều nhau. Hệ số tương quan (Correlation coefficient) 20 Khi : Hay: Khi Và = giá trị tuyệt đối , và nhà đầu tư thiết lập vị thế hoàn hảo , nghĩa là: Hệ số tương quan (Correlation coefficient) 21 Tỷ lệ danh mục tối ưu (rủi ro danh mục bị triệt tiêu) Hệ số tương quan (Correlation coefficient) 22 Lợi nhuận kỳ vọng của DM gồm TP & CP: Phương sai của danh mục: Độ lệch chuẩn: Ví dụ 7.2 23 Lợi nhuận danh mục là hàm số của tỷ trọng đầu tư Lợi nhuận kỳ vọng 7% 14% 0 1.0 Qũy cổ phiếu Qũy trái phiếu 2.0 0 1.0 1.5 -1.0 -0,5 W (cổ phiếu) W (trái phiếu) = 1 – W (cp) 24 Nếu W D thay đổi từ 0-1 (W E thay đổi từ 1-0), lợi nhuận danh mục giảm từ 14%-7%. Nếu W D >1 (1,5) và W E lợi nhuận kỳ vọng của DM giảm đáng kể (từ 7% xuống còn 3,5%). Nếu W D 1 (1,5), bán khống trái phiếu. Ví dụ 7.2 25 Lợi nhuận kỳ vọng và độ lệch chuẩn có hệ số tương quan thay đổi Độ lệch chuẩn danh mục với hệ số tương quan cho trước 0,00 1,00 14,00 22,00 22,00 22,00 22,00 0,10 0,90 13,30 18,70 19,83 20,05 20,90 0,20 0,80 12,60 15,40 17,74 18,17 19,80 0,30 0,70 11,90 12,10 15,75 16,38 18,70 0,40 0,60 11,20 8,80 13,91 14,73 17,60 0,50 0,50 10,50 5,50 12,30 13,25 16,50 0,60 0,40 9,80 2,20 11,00 12,01 15,40 0,70 0,30 9,10 1,10 10,14 11,10 14,30 0,80 0,20 8,40 4,40 9,84 10,60 13,20 0,90 0,10 7,70 7,70 10,14 10,56 12,10 1,00 0,00 7,00 11,00 11,00 11,00 11,00 Danh mục phương sai nhỏ nhất 0,67 0,8 0,86 0,33 0,2 0,14 9,31 8,4 7,98 0,11 9,84 10,52 26 Độ lệch chuẩn danh mục là hàm số tỷ trọng 5 10 15 20 25 30 1,1 0,5 0 1,0 1,5 -0,5 0,3 Độ lệch chuẩn danh mục Tỷ trọng đầu tư cổ phiếu 27 Tỷ trọng có phương sai nhỏ nhất 28 Lợi nhuận kỳ vọng là hàm số của độ lệch chuẩn 0 2 4 6 8 10 12 14 16 18 20 22 5 6 7 8 9 10 11 12 13 14 E Lợi nhuận kỳ vọng D Độ lệch chuẩn 29 Với thông số sau, hãy xác định tổ hợp cơ hội đầu tư gồm quỹ trái phiếu và cổ phiếu: Ví dụ 7.3 Nợ (D) Vốn (E) 8% 13% 12% 20% 0,25 30 Ma trận hiệp phương sai đơn biên: Danh mục có phương sai nhỏ nhất: Ví dụ 7.3 Quỹ D E D 144 60 E 60 400 31 Lợi nhuận kỳ vọng và độ lệch chuẩn danh mục có phương sai nhỏ nhất: Ví dụ 7.3 32 Lợi nhuận kỳ vọng và độ lệch chuẩn theo các tỷ trọng khác nhau 0,0 1,0 8,0 12,00 0,1 0,9 8,5 11,46 0,2 0,8 9,0 11,29 0,3 0,7 9,5 11,48 0,4 0,6 10,0 12,03 0,5 0,5 10,5 12,88 0,6 0,4 11,0 13,99 0,7 0,3 11,5 15,30 0,8 0,2 12,0 16,76 0,9 0,1 12,5 18,34 1,0 0,0 13,0 20,00 0,1981 0,8019 8,99 11,29 Danh mục phương sai nhỏ nhất 33 Xem xét 1 danh mục gồm 2 quỹ đầu tư: cổ phiếu và trái phiếu (tài sản phi rủi ro, r f = 5%) Sử dụng thông tin từ Bảng 7.1 để phân tích biểu đồ. Có 2 đường CAL A và CAL B Danh mục A: Phương sai nhỏ nhất 14% (cổ phiếu), 86% (trái phiếu), E(r A ) = 7,98%, SD A = 10,52% Danh mục gồm tài sản rủi ro và phi rủi ro 34 Danh mục B: 30% (cổ phiếu), 70% (trái phiếu), E(r B ) = 9,10%, SD B = 11,10% SB > SA => B thống trị A Danh mục gồm tài sản rủi ro và phi rủi ro 35 Tổ hợp các cơ hội đầu tư 0 5 10 15 20 25 5 6 7 8 9 10 11 12 13 D B A 14 E Lợi nhuận kỳ vọng, % Độ lệch chuẩn, % CAL(A) CAL(B) Dịch chuyển A lên trên tiếp cận với đường cong tổ hợp các cơ hội đầu tư. CAL(p) có hệ số gốc cao nhất Danh mục tiệm cận p là danh mục tối ưu . 36 Danh mục gồm tài sản rủi ro và phi rủi ro 37 Danh mục gồm tài sản rủi ro và phi rủi ro D E P 0 5 10 15 20 25 2 4 7 8 10 11 12 13 Lợi nhuận kỳ vọng, % Độ lệch chuẩn, % 9 Tổ hợp cơ hội đầu tư của các tài sản rủi ro CAL(P) 15,53 11,55 Cần xác định W E và W D để có danh mục tối ưu. Độ dốc đường phân phối vốn tiệm cận Lợi nhuận và độ lệch chuẩn: 38 Danh mục gồm tài sản rủi ro và phi rủi ro 39 Tối đa hóa độ dốc phải thỏa điều kiện: Thay thế: , , và vào phương trình trên. Lấy đạo hàm và cho = 0, ta có: Danh mục gồm tài sản rủi ro và phi rủi ro 40 Sử dụng thông tin từ Bảng 7.1, ta có Lợi nhuận kỳ vọng & độ lệch chuẩn: Ví dụ 7.4: Danh mục rủi ro tối ưu 41 CAL tối ưu có hệ số gốc cực đại: Với A = 4, 67,89% (tài sản rủi ro) và 32,11% (tài sản phi rủi ro) Ví dụ 7.4: Danh mục rủi ro tối ưu 42 65% (cổ phiếu) và 35% (trái phiếu), nghĩa là: Quỹ TP: Quỹ cổ phiếu: Tỷ trọng danh mục hoàn thiện: Quỹ trái phiếu: 23,76% Quỹ cổ phiếu: 44,13% Tín phiếu KBNN: 32,11% Tổng: 100% Ví dụ 7.4: Danh mục rủi ro tối ưu Lợi nhuận kỳ vọng & độ lệch chuẩn danh mục hoàn thiện: 43 Ví dụ 7.4: Danh mục rủi ro tối ưu 44 Hình7.8: Danh mục hoàn thiện tối ưu C D E P 0 5 10 15 20 25 2 4 7 8 10 11 12 13 Lợi nhuận kỳ vọng, % Độ lệch chuẩn, % 9 Danh mục hoàn thiện tối ưu CAL(P) 15,53 11,55 Tổ hợp cơ hội đầu tư tài sản rủi ro Đường cong bàng quan r f = 5% Danh mục rủi ro tối ưu 45 Quỹ Dragon Capital gồm 2 loại CP X và Y và tín phiếu KBNN. Hệ số tương quan X và Y là -0,2 Ví dụ 7.5: Lợi nhuận kỳ vọng Độ lệch chuẩn X 10% 20% Y 30% 60% Tín phiếu kho bạc NN 5% 0% 46 a) Vẽ tổ hợp cơ hội đầu tư của 2 quỹ X và Y: Tỷ trọng DM có phương sai nhỏ nhất: Ví dụ 7.5: Quỹ X Y X 400 -240 Y -240 3600 47 Lợi nhuận kỳ vọng & độ lệch chuẩn danh mục có phương sai nhỏ nhất: Ví dụ 7.5: 48 Lợi nhuận & độ lệch chuẩn danh mục theo các tỷ trọng đầu tư khác nhau 0,0 1,0 30.00 60.00 0,1 0,9 28.00 53.64 0,2 0,8 26.00 47.36 0,3 0,7 24.00 41.22 0,4 0,6 22.00 35.28 0,5 0,5 20.00 29.66 0,6 0,4 18.00 24.59 0,7 0,3 16.00 20.47 0,8 0,2 14.00 17.98 0,9 0,1 12.00 17.80 1,0 0,0 10.00 20.00 0,8571 0,1429 12.86 17.57 Danh mục có phương sai nhỏ nhất 49 b) Danh mục rủi ro tối ưu Tỷ lệ đầu tư vào tài sản rủi ro: Lợi nhuận kỳ vọng & độ lệch chuẩn DMTƯ: Ví dụ 7.5: 50 Danh mục p không phải là DM có phương sai nhỏ nhất. Với W X = 85,71% và W Y = 14,29%, lợi nhuận kỳ vọng và độ lệch chuẩn của DM có phương sai nhỏ nhất là: E(r) =12,86% và SD = 17,57%. SD (DM tối ưu) > SD (DM có phương sai nhỏ nhất) c) Hệ số gốc của CAL tối ưu: Ví dụ 7.5: 51 d) Tỷ lệ đầu tư vào danh mục hoàn thiện: Với A = 5, Cổ phiếu X: 0,5089 × 68,18 = 34,70% Cổ phiếu Y: 0,5089 × 31,82 = 16,19% Tín phiếu KBNN 1 – 0,5089 = 0,4911 hay 49,11% Ví dụ 7.5: 52 Xây dựng danh mục tối ưu gồm 3 bước: Bước 1 : Xác định mối tương quan giữa lợi nhuận và rủi ro từ tổ hợp cơ hội đầu tư các tài sản rủi ro Bước 2 : Xác định danh mục tài sản rủi ro tối ưu bằng cách tính tỷ lệ đầu tư của mỗi loại tài sản trong danh mục. Bước 3 : Lựa chọn danh mục hoàn thiện bằng cách cân đối giữa danh mục rủi ro tối ưu và tín phiếu kho bạc Nhà nước. Mô hình lựa chọn danh mục Markowitz 53 Xác định cơ hội đầu tư : Xác định đường biên giới hạn có phương sai nhỏ nhất của tài sản rủi ro. Đường biên giới hạn: Đồ thị thể hiện phương sai nhỏ nhất có thể đạt được ứng với một tỷ suất lợi nhuận cho trước của danh mục. Với lợi nhuận kỳ vọng, phương sai, và hiệp phương sai cho trước, có thể xác định danh mục có phương sai nhỏ nhất ứng với lợi nhuận kỳ vọng mục tiêu. Mô hình lựa chọn danh mục Markowitz 54 Đường biên giới hạn hiệu quả Mỗi loại tài sản Đường biên giới hạn phương sai nhỏ nhất Danh mục phương sai nhỏ nhất Đường biên giới hạn hiệu quả E(r) 55 Đường biên giới hạn hiệu quả & đường phân phối vốn tối ưu Đ ườ ng giới hạn biên hiệu quả CAL(p) p r f E(r) 56 Có n chứng khoán sẽ có n ước lượng điểm của lợi nhuận kỳ vọng n × n ước lượng của ma trận hiệp phương sai Trong đó: n các yếu tố theo đường chéo là ước lượng của phương sai các yếu tố không thuộc đường chéo là ước lượng của hiệp phương sai Công thức tổng quát 57 Ví dụ: Danh mục có 50 chứng khoán, có 50 ước lượng lợi nhuận kỳ vọng, 50 ước lượng phương sai, 1.225 ước lượng hiệp phương sai. Lợi nhuận kỳ vọng và phương sai của danh mục (công thức tổng quát): Công thức tổng quát 58 ÔN TẬP Nêu chiến lược đa dạng hóa danh mục? Nêu rủi ro hệ thống và phi hệ thống? Nêu công thức xác định lợi nhuận kỳ vọng, độ lệch chuẩn, phương sai, hiệp phương sai, và hệ số tương quan của danh mục 2 tài sản rủi ro? Nêu công thức xác định lợi nhuận kỳ vọng, độ lệch chuẩn, phương sai, hiệp phương sai, và hệ số tương quan của danh mục 2 tài sản rủi ro và 1 tài sản phi rủi ro. Nêu các bước xây dựng mô hình lựa chọn danh mục Markowitz.
File đính kèm:
 bai_giang_dau_tu_tai_chinh_chuong_3_danh_muc_rui_ro_toi_uu_p.ppt
bai_giang_dau_tu_tai_chinh_chuong_3_danh_muc_rui_ro_toi_uu_p.ppt

