Bài giảng Đầu tư tài chính - Chương 2: Độ E ngại rủi ro và chiến lược phân phối tài sản - Phạm Hữu Hồng Thái
Phần bù rủi ro (rM)
Là sự khác biệt giữa lợi nhuận kỳ vọng và lãi suất phi rủi ro
Lãi suất phi rủi ro là lãi suất mà nhà đầu tư được hưởng khi đầu tư vào các loại tài sản phi rủi ro
Cổ phiếu thường được xem như tài sản có rủi ro cao. Ví dụ: E(r) = 14%, rf = 5% => rM= 9%
Lợi nhuận tài sản rủi ro được xác định cuối kỳ. Dùng lợi nhuận vượt mức (excess return) để xác định phần bù rủi ro.
Tỷ suất lợi nhuận tương đương bền vững-CER
CER là mức tỷ suất tại đó điểm hữu dụng của cả 2 danh mục rủi ro và phi rủi ro bằng nhau
CER luôn thấp hơn lợi nhuận của danh mục phi rủi ro cho tất cả các nhà đầu tư e ngại rủi ro.
CER là lợi nhuận kỳ vọng của danh mục rủi ro đối với nhà đầu tư trung tính (Risk neutral).
CER luôn cao hơn lợi nhuận của danh mục phi rủi ro cho tất cả các nhà đầu tư thích rủi ro.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
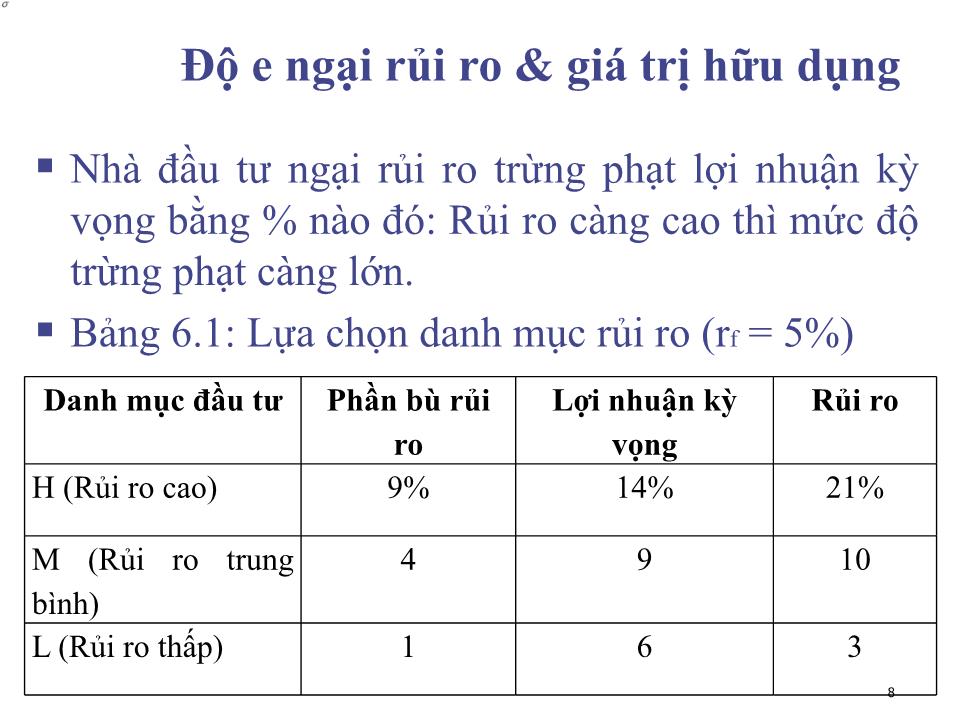
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Đầu tư tài chính - Chương 2: Độ E ngại rủi ro và chiến lược phân phối tài sản - Phạm Hữu Hồng Thái

1 CHƯƠNG 2 ĐỘ E NGẠI RỦI RO & CHIẾN LƯỢC PHÂN PHỐI TÀI SẢN T.S. Phạm Hữu Hồng Thái TRƯỜNG ĐH TÀI CHÍNH - MARKETING MỤC TIÊU CHƯƠNG 2 Kết thúc Chương 2, người học có khả năng: Nắm vững các khái niệm cơ bản về lý thuyết danh mục như phần bù rủi ro (Risk premiums), độ e ngại rủi ro (Risk aversion), và giá trị hữu dụng; Xác định hàm hữu dụng (Utility function) và đường cong bàng quan (Indifference curve) trong đầu tư; Phân tích danh mục bao gồm tài sản rủi ro và phi rủi ro, và xây dựng đường phân phối vốn (Capital Allocation Line – CAL); So sánh chiến lược chủ động và chiến lược thụ động; Xác định đường thị trường vốn (Capital Market Line). 2 3 Nội dung chương 2 Phần bù rủi ro Độ e ngại rủi ro Độ e ngại rủi ro & giá trị hữu dụng Phân phối vốn vào tài sản rủi ro và phi rủi ro Chấp nhận rủi ro và phân phối tài sản Chiến lược thụ động: Đường thị trường vốn 4 Phần bù rủi ro (r M ) Là sự khác biệt giữa lợi nhuận kỳ vọng và lãi suất phi rủi ro Lãi suất phi rủi ro là lãi suất mà nhà đầu tư được hưởng khi đầu tư vào các loại tài sản phi rủi ro Cổ phiếu thường được xem như tài sản có rủi ro cao. Ví dụ: E (r) = 14%, r f = 5% => r M = 9% Lợi nhuận tài sản rủi ro được xác định cuối kỳ. Dùng lợi nhuận vượt mức (excess return) để xác định phần bù rủi ro. 5 Độ e ngại rủi ro Cổ phiếu trở nên kém hấp dẫn khi r M =0 và độ e ngại rủi ro cao. Giả sử danh mục được lựa chọn dựa trên lợi nhuận kỳ vọng và phương sai , phần bù rủi ro sẽ là: Phần bù rủi ro sẽ phụ thuộc vào 2 yếu tố: Độ e ngại rủi ro A và rủi ro danh mục 6 Độ e ngại rủi ro Xác định độ e ngại rủi ro theo danh mục thị trường: Phần bù rủi ro càng cao thì độ e ngại của nhà đầu tư rất lớn. Hai phương trình trên đều chỉ áp dụng duy nhất cho phương sai của danh mục thị trường. Độ e ngại rủi ro của nhà đầu tư nằm trong khoảng từ 2 – 4 7 Ví dụ 6.1: Độ e ngại rủi ro Lợi nhuận của danh mục thị trường S&P500 vào năm tới khoảng 10% Độ lệch chuẩn của lợi nhuận là 18% Độ e ngại rủi ro bình quân của các nhà đầu tư? 8 Độ e ngại rủi ro & giá trị hữu dụng Nhà đầu tư ngại rủi ro trừng phạt lợi nhuận kỳ vọng bằng % nào đó: Rủi ro càng cao thì mức độ trừng phạt càng lớn. Bảng 6.1: Lựa chọn danh mục rủi ro (r f = 5%) Danh mục đầu tư Phần bù rủi ro Lợi nhuận kỳ vọng Rủi ro H (Rủi ro cao) 9% 14% 21% M (Rủi ro trung bình) 4 9 10 L (Rủi ro thấp) 1 6 3 9 Hàm số cho điểm hữu dụng Khó xác định được danh mục nào hấp dẫn hơn do rủi ro tăng theo lợi nhuận. Mỗi nhà đầu tư đều có thể chỉ ra một điểm hữu dụng cho mỗi danh mục. Danh mục với điểm hữu dụng cao sẽ có lợi nhuận kỳ vọng cao và ngược lại. Hàm số cho điểm hữu dụng của danh mục: 10 Ví dụ 6.2: Sử dụng hệ thống cho điểm hữu dụng để đánh giá danh mục Gỉa sử, chúng ta đang xem xét 3 nhà đầu tư với 3 cấp độ e ngại rủi ro khác nhau: A 1 = 2,5; A 2 = 3; và A 3 = 4,5 , tương ứng với 3 danh mục trong Bảng 6.1. Bởi vì, lãi suất phi rủi ro là 5% nên tất cả 3 nhà đầu tư sẽ chọn điểm hữu dụng (0,05) cho danh mục phi rủi ro. 11 Bảng 6.2: Điểm hữu dụng của 3 danh mục cho 3 nhà đầu tư có 3 cấp độ e ngại rủi ro Độ e ngại rủi ro (A) Điểm hữu dụng của danh mục L Điểm hữu dụng của danh mục M Điểm hữu dụng của danh mục H 2,5 3 4,5 12 Ví dụ 6.3: Một danh mục đầu tư có lợi nhuận kỳ vọng 20% và độ lệch chuẩn 30%. Lợi nhuận phi rủi ro được cho là 7%. Câu hỏi đặt ra là liệu nhà đầu tư với độ e ngại rủi ro A = 4 thích đầu tư vào tín phiếu kho bạc hay danh mục rủi ro này? Hãy xem xét trong trường hợp A = 2. 13 Ví dụ 6.3: A = 4, giá trị hữu dụng của danh mục rủi ro là: Trong khi đó, giá trị hữu dụng của tín phiếu là: A = 2, Lợi nhuận tín phiếu kho bạc vẫn 0,07. Nhà đầu tư ít ngại rủi ro sẽ thích đầu tư vào danh mục có rủi ro cao hơn. 14 Tỷ suất lợi nhuận tương đương bền vững-CER CER là mức tỷ suất tại đó điểm hữu dụng của cả 2 danh mục rủi ro và phi rủi ro bằng nhau CER luôn thấp hơn lợi nhuận của danh mục phi rủi ro cho tất cả các nhà đầu tư e ngại rủi ro. CER là lợi nhuận kỳ vọng của danh mục rủi ro đối với nhà đầu tư trung tính (Risk neutral). CER luôn cao hơn lợi nhuận của danh mục phi rủi ro cho tất cả các nhà đầu tư thích rủi ro. Sự đánh đổi giữa lợi nhuận và rủi ro của danh mục tiềm năng, P. 15 I II III IV Tây Bắc (hướng lựa chọn) p E(r) 16 Đường cong bàng quan-Indifference Curve p Đường cong bàng quan Q E(r) 17 Gía trị hữu dụng của danh mục, A = 4 Lợi nhuận kỳ vọng, Độ lệch chuẩn, 0,1 0,200 0,15 0,255 0,2 0,300 0,25 0,339 18 Ví dụ 6.4 E(r) Ngại rủi ro hơn (more risk-averse) Ít ngại rủi ro hơn (less risk-averse) p 19 Ví dụ: Lượng hóa độ e ngại rủi ro Phân phối xác suất lợi nhuận được mô tả trong biểu đồ sau: r (lỗ) = -1 (-100%) r (không lỗ) = 0 1-p p 20 Ví dụ: Lượng hóa độ e ngại rủi ro Độ lệch từ lợi nhuận kỳ vọng, -1-(-p) = p-1 0 – (-p) = p 1-p p 21 Ví dụ: Lượng hóa độ e ngại rủi ro Giá trị hữu dụng của nhà đầu tư trong trường hợp có bảo hiểm. Cân bằng phương trình hữu dụng của tài sản có đảm bảo và phương trình hữu dụng của tài sản không đảm bảo: Hoặc, mức phí bảo hiểm tối đa là: 22 Hệ số ngại rủi ro (A) Lỗ ước tính, p = 0,0001 Lỗ ước tính, p = 0,01 Phí bảo hiểm tối đa, v, như là số nhân của lỗ ước tính, p Phí bảo hiểm tối đa, v, như là số nhân của lỗ ước tính, p 0 1,0000 1,0000 1 1,5000 1,4950 2 1,9999 1,9900 3 2,4999 2,4850 4 2,9998 2,9800 5 3,4998 3,4750 Mối quan hệ giữa độ e ngại rủi ro và chi phí bảo hiểm 23 Phân phối vốn vào tài sản rủi ro và tài sản phi rủi ro Lựa chọn tỷ lệ phần trăm để đầu tư vào tài sản rủi ro và phi rủi ro. Cổ phiếu blue chips: Trái phiếu dài hạn: Tỷ trọng của danh mục rủi ro p và tài sản phi rủi ro trong danh mục hoàn thiện (complete portfolio) Tài sản rủi ro Tài sản phi rủi ro 24 Phân phối vốn vào tài sản rủi ro và tài sản phi rủi ro Tỷ trọng của mỗi loại tài sản trong danh mục hoàn thiện là: CP blue chips TP dài hạn Danh mục rủi ro = 0,6 25 Danh mục gồm 1 tài sản rủi ro và 1 tài sản phi rủi ro Lợi nhuận kỳ vọng của danh mục hoàn thiện, C. Lợi nhuận của danh mục hoàn thiện phụ thuộc vào cả phần bù rủi ro của danh mục rủi ro và vị thế của nhà đầu tư trong tài sản đó. Độ lệch chuẩn của danh mục hoàn thiện: 26 Đường phân phối vốn – Capital Allocation Line (CAL) P CAL = Đường phân phối vốn F Q 27 Hệ số gốc (Sharp ratio) của đường thị trường vốn Hệ số gốc S của đường phân phối vốn là tỷ số giữa phần bù rủi ro và độ lệch chuẩn của danh mục rủi ro. Tỷ số lợi nhuận-rủi ro (reward-to-variability ratio). 28 Hệ số Sharp có khác với hệ số đối với danh mục chỉ bao gồm một loại tài sản rủi ro? 29 Hệ số gốc đồng nhất Hệ số gốc của tất cả các danh mục nằm trên đường phân phối vốn đều như nhau. Giả sử chúng ta xây dựng một danh mục với tỷ lệ 50% tài sản rủi ro và 50% tài sản phi rủi ro. 30 Đường phân phối vốn – lãi suất vay và cho vay P CAL 31 Ví dụ 6.7: Hệ số đòn bẩy tài chính Vị thế đòn bẩy của tài sản rủi ro được xác định như sau: Danh mục có hệ số đòn bẩy (leveraged portfolio) sẽ có rủi ro cao hơn danh mục không có hệ số đòn bẩy (Vị thế đoản) 32 Chấp nhận rủi ro & phân phối tài sản Đường phân phối vốn đã cung cấp cho nhà đầu tư nhiều sự lựa chọn (Cho vay với lãi suất phi rủi ro) (Đi vay với lãi suất phi rủi ro) Lợi nhuận & phương sai của danh mục hoàn thiện, C 33 Chấp nhận rủi ro & phân phối tài sản Nhà đầu tư cố gắng tối đa hóa giá trị hữu dụng bằng cách chọn tỷ lệ phân phối ( W p ) vốn tốt nhất vào tài sản rủi ro. Lợi nhuận kỳ vọng tăng nhưng độ lệch chuẩn của danh mục cũng tăng. Tuy nhiên, giá trị hữu dụng có thể tăng hoặc giảm còn tùy thuộc vào độ e ngại rủi ro của nhà đầu tư Mối quan hệ giữa độ hữu dụng (U) và tỷ trọng , A = 4 34 (1) (2) (3) (4) 0 0.050 0.000 0.0500 0,1 0.062 0.025 0.0608 0,2 0.074 0.050 0.0690 0,3 0.086 0.075 0.0748 0,4 0.098 0.100 0.0780 0,5 0.110 0.125 0.0788 0,6 0.122 0.150 0.0770 0,7 0.134 0.175 0.0728 0,8 0.146 0.200 0.0660 0,9 0.158 0.225 0.0568 1.0 0.170 0.250 0.0450 Gía trị hữu dụng như là hàm số phân phối tài sản rủi ro, 35 0,2 0,4 0,6 0,8 1 1,2 0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 Hữu dụng Phân phối tài sản rủi ro , 0,48 0,0788 Tối đa hóa giá trị hữu dụng của nhà đầu tư. Lấy đạo hàm 2 vế và cho bằng 0, chúng ta sẽ xác định được giá trị tối ưu, , cho nhà đầu tư ngại rủi ro khi đầu tư vào tài sản rủi ro. 36 37 Ví dụ 6.8: Phân phối vốn Với r f = 5%, E(r p ) = 17%, , hãy xác định tỷ lệ tối ưu cho nhà đầu tư có độ e ngại rủi ro A = 4. Dùng 48% từ nguồn vốn tự có để đầu tư vào tài sản rủi ro và 52% đầu tư vào tài sản phi rủi ro. Với 48% đầu tư vào danh mục tài sản rủi ro, lợi nhuận kỳ vọng và độ lệch chuẩn của danh mục hoàn thiện là: 38 Ví dụ 6.8: Phân phối vốn Phần bù rủi ro của danh mục hoàn thiện là: Đây là phần bù mà nhà đầu tư được thụ hưởng khi đầu tư vào danh mục tài sản rủi ro có độ lệch chuẩn 12%. 39 Xác định đường cong bàng quan Xây dựng các đường cong bàng quan để đưa ra quyết định tỷ lệ tài sản tối ưu trong danh mục. A =1, danh mục gồm 1 tài sản phi rủi ro, r f = 6% Duy trì U = 0,06 khi đầu tư vào tài sản rủi ro 40 Xác định đường cong bàng quan Với , Với , Vẽ đồ thị của tổ hợp này sẽ tạo ra các đường cong bàng quan. 41 Dữ liệu thiết lập đường cong bàng quan, A = 1, 3. A = 1 A = 3 U = 0,06 U = 0,08 U = 0,06 U = 0,08 0 0.0600 0.0800 0.0600 0.0800 0,05 0.0613 0.0813 0.0638 0.0838 0,10 0.0650 0.0850 0.0750 0.0950 0,15 0.0713 0.0913 0.0938 0.1138 0,20 0.0800 0.1000 0.1200 0.1400 0,25 0.0913 0.1113 0.1538 0.1738 0,30 0.1050 0.1250 0.1950 0.2150 0,35 0.1213 0.1413 0.2438 0.2638 0,40 0.1400 0.1600 0.3000 0.3200 0,45 0.1613 0.1813 0.3638 0.3838 0,50 0.1850 0.2050 0.4350 0.4550 42 Đường cong bàng quan (U =0,06 và 0,08 (A = 1, 3) U = 0,08 U = 0,06 0,1 0,2 0,3 0,4 0,5 43 Danh mục hoàn thiện tối ưu sử dụng tổ hợp đường cong bàng quan Với , giá trị hữu dụng đạt cực đại và lợi nhuận kỳ vọng và độ lệch chuẩn của danh mục hoàn thiện là: và Giá trị hữu dụng cực đại với A = 4 Sử dụng phương trình để xác định đường cong bàng quan Sử dụng để xác định lợi nhuận kỳ vọng trên đường CAL. Lợi nhuận kỳ vọng trên 4 đường bàng quan và CAL 44 U = 0,05 U = 0,0654 U = 0,0788 U = 0,0842 CAL 0,00 0.0500 0.0654 0.0788 0.0842 0.0500 0,02 0.0508 0.0662 0.0796 0.0850 0.0596 0,04 0.0532 0.0686 0.0820 0.0874 0.0692 0,06 0.0572 0.0726 0.0860 0.0914 0.0788 0,08 0.0628 0.0782 0.0916 0.0970 0.0884 0,10 0.0700 0.0854 0.0988 0.1042 0.0980 0,12 0.0788 0.0942 0.1076 0.1130 0.1076 0,14 0.0892 0.1046 0.1180 0.1234 0.1172 0,16 0.1012 0.1166 0.1300 0.1354 0.1268 0,18 0.1148 0.1302 0.1436 0.1490 0.1364 0,20 0.1300 0.1454 0.1588 0.1642 0.1460 0,22 0.1468 0.1622 0.1756 0.1810 0.1556 0,24 0.1652 0.1806 0.1940 0.1994 0.1652 0,26 0.1852 0.2006 0.2140 0.2194 0.1748 0,28 0.2068 0.2222 0.2356 0.2410 0.1844 0,30 0.2300 0.2454 0.2588 0.2642 0.1940 xác định danh mục hoàn thiện tối ưu 45 C P 46 Ví dụ 6.9 : p 47 ÔN TẬP Phần bù rủi ro, độ e ngại rủi ro, giá trị hữu dụng? Hàm hữu dụng và đường cong bàng quan? Danh mục gồm tài sản rủi ro và phi rủi ro, và xây dựng đường phân phối vốn? Chiến lược chủ động và thụ động? Đường thị trường vốn?
File đính kèm:
 bai_giang_dau_tu_tai_chinh_chuong_2_do_e_ngai_rui_ro_va_chie.ppt
bai_giang_dau_tu_tai_chinh_chuong_2_do_e_ngai_rui_ro_va_chie.ppt

