Bài giảng Cơ sở kỹ thuật robot - Chương 3: Các phép biến đổi tọa độ
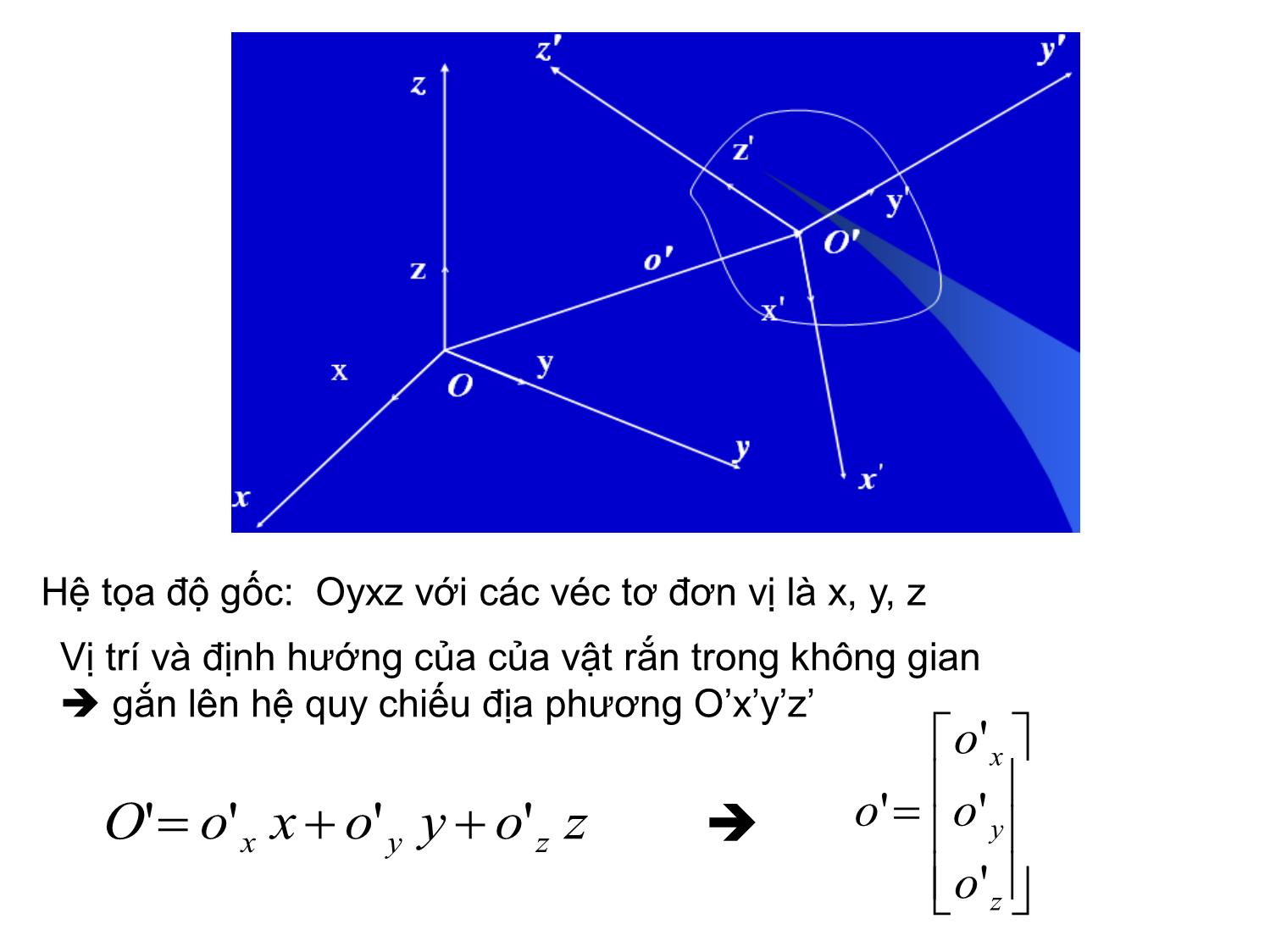
Hệ tọa độ gốc: Oyxz với các véc tơ đơn vị là x, y, z
Vị trí và định hướng của của vật rắn trong không gian
gắn lên hệ quy chiếu địa phương O’x’y’z’
Hướng của vật <== các
véc tơ đơn vị x’, y’, z’:
Các thành phần của các véc tơ đơn vị (x’x, x’y, x’z) là cosin chỉ
phương của các trục của hệ tọa độ địa phương so với hệ quy
chiếu chung.
X’
x = X’.cos(X’,X),

Trang 1
Trang 2
Trang 3
Trang 4
Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cơ sở kỹ thuật robot - Chương 3: Các phép biến đổi tọa độ", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cơ sở kỹ thuật robot - Chương 3: Các phép biến đổi tọa độ

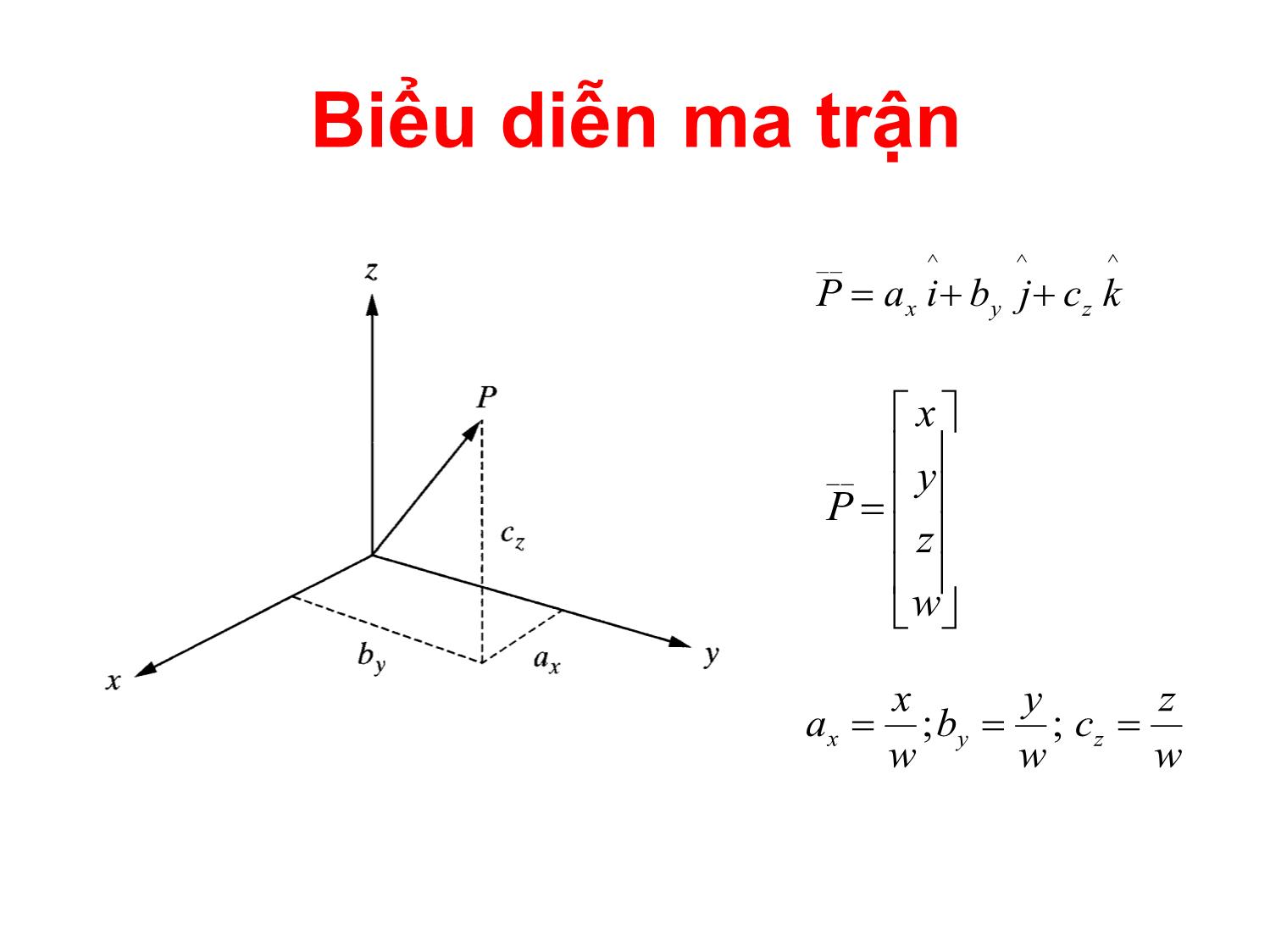
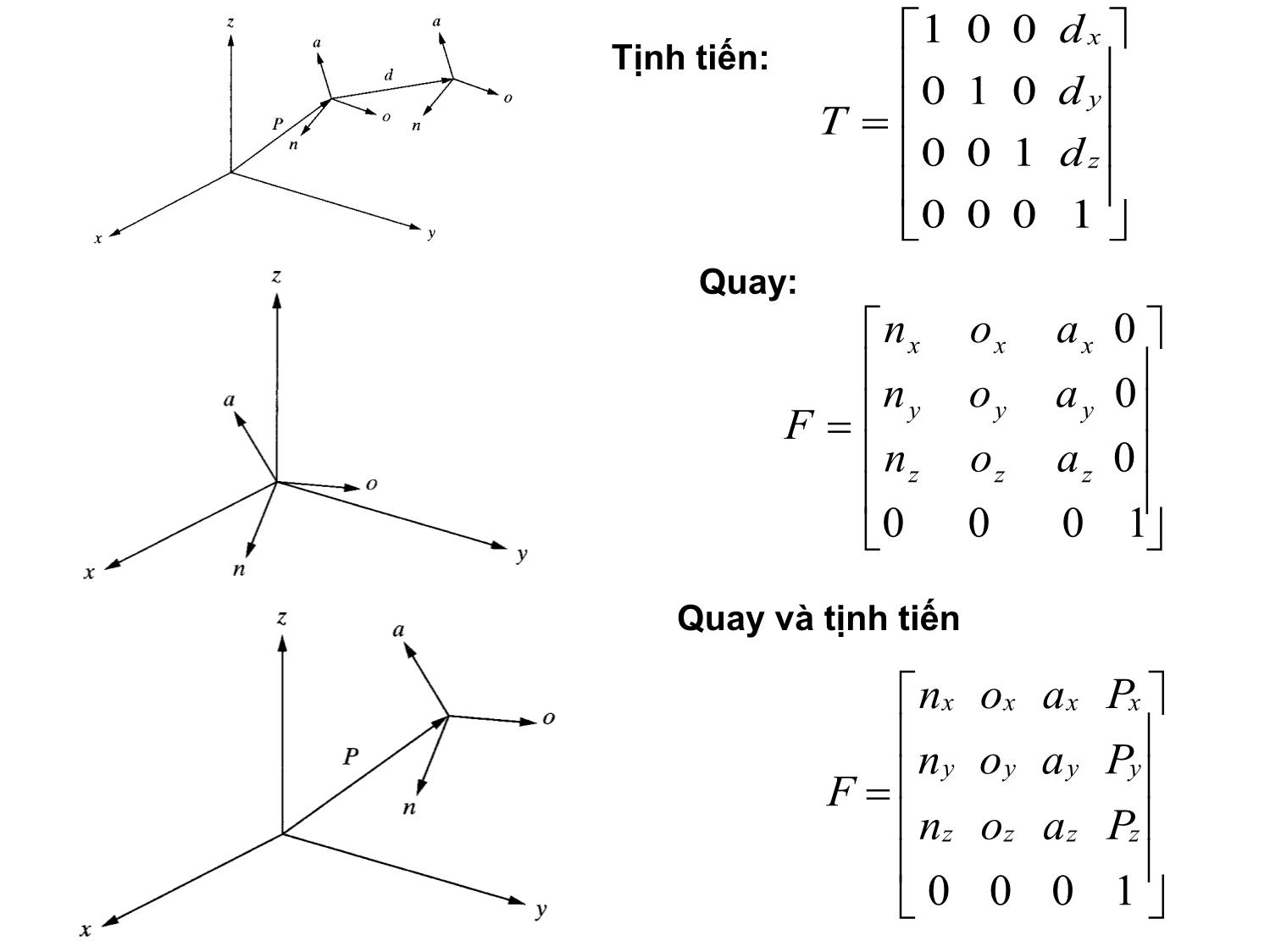
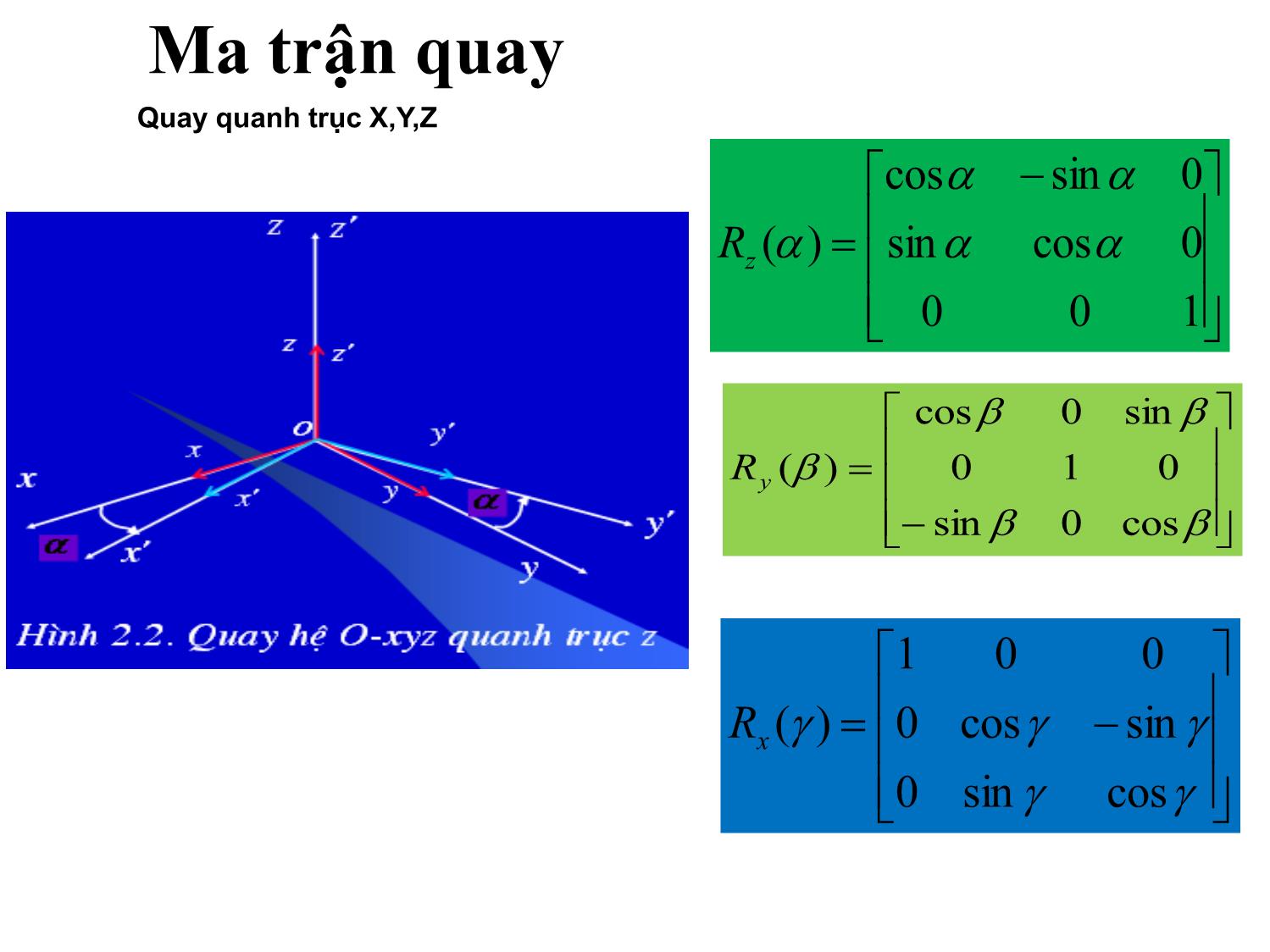
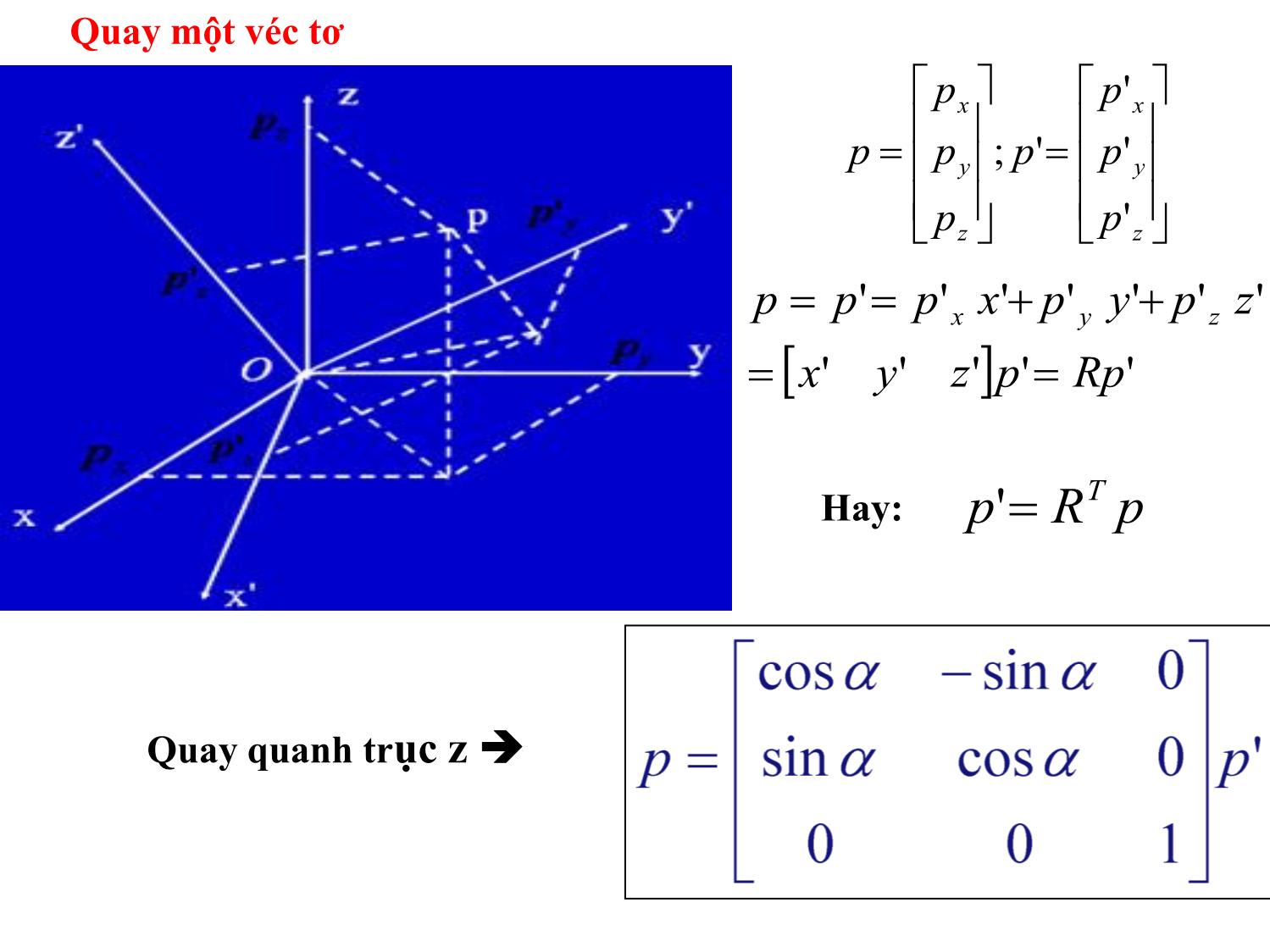
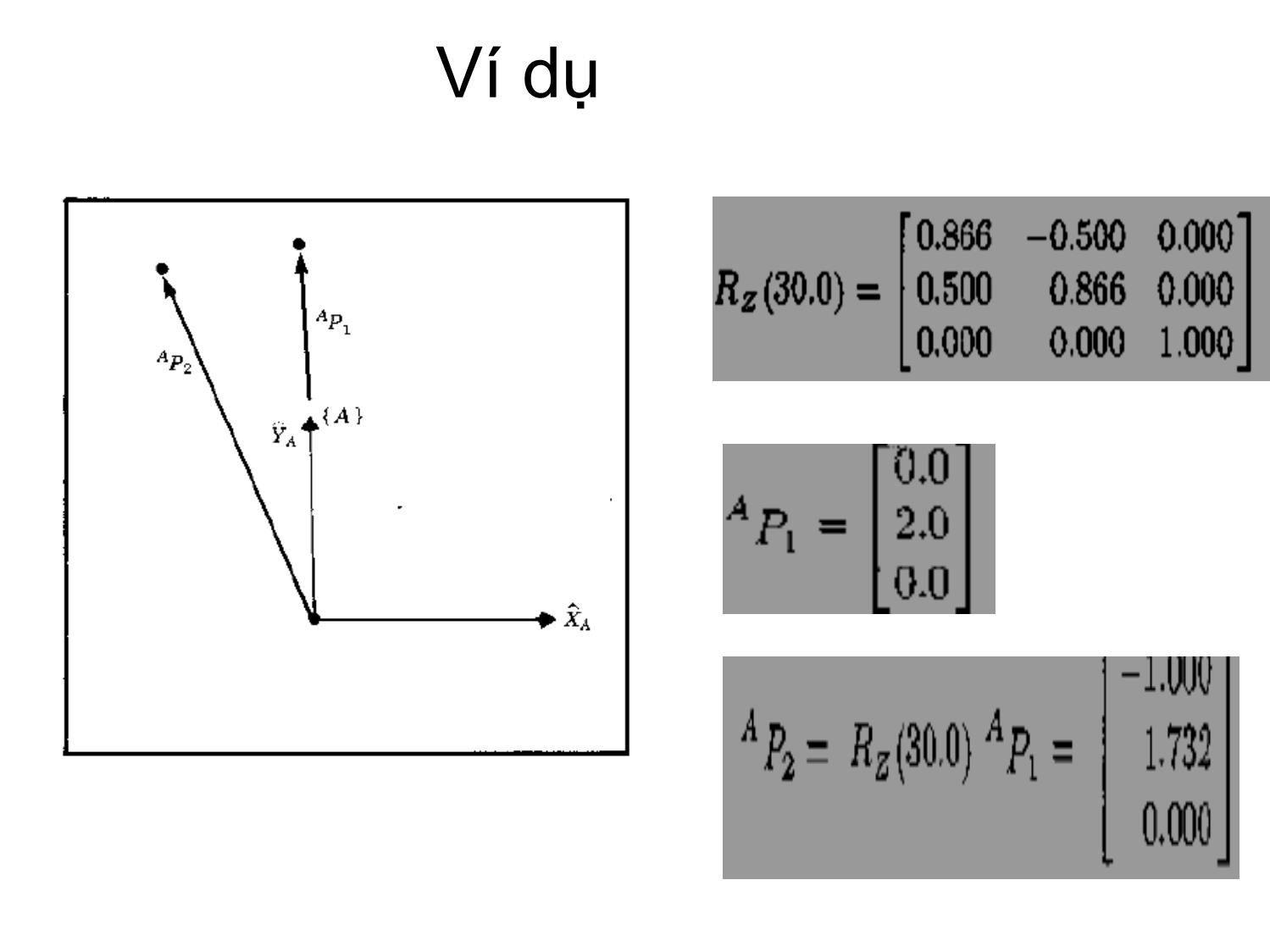
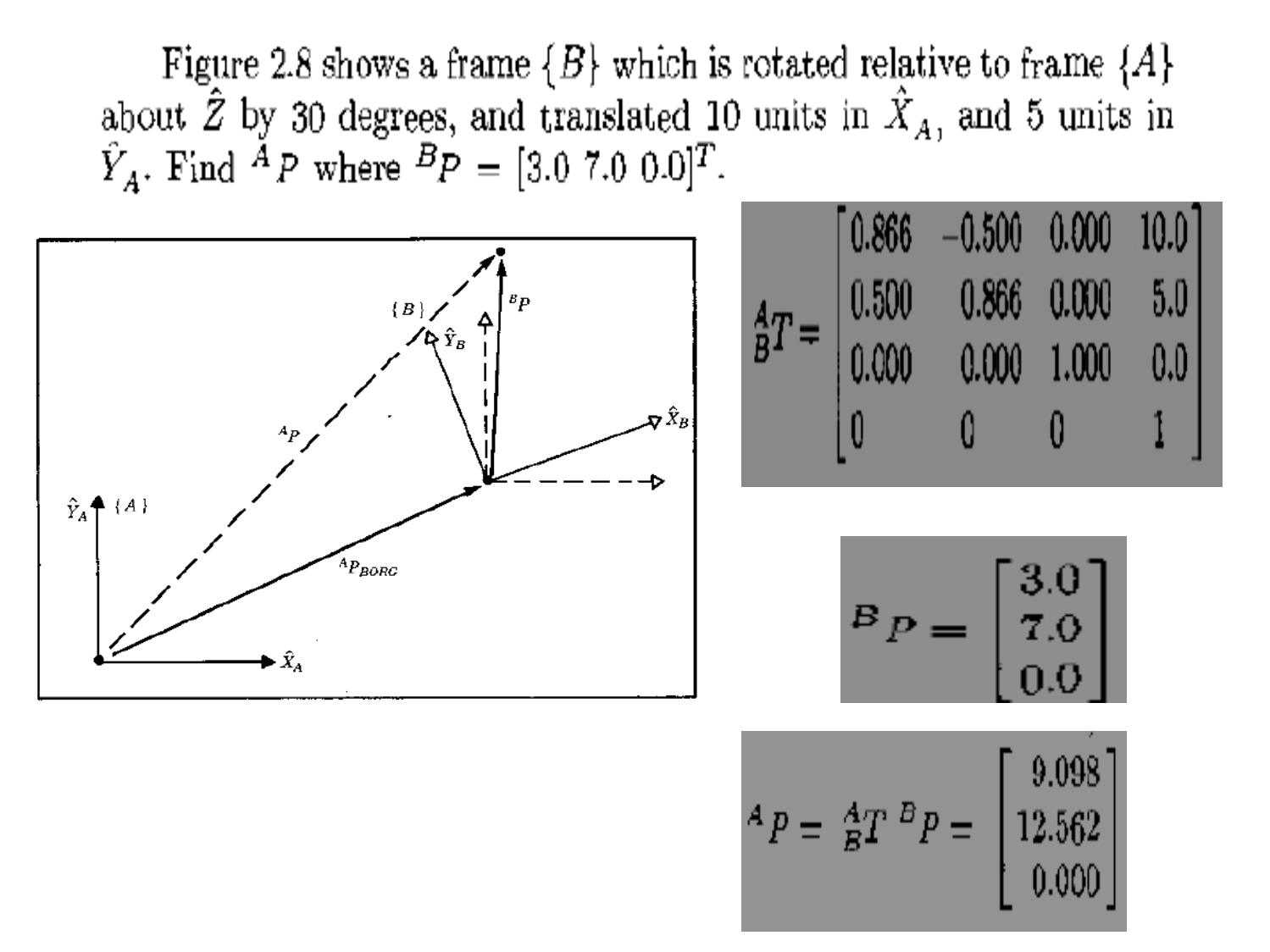
CHƯƠNG 3 : CÁC PHÉP BIẾN ĐỔI TỌA ĐỘ GV: Th.S Nguyễn Tấn Phúc. Tel: 01267102772. Email: phucpfiev1@gmail.com ĐỘNG HỌC ROBOT Hệ tọa độ vật: 2.1. Vị trí và hướng của vật rắn trong không gian Biểu diễn ma trận ^^^__ kcjbiaP zyx w z y x P __ w z c w y b w x a zyx ;; 1000 0 0 0 zzz yyy xxx aon aon aon F 1000 zzzz yyyy xxxx Paon Paon Paon F Quay: Quay và tịnh tiến 1000 100 010 001 z y x d d d T Tịnh tiến: zoyoxoO zyx '''' Hệ tọa độ gốc: Oyxz với các véc tơ đơn vị là x, y, z Vị trí và định hướng của của vật rắn trong không gian gắn lên hệ quy chiếu địa phương O’x’y’z’ z y x o o o o ' ' ' ' Hướng của vật <== các véc tơ đơn vị x’, y’, z’: zzyzxzz zyyyxyy zxyxxxx zyx zyx zyx ''' ''' ''' ' ' ' Các thành phần của các véc tơ đơn vị (x’x, x’y, x’z) là cosin chỉ phương của các trục của hệ tọa độ địa phương so với hệ quy chiếu chung. X’x = X’.cos(X’,X), zzz yyy xxx zyx zyx zyx zyxR ''' ''' ''' ''' Ma trận quay Quay quanh trục X,Y,Z cos0sin 010 sin0cos )(yR 100 0cossin 0sincos )( zR cossin0 sincos0 001 )(xR Quay một véc tơ z y x z y x p p p p p p p p ' ' ' '; ''''' ''''''' Rppzyx zpypxppp zyx pRp T 'Hay: Quay quanh trục z Ví dụ MA TRẬN THUẦN NHẤT Ý NGHĨA MA TRẬN QUAY Xét một phép quay quanh trục X 30, quay quanh trục Z 30. Lưu ý : Trình tự quay theo các trục . GÓC ROLL-PITCH-YAW (RPY) PHÉP QUAY QUANH TRỤC BẤT KỲ Trục có vector đơn vị: r(rx ,ry , rz) , phép quay quanh trục này một góc υ , ma trận quay lúc đó là: MỘT SỐ BÀI TẬP ÁP DỤNG CHUYỂN ĐỔI TỌA ĐỘ THE END OF CHAPTER 3.
File đính kèm:
 bai_giang_co_so_ky_thuat_robot_chuong_3_cac_phep_bien_doi_to.pdf
bai_giang_co_so_ky_thuat_robot_chuong_3_cac_phep_bien_doi_to.pdf

