A prediction model of road traffic fatalities in Ha Noi using improved grey model GM (1,1)

INTERNATIONAL COOPERATION ISSUE OF TRANSPORTATION - Especial Issue - No. 10 43 
I. INTRODUCTION 
With the rapid development of urbanization and motorization across Hanoi, as well as other 
cities in Vietnam, road transportation system is playing an increasingly role in urban 
transportation system. However, the occurrence of road traffic accidents (RTAs) in Hanoi still 
remain high as a result of the speedy growing of motorized vehicles, and it has become a more 
and more important factor that restrict the development of economy and threaten the safety of 
human and public health. According to statistic data, about 7.4 percent of RTAs and 7.1 percent 
of total fatalities by RTAs in Vietnam have occurred in Hanoi [1], and the rate of the road traffic 
fatalities (RTFs) is approximately 8 deaths per 100,000 inhabitants [2]. Accurate forecasting of 
RTAs would greatly contribute to reasonable road networks planning and the improvement 
management of road traffic safety [3], especially in Vietnam where RTAs remain high. So far, 
there are many prediction models of RTAs that have been announced, such as regression 
models, grey models [4-6], artificial neural network [7], hybrid models [8], and so forth. Among 
them, grey prediction models, which are one of most important parts of the grey system theory, 
propounded by Deng [9], have been commonly used in the time series prediction due to their 
A PREDICTION MODEL OF ROAD TRAFFIC FATALITIES IN HANOI 
USING IMPROVED GREY MODEL GM (1,1) 
VUONG XUAN CAN1,2, MOU RUI-FANG1, VU TRONG THUAT2 
1School of Transportation and Logistics, Southwest Jiaotong University, Chengdu,China 
2University of Transport and Communications, No 3 Cau Giay Street, Hanoi, Vietnam. 
Corresponding author’s email:1323972686@qq.com 
Abstract: This study improves the first-order and one-variable grey differential equation 
model (abbreviated as GM(1,1) model), which requires only a limited amount of data to 
estimate the behavior of a system with unknown and known information, to predict road traffic 
fatalities (RTFs) in Hanoi in short-term with experimental data of RTFs from 2010 to 2018. 
Firstly, we introduce basic concept of original GM(1,1), and then an improved GM(1,1) model 
is established based on the modification of the errors. Finally, we compare the performance of 
forecasting models to predict RTFs in Hanoi. The results of prediction models show that the 
forecasting accuracy of the improved GM(1,1) model is higher than the original GM(1,1) 
model. Comparison with original GM(1,1) model, mean absolute percentage error (MAPE) of 
the improved GM(1,1) model is considerably decreased from 8.30% to 1.70%. This proves the 
applicability of the improved GM(1,1) model to make a short-term prediction for RTFs in 
Hanoi. 
Keywords: prediction model, grey model GM (1,1), road traffic fatalities 
 Received: 06/04/2020 Accepted: 13/05/2020 Published online: 14/06/2020 
INTERNATIONAL COOPERATION ISSUSE OF TRANSPORTATION - Especial Issue - No.10 
 44 
simplicity and ability to characterize an unknown system with high accuracy and limited data 
[10,11]. 
In Hanoi, as well as other cities in Vietnam, forecasting of RTAs has not respected in both 
short and long term. Besides, the statistics of RTAs are still difficult and exist many 
inadequacies, such as lack of systematization, under-reporting, incompleteness, incorrectness 
and inaccessibility [1,8,12]. There are many data sources but the data is not sufficient, it is 
difficult to apply traditional statistical analysis methods that require data and information large 
enough with many factors considered. Considering the complexity and uncertainty of the 
influencing factors on RTAs, forecasting of RTAs can be regarded as a grey system with 
unknown and known information [6], so forecasting of RTAs in the context of Vietnamese 
transport using by grey prediction models is very appropriate. 
The first-order one-variable grey differential equation model, abbreviate as GM(1, 1) is 
used most widely among various grey models, and has been successfully applied to various 
fields, e.g., forecasting of RTAs [4,5,6]. The GM(1,1) model has many advantages [13], such as 
small amount of data needed, simple modeling process, and easy to learn and use. However, the 
GM (1,1) model is monotonic due to the exponential function of the prediction model, the 
results of the GM (1,1) model sometime may not be satisfactory for the random fluctuation 
series. Recently the GM (1,1) model has been expanded to improve the accuracy and prediction 
ability. 
In this paper, we first introduce basic concept of GM(1,1), and then present an improved 
GM (1,1) model using Fourier series [14,15,16,17]. Finally, we compare the performance of 
forecasting models to predict in Hanoi in short-term. 
II. MAIN CONTENTS 
2.1. GM (1,1) model 
GM (1, 1) grey prediction model is that through the monotone sequence has been given, by 
means of once additive generates a group of new albinism differential equation. The GM(1, 1) 
model has the three main operations: (1) Accumulating Generation Operator (AGO), (2) grey 
modelling, (3) Inverse Accumulating Generation Operator (IAGO), and it is summarized as 
follows [18]. 
Assume that a non-negative original time-series of data 
)0(X with n samples is expressed 
as: 
})(),...,3(),2(),1({ )0()0()0()0()0( nxxxxX = (1) 
where, the superscription (0) of 
)0(X represents the original series; ),(
)0( kx (k =1, 2,, n) is 
the data point at time k , and 4 n . Let a new cumulative 
)1(X be the first-order AGO of 
)0(X , 
whose elements are generated from 
)0(X : 
})(),...,3(),2(),1({ )1()1()1()1()1( nxxxxX = (2) 
INTERNATIONAL COOPERATION ISSUE OF TRANSPORTATION - Especial Issue - No. 10 45 
where 
=
=
k
i
ixkx
1
)0()1( )()( , for k =1, 2,,n. The generated mean sequence
)1(Z of 
)1(X is 
defined as: 
})(),...,3(),2(),1({ )1()1()1()1()1( nzzzzZ = (3) 
where )()1( kz is the mean value of adjacent data, and is calculated by: 
2),1(5.0)(5.0)( )1()1()1( −+= kkxkxkz (4) 
The GM (1, 1) model can be formed by establishing a first order differential equation for 
)1(X as follows: 
baX
dt
dX
=+ )1(
)1(
 (5) 
where a and b are the developing coefficient and the endogenous control coefficient, 
respectively. They can be calculated by traditional least square method as follows: 
YBBBba TTT ..).(],[ 1−= (6) 
where Y is called data series, B is called data matrix, as follows: 
T)0()0()0( ])(),...,3(),2([ nxxxY = (7) 
−
−
−
=
1)(
......
1)3(
1)2(
)1(
)1(
)1(
nz
z
z
B (8) 
According to Eq. (5), the solution of
)1(X as follows: 
=
 + 
−=+ −
)1()1(ˆ
1,)1()1(ˆ
)0()1(
)0()1(
xx
k
a
b
e
a
b
xkx ak
 (9) 
Applying the IAGO, the forecasted value can be obtained as follows: 
=
 +=+
)1()1(ˆ
1),(ˆ-)1(ˆ)1(ˆ
)0()0(
)1()1()0(
xx
kkxkxkx
 (10) 
or 
=
−−=+ −
)1()1(ˆ
1,)1()1()1(ˆ
)0()0(
)0()0(
xx
ke
a
b
xekx aka
 (11) 
2.2. Improved GM (1,1) model 
In order to improve the accuracy of forecasting models, this study uses Fourier series in 
modifying the errors in the GM(1,1) model [14,15,16,17]. The improved model is implemented 
as follows. 
INTERNATIONAL COOPERATION ISSUSE OF TRANSPORTATION - Especial Issue - No.10 
 46 
Suppose that })(),...,3(),2({ )0()0()0()0( n = is the error sequence of
)0(X where
)(ˆ)()( )0()0()0( kxkxk −= . If all errors are positive, then a remnant GM(1,1) model can be 
built [19]. When the errors can be positive or negative, the errors can be expressed using by 
Fourier series, and are rewritten as follows [14]. 
nkk
n
i
bk
n
i
aak
z
ii ,...,3,2,
1
2
sin
1
2
cos
2
1
)(ˆ
1
0
)0( = 
−
+ 
−
+ 
 (12) 
where 1]2/)1[( −−= nz is called the minimum deployment frequency of Fourier series [15], 
and it only take integer number. Therefore, Equation (12) can be estimated as: 
 PC)0( (13) 
where C is a vector of coefficients; P is a matrix. They can be expressed as 
−

−

−

−

−

−

−

−

−

−

−

−

=
)
1
2
sin()
1
2
cos(...)
1
12
sin()
1
12
cos(
2
1
..................
)
1
2
3sin()
1
2
3cos(...)
1
12
3sin()
1
12
3cos(
2
1
)
1
2
2sin()
1
2
2cos(...)
1
12
2sin()
1
12
2cos(
2
1
n
z
n
n
z
n
n
n
n
n
n
z
n
z
nn
n
z
n
z
nn
P
 (14) 
T
zz bababaaC ],,...,,,,,[ 22110= (15) 
The parameters zz bababaa ,,...,,,,, 22110 are obtained by using the ordinary least squares 
method whose results are in the following equation: 
TTT PPPC )0(1)( −= (16) 
From the original prediction series (
)0(xˆ ) and the error ( )0(ˆ ), prediction series of the 
improved grey model using Fourier series (
)0(
ˆ
Fx ) is determined by 
=
 +=
)1(ˆ)1(ˆ
2),(ˆ)(ˆ)(ˆ
)0()0(
)0()0()0(
xx
kkkxkx
F
F  (17) 
In order to evaluate the performance of the proposed model, we use mean absolute 
percentage error (MAPE), which are defined as follows: 

=
−
=
n
k kx
kxkx
n
MAPE
1
)0(
)0()0(
)(
)(ˆ)(1
 (18) 
where, )(
)0( kx and )(ˆ
)0( kx are the actual value and forecasted value, respectively. The MAPE 
value is more than 10%, the result is an inaccurate forecast, 5%–10% is a reasonable forecast, 
1%–5% is a good forecast, and less than 1% is an excellent forecast [8]. 
INTERNATIONAL COOPERATION ISSUE OF TRANSPORTATION - Especial Issue - No. 10 47 
2.3. APPLICATION OF THE MODELS 
RTFs data of Hanoi from 2010 to 2018 collected from Hanoi Department of Transport 
(HDOT) [20] is selected to establish prediction models. Number of RTFs from 2010 to 2015 is 
used as the in-sample, and number of RTFs from 2016 to 2018 is used as out-of-sample. As 
shown in Table 1, although the trend of RTFs in Hanoi from 2010 to 2018 has decreased 
slightly. 
Table 1. RTFs data of Hanoi from 2010 to 2018. 
Year RTFs Year RTFs Year RTFs 
2010 807 2013 626 2016 594 
2011 749 2014 609 2017 583 
2012 619 2015 602 2018 543 
The actual values and forecasted values implemented by PYHTON 3.8 are shown in Table 
2 to compare relative errors of the models. MAEPs for the different stage are shown in Table 3. 
Table 2. Models values and prediction errors of RTFs in Hanoi. 
Stage Year 
Actual 
value 
Original GM(1,1) Improved GM(1,1) 
Model 
value 
Error 
(%) 
Model 
value 
Error 
(%) 
2010-2015 
2010 807 807 0 807 0 
2011 749 705 -5.85 739 -1.30 
2012 619 671 8.47 629 1.57 
2013 626 639 2.12 616 -1.55 
2014 609 609 -0.06 619 1.59 
2015 602 579 -3.74 592 -1.61 
2016-2018 
2016 594 552 -7.12 604 1.63 
2017 583 525 -9.90 573 -1.67 
2018 543 500 -7.89 553 1.79 
Table 3. MAPEs for the different prediction models. 
Stage 
MAPE (%) Performance 
Original 
GM(1,1) 
Improved 
GM(1,1) 
Original 
GM(1,1) 
Improved 
GM(1,1) 
2010-2015 3.37 1.27 Good Good 
2016-2018 8.30 1.70 Reasonable Good 
Table 2 shows that the improved GM(1,1) model is smaller than the original GM(1,1) 
model by comparing the relative error. As shown in Table 3, it can be seen that MAPE of the 
improved GM(1,1) model and original GM(1,1) from 2016 to 2018 are 8.3% and 1.7%, 
respectively. In comparison with original GM(1,1), MAPE of the improved GM(1,1) is 
considerably decreased. The effectiveness and accuracy of improved GM(1,1) model is higher 
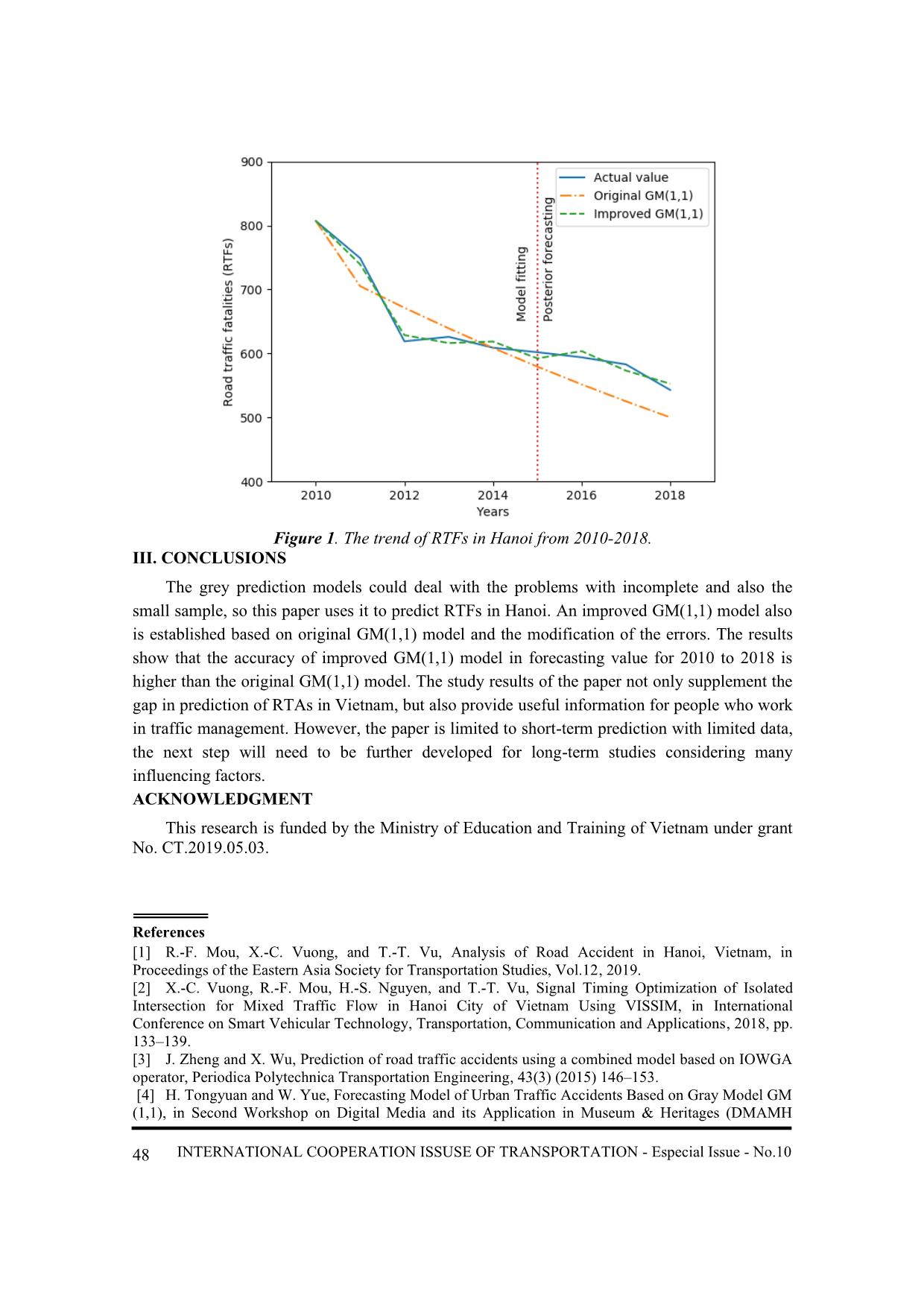
than the original GM(1,1). The trend of RTFs in Hanoi from 2010-2018 by actual values and 
models values is shown in Figure 1. This figure also shows that the improved GM(1,1) model 
has the better forecasting precision in 2016-2018, it is more suitable to make a short-term 
prediction. 
INTERNATIONAL COOPERATION ISSUSE OF TRANSPORTATION - Especial Issue - No.10 
 48 
Figure 1. The trend of RTFs in Hanoi from 2010-2018. 
III. CONCLUSIONS 
The grey prediction models could deal with the problems with incomplete and also the 
small sample, so this paper uses it to predict RTFs in Hanoi. An improved GM(1,1) model also 
is established based on original GM(1,1) model and the modification of the errors. The results 
show that the accuracy of improved GM(1,1) model in forecasting value for 2010 to 2018 is 
higher than the original GM(1,1) model. The study results of the paper not only supplement the 
gap in prediction of RTAs in Vietnam, but also provide useful information for people who work 
in traffic management. However, the paper is limited to short-term prediction with limited data, 
the next step will need to be further developed for long-term studies considering many 
influencing factors. 
ACKNOWLEDGMENT 
This research is funded by the Ministry of Education and Training of Vietnam under grant 
No. CT.2019.05.03. 
References 
[1] R.-F. Mou, X.-C. Vuong, and T.-T. Vu, Analysis of Road Accident in Hanoi, Vietnam, in 
Proceedings of the Eastern Asia Society for Transportation Studies, Vol.12, 2019. 
[2] X.-C. Vuong, R.-F. Mou, H.-S. Nguyen, and T.-T. Vu, Signal Timing Optimization of Isolated 
Intersection for Mixed Traffic Flow in Hanoi City of Vietnam Using VISSIM, in International 
Conference on Smart Vehicular Technology, Transportation, Communication and Applications, 2018, pp. 
133–139. 
[3] J. Zheng and X. Wu, Prediction of road traffic accidents using a combined model based on IOWGA 
operator, Periodica Polytechnica Transportation Engineering, 43(3) (2015) 146–153. 
 [4] H. Tongyuan and W. Yue, Forecasting Model of Urban Traffic Accidents Based on Gray Model GM 
(1,1), in Second Workshop on Digital Media and its Application in Museum & Heritages (DMAMH 
INTERNATIONAL COOPERATION ISSUE OF TRANSPORTATION - Especial Issue - No. 10 49 
2007), 2007, pp. 438–441. 
[5] U. Becker and H. Manz, Grey systems theory time series prediction applied to road traffic safety in 
Germany, IFAC-PapersOnLine, 49 (3) (2016) 231–236. 
[6] A. Mohammadi, L. Moradi, A. Talebnejad, and A. Nadaf, The use of grey system theory in 
predicting the road traffic accident in Fars province in Iran, Aust. J. Bus. Manag. Res., 1(9)(2011) 18-23. 
[7] A. P. Akgüngör and E. Doğan, An artificial intelligent approach to traffic accident estimation: 
Model development and application, Transport, 24(2)(2009)135–142. 
 [8] X.-C. Vuong, R.-F. Mou, and T.-T. Vu, Analysis and Forecast of Road Traffic Accidents in Vietnam 
Based on Grey BP Neural Network, in The 11th National Conference on Fundamental and Applied IT 
Research, 2018, pp. 35–41. 
[9] D. Julong, Introduction to grey system theory, J. grey Syst., 1(1)(1989) 1–24. 
[10] L. Qu, D. He, and R. Jia, Optimized grey model based on cuckoo search algorithm and its prediction 
application, J. Inf. &COMPUTATIONAL Sci., 11(5)(2014) 1419–1426. 
[11] S. Liu, J. Forrest, and Y. Yang, A brief introduction to grey systems theory,in Proceedings of 2011 
IEEE International Conference on Grey Systems and Intelligent Services, 2011, pp. 1–9. 
[12] N. H. Duc, D. T. M. Hoa, N. T. Huong, and N. N. Bao, Study on quality of existing traffic accident 
data in Vietnam, in Proceedings of the Eastern Asia Society for Transportation Studies, 2011, vol. 8. 
[13] B. Zeng, H. Duan, Y. Bai, and W. Meng, Forecasting the output of shale gas in China using an 
unbiased grey model and weakening buffer operator, Energy, 151(2018) 238–249. 
[14] C. L. Tan and S. P. Chang, Residual correction method of Fourier series to GM (1, 1) model, in 
Proceedings of the first national conference on grey theory and applications, Kauhsiung, Taiwan, 1996, 
pp. 93–101. 
[15] Y.-L. Huang and Y.-H. Lee, Accurately forecasting model for the stochastic volatility data in 
tourism demand, Mod. Econ., 2(05)(2011) 823-829. 
[16] Z. Guo, X. Song, and J. Ye, A Verhulst model on time series error corrected for port throughput 
forecasting, J. East. Asia Soc. Transp. Stud., 6(2005) 881–891. 
[17] W. Chia-Nan and P. Van-Thanh, An improved nonlinear grey Bernoulli model combined with 
Fourier series,” Math. Probl. Eng., (2015) No.740272. 
[18] J. L. Deng, Grey forecasting and decision, Huazhong Univ. Sci. Technol. Press. Wuhan, pp. 97–134, 
1986. 
[19] S. Liu and J. Y. L. Forrest, Grey systems: theory and applications. Springer Science & Business 
Media, 2010. 
[20] HDOT, Traffic Safety Annual Reports (2010-2018), Hanoi, Vietnam, 2018.