Xây dựng mô hình con lắc ngược dạng quay trên Simulink của Matlab

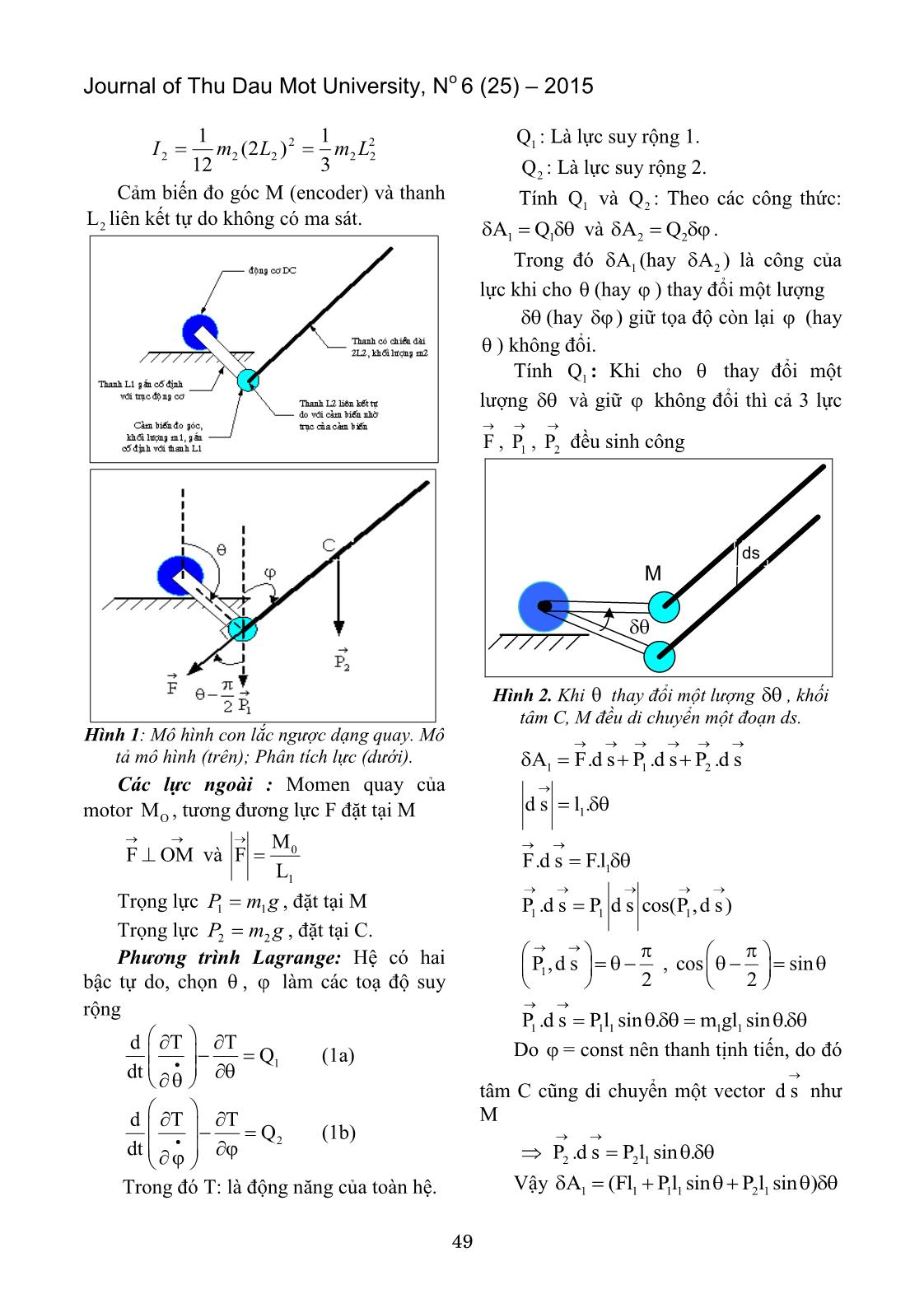
Tạp chí Đại học Thủ Dầu Một, số 6 (25) – 2015 
 48 
XÂY DỰNG MÔ HÌNH CON LẮC NGƯỢC DẠNG 
QUAY TRÊN SIMULINK CỦA MATLAB 
Nguyễn Văn Sơn 
T M TẮT 
 . 
  T 
 mà 
 trong 
 . 
Đối tượng con lắc ngược nói chung và 
con lắc ngược dạng quay nói riêng là các 
đối tượng có tính bất ổn định cao, do đó 
thường được sử dụng để kiểm nghiệm các 
thuật toán điều khiển. Trong điều kiện chưa 
thể xây dựng mô hình điều khiển thực hoặc 
trước khi xây dựng mô hình điều khiển 
thực thì mô hình ảo với thuật toán điều 
khiển trên Simulink của MATLAB là hợp 
lý vì các lý do: thuận lợi, hiệu quả và ít tốn 
kém. Bài báo này giới thiệu các bước xây 
dựng mô hình con lắc ngược trên Simulink 
của MATLAB và thuật toán điều khiển con 
lắc ngược b ng giải thuật fuzzy như là m t 
ví dụ về giải thuật điều khiển. Với các công 
cụ được tạo ra là mô hình con lắc ngược và 
các thuật giải điều khiển có thể được sử 
dụng là bài thực tập cho môn h c điều 
khiển tự đ ng 
 1. y ng h nh n ắ ng 
 ng u y 
 Hệ con lắc ngược được mô tả trên hình 
(1) gồm các phần tử: 
 – Đ ng c . 
 – Hai thanh: thanh ngắn và thanh dài, 
thanh ngắn m t đầu liên kết chặt với đầu 
trục của motor, thanh dài m t đầu liên kết 
tự do với thanh ngắn thông qua cảm biến 
đo góc đặt ở đầu còn lại của thanh ngắn 
 – Hai cảm biến đo góc: Cảm biến đo 
góc  đặt ở đầu trục của đ ng c , cảm biến 
đo góc đặt ở đầu cuối thanh ngắn, như 
đ nói ở trên (hình 1). 
 Đ ng c có momen quán tính Io đối 
với trục quay O, chịu momen quay Mo 
 Cảm biến đo góc (M) để đo góc giữa 
thanh L1 và thanh L2 đặt cuối thanh L1,có 
khối lượng 1m , 1OM L , momen quán 
tính đối với trục quay O là 2111 LmI . 
Thanh 1L có khối lượng không đáng kể so 
với cảm biến đo góc M 
 Thanh L2 có khối tâm C, chiều dài 
2L2, khối lượng 2m , momen quán tính đối 
với C là: 
Journal of Thu Dau Mot University, No 6 (25) – 2015 
 49 
2
22
2
222
3
1
)2(
12
1
LmLmI 
 Cảm biến đo góc M (encoder) và thanh 
2L liên kết tự do không có ma sát 
Hình 1 Mô 
 (trên); ( ớ ). 
 Các lực ngoài Momen quay của 
motor OM , tư ng đư ng lực đặt tại M 
 F OM
 và 0
1
M
F
L
Tr ng lực gmP 11 , đặt tại M 
Tr ng lực gmP 22 , đặt tại C 
 P ương trìn L gr nge Hệ có hai 
bậc tự do, ch n  , làm các toạ đ suy 
r ng 
 1
d T T
Q
dt
  
  
 (1a) 
 2
d T T
Q
dt
   
  
 (1b) 
 Trong đó T: là đ ng năng của toàn hệ 
1Q : Là lực suy r ng 1. 
 2Q : Là lực suy r ng 2. 
 Tính 1Q và 2Q : Theo các công th c: 
1 1A Q  và 2 2A Q  . 
Trong đó 1A (hay 2A ) là công của 
lực khi cho  (hay ) thay đổi m t lượng 
  (hay  ) giữ t a đ còn lại (hay 
 ) không đổi 
 Tính 
1Q : Khi cho  thay đổi m t 
lượng  và giữ không đổi thì cả 3 lực 
F
, 
1P
, 
2P
 đều sinh công 
M
ds

 ìn 2. Khi   
 1 1 2A F.d s P .d s P .d s
 
1d s l .
  
1F.d s F.l
  
1 1 1P .d s P d s cos(P ,d s)
1P ,d s
2
  
 , cos sin
2
  
 1 1 1 1 1P .d s Pl sin . m gl sin .
   
Do const nên thanh tịnh tiến, do đó 
tâm C c ng di chuyển m t vector d s
 như 
M 
 2 2 1P .d s P l sin .
  
Vậy 1 1 1 1 2 1A (Fl Pl sin P l sin )    
Tạp chí Đại học Thủ Dầu Một, số 6 (25) – 2015 
 50 
 1 1A Q  
 1 1 1 1 2 1Q Fl Pl sin P l sin   
 Tính 2Q : Cho thay đổi m t lượng 
 , giữ  không đổi, khi đó ch có 2P sinh 
công 
2 2 2 2A P .d s P ds cos P ,d s
 
2ds l
  
2P ,d s
2
 , cos sin
2
 ìn 3. Khi  
2 2 2A P l sin .  
2 2A Q .d 
Vậy 1 1 1 1 2 1Q Fl Pl sin P l sin   (2a) 
Và 2 2 2Q P l sin (2b) 
Tính đ ng năng của hệ: 0 1 2T T T T 
0T : đ ng năng của motor, 
2
0 0
1
T I
2
  
1T : đ ng năng của sensor đo góc M, 
2
1 1
1
T I
2
 
2
2
1 1
1
m l
2
  
2T : đ ng năng của thanh 2l , 
2
2
2 2 C 2
1 1
T m V I
2 2
Biểu th c trên cho thấy đ ng năng 2T 
đ ng năng tịnh tiến của khối tâm C 
( 2
2 C
1
m V
2
) đ ng năng quay quanh C 
(
2
2
1
I
2
 ). 
CV OC OM MC
2 2
2
CV OM MC 2 OM MC cos OM,MC
2 2 2
2
1 1OM l l
   
2 2 2
2
2 2MC l l
 t góc OM,MC
 Khi 
0
0
 
 hay 
0
0
 
 , ( )  
 Khi 
0
0
 
 hay 
0
0
 
 , 
( )  
Do đó trong m i trường hợp 
1 22 OM MC cos 2l l cos
  
1 22l l cos( )
   
Vậy 
2 2
2 2 2
2 C 2 1 2 1 2
1 1
m V m l l 2l l cos( )
2 2
    
Đ ng năng quay quanh C: 
2 22
2
2 2
l1 1
I (m )
2 2 3
2
2
2 2
1
m l
6
 đ ng năng toàn phần T 
Journal of Thu Dau Mot University, No 6 (25) – 2015 
 51 
2 2 2 2 2 2 2
2 2 2 2
0 1 1 2 1 2 2 2 1 2 2 2
1 1 1 1 1
T I m l m l m l m l l cos( ) m l
2 2 2 2 6
      
2 2 2 2
2 2 2
0 1 1 2 1 2 2 2 1 2
1 2
T I m l m l m l m l l cos( )
2 3
    (3) 
 Tính 
T

 
, 
T

, 
T

 
 và 
T
 
 để thay vào biểu th c (1a) và (1b) 
 2 2
0 1 1 2 1 2 1 2
T
I m l m l m l l cos( )

   

 (4a) 
2 1 2
T
m l l sin( )
 
   

 (4b) 
 2
2 2 2 1 2
T 4
m l m l l cos( )
3

  
 
 (4c) 
2 1 2
T
m l l sin( )
 
   
 
 (4d) 
 2 20